基于任務剖面的導彈LRU備件規劃方法

洪東跑，許 諾，金 晶，張海瑞

（中國運載火箭技術研究院，北京100076）

基于任務剖面的導彈LRU備件規劃方法

洪東跑，許 諾，金 晶，張海瑞

（中國運載火箭技術研究院，北京100076）

研究了不同環境條件對導彈產品壽命的影響，利用Poisson過程來描述導彈現場可更換單元（line replaceable unit，LRU）在全壽命周期中的維修情況，給出了一種基于任務剖面的導彈LRU備件規劃方法。通過對全壽命周期任務剖面進行分析，綜合考慮不同典型任務剖面對LRU可靠性的影響，利用Poisson過程建立LRU備件量模型。通過考慮LRU備件貯存失效和定期檢測損耗，對備件量模型進行了修正。結合實例表明，該方法在導彈貯存壽命剖面下對LRU備件量進行了合理規劃，確保導彈滿足戰備完好性要求，并節約了全壽命周期費用。

導彈；環境條件；現場可更換單元；備件；任務剖面

0 引 言

隨著高新技術的引進，裝備的任務剖面和使用環境條件日益復雜，基于裝備任務需求和系統效能的實戰要求不斷深化，裝備綜合保障正由傳統的“規模型”逐步向“精確化”發展［1］。綜合保障成為影響導彈武器系統戰備完好性、任務成功性和全壽命周期費用的重要因素。備件規劃作為綜合保障的一項重要工作之一，對導彈武器系統的戰備完好性和全壽命周期費用有重要的影響［23］。在滿足戰備完好性的前提下，準確規劃備件量，并合理地權衡費用成為了裝備綜合保障領域的一個研究熱點［46］。目前，關于裝備備件量要求，大多針對馬爾可夫系統，利用有限狀態的齊次馬爾可夫過程理論給出_備件量的解析表達式［710］，但大多數研究是從戰備完好性和費用角度出發，而忽視了裝備在全壽命周期中經歷的不同任務剖面對備件量的影響［11-13］。對于導彈武器系統，其備件規劃受裝備數量、維修策略、戰備完好性、可靠性水平和費用等影響［14］，而導彈裝備數量、維修策略通常都是確定在滿足戰備完好率和盡量節約全壽命周期費用約束下，可靠性水平就成為了決定其備件量的主要因素。在全壽命周期中，導彈系統的環境、功能、狀態及演化過程均包含有隨機的特性，故其可靠性特征具有時間上的動態特性、環境上的差異特性、層次上的變化特性及對象上的關聯特性。環境上的差異特性是系統的一個重要特性，在不同環境條件下，其可靠性會表現出不同的水平［15］。如忽略環境條件對可靠性的影響，則備件規劃的結果往往會有較大的偏差，影響了導彈的戰備完好性，并最終會增加產品的全壽命周期費用。

為此，本文針對導彈綜合保障發展需求，對導彈全壽命周期任務剖面進行分析，研究了全壽命剖面內環境條件對導彈的影響，利用Poisson過程來描述導彈現場可更換單元（line replaceable unit，LRU）在貯存過程中的更換情況，給出了一種基于任務剖面的導彈LRU備件規劃方法。

1 環境條件對導彈影響分析

環境條件是指產品在任務剖面內所經受到的周圍空間與隨時間變化的各種物理、化學和生物的激勵力的狀態。任務剖面是指產品在完成規定任務這段時間內所經歷的事件和環境的時序描述。對于導彈產品，在生產交付后到執行作戰任務或退役之前，通常要經歷接裝、運輸、轉載、戰備值班、戰備轉級、測試、保養、維修等任務剖面。以某導彈為例，其在交付之后的典型任務剖面如圖1所示。

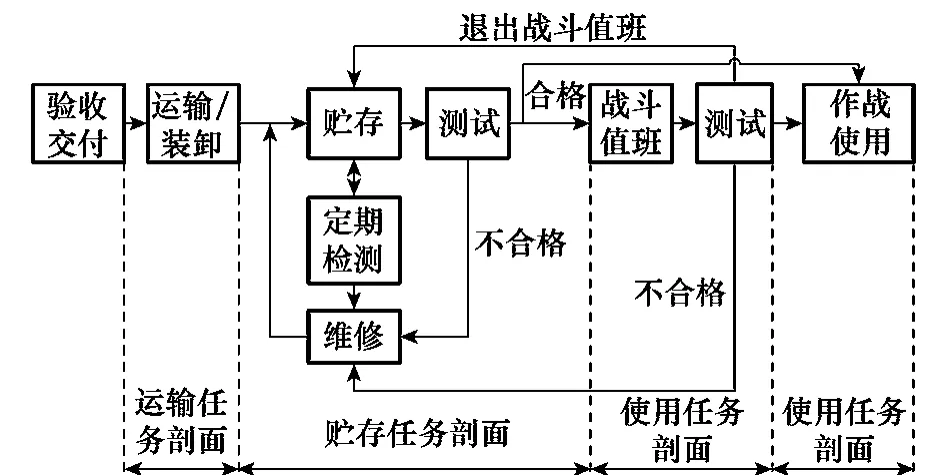
圖1 某導彈典型任務剖面

對導彈在全壽命周期內的任務剖面進行分析，假設存在n種典型任務剖面，記為M1，M2，…，Mn。對于不同的任務剖面內，其對應的環境剖面也不一致，而產品的可靠性受環境條件影響較大，在不同的環境下會表現不同的可靠性水平。故在不同任務剖面下，產品的可靠性水平也存在較大差異，記剖面Mi所對應的失效率為λi（i＝1，2，…，n）。通過對全壽命周期內各種典型任務剖面所經歷的時間進行統計分析，記剖面Mi所經歷的時間占整個壽命時間的比例為ηi（i＝1，2，…，n）。綜合考慮不同任務剖面對產品可靠性的影響，可得產品在全壽命周期內的平均失效率為

在工程實踐中，通常難以確定產品在所有典型任務剖面下的失效率，但一般比較容易確定產品在貯存任務剖面下的失效率，記為λ0。由于不同任務剖面下的環境條件不同，通常可利用環境折合系數（或稱環境因子）來描述不同環境條件下的壽命等價折合關系，在加速壽命試驗中又稱為加速系數［16］。由于環境折合的目的是對產品進行可靠性分析，故可認為環境折合的準則是可靠性不變，即產品在某一環境下經歷一定壽命的可靠性應該與另一環境下經歷折合后對應壽命的可靠性一致［17］。假設產品在環境Ⅰ和環境Ⅱ下壽命分布函數分別為F1（t）和F2（t），其中F1（t）和F2（t）分布類型相同，可得環境Ⅰ對環境Ⅱ的折合系數k滿足

即在環境Ⅰ下的壽命t1相當于在環境Ⅱ下的壽命kt1。利用產品在不同任務剖面下的數據，可以確定折合系數k。記任務剖面Mi對貯存任務剖面的環境折合系數為ki，則有

將ki代入式（1），可得

關于環境折合系數的統計推斷方法，通常利用產品的環境試驗、可靠性試驗和加速試驗等變環境試驗數據，通過統計分析得到環境折合系數的估計［18-20］。由于導彈武器系統在全壽命周期過程中經歷的環境相對復雜，需要分析貯存環境因素對其可靠性的影響，包括溫度、濕度和振動等單項環境因素的影響，以及各環境因素之間交互作用的影響。在此基礎上，利用加速貯存壽命試驗等變環境貯存壽命數據，針對試驗環境條件與實際任務剖面下環境條件的差異性，可通過比例風險模型，綜合利用不同環境下的試驗數據確定環境折合系數［17］，以提高環境折合系數計算精度。在缺乏試驗數據的情況下，環境折合系數的取值可根據工程經驗選取，但應根據試驗數據逐步修正。

2 備件規劃方法

目前，國內外導彈武器系統通常采用基層級、中繼級和基地級三級維修體制。在基層級通常采用換件修理方式對LRU進行維修，因此采用LRU作為備件形式。鑒于導彈武器系統具有長壽命、高可靠的特點，同時導彈LRU的維修時間通常較短，故可不考慮維修時間對備件量的影響。導彈LRU的壽命一般服從指數分布，記為F（t）＝1－exp（－λt）。對于批量為n0的導彈，某LRU在規定時間τ內出現失效時，即可進行維修更換，不考慮維修時間對壽命時間的影響，此過程可以看成是截尾時間為τ的有替換定時截尾試驗，此時某LRU的更換次數X（τ）服從Poisson分布

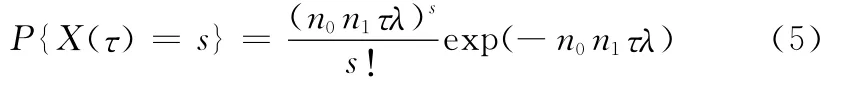
式中，n1為某LRU產品在一發導彈上的裝配量；s為初始備件量。假設在規定時間τ內，某LRU產品既沒有追加新的備件，也沒有修復故障件的加入，則某LRU的更換次數X（τ）滿足

式中，γ為初始備件滿足率，是指在規定的時間周期τ內，現有備件量s可以滿足LRU更換次數需求的概率，它反映了備件保障水平。根據現役導彈武器系統裝備部隊以來多年積累的維修保障經驗，可將LRU分為一般件、易損件和特易損件。對于一般件，初始備件量滿足概率γ較小，一般可取0.85，而對于易損件和特易損件，γ一般可分別取0.9和0.95。

記初始備件量置信下限為sL，sL滿足

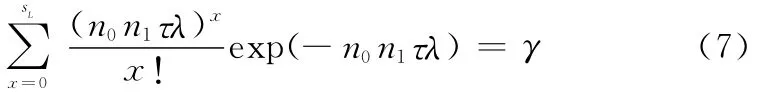
由Γ分布與Poisson分布累積項間的恒等式，可將式（7）表示為不完全Γ函數

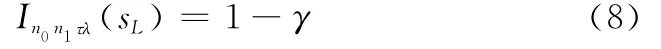
由式（8）可知，LRU的備件量與其失效率、壽命時間、導彈裝備數量、裝配量和置信水平等直接相關。已知各參數n0、n1、τ和γ，將式（4）產品的平均失效率ˉλ代入式（8），可得初始備件量置信下限sL。

在貯存過程中，導彈要定期進行檢測。在定檢過程中，可能對某些LRU造成損壞，需要進行更換。故在計算備件量時，需要考慮貯存過程中消耗的LRU。對于在貯存過程中定期檢測后需要更換的LRU，其年度備件需求數sa滿足

式中，t0為檢測周期；q為定期檢測需要消耗的LRU更換率。

對于可修復的LRU，鑒于LRU的維修需要返回中繼級或基地級，維修周期一般較長。為了簡化計算，不考慮在貯存過程中隨機失效的LRU的可修復性。但由于定期檢測周期一般較長，檢測消耗的LRU有充足的維修時間，修復后可以歸入周轉備件繼續使用，故式（9）備件需求數可變化為

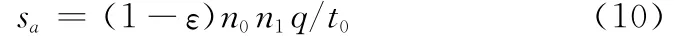
式中，ε為可修復LRU的修復率，對于不可修復的LRU，令ε＝0。

在貯存過程中，受貯存環境因素的影響，備件也可能發生失效。記某LRU的備件失效率為λ0，假設在規定時間τ內，LRU的失效比例（失效數與LRU總數之比）與LRU的失效率滿足線性關系，則LRU備件的失效比例ρ滿足

考慮到備件自身的失效，由式（11）可得LRU備件的總數為

由于備件量為整數，利用式（12）確定備件量時，需要對計算結果進行取整化。在工程應用中，為了便于對不同LRU備件情況進行對比分析，通常還需要確定儲備比例，記備件儲備比例為δ，則有

由式（8）、式（12）和式（13）可以看出，LRU的裝備量和備份量之間并不是線性關系，即儲備比例δ與裝備量n0n1相關。這是因為在裝備數量較大時，相同LRU的備件是可以互換的，儲備比例下降，備份量也相應的減少。因此，在對不同的LRU備件情況進行對比分析時，需要考慮各自的裝備量情況。

3 實 例

某導彈武器系統裝備數量n0＝100，每臺導彈武器系統某LRU的裝配量n1＝1。通過對該導彈武器系統的全壽命周期任務剖面進行分析，確定運輸、庫房存放、測試和戰斗值班為4種典型任務剖面。該LRU在貯存任務剖面下的失效率λ0＝0.008（1／a），在不同任務剖面下的壽命信息如表1所示。

表1 某LRU任務剖面信息

將表1的數據代入式（4），可得該LRU的平均失效率ˉλ＝0.014 4（1／a）。取備件滿足概率γ＝0.9，在定期檢測時不會造成損耗，計算可得該LRU在不同儲備時間t時的備件量和儲備比例，如表2所示。

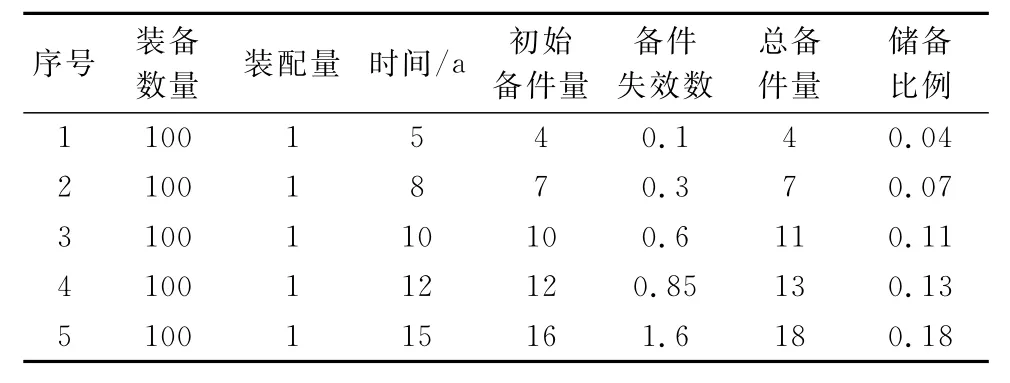
表2 某LRU備件量和儲備比例

通過對表2進行分析可知，在不考慮備件自身貯存失效的情況下，備件量和貯存時間近似滿足線性關系。而在考慮備件自身失效時，備件量隨貯存時間遞增，不再滿足線性關系。在工程應用中，可結合導彈裝備數量、導彈批次生產周期、導彈貯存壽命、備件生產周期和備件費用等諸多因素選擇合理的備件周期（τ）和總備件量。

4 結 論

針對導彈綜合保障發展需求，對導彈全壽命周期任務剖面進行分析，研究了環境條件對導彈可靠性的影響，利用環境折合系數實現不同任務剖面的等價折合，能較好地度量LRU在全壽命周期中的可靠性水平。進而利用Poisson過程來描述導彈LRU的維修情況，建立LRU備件量模型。結合實例表明，該方法綜合考慮了導彈裝備數量、維修策略、備件滿足率、LRU可靠性和備件貯存失效等因素對備件量的影響，有效地提高了備件規劃的合理性。在滿足全壽命周期費用約束下，可顯著地提高導彈戰備完好性。

［1］Liu T H，Zhang Z H，Liang S J，et al.Analytical algorithm of spare demand for Weibull-type repairable system［J］.Systems Engineering and Electronics，2012，34（5）：966- 972.（劉天華，張志華，梁勝杰，等.威布爾型可修備件需求量的解析算法研究［J］.系統工程與電子技術，2012，34（5）：966- 972.）

［2］Zhao J Z，Xu T X，Li H J，et al.Consumption forecast of missile spare parts based on improved Theil coefficient［J］.Systems Engineering and Electronics，2013，35（8）：1681- 1686.（趙建忠，徐廷學，李海軍，等.基于改進Theil不等系數的導彈備件消耗預測［J］.系統工程與電子技術，2013，35（8）：1681- 1686.）

［3］Cheng H L，Kang R，Xiao B P，et al.Spare model under the constraint of spare sufficiency［J］.Systems Engineering and Electronics，2007，29（8）：1314- 1316.（程海龍，康銳，肖波平，等.備件滿足率約束下的備件模型［J］.系統工程與電子技術，2007，29（8）：1314- 1316.）

［4］Nguyen T，Yeung T，Castanier B.Optimal maintenance and replacement decisions under technological change with consideration of spare parts inventories［J］.International Journal of Production Economics，2013，143（2）：472- 477.

［5］Huiskonen J.Maintenance spare parts logistics：special characteristics and strategic choices［J］.International Journal of Production Economics，2001，71：125- 133.

［6］Jaarsveld W，Dekker R.Spare parts stock control for redundant systems using reliability centered maintenance data［J］.Reliability Engineering&System Safety，2011，96（11）：1576- 1586.

［7］Wang N C，Kang R，Cheng H L.Study on the dynamic characteristics of spare inventory based on Markov process［J］.Acta Armamentarii，2009，30（7）：984- 988.（王乃超，康銳，程海龍.基于馬爾可夫過程的備件庫存動態特性分析［J］.兵工學報，2009，30（7）：984- 988.）

［8］Isotupa K.AN（s，S）Markovian inventory system with lost sales and two demand classes［J］.Mathematical and Computer Modeling，2006，43（7／8）：687- 694.

［9］Perez-Ocon R，Montoro-Cazorla D.Transient analysis of a repairable system，using phase-type distributions and geometric processes［J］.IEEE Trans.on Reliability，2004，53（2）：185- 192.

［10］Yanez M，Joglar F，Modarres M.Generalized renewal process for analysis of repairable systems with limited failure experience［J］.Reliability Engineering and System Safety，2002，77（2）：167- 180.

［11］Gu J，Zhang G，Li K W.Efficient aircraft spare parts inventory management under demand uncertainty［J］.Journal of Air Transport Management，2015，42（1）：101- 109.

［12］Barabadi A，Barabady J，Markeset.Application of reliability models with covariates in spare part prediction and optimization—a case study［J］.Reliability Engineering&System Safety，2014，123（1）：1- 7.

［13］Lengu D，Syntetos A A，Babai M Z.Spare parts management：Linking distributional assumptions to demand classification［J］.European Journal of Operational Research，2014，235（3）：624- 635.

［14］Guo L H，Zhang W J，Kang R.Maintenance support modeling and simulating technology for missile weapon system［J］.Acta Armamentarii，2006，27（5）：851- 856.（郭霖瀚，章文晉，康銳.導彈武器系統維修保障建模與仿真［J］.兵工學報，2006，27（5）：851- 856.）

［15］Hong D P，Ma X B，Zhao Y.Integrated reliability assessment based on proportional risk model［J］.Systems Engineering and Electronics，2010，32（10）：2132- 2135.（洪東跑，馬小兵，趙宇.基于比例風險模型的可靠性綜合評估［J］.系統工程與電子技術，2010，32（10）：2132- 2135.）

［16］Essayed E A，Wang H Z.Bayes＆classical estimation of environmental factors for binomial distribution［J］.IEEE Trans.on Reliability，1996，45（4）：661- 665.

［17］Hong D P，Ma X B，Zhao Y，et al.Environment referring factor based on proportional hazards model［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36（4）：443- 446.（洪東跑，馬小兵，趙宇，等.基于比例風險模型的環境折合系數確定方法［J］.北京航空航天大學學報，2010，36（4）：443- 446.）

［18］Li F，Shi Y M，Jing Y.Bayesian estimation for environmental factor of two parameter of Weibull distribution［J］.Systems Engineering and Electronics，2008，30（1）：186- 189.（李鳳，師義民，荊源.兩參數Weibull分布環境因子的Bayes估計［J］.系統工程與電子技術，2008，30（1）：186- 189.）

［19］Wang H Z，Ma B H，Shi J S.Estimation of environmental factor for the log normal distribution［J］.Microelectronics&Reliability，1992，32（5）：679- 685.

［20］Zhou Y Q，Weng Z X，Ye X T.Study on accelerated factor and condition for constant failure mechanism（I）—the case for lifetime is a random variable［J］.Systems Engineering and Electronics，1996，18（1）：55- 67.（周源泉，翁朝曦，葉喜濤.論加速系數與失效機理不變的條件—（Ⅰ）壽命型隨機變量的情況［J］.系統工程與電子技術，1996，18（1）：55- 67.）

洪東跑（198-3- ），男，高級工程師，博士，主要研究方向為飛行器總體設計、可靠性工程。

E-mail：hloving＠163.com

許 諾（198-6- ），男，工程師，碩士，主要研究方向為飛行器總體設計。

E-mail：xunuo86＠yeah.net

金 晶（198-6- ），女，工程師，碩士，主要研究方向為飛行器總體設計。

E-mail：jinj＠163.com

張海瑞（197-2- ），男，研究員，博士，主要研究方向為飛行器總體設計。

E-mail：zhangcorrs＠sohu.com

LRU spare parts programming for missile based on mission profile

HONG Dong-pao，XU Nuo，JIN Jing，ZHANG Hai-rui
（China Academy of Launch Vehicle Technology，Beijing 100076，China）

Spare parts programming plays an important role in the missile integrated logistic support.To improve the spare sufficiency，the influence of varied environment conditions on missile life is studied.The Poisson process is introduced to describe the maintenance status of the missile line replaceable unit（LRU）in whole life cycle，and a spare parts programming method of missile line replaceable LRU is proposed based on mission profile.The influence of varied mission profiles on LRU reliability is analyzed，and the LRU spare model is established by using the Poisson process.Furthermore，due to the LRU spare parts storage failures and term detecting loss，the spare model is modified.The proposed method is used for the tactical missile LRU spare parts programming.The result shows that the method is able to program the LRU efficiently，satisfy the missile system availability requirement and economize the whole life cycle charge.

missile；environment condition；line replaceable unit（LRU）；spare parts；mission profile

TP 391.9

A

10.3969／j.issn.1001-506X.2015.11.15

1001-506X（2015）11-2520-04

2014- 11- 24；

2015- 04- 25；網絡優先出版日期：2015- 07- 27。

網絡優先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150727.1558.002.html

國家自然科學基金（61104133）資助課題