時敏制導炸彈離散自適應滑模BTT自動駕駛儀設計

李偉明，白宏陽，辛明瑞，申景詩

（1.山東航天電子技術研究所，山東煙臺264003；2.南京理工大學能源與動力工程學院，江蘇南京210094）

時敏制導炸彈離散自適應滑模BTT自動駕駛儀設計

李偉明1，2，白宏陽2，辛明瑞1，申景詩1

（1.山東航天電子技術研究所，山東煙臺264003；2.南京理工大學能源與動力工程學院，江蘇南京210094）

為提高航空時敏制導炸彈控制系統的魯棒性能，增強其大空域作戰能力，將參數估計與離散滑模控制相結合，提出了一種適用于航空時敏制導炸彈傾斜轉彎（bank-to-turn，BTT）自動駕駛儀的離散自適應滑模設計方法。建立了包含參數攝動項的BTT控制仿射模型，針對彈體氣動對稱與交叉耦合等特性，利用反饋線性化方法實現了原系統的解耦控制，并得到了參數化的離散滑模控制律；基于Lyapunov穩定性理論設計了控制器參數的自適應規律，有效克服了各動力學系數偏差引起的不確定擾動。仿真結果表明，所設計的離散自適應滑模BTT控制系統實現了各通道的解耦控制，能有效解決含有較大程度氣動不確定性時炸彈的指令跟蹤控制問題，并且消除了常規滑模控制的抖振現象。

時敏制導炸彈；傾斜轉彎自動駕駛儀；離散趨近律；離散自適應滑模控制

0 引 言

與常規炸彈相比，航空時敏制導炸彈具有射程遠、精度高等優點；同時，為能對時敏目標實施有效打擊，其在彈道末段采用傾斜轉彎（bank-to-turn，BTT）控制模式，同時利用雙向數據鏈路進行“人在回路”的目標識別與制導方式切換，具有較大的靈活性，可滿足未來聯合信息作戰的需求。然而，其控制與制導模式、結構特點給系統帶來較強的通道耦合、傳輸噪聲及氣動參數攝動，故近年來國內外相關學者在解決上述問題中多采用如魯棒［1］、反演［2］、動態逆［3-4］以及滑模控制［56］等非線性控制方法。其中，滑模控制（sliding mode control，SMC）因其克服參數攝動的良好魯棒性能而被廣泛應用于現代制導彈箭的非線性控制系統設計之中［7-10］。

然而，在現代制導彈箭的實際應用過程中，彈上控制單元按給定時鐘節拍進行指令解算，解算方法及采樣頻率對控制效果影響顯著，而基于連續時間系統理論設計的彈載控制器的控制性能將有所限制。因此，為使實際控制性能接近于理論仿真結果，研究制導炸彈BTT自動駕駛儀的離散滑模控制（discrete-time sliding mode control，DSMC）方法具有重要的工程價值。文獻［11］設計了具有模型不確定和時變干擾的線性離散時滯網絡導彈控制系統的離散滑模控制器，有效降低了系統抖振。文獻［12］則著重分析了快速輸出采樣技術對導彈姿態離散變結構控制系統的影響。

由于連續時間系統的SMC理論難以直接應用于實際的離散時間系統設計之中，故本文在BTT控制仿射模型中考慮參數攝動項，利用反饋線性化方法對原系統解耦并推導了離散虛擬控制律，并在文獻［11- 12］控制算法的基礎上，將自適應控制與DSMC進行結合，設計了時敏制導炸彈的離散自適應滑模（discrete-time adaptive sliding mode control，DASMC）BTT自動駕駛儀。仿真結果表明，該設計方法可顯著減小控制抖振，改善閉環系統的動態特性，進而驗證了該自動駕駛儀的穩定性與抑制參數攝動的魯棒性能。

1 BTT控制仿射模型建立

忽略攻角α、側滑角β等二階小量影響，不考慮舵機動力學特性，建立如下包含參數不確定性和外部干擾的BTT控制仿射模型方程：

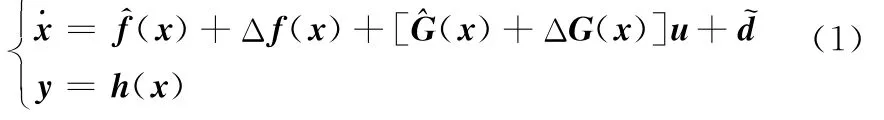
式中，狀態變量x＝［γ，ny，nz，ωx，ωz，ωy］T；控制輸入u＝［δx，δz，δy］T；參考輸出y＝［γr，nyr，nzr］T為外部干擾。估計函數向量及估計增益矩陣^G（x）分別為

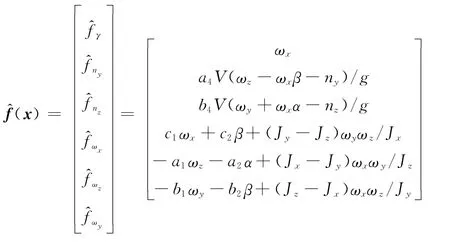
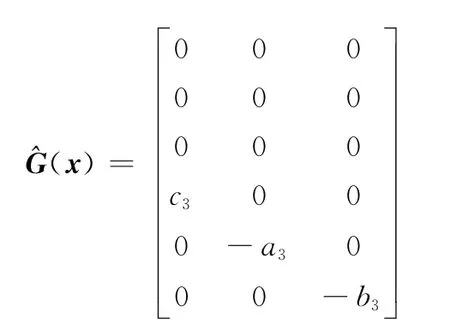
式中，Δai、Δbi及Δcj為各動力學系數的偏差項。

2 制導炸彈離散自適應滑模BTT控制器設計

2.1 精確反饋線性化解耦

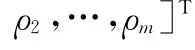
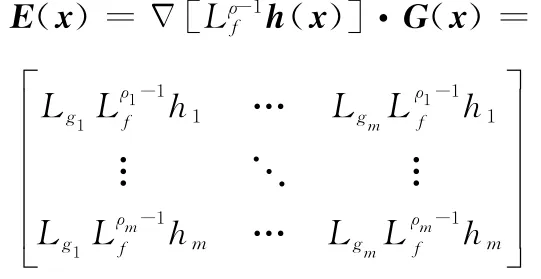
可逆，因此，通過非線性輸入變換可得到系統的解耦控制律為

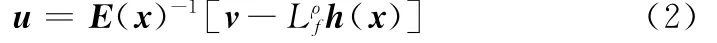
式中，E（x）為解耦矩陣。則式（1）所示的多輸入多輸出非線性系統則轉化為m個獨立的線性動態方程

易知，式（3）中m＝3、ρi＝2，即可解耦為3個獨立的二階子系統進行控制，則系統式（1）的Lyapunov微分系數向量可表示為

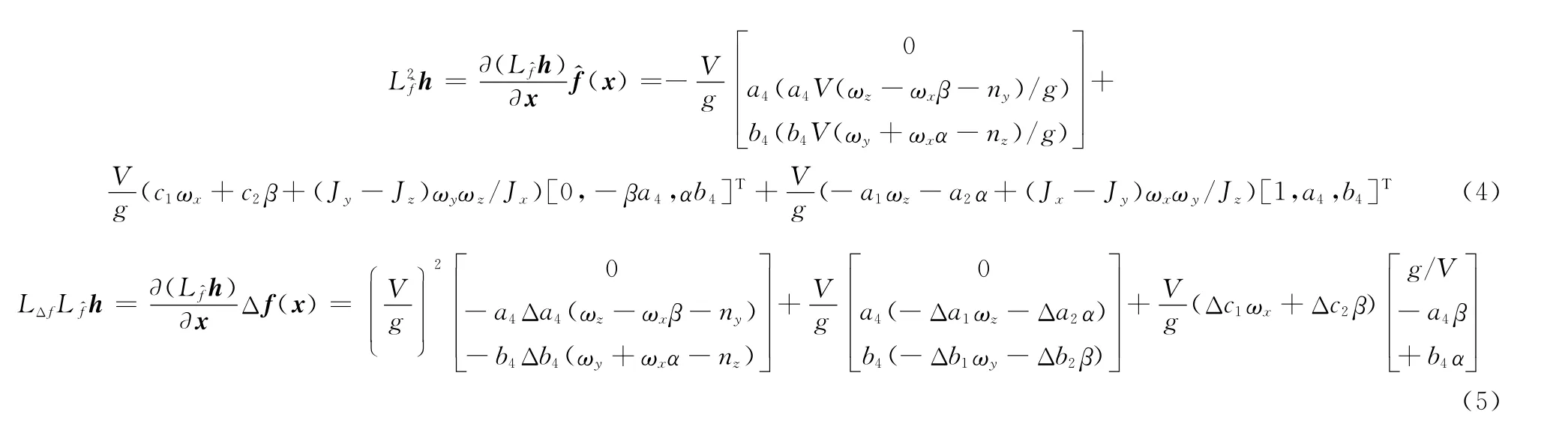
非線性解耦矩陣可表示為

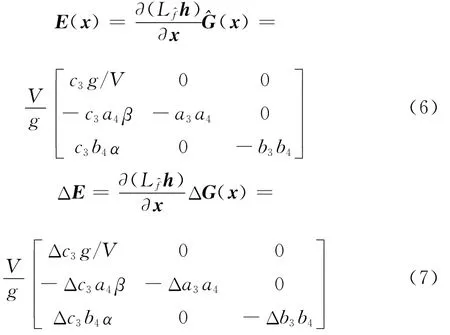
2.2 離散滑模BTT控制器設計

設原連續時間系統的狀態空間矩陣（A，B）完全可控，則系統內任意相鄰采樣周期［k T，（k＋1）T］內的離散化狀態轉移矩陣及增益矩陣可表示為

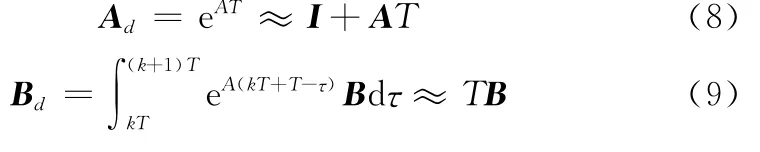
經反饋線性化解耦后，系統的輸出跟蹤指令在新坐標系下可表示為

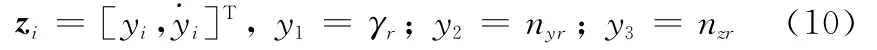
假設系統式（1）中的不確定性擾動項滿足｜d～i｜＜Di（?Di＞0），則式（3）所示線性子系統可離散化表示為

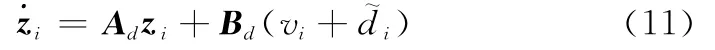
式中，系數矩陣表示為

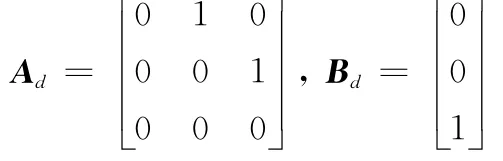
則該制導炸彈BTT控制系統各解耦子系統的離散化狀態方程可描述為

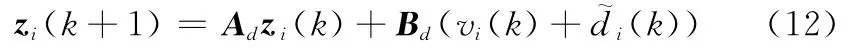
其中，模型不確定擾動項可表示為

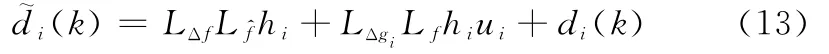
式中，di（k）為非參數外部擾動。

設λ＞0，C＝［λ，1］，結合非線性離散狀態方程式（12），選取如下線性切換函數作為系統式（1）的滑模面S：

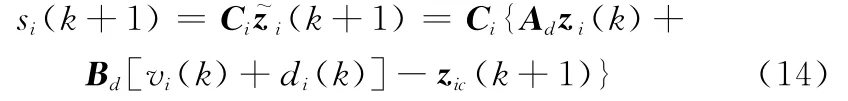
式中，zic（k＋1）為（k＋1）T時刻的輸出指令。

由于受采樣周期T的影響，滑模運動通常在滑模面上反向穿越，為使從任意初始狀態出發的離散時間系統式（12）的運動于有限時間內收斂到準滑動模態，定義一個包圍切換面的切換帶［14］（其帶寬為｜2Δ｜）

為對滑模控制抖振加以抑制，通過邊界層對控制的不連續性進行平滑［15］。同時假設采樣時間較小，則有CiBid≈T，故可選取離散化飽和型指數趨近律

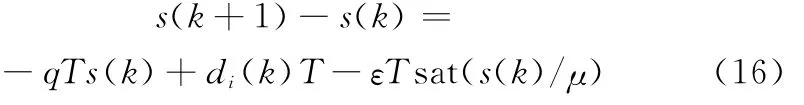
式中，ε＞0為切換增益；q＞0為趨近律系數，且滿足1－qT＞0；μ為邊界層厚度。

綜合式（12）、式（14）及式（16），可得離散滑模虛擬控制律為

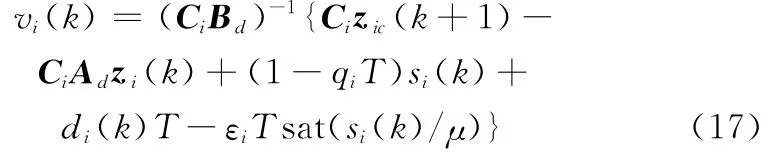
式中，子系統切換增益應設置為εi≥Di＋ηi（ηi＞0）。

由式（15）、式（17）可計算各解耦子系統切換面的切換帶寬

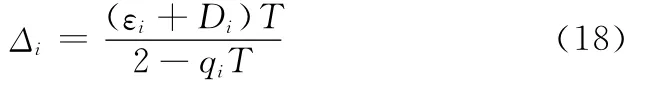
2.3 參數自適應律設計及穩定性分析

為解決在采樣頻率受限情況下較大模型參數攝動帶來的滑動模態不收斂問題，考慮在離散滑模控制中引入自適應控制機制，同時引入零階保持器以確保系統各狀態量在同一采樣周期內維持不變，其離散自適應滑模BTT控制系統結構如圖1所示。

將式（13）改寫為參數誤差向量形式

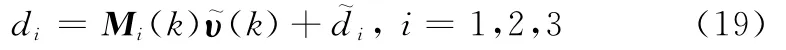
即

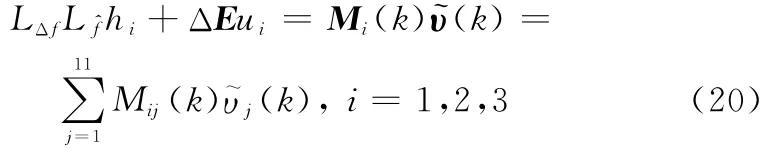
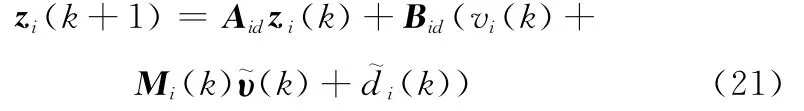
則式（14）可進一步改寫為

采用虛擬控制律式（17），代入式（21）可得

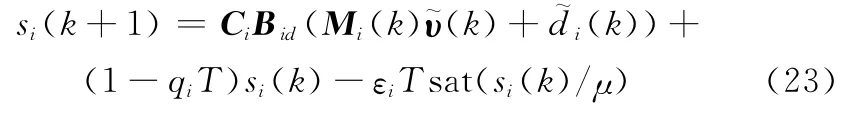
則增量Δsi（k＋1）可表示為

式中

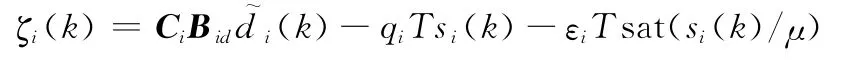
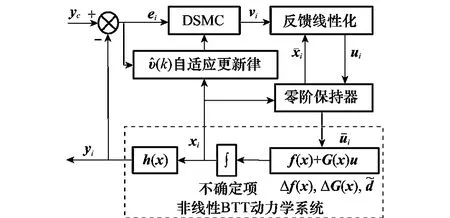
圖1 炸彈離散自適應滑模BTT控制系統結構框圖

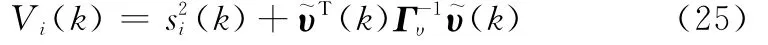
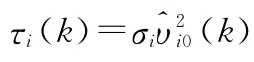
采用式（17）的離散滑模虛擬控制律，并設計參數自適應更新律為

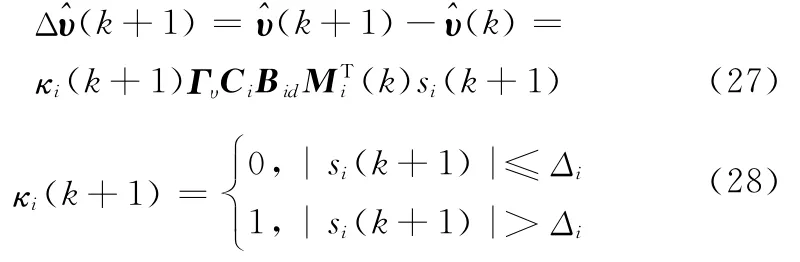
式中，Δi為各解耦子系統切換面的切換帶寬。當si（k）在切換帶以內（k＋1）＝0，參數停止更新，參數誤差項趨于平穩。而在切換帶以外時，激發對象模型參數自適應更新規律。另外，趨近律系數qi、采樣時間T及切換增益εi等均對指令跟蹤精度及系統穩定性有影響，如qi主要影響切換函數的動態過程；T則與模態收斂速度成反比，與穿越理想滑模面的次數成正比，隨著采樣率的下降，系統穩定性也變差；εi則反應了克服系統參數攝動及外部干擾等不確定性的能力，當εi＞，系統狀態滿足｜si（k）｜＞Δi時，采用傳統的純滑模控制將使得

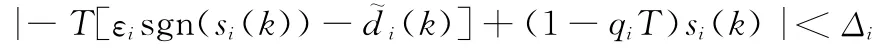
而當｜si（k＋1）｜＞Δi時，則有

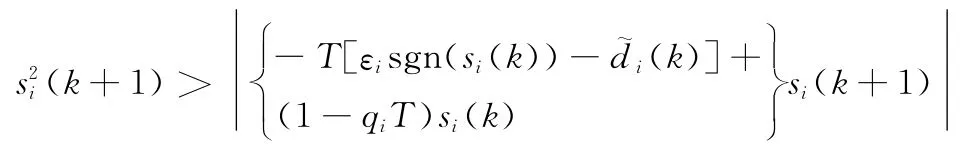
即ΔVi（k＋1）≤0，從而證明控制系統穩定，誤差可有效收斂。

3 離散自適應滑模控制器性能仿真與分析

為驗證離散參數自適應更新律對降低系統控制抖振、抑制系統參數漂移以及對參數攝動的魯棒性能，進行兩組對比仿真：在DSMC方法中設定采樣周期T＝10 ms，滑模面增益λ1＝6.5、λ2＝λ3＝8.0，切換增益ε1＝0.25、ε2＝ε3＝0.5，ηi＝0.1，趨近律系數qi＝5，邊界層厚度μ＝0.05、外界不確定干擾上界D1＝0.05、D2＝D3＝0.075；而在DASMC方法中，控制器參數不變，自適應因子設定為σ1＝0.7、σ2＝σ3＝0.85。

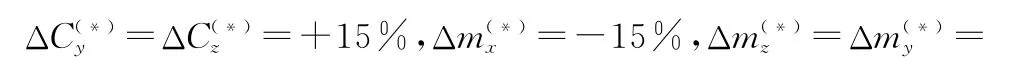
表1 彈體各靜參數標準值

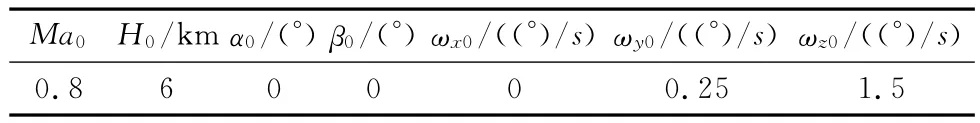
表2 彈道仿真各初始參數

過載指令跟蹤響應對比曲線如圖2所示，其中法向過載nyc為正弦輸入，側向過載nzc則為零輸入。對γc＝60°的滾轉角指令的跟蹤響應曲線如圖3所示。由圖中可看出，當T相同時，DASMC方法對指令跟蹤的快速性更好，跟蹤精度也更高。

對應攻角及側滑角狀態響應曲線如圖4所示，從圖中可以看出，在氣動參數相對于先驗值存在攝動的情況下，DASMC方法可使側滑角保持在±3°以內，滿足BTT控制的性能要求。而DSMC方法由于控制抖振的存在，使得攻角及側滑角狀態量變化趨勢波動較大，特別是側滑角，由于對過載指令nzc跟蹤誤差的積累，使得側滑角的值在跟蹤后期不斷變大，超出BTT控制對于偏航通道的約束要求。

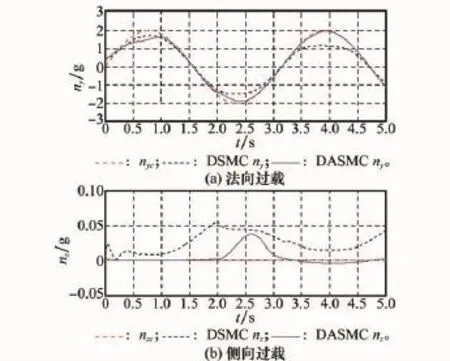
圖2 過載指令跟蹤響應

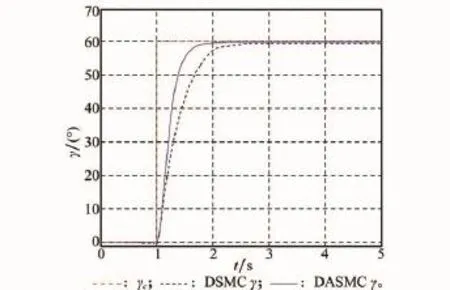
圖3 滾轉角指令跟蹤響應

圖4 攻角與側滑角狀態響應對比曲線

圖5和圖6為三通道角速率狀態響應對比曲線，從圖中可以看出，采用DSMC方法時，由于各通道控制舵偏存在不同程度的控制抖振，因而對應通道的角速率狀態量存在著一定程度的振蕩。而采用DASMC方法時，角速率狀態量變化則較為平緩，振蕩現象得以改善。

圖7和圖8顯示了采用兩種方法時的舵偏量對比曲線，采用DSMC方法時，舵偏量存在明顯的控制抖振，而DASMC方法可對模型參數進行較好的自適應調整，從而有效消除高頻抖振，降低跟蹤誤差。圖9和圖10分別為兩種方法下對應的滑模面切換函數對比規律曲線。圖11～圖13分別為在采樣周期相同時，各通道指令跟蹤的相軌跡對比曲線。從圖中可以看出，采用DASMC方法時，各通道軌跡均能有效地收斂于滑模面附近較小的區域，進而使得切換函數能收斂于較小的切換帶內，從而保證穩態時系統沿準滑模面運動，達到跟蹤控制的目的。在趨近律速率參數qi相同的情況下，兩種方法中系統達到滑模面的速度幾乎相同。而由于采樣周期的影響，采用DSMC方法時，由初始狀態出發的滑模運動在切換面上來回反向穿越，進而對跟蹤精度造成一定的損失。

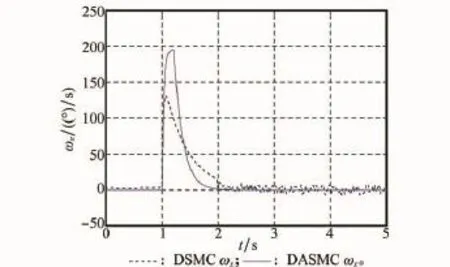
圖5 滾轉角速率狀態響應對比曲線

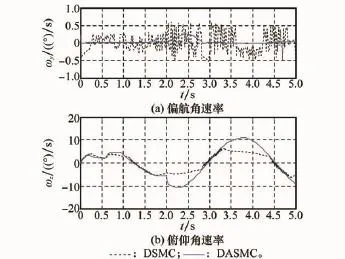
圖6 偏航、俯仰角速率狀態響應對比曲線

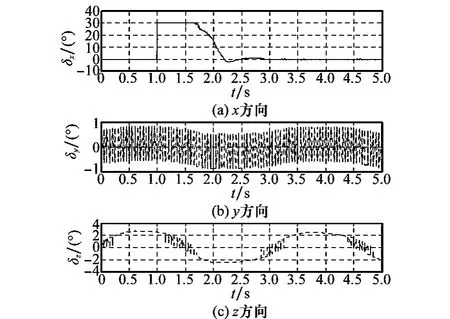
圖7 舵偏曲線（DSMC）

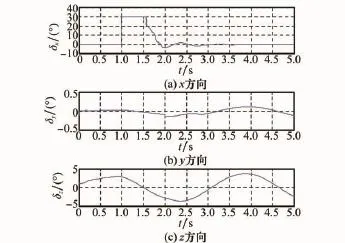
圖8 舵偏曲線（DASMC）

圖9 DSMC切換函數曲線

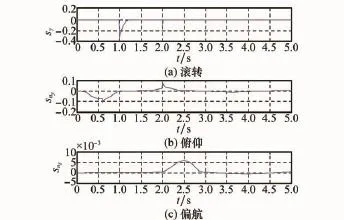
圖10 DASMC切換函數曲線

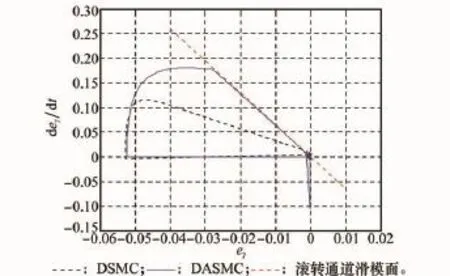
圖11 滾轉通道滑模面相軌跡對比曲線

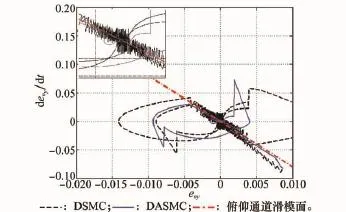
圖12 俯仰通道滑模面相軌跡對比曲線

圖13 偏航通道滑模面相軌跡對比曲線

4 結束語

本文研究了航空時敏制導炸彈BTT自動駕駛儀的離散自適應滑模設計方法，建立了考慮參數攝動項的BTT仿射模型，在利用反饋線性化理論對原非線性耦合之后，通過離散化狀態轉移矩陣及增益矩陣對子系統進行離散化處理。基于離散飽和趨近律推導了虛擬控制律，之后將參數自適應律與離散滑模控制律相結合，設計了該制導炸彈的BTT自動駕駛儀，以消除抖振，同時滿足對參數時變特性的自適應估計性能。對比仿真結果表明，當氣動參數存在較大攝動時，所設計的離散自適應BTT控制系統滿足了對指令跟蹤的魯棒性能。該設計方法可為控制系統的工程化實現提供一定的理論參考。

［1］Lee C H，Chung M J.Gain-scheduled state feedback control design technique for flight vehicles［J］.IEEE Trans.on Aerospace and Electronic Systems，2001，37（4）：173- 182.

［2］Lee T，Kim Y D.Nonlinear adaptive flight control using backstepping and neural networks controller［J］.Journal of Guidance，Control and Dynamics，2001，24（4）：675- 682.

［3］Zheng J H，Luan Z W，Cui P Y，et al.Autopilot design for a bankto-turn missile using the inverse nyquist array method［C］∥Proc.of the AIAA Guidance，Navigation and Control Conference，1993：1642- 1647.

［4］Chris M M，Zhu J J，Zhang T Q.Bank-to-turn roll-yaw-pitch autopilot design using dynamic nonlinear inversion and PD-eigenvalue assignment［C］∥Proc.of the American Control Conference，2000：1359- 1364.

［5］Tong C X，Wang Z J，Zhang T Q.Decoupling system design based on variable structure system for BTT missile［J］.Journal of Astronautics，2006，27（1）：27- 30.（童春霞，王正杰，張天橋.BTT導彈的變結構解耦控制系統設計［J］.宇航學報，2006，27（1）：27- 30.）

［6］Zhang Y X，Dong C Y，Wang Q，et al.Decentralized adaptive sliding mode decoupling control scheme for bank-to-turn missile［J］.Acta Armamentarii，2010，31（7）：906- 910.（張穎昕，董朝陽，王青，等.傾斜轉彎導彈的分散自適應滑模解耦控制方案［J］.兵工學報，2010，31（7）：906- 910.）

［7］Shkolinikov I A，Shtessel Y B.Aircraft non-minimum phase control in dynamic sliding manifolds［J］.Journal of Guidance，Control，and Dynamic，2001，24（3）：566- 567.

［8］Singh S N，Steinberg M L，Page A B.Nonlinear adaptive and sliding mode flight path control of F／A-18 model［J］.IEEE Trans.on Aerospace and Electronic Systems，2003，39（4）：1250- 1261.

［9］Wu P，Yang M.Integrated guidance and control design for missile with terminal impact angle constraint based on sliding mode control［J］.Journal of Systems Engineering and Electronics，2010，16（4）：56- 60.

［10］Shtessel Y B，Shkolnikov I A，Levant A.Guidance and control of missile interceptor using second-order sliding modes［J］.IEEE Trans.on Aerospace and Electronic Systems，2009，45（1）：110- 124.

［11］Yu C L，Xu H L.Discrete-time sliding mode controller for linear time-varying systems with network induced time delay and application to missile attitude control system［J］.Aerospace Control，2008，26（6）：33- 37.（禹春來，許化龍.非匹配不確定網絡離散滑模控制及在導彈姿態控制中的應用［J］.航天控制，2008，26（6）：33- 37.）

［12］Menon P K，Sweriduk G D，Vaddi SS.Nonlinear discrete-time design methods for missile flight control systems［C］∥Proc.of the AIAA Guidance，Navigation，and Control Conference，2004：AIAA 2004- 5326.

［13］Tang Y H.BTT missile robust H∞autopilot design［D］.Xian：Polytechnical University，2004.（湯一華.BTT導彈魯棒H∞自動駕駛儀［D］.西安：西北工業大學，2004.）

［14］Gao W B.Variable structure control theory and design method［M］.Beijing：Science Press，1996.（高為炳.變結構控制理論與設計方法［M］.北京：科學出版社，1996.）

［15］Yang R J，Yang H，Liang X D，et al.Control system design for guidance projectile based on adaptive sliding mode control［J］.Journal of Ballistics，2012，24（3）：75- 79.（楊榮軍，楊樺，梁旭棟，等.基于自適應滑模的制導炮彈控制系統設計［J］.彈道學報，2012，24（3）：75- 79.）

白宏陽（1985- ），通信作者，男，講師，博士，主要研究方向為先進彈箭控制、GPS／INS組合導航、傳遞對準系統設計。

E-mail：hongyang＠njust.edu.cn

辛明瑞（196-1- ），男，研究員，博士，主要研究方向為制導控制系統設計、航天器導航、通信系統設計。

E-mail：pachyrhizuscat＠163.com

BTT autopilot design for time-sensitive guided bombs based on adaptive discrete-time sliding mode control

LI Wei-ming1，2，BAI Hong-yang2，XIN Ming-rui1，SHEN Jing-shi1
（1.Shandong Aerospace Electro-Technology Institute，Yantai 264003，China；2.School of Energy and Power Engineering，Nanjing University of Science and Technology，Nanjing 210094，China）

In order to improve the robustness performance and enhance the large-space combat capability of the airborne time-sensitive guided bombs，a discrete-time adaptive bank-to-turn（BTT）autopilot design method is proposed by combining a parameter estimation scheme with the discrete-time sliding mode control.The BTT control affine system containing parameter perturbation items is modeled.Meanwhile，aiming at the aerodynamic parameter symmetry and cross coupling characteristics，input-output feedback linearization is utilized to decouple the system，and a parametric discrete-time sliding mode control law is obtained.The parametric adaptation law designed based on Lyapunov stability theory can overcome the uncertain disturbances caused by aerodynamic coefficient deviation items effectively.The simulation results indicate that the adaptive discrete-time sliding mode BTT control system proposed is robust to the large-scale aerodynamic parametric uncertainty and has excellent dynamic tracking performance with no control chattering.

time-sensitive guided bombs；bank-to-turn（BTT）autopilot；discrete reaching law；discretetime adaptive sliding mode control

TP 413

A

10.3969／j.issn.1001-506X.2015.11.24

李偉明（1985- ），男，工程師，博士，主要研究方向為飛行力學、先進彈箭制導與控制技術。

E-mail：lee_weiming＠163.com

1001-506X（2015）11-2579-07

2014- 12- 24；

2015- 03- 25；網絡優先出版日期：2015- 05- 13。

網絡優先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150513.1130.006.html

江蘇省自然科學基金（BK20140795）；總裝預研基金（9140A31010114JB25465）；中國航空科學基金（20145159002）；中國航天五院CAST創新基金（CAST2014－27）；中國博士后科學基金（2014 M562568）資助課題