復合高斯雜波中極化MIMO雷達的自適應檢測

趙宜楠，姜智卓，唐晨亮，周志權

（1.哈爾濱工業大學（威海）信息與電氣工程學院，山東威海264209；2.北京遙感設備研究所，北京100854）

復合高斯雜波中極化MIMO雷達的自適應檢測

趙宜楠1，姜智卓1，唐晨亮2，周志權1

（1.哈爾濱工業大學（威海）信息與電氣工程學院，山東威海264209；2.北京遙感設備研究所，北京100854）

基于復合高斯雜波紋理分量服從逆伽馬分布的假設和分布式極化多輸入多輸出（multiple-input multiple-output，MIMO）雷達陣元特點，建立了雷達極化信號模型，提出了一種基于最大后驗概率（maximum a posteriori，MAP）估計和廣義似然比檢驗（generalized likelihood ratio test，GLRT）的MIMO雷達極化檢測器（MAP-GLRT），該檢測器利用了輔助數據估計雜波協方差矩陣以實現自適應性。通過推導檢測器的虛警概率表達式，表明其相對于雜波能量具有恒虛警特性。仿真結果表明，雜波形狀參數和雷達信道數量會對MAP-GLRT檢測器的檢測性能產生影響；相比于其他檢測器，MAP-GLRT檢測器在檢測性能上更有優勢。

多輸入多輸出雷達；自適應檢測；極化；復合高斯；逆伽馬

0 引 言

分布式多輸入多輸出（multiple-input multiple-output，MIMO）雷達也稱為統計MIMO雷達，發射陣元、接收陣元間隔分布且間距較大，可以利用空間分集，即目標散射截面積（raclar cross section，RCS）的空間特性來提高目標的檢測性能［13］。復雜雷達目標的RCS是角度的快變函數，目標閃爍會導致信號衰減，使雷達性能惡化，而當多個發射陣元和接收陣元充分分離時，由于目標散射的不相關性，每個通道的信號攜帶相互獨立的信息，所有信號均衰減的概率較低，減小了目標閃爍的影響，進而提高了雷達性能。極化分集技術是基于水平和垂直極化分量不相關提出的，是現代雷達研究的一個重要方向，將極化分集應用到空間分集的分布式MIMO雷達系統中，必定可以進一步提高雷達系統的檢測性能［3］。

文獻［4］首先推導了檢測概率及克拉美羅界的等價表達式，而后聯合最大化主旁瓣差約束，并對檢測概率、參數估計方差及旁瓣3個約束條件加權，提出一種提高MIMO雷達檢測和參數估計性能的波形優化方法；文獻［5- 8］在高斯雜波背景下，研究了分布式MIMO雷達利用空間分集增益克服目標閃爍的問題，與相控陣雷達、多輸入單輸出雷達等多種雷達系統進行了比較，證明了分布式MIMO雷達檢測性能的優越性；文獻［9］基于廣義似然比檢驗，提出了一種復合高斯雜波中距離分布目標的極化自適應檢測器，推導了檢測器的虛警概率表達式，說明了其相對于復高斯雜波的協方差矩陣和紋理分量具有恒虛警特性；文獻［10］首先分析了對角加載自適應匹配濾波器和對角加載自適應相干估計器的檢測性能，然后推導了虛警概率和檢測概率的表達式，仿真驗證了在訓練樣本不足的情況下，二者檢測性能大為提高；文獻［11］將極化引入分布式MIMO雷達，推導了高斯雜波背景下的極化NP檢測器，仿真驗證了相比于傳統分布式MIMO雷達，極化雷達系統在檢測性能上的優勢；文獻［12］主要研究了協方差矩陣未知的復合高斯雜波下分散目標的極化MIMO雷達檢測問題，文章基于廣義似然比檢驗，通過引出3種估計雜波協方差矩陣的方法來設計自適應檢測器，仿真驗證了空間分集和極化分集可以大大提升雷達的檢測概率；文獻［13］研究了復合高斯雜波下分散目標的極化MIMO雷達檢測問題，利用Rao檢驗和Wald檢驗準則來設計自適應檢測器，通過與廣義似然比檢驗對比論證了Wald檢測器在處理尖峰雜波背景下的目標時具有極好的性能，然而，在低掠角或高分辨力雷達背景下，復合高斯模型更加符合真實雜波信號的分布［14-15］；文獻［16- 17］研究了K分布雜波背景下MIMO雷達的信號檢測算法，提出了單元平均恒虛警（cell avarage-constant false alarm rate，CA-CFAR）檢測器，分析了檢測器的檢測性能。但是實測數據表明，對于嚴重拖尾的雜波，將復合高斯分布的紋理分量建模為逆伽馬分布更加恰當［15］。

本文在紋理分量服從逆伽馬分布的復合高斯（inverse Γ-compound Gaussian，iΓ-CG）雜波背景下，研究了分布式MIMO雷達的自適應極化檢測算法，提出了基于最大后驗概率（maximum a posteriori，MAP）估計和廣義似然比檢驗（generalized likelihood ratio test，GLRT）的自適應極化檢測器（MAP-GLRT），并在此基礎上推導了該檢測器的虛警概率表達式，理論驗證了其恒虛警特性；通過蒙特卡羅仿真，比較了不同形狀參數和信道數量下，該檢測器和協方差矩陣先驗已知（knowledge-aided generalized likelihood ratio test，KL-GLRT）檢測器、非極化自適應檢測器（Neyman Pearson-generatized likelihood ratio test，NP-GLRT）的檢測性能。

1 信號模型

假設目標為靜止點目標，且其散射矩陣依賴于觀測角度；雷達系統由M個發射陣元和N個接收陣元組成，收發陣元均間隔較遠，如圖1所示。

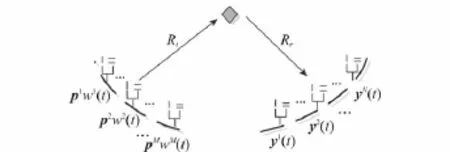
圖1 分布式MIMO雷達系統模型

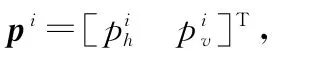
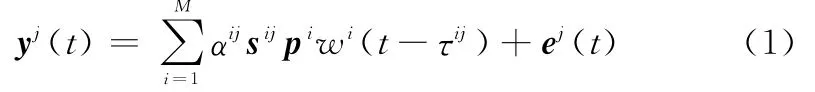
每個接收陣元利用M個匹配濾波器可以將來自不同發射陣元的發射信號分開，得到MN個信道對應的MN個接收信號，表示為

將所有接收信號表示為2MN維列向量，可得

式中

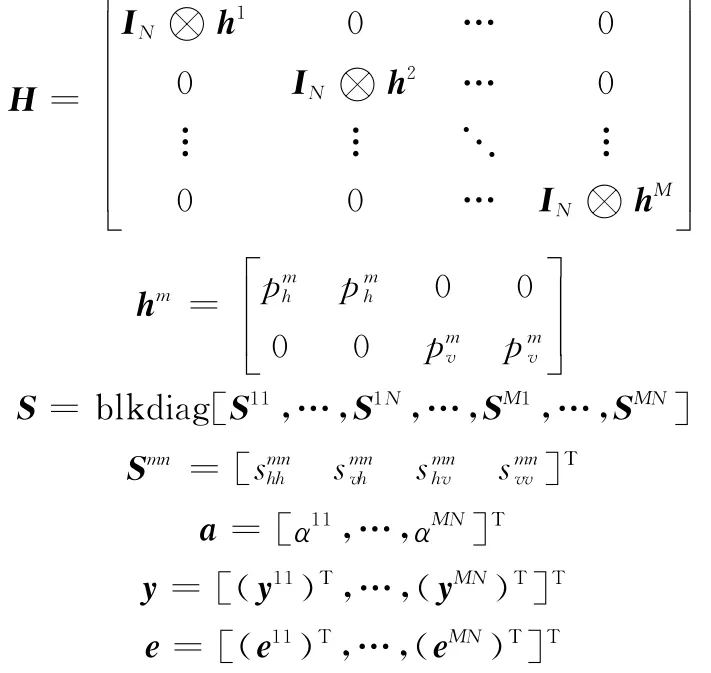
式中，IN表示N維單位矩陣；?表示Kronecker積；blkdiag［·］表示塊對角矩陣。

假設雷達系統發射K個脈沖，在觀測時間內目標靜止，則

式中

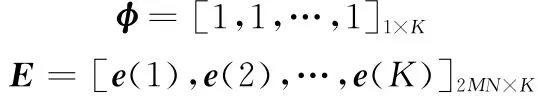
利用iΓ-CG模型建模雜波，即

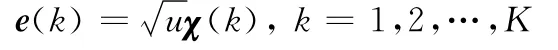
式中，u，χ（k）相互獨立，χ（k）為快變散斑分量，服從均值為0、協方差矩陣為Σ的高斯分布；u為慢變紋理分量，是非負隨機過程，并且1／u服從均值為1，形狀參數為v的伽馬分布，則紋理分量u的概率密度函數［1819］為

式中，Γ（·）表示伽馬函數。

2 檢測器設計

2.1 檢測問題描述

iΓ-CG雜波背景下點目標的檢測問題可以表述為以下二元假設檢驗問題：

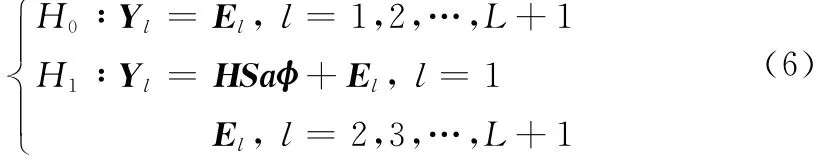
式中，Y1稱為主數據，為可能存在目標的檢測單元數據，選擇主數據相鄰的距離單元Y2，…，YL＋1作為輔助數據，其不存在目標，但與主數據具有相同雜波散斑分量協方差矩陣。H0，H1假設下y（k）的條件分布分別表示為

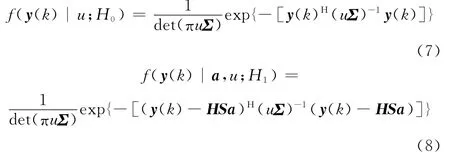
式中，（·）H表示共軛轉置運算；（·）－1表示矩陣求逆運算；det（·）表示矩陣的行列式。

H1假設下y（k）的概率密度函數可以表示為

2.2 MAP-GLRT極化自適應檢測器

在缺少信號傳播衰減和雜波分布完整知識的情況下，采用兩步法廣義似然比檢驗（generalized likelihood ratio test，GLRT），即在似然比檢驗（liklihood ratio test，LRT）中使用未知參數的估計值代替未知參數來解決問題，具體推導過程如下所示。

步驟1將MAP-GLRT檢測器的檢驗統計量表示為

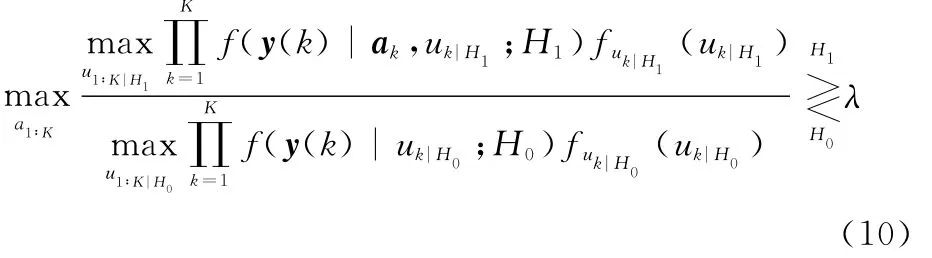
步驟2根據式（10），分別計算H0，H1假設下雜波紋理分量的最大后驗概率（maximum a posteriori，MAP）估計值

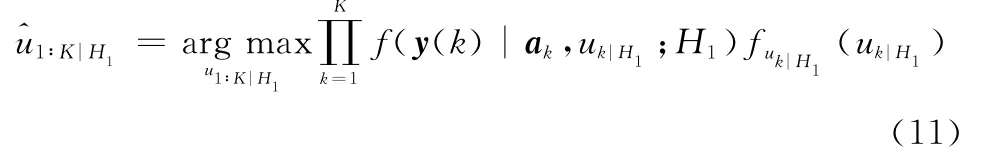
經過求導和化簡式（11），可得

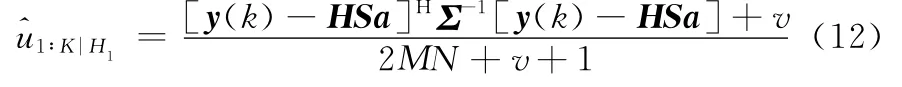
同理可得

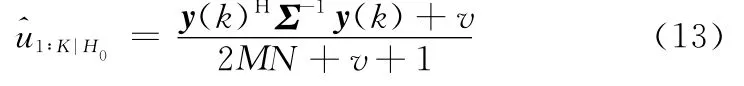
步驟3將式（12）、式（13）代入到式（10）中，得到

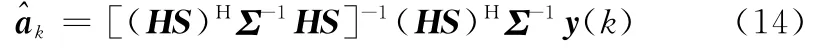
將雜波參數和信號衰減向量的估計值代入到檢驗統計量表達式中，經過化簡可以得到

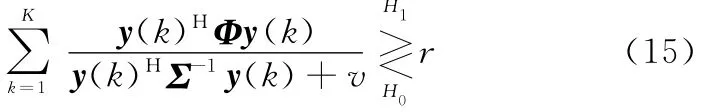
式中

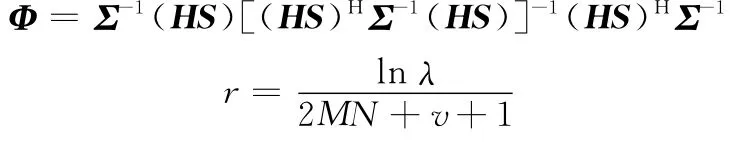
為新門限值。

步驟4為實現檢測器的自適應，需要利用觀測得到的輔助數據對iΓ CG雜波散斑分量的協方差矩陣進行估計。為消除雜波局部能量的影響，上式中的協方差矩陣Σ全部使用歸一化樣本協方差［20］矩陣估計值代替

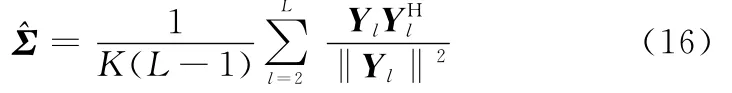
進而，檢驗統計量的最終表達形式為

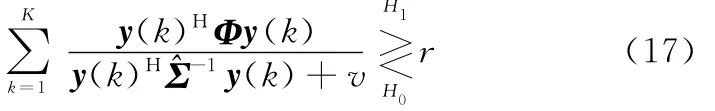
2.3 恒虛警概率分析

首先研究檢驗統計量求和項中的任意一項，用Δ（y（k））表示，將y（k）替換為Σ1／2y′（k），經過化簡可得

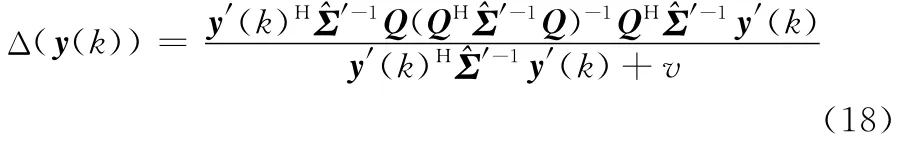
式中

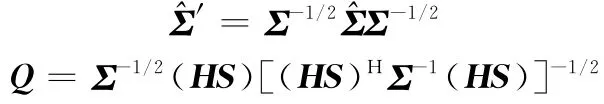
式（18）可以表示［21］為

式中，2η（y（k））和2ξ（y（k））分別服從自由度為2（L－2MN＋1）和4MN的中心χ2分布。則ζ（y（k））服從F分布，即ζ（y（k））～F［2（L－2MN＋1），4MN］，ζ（y（k））和Δ（y（k））的概率密度函數分別為

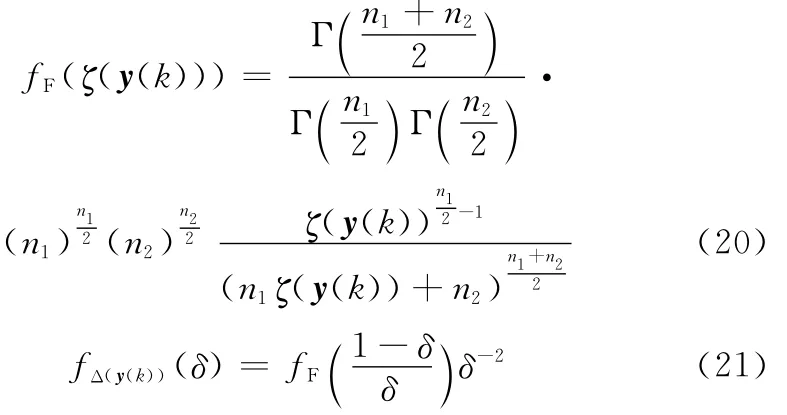
式中，n1＝2（L－2MN＋1）；n2＝4MN。

根據以上推導，檢驗統計量可以表示為

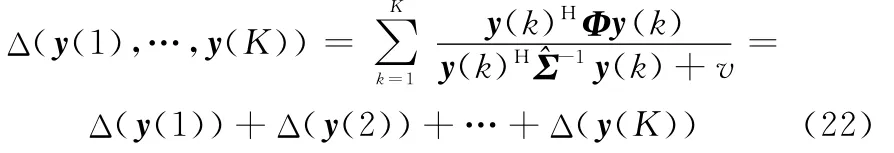
當i≠j，i，j∈｛1，2，…，K｝時，Δ（y（i））與Δ（y（j））相互獨立，因此在H0假設下可得

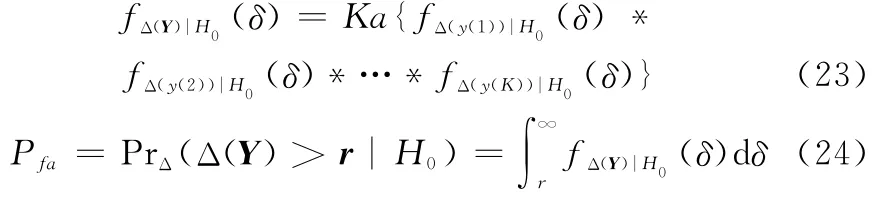
式中，Ka為PDF的歸一化常數；*為卷積運算。由式（20）、式（21）和式（23）均不包含雜波分布相關參數可知，式（24）與雜波分布無關，理論驗證了MAP-GLRT檢測器相對于雜波能量具有CFAR特性。

3 仿真分析

3.1 仿真參數設置

在以下數值實例中，假設分布式MIMO雷達系統由M個發射陣元和N個接收陣元組成，收發天線相隔較遠；目標為靜止的遠場點目標；對于每個發射信號，始終選擇發射陣元數量M＝2，發射脈沖串數K＝40；定義虛警概率Pfa＝10－3，則蒙特卡羅仿真次數由100／Pfa決定。由于水平和垂直極化通道不相關，且雷達系統收發陣元間距較遠，不同收發陣元間的雜波具有低相關性，則散斑分量的空間協方差矩陣為塊對角形式［17］，即Σ＝blkdiag［I2?Σ1，…，I2?ΣM］，Σm（m＝1，2，…，M）為N×N維正定矩陣，其元素為Σm［i，j］＝0.01｜i－j｜（i，j＝1，2，…，N）；目標極化散射矩陣元素符合零均值高斯分布，不同信號傳播通道極化散射矩陣元素對應的高斯分布協方差矩陣為

式中，ε＝1＋j，j表示虛數單位；（·）*表示共軛運算。假設兩個發射機的發射信號為

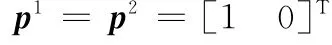
即

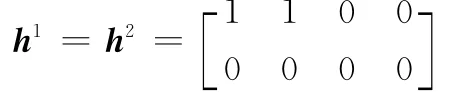
仿真時a的大小由信雜比（signal-to-clutter ratio，SCR）所確定，SCR定義如下：

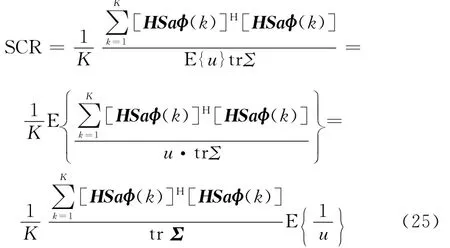
3.2 檢測性能分析

圖2比較了MAP-GLRT自適應極化檢測器和KLGLRT極化檢測器的檢測性能，形狀參數分別取v＝1，2，3，接收陣元數目取N＝2，輔助數據距離單元數L＝20。由圖可以得到以下結論：即使iΓ-CG雜波很強，即SCR很低時（SCR＝－1 dB），MAP-GLRT自適應極化檢測器也能得到較高的檢測性能；形狀參數越大，雜波分布越接近于高斯分布，兩種檢測器的檢測性能越好；MAP-GLRT檢測器相比于KL-GLRT檢測器，檢測性能變差，這是由雜波協方差矩陣先驗知識的缺失導致的。

圖3比較了MAP-GLRT自適應極化檢測器和NP-GLRT檢測器的檢測性能，接收陣元數目分別取N＝2，3，4，形狀參數取v＝1，其他仿真參數設置同上。由圖可以看出，信道數量越大，兩種檢測器的檢測性能越好；由于NP-GLRT檢測器損失了正交極化通道中的能量，MAP-GLRT檢測器的檢測性能相比于NP-GLRT檢測器有大約3 dB的SCR改善。

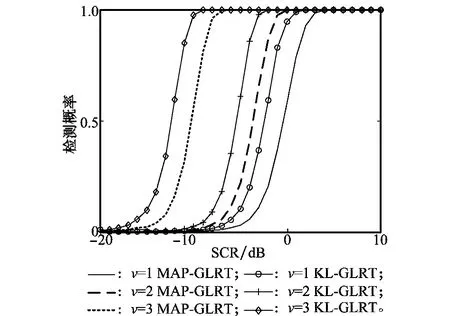
圖2 不同形狀參數下MAP-GLRT和KL-GLRT的檢測性能曲線

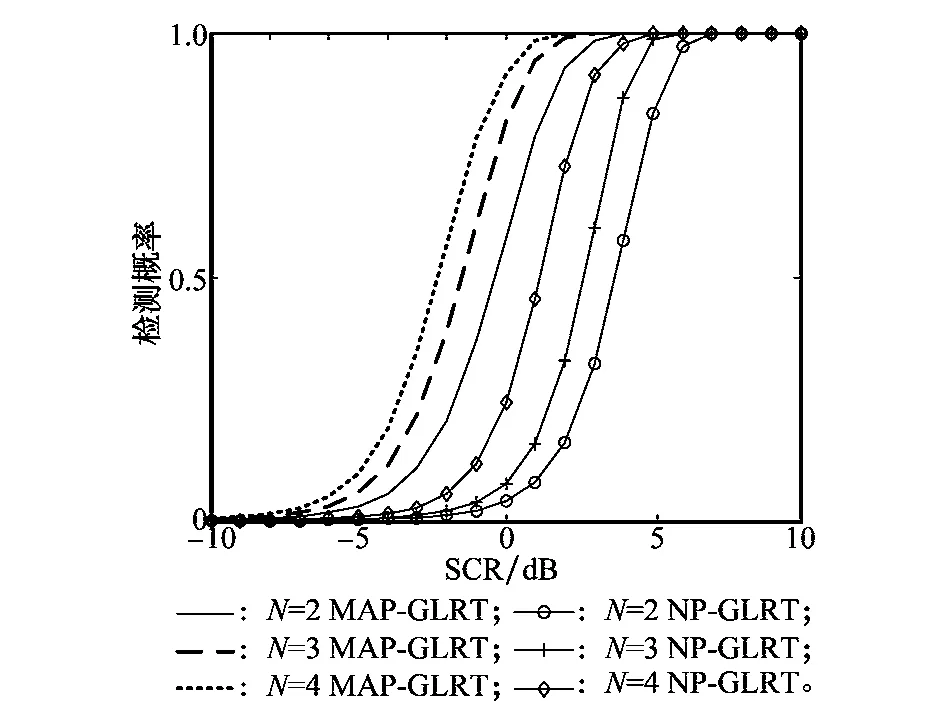
圖3 不同接收陣元數量下MAP-GLRT和NP-GLRT的檢測性能曲線

圖4分析了不同輔助數據距離單元數下MAP-GLRT自適應極化檢測器的檢測性能曲線，輔助數據距離單元數分別取L＝10，20，30，其他仿真參數設置同上，由圖可以看出，輔助數據距離單元數越多，對雜波的協方差矩陣估計的越精確，檢測器的檢測性能就越好。

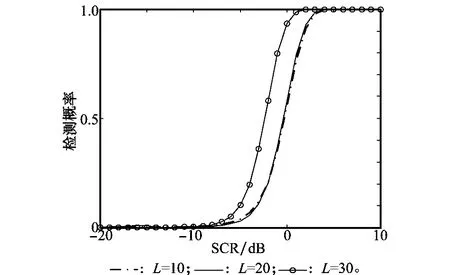
圖4 不同輔助數據距離單元數下MAP-GLRT自適應極化檢測器的檢測性能曲線

圖5分析了不同形狀參數對應的MAP-GLRT檢測器虛警概率特性，假設取值不同的紋理分量均值E［u］代表雜波能量的起伏，形狀參數v分別取1、2、3，接收陣元數目取N＝2，其他仿真參數設置同上。由圖可知，不同形狀參數下MAP-GLRT檢測器相對于雜波能量都具有CFAR特性，與第3.3節的理論推導一致。

圖5 不同形狀參數下CFAR與紋理分量均值的關系

4 結 論

本文提出了一種iΓ-CG雜波背景下的極化MIMO雷達的自適應檢測器（MAP-GLRT），該檢測器將極化分集與空間分集相結合進一步提高了分布式MIMO雷達的檢測性能，理論分析驗證了其相對于雜波能量具有CFAR特性。利用蒙特卡羅仿真，分析了形狀參數和信道數量對MAP-GLRT檢測器檢測性能產生的影響。通過比較MAP-GLRT檢測器與KL-GLRT檢測器的檢測性能，驗證了雜波協方差矩陣先驗知識的缺失使MAP-GLRT檢測器的檢測性能略有下降；又分析了不同輔助數據距離單元數下檢測性能的不同，指出輔助數據越多，對于雜波協方差矩陣的估計越精確，檢測性能就會越好；通過比較MAP-GLRT檢測器和NP-GLRT自適應檢測器的檢測性能，證明了MAP-GLRT檢測器檢測性能的優越性；通過分析不同形狀參數下雜波能量與虛警概率的關系，進一步驗證了MAP-GLRT檢測器的CFAR特性。

［1］Zhou S H，Liu H W.Scattering properties of spatial and frequency diversity of MIMO radar targets［J］.Journal of Electronics&Information Technology，2010，32（1）：39- 42.（周生華，劉宏偉.MIMO雷達目標空間和頻率散射多樣性研究［J］.電子與信息學報，2010，32（1）：39- 42.）

［2］Haimovich A M，Blum R S，Cimini L J.MIMO radar with widely separated antennas［J］.IEEE Signal Processing Magazine，2008，25（1）：116- 129.

［3］Liao Y Y，He Z S.Study on stealth target detection performance of polarimetric MIMO radar［J］.Journal of Application Research of Computers，2012，29（2）：246- 249.（廖羽宇，何子述.極化MIMO雷達隱身目標檢測性能研究［J］.計算機應用研究，2012，29（2）：246- 249.）

［4］Zhang X Y，Liao G S，Xu J W，et al.Waveform design for MIMO radar to improve target detection and parameter estimation［J］.Systems Engineering and Electronics，2014，36（8）：1494- 1499.（張向陽，廖桂生，許京偉，等.提高MIMO雷達檢測和參數估計性能的波形設計［J］.系統工程與電子技術，2014，36（8）：1494- 1499.）

［5］Wang F，Cao N，Liu W.Detection performance of MIMO radar with un-known parameters［C］∥Proc.of the 8th International Conference on Wireless Communications，Networking and Mobile Computing，2012：1- 4.

［6］Zhang T，Cui G，Kong L J，et al.Adaptive Bayesian detection using MIMO radar in spatially heterogeneous clutter［J］.IEEE Signal Processing Letters，2013，20（6）：547- 550.

［7］Ghobadzadeh A，Taban M R，Tadaion A A，et al.Invariant target detection of MIMO radar with unknown parameters［C］∥Proc.of the IEEE 5th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing，2013：408- 411.

［8］Sui K K，Li H，Li X X.MIMO radar detection performance analysis in clutter and noisy environments［J］.Journal of Computer Systems&Applications，2013，22（9）：230- 234.（隋凱凱，李宏，李欣欣.雜波加噪聲環境下MIMO雷達檢測性能分析［J］.計算機系統應用，2013，22（9）：230- 234.）

［9］Wang W G，Zhao Y N，Qiao X L.Polarimetric adaptive detection for range-distributed targets in compound-Gaussian clutter［J］.Journal of Astronautics，2012，31（6）：1138- 1143.（王偉國，趙宜楠，喬曉林.復合高斯雜波中距離分布目標的極化自適應檢測［J］.宇航學報，2012，31（6）：1138- 1143.）

［10］Liu W J，Xie W C，Wang Y L.AMF and ACE detectors based on diagonal loading［J］.Systems Engineering and Electronics，2013，35（3）：463- 468.（劉維建，謝文沖，王永良.基于對角加載的自適應匹配濾波器和自適應相干估計器［J］.系統工程與電子技術，2013，35（3）：463- 468.）

［11］Gogineni S，Nehorai A.Polarimetric MIMO radar with distributed antennas for target detection［J］.IEEE Trans.on Signal Processing，2010，58（3）：1689- 1697.

［12］Cui G L，Kong L J，Yang X B，et al.Distributed target detection with polarimetric MIMO radar in compound-Gaussian clutter［J］.Digital Signal Processing，2012，22（3）：430- 438.

［13］Kong L J，Cui G L，Yang X B，et al.Rao and Wald tests design of polarimetric multiple-input multiple-output radar in compound-Gaussian clutter［J］.IET Signal Processing，2011，5（1）：85- 96.

［14］Mandal S K，Bhattacharya C.Validation of stochastic properties of high resolution clutter data from IPIX radar data［C］∥Proc.of the IEEE International Conference on Intelligent Systems and Signal Processing，2013：251- 255.

［15］Farina A，Gini F，Greco M V，et al.High resolution sea clutter data：statistical analysis of recorded live data［J］.IEE Radar，Sonar and Navigation，1997，144（3）：121- 130.

［16］Sammartino P F，Baker C J，Griffiths H D.MIMO radar performance in clutter environment［C］∥Proc.of the IEEE CIE International Conference on Radar，2006：1- 4.

［17］Sammartino P F，Baker C J，Griffiths H D.Adaptive MIMO radar system in clutter［C］∥Proc.of the IEEE Conference on Radar，2007：276- 281.

［18］Stinco P，Greco M，Gini F.Adaptive detection in compound-Gaussian clutter with inverse-Gamma texture［C］∥Proc.of the IEEE CIE International Conference on Radar，2011：434- 437.

［19］Wang J，Nehorai A.Adaptive polarimetry design for a target in compound-Gaussian clutter［J］.Signal Processing，2009，89（6）：1061- 1069.

［20］Gini F.Performance analysis of two structured covariance matrix estimator in compound-Gaussian clutter［J］.Signal Processing，2000，80（2）：365- 371.

［21］Park H R，Li J，Wang H.Polarization-space-time domain generalized likelihood ratio detection of radar targets［J］.Signal Processing，1995，41（2）：153- 164.

姜智卓（199-4- ），男，碩士研究生，主要研究方向為雷達信號處理、波形設計。

E-mail：hrb_jzz＠163.com

唐晨亮（197-6- ），男，高級工程師，碩士，主要研究方向為彈載星載制導探測技術。

E-mail：tcl_duck7727＠sina.com

周志權（197-3- ），男，教授，博士，主要研究方向為信號與信息處理。

E-mail：zzq＠hitwh.edu.cn

Adaptive detection of polarimetric MIMO radar in compound-Gaussian clutter

ZHAO Yi-nan1，JIANG Zhi-zhuo1，TANG Chen-liang2，ZHOU Zhi-quan1
（1.School of Information and Electrical Engineering，Harbin Institute of Technology（Weihai），Weihai 264209，China；2.Beijing Institute of Remote Sensing Equipment，Beijing 100854，China）

The polarimetric signal model of multiple-input multiple-output（MIMO）radar is formulated，based on the assumption of inverse-Gamma distribution for the texture component of compound-Gaussian clutter.An adaptive polarimetric detector of MIMO radar based on maximum a posteriori estimation and the generalized likelihood ratio test（MAP-GLRT）is proposed.Firstly，the training data are exploited to estimate the covariance matrix of the clutter in the detector to realise the adaptability.Furthermore，the analytic expression of the false alarm probability is derived to prove constant with respect to the clutter energy.Simulation results show that the shape parameter of the clutter and the number of radar channels have an impact on the MAP-GLRT，and the performance of MAP-GLRT is better than its counterparts.

multiple-input multiple-output（MIMO）radar；adaptive detection；polarization；compound-Gaussian；inverse-Gamma

TN 957.51

A

10.3969／j.issn.1001-506X.2015.11.08

1001-506X（2015）11-2474-06

趙宜楠（1977- ），男，教授，博士，主要研究方向為雷達信號處理、自適應波束形成。

E-mail：hrbzyn＠163.com

2014- 09- 23；

2015- 04- 23；網絡優先出版日期：2015- 07- 07。

網絡優先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150707.1404.006.html

國家自然科學基金（61371181）；山東省自然科學基金（ZR2012FQ007）資助課題