旋轉長基線干涉儀的系統偏差聯合估計方法

吳癸周，張 敏，郭福成

（國防科技大學電子科學與工程學院，湖南長沙410073）

旋轉長基線干涉儀的系統偏差聯合估計方法

吳癸周，張 敏，郭福成

（國防科技大學電子科學與工程學院，湖南長沙410073）

針對旋轉長基線干涉儀（rotating long baseline interferometer，RLBI）定位系統中接收通道幅／相不一致性、機械加工誤差、基線的安裝偏差等因素對定位的影響，建立了RLBI系統偏差的模型，證明了基線轉角偏差和轉軸偏角兩種系統偏差的等效性，給出了理論定位偏差的計算方法，指出了引起顯著定位偏差的系統偏差，對此提出了一種基于已知位置標校站的系統偏差聯合估計的高斯牛頓迭代方法。仿真分析表明，該方法的估計性能可達到克拉美-羅下限（Cramer-Rao lower bound，CRLB），基于單標校站估計和標校系統偏差即可顯著提高系統的定位性能。

干涉儀；偏差；估計；旋轉

0 引 言

旋轉長基線干涉儀（rotating long baseline interferometer，RLBI）通過觀測多個不同時刻的模糊相位差可直接實現測向［1- 2］和高精度定位［3- 6］。相對于傳統的多通道干涉儀［7- 9］通過增加器件數量［10- 11］、采用復雜的處理算法［12- 14］解相位差模糊再定位，該技術最少僅需要兩個天線和接收通道，可以有效解決系統復雜度與定位精度之間的矛盾［15- 16］，近年在電子偵察等領域受到廣泛關注。在實際的RLBI系統中，除了受到各類參數測量隨機誤差的影響外，還受各通道幅／相不一致性的影響，會導致相位差測量存在固定的偏差；基線機械加工水平的限制，可能導致實際的基線長度與標稱的基線長度也存在一個偏差；另外，受限于干涉儀的安裝精度，還會出現基線轉角偏差、基線傾角等系統偏差，這些系統偏差在短時間內是固定不變的，可能會造成顯著的定位偏差，因此需對其采用一定手段和方法進行估計，以消除此類誤差。

文獻［17］通過處理干涉儀測量得到的特定數據，可以給出準確的相位誤差概率密度函數以及方差，據此可以從理論上提高干涉儀測量精度，但是并沒有具體分析影響干涉儀測量精度的誤差及其估計或校正方法；文獻［18］提出了一種干涉儀相位一致性校正的方法，該方法主要通過添加一種改進的自檢源，自檢時按照固定步進生成一個動態的校正表，可以滿足不同頻點的通道相位一致性校正，但是在同時存在多種系統偏差的情況下會非常復雜；文獻［19］提出了一種可以大幅減少干涉儀幅相不一致性誤差的校正方法，可以大幅減少相位誤差到2°，但是該方法主要針對多模干涉型耦合器；文獻［20］給出了一種圓陣干涉儀測向的方法，并采用標校源對其相位不一致性進行估計和校正，文獻［21］利用干涉儀結構特點可以估計其幅／相的誤差，但是以上兩篇文獻針對的主要是圓陣排列的干涉儀；文獻［22］基于多個已知位置的標校站，可以同時估計基線轉角偏差和基線長度偏差，但只是針對固定基線干涉儀進行研究，并不能解決RLBI系統偏差的估計問題。文獻［23］對旋轉基線干涉儀在各項誤差條件下的定位精度進行了詳細分析，但是并沒有針對其中的系統偏差提出相應的估計或校正方法；文獻［24］針對時變基線干涉儀系統，提出了一種參數化聯合估計目標位置以及相位差偏差的方法，可以同時估計目標位置以及相位差系統偏差，但并沒有考慮對基線轉角偏差等系統偏差的估計。

本文首先建立了RLBI系統偏差模型，在典型場景下對比分析了各類系統偏差引起的定位偏差，并分析了相位差獨立噪聲條件下各類系統偏差估計理論的克拉美-羅下限（Cramer-Rao lower bound，CRLB），為消除影響較大的系統偏差，提出了一種基于已知位置標校站的系統偏差聯合估計的高斯牛頓（Gauss-Newton，GN）方法，最后通過仿真并與CRLB相對比，驗證了該方法的有效性。

1 RLBI系統偏差模型

在實際的RLBI系統中，根據信號的測量和旋轉面、旋轉軸、參考坐標系之間的關系，RLBI系統偏差可以分為3類：第1類為信號測量系統偏差，主要包括由于干涉儀幅／相不一致性造成的相位差測量系統偏差bφ，該偏差使得測量的相位差存在一個固定偏差；測頻技術受限造成的測頻偏差bf。第2類為基線系統偏差，主要包括因基線機械加工偏差造成的基線長度偏差bd，它會造成基線掃過的圓周半徑增大或減少；因安裝偏差造成的基線轉角偏差bθ，該偏差使得基線的零角度指向與參考坐標軸（如X軸）指向不重合，這將導致基線方位角存在一個固定的偏差，使得基線指向矢量產生時變的偏差；因安裝偏差造成的基線與旋轉軸不正交，這會產生基線垂直傾角ε，該偏差使得旋轉基線掃過的區域形成兩個頂點對接的圓錐，而不是一個圓，該偏差同樣造成基線指向矢量存在時變的偏差。第3類主要由基線的旋轉軸與參考坐標軸（如Z軸）不重合造成的，為描述這一偏差需要兩個偏角，以參考坐標軸Z軸為例，這兩個偏角分別為旋轉軸偏離Y軸的角度ζ，旋轉軸偏離Z軸的角度γ，分別稱之為轉軸偏角和轉軸傾角，定位坐標系先繞Z軸旋轉ζ，然后繞Y軸旋轉γ即可得到定位坐標系。第2類和第3類各項系統偏差如圖1所示，O′為基線中點在XOY平面的投影，OS為轉軸；A1、A2分別為基線兩端的天線，虛點線表示偏大的基線。

實際的RLBI系統，可能3類系統偏差同時存在。

假設觀測的輻射源載頻為fm，相位差為φm，觀測的基線長度為dm，觀測的基線轉角為θm，則有

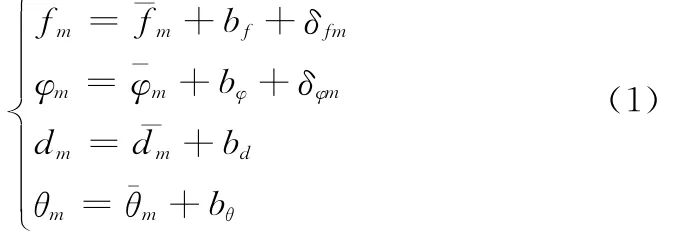
式中，m＝1，2，…，M，M為觀測到的信號次數；δ代表各項隨機誤差，假設所有隨機誤差均滿足零均值高斯分布；b代表各項系統偏差；上劃線代表各項真實值。對應的基線指向矢量為

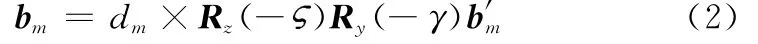
式中

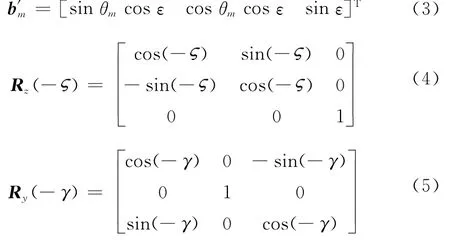
Rz（－ ）和Ry（－γ）分別表示矢量繞Z軸和Y軸旋轉－ 角度（逆時針為正）和－γ角度的旋轉矩陣。

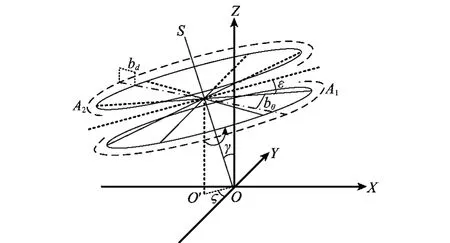
圖1 旋轉基線干涉儀系統偏差示意圖

對應的無模糊相位差為

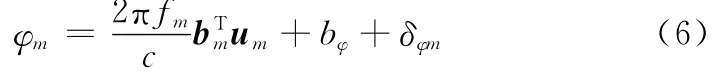
式中，um為第m次觀測時的單位視線列矢量，表示為

式中，xom為第m次觀測時，觀測站位置列矢量；xtm為第m次觀測時，目標位置列矢量。

根據上述模型，分析基線轉角偏差bθ和轉軸偏角 的關系。

定義基線的零角度指向與參考坐標系的零指向軸（如X軸）之間的偏角為基線轉角偏差bθ；轉軸偏離參考坐標軸Y軸的角為轉軸偏角 ；轉軸偏離參考坐標軸Z軸的角為轉軸傾角γ，如圖1所示。根據分析，命題描述如下：

命題1若基線轉角偏差bθ與轉軸偏角偏差 相等，在轉軸傾角γ為0時，兩者對基線指向矢量的影響相同；在轉軸傾角γ不為0且γ?π／4時，兩者對基線指向矢量的影響近似相同。

證明由式（2）和式（3）可得在各項系統偏差的影響下，基線的指向矢量變為

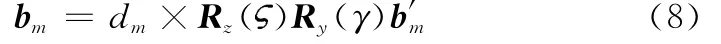
當γ較小且γ?π／4時，有sinγ≈0，cosγ≈1。式（8）可以化簡為

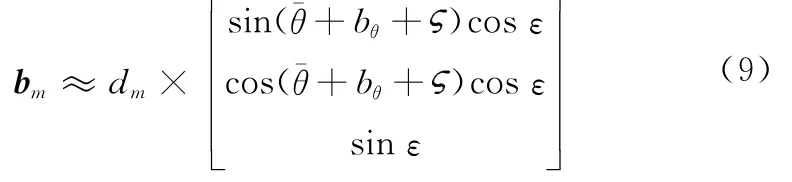
從式（9）可以看出，基線轉角偏差和轉軸偏角都通過改變基線指向矢量的X、Y坐標對其造成影響，并且若bθ＝ ，則兩個偏差造成的基線指向矢量偏差近似相等，當γ＝0，則等號可成立。

證畢

由命題1可知，由于基線轉角偏差bθ和轉軸偏角 具有等效性，若對基線轉角偏差和轉軸偏角進行聯合估計，其中一個量將會影響另外一個量的估計，因此兩者無法作為獨立估計量同時進行聯合估計。本文后面推導過程中，僅對基線轉角偏差bθ進行估計和校正。

2 偏差對定位精度的影響

由于非線性的影響，不同的系統偏差對定位結果造成不同的影響。下面分析各系統誤差對定位精度的影響。當基線長度大于輻射源半波長時，相位差會出現模糊，因此將M次觀測的相位差寫為矩陣形式，可得

高斯隨機誤差假設下的最大似然定位估計為

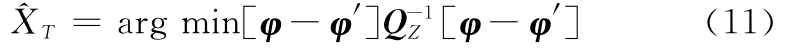
式中

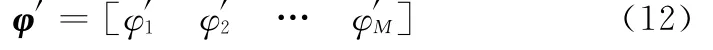
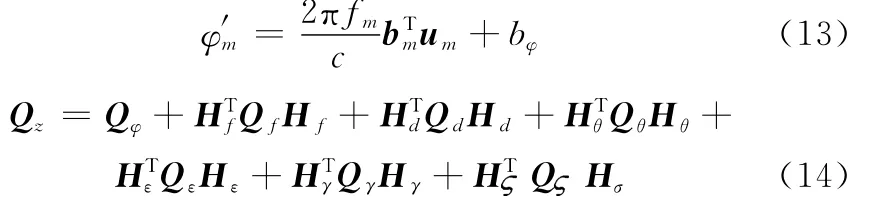
式中，Qz為不同種類的系統偏差等效成的相位差隨機誤差的協方差矩陣，其中Q表示各個量隨機誤差的協方差矩陣；H為φ′關于各個量的偏導數（雅克比矩陣，M×M方陣）。

式（14）中Hf為φ′關于載頻偏差的偏導數，表示為

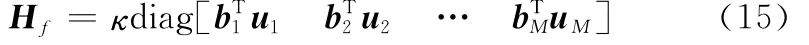
Hd為φ′關于基線長度偏差bd的偏導數，表示為

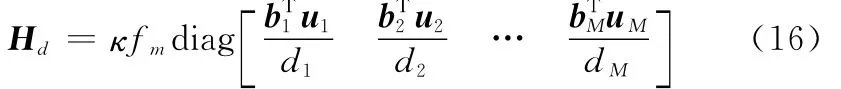
Hθ為φ′關于基線轉角偏差bθ的偏導數，表示為

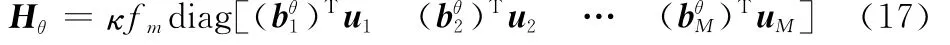
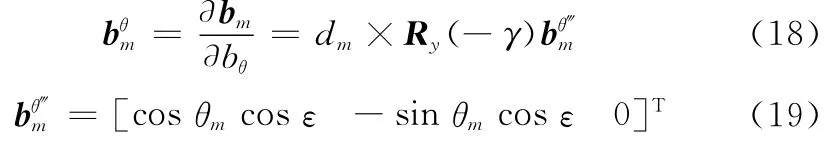
Hε為φ′關于基線垂直傾角ε的偏導數，表示為

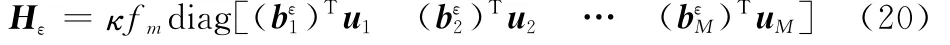
式中

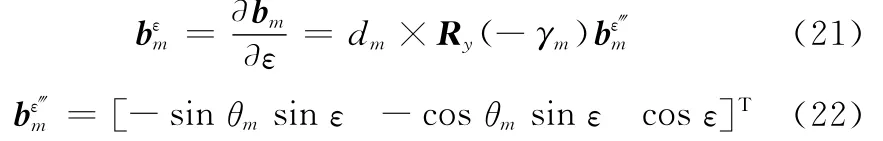
Hγ為φ′關于轉軸傾角γ的偏導數，表示為

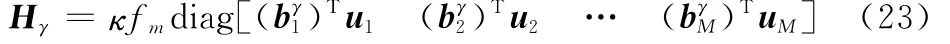
式中

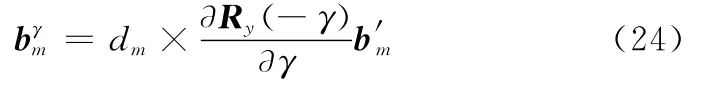
將式（11）化簡，可得

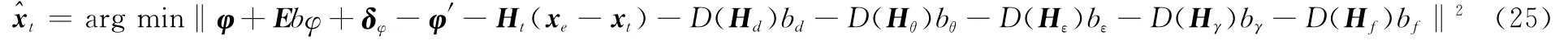
式中，E＝［1 1 … 1］M；δφ為相位差隨機誤差組成的行向量；xe為估計的目標位置列矢量；xt為目標真實位置列矢量；D（H）＝diag（H）表示取方陣H主對角線元素形成的列向量；Ht為φ′對目標位置的偏導數，表示為

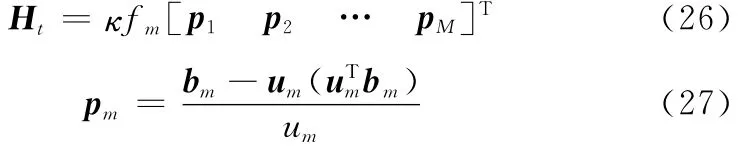
式中，um為目標與觀測站的距離。

因此，等效成的相位差系統誤差矢量為

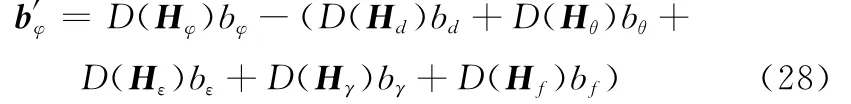
由隨機誤差引起的理論定位協方差矩陣為

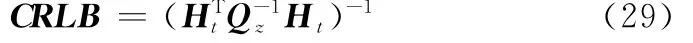
由系統誤差引起的定位偏差

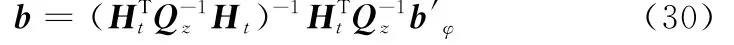
總的定位均方誤差為

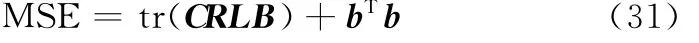
根據上述分析進行仿真實驗：觀測站位置［0 0 500］（單位：km），觀測站速度為［300 0 0］（單位：m），干涉儀旋轉周期為2s／r；目標輻射源載頻為3 GHz，重頻為100 Hz，基線長度為1.5 m；相位差隨機誤差為5°，累積時間為2 s，在充分考慮實際情況的條件下，設定各系統偏差分別為載頻系統偏差bf＝500 k Hz，相位差系統偏差bφ＝15°，基線長度系統偏差bd＝1 mm，基線轉角偏差bθ＝1.5°，基線傾角偏差ε＝1.5°，轉軸傾角γ＝1°。對不同俯仰角的目標進行了仿真，得到的各偏差引起的定位偏差如圖2所示。

圖2 各系統偏差對定位精度的影響

從圖2可以看出，部分系統偏差對定位結果的影響比較大，尤其是當俯仰角較小時，造成的定位偏差是無法接受的。在上述設定的場景中，引起定位偏差從大到小依次為轉軸傾角γ、基線轉角偏差bθ、基線傾角ε、基線長度偏差bd、載頻偏差bf、相位差系統偏差bφ。其中，相位差系統偏差bφ和載頻偏差bf引起的定位偏差極小，可以忽略不計。

因此本文在考慮上述場景的情況下，對轉軸傾角γ、基線轉角偏差bθ、基線傾角ε、基線長度bd這4項系統偏差進行聯合估計，消除引起的定位偏差。

3 系統偏差聯合估計方法

利用地面已知位置的單個或多個輻射源，可聯合估計出多種系統偏差［21］。基于標校站的系統偏差聯合估計法原理如圖3所示。

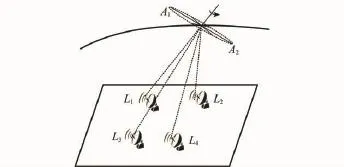
圖3 基于標校站系統偏差估計原理圖

首先考慮只有一個標校站，假設在一段時間內，觀測到M個信號。則將該標校站觀測到的相位差寫為矩陣形式為

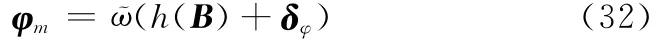
式中，系統偏差矢量為

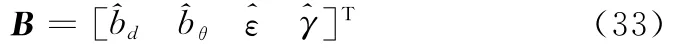
式（33）中，系統偏差矢量的元素個數根據需要聯合估計的偏差個數確定。

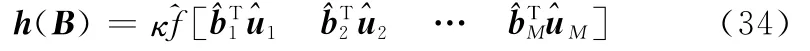
對于高斯白噪聲隨機誤差，由最大似然估計得

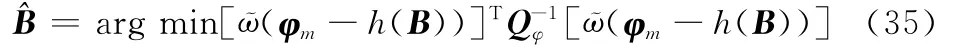
為了解模糊，可以通過提高標校源信號的發射功率從而降低觀測噪聲協方差，使得相位差系統偏差和隨機誤差引入的等效誤差小于π，即

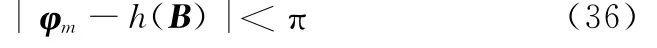
這樣，系統偏差估計問題可轉換為

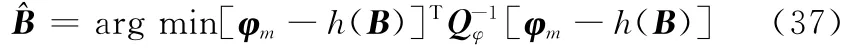
由最大似然估計得到的代價函數為

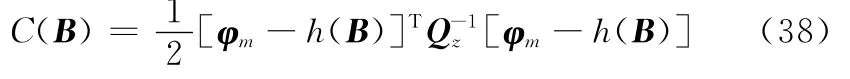
采用GN［25］算法迭代計算，獲得估計值為

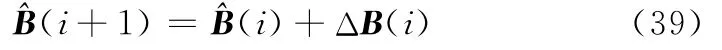
式中

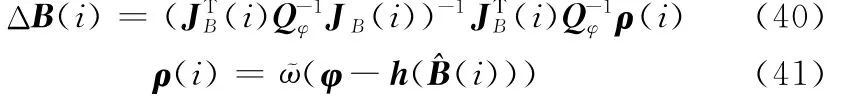
式中，Qφ為相位差隨機誤差協方差矩陣；JB為φ′關于各項系統偏差B的雅克比矩陣，表示為

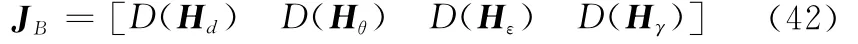
迭代結束條件為

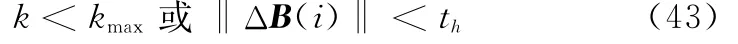
式中，k為當前迭代的次數；kmax為最大迭代次數；th為一個較小的門限值。

采用GN算法需要獲得估計值的初值，并且當其初值與真值相差很大時無法保證收斂，因此需要求得合理的初值。一種穩妥的方法是在各個偏差可能出現的最大值范圍內以一定的規律（如均勻分布）進行劃分［13］。得到的各個偏差劃分值進行遍歷組合，獲得多組估計的初值，如式（44）所示。

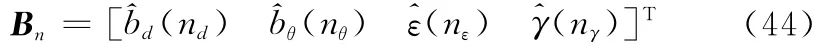
式中，n＝1，2，…，N，N＝NdNθNεNγ，Nd、Nθ、Nε、Nγ分別為各項系統偏差的劃分總數。然后對N組初值進行迭代，取代價最小的估計值作為最終的估計結果，表示為

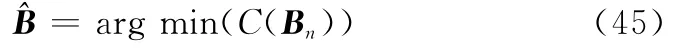
式中，C（Bn）如式（38）所示。

4 系統偏差聯合估計CRLB計算

CRLB等于Fisher矩陣的逆［20］，Fisher矩陣為

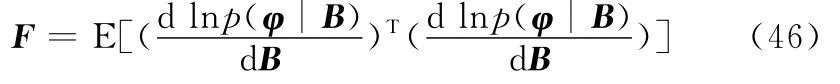
式中，p（φ｜B）為相位差φ關于B的條件概率密度函數。化簡式（46）可得

式中，σ2為相位差隨機誤差的方差；JB見式（42）。

由CRLB的定義，可得

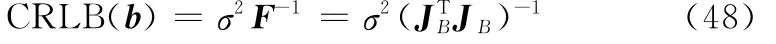
5 仿真分析

通過計算機仿真驗證該算法的有效性。仿真場景設定與第2節中設定的一致。

首先考慮單標校站的情況，將單標校站位置設定為［0 0 0］，采用上述方法，分別對以下兩組系統偏差進行其聯合估計的CRLB的計算：其中第1組為僅估計在上述場景中造成定位偏差最大的轉軸傾角γ、基線轉角偏差bθ、基線傾角ε3種系統偏差；第2組為在第1組的基礎上另加基線長度系統偏差bd。得到其CRLB如表1所示。

表1 單標校站聯合估計CRLB_

從表1中可以看出，當采用單標校站進行聯合估計時，如果僅僅估計轉軸傾角γ、基線轉角偏差bθ、基線傾角ε 3個偏差時，估計的CRLB較小，可以通過一定的方法對這3項系統偏差進行估計，但是如果估計項加入基線長度偏差bd時，則基線長度偏差bd的CRLB較大，無法估計。蒙特卡羅實驗次數5 000次，單標校站對轉軸傾角γ、基線轉角偏差bθ、基線傾角ε3個偏差進行聯合估計的結果如表2所示。

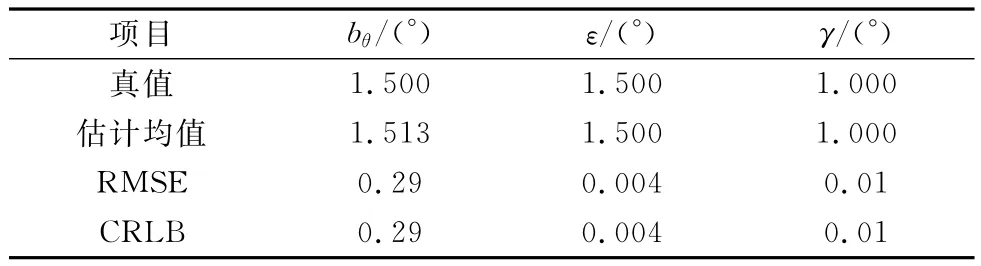
表2 單標校站系統偏差聯合估計結果

從表2可得如果僅估計轉軸傾角、基線轉角偏差和基線傾角偏差3個系統偏差，采用一個標校站就足夠了，但是如果要求對所有4個偏差進行聯合估計，則需要采用多標校站進行聯合估計。

為聯合估計4個系統偏差，設定兩個標校站，位置分別為［－400 0 0］（單位：km）、［400 0 0］（單位：km）。采用上述GN算法，對各個系統偏差進行聯合估計，蒙特卡羅實驗次數為5 000次，得到的估計結果如表3所示。

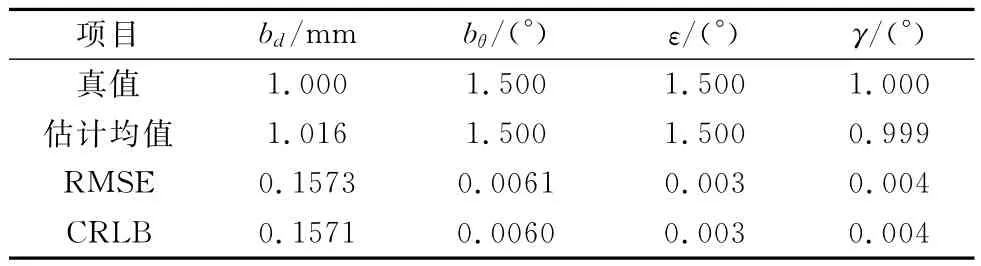
表3 雙標校站系統偏差聯合估計結果

從表3中可以看出，在此標校站場景下，本文采用的算法可以準確估計出各項系統偏差，并且估計的RMSE接近于CRLB。

然而，在實際的工程應用中，增加標校站的個數無疑會增大成本，因此有必要綜合衡量標校成本與定位精度改進效果的關系。以目標位置位于［350 350 0］（單位：km）為例，其他參數與之前一樣，根據式分別對表1中標校的兩組系統偏差進行計算，定位結果的RMSE如表4所示，其中第0組為不估計和標校任何系統偏差。

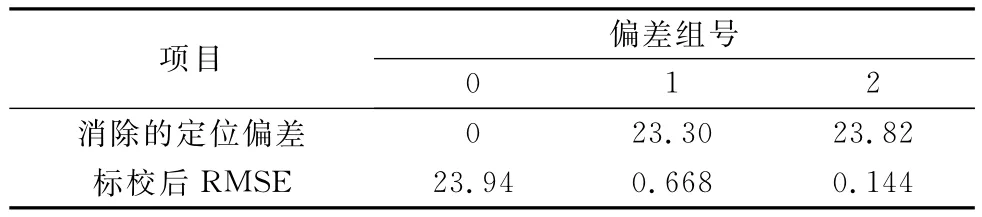
表4 標校系統偏差對定位精度的提高 km

從表4中可以看出，在此文設定的場景下，只估計并標校轉軸傾角γ、基線轉角偏差bθ、基線傾角ε3種系統偏差可以將定位的RMSE有效降低，多估計基線長度系統偏差bd，RMSE進一步減少，但是減少幅度不大，因此在對定位精度要求不是特別苛刻時，可以不估計基線長度偏差bd，以減少標校站個數，降低成本。

6 結 論

為了消除機械加工偏差以及安裝偏差造成RLBI多種系統偏差。本文首先建立了RLBI系統偏差的模型，然后分析了各系統偏差造成的定位偏差，找出了在本文場景下對定位精度影響顯著的4項系統偏差：轉軸傾角、基線轉角偏差、基線傾角、基線長度偏差。對此提出了一種基于標校站的系統誤差聯合估計法。仿真表明：單標校站可以有效估計出轉軸傾角、基線轉角偏差、基線傾角3類系統偏差；雙標校站可以有效估計出基線長度偏差、基線轉角偏差、基線傾角以及轉軸傾角4項系統偏差，并且其估計的RMSE接近于CRLB，驗證了該估計方法的有效性。

［1］Liu Z M.Direction-of-arrival estimation with time-varying arrays via Bayesian multitask learning［J］.IEEE Trans.on Vehicular Technology，2014，63（8）：3762- 3773.

［2］Liu Z M，Guo F C.Azimuth and elevation estimation with rotating long-baseline interfero-meters［J］.IEEE Trans.on Signal Processing，2015，63（9）：2405- 2419.

［3］Rose C M.Method for single satellite geolocation emitters using an ambiguous interferometry array［P］.United States of America，US 746365 9B1，2008.

［4］Kolanek J，Carlsen E.Precision geolocation system and method using a long baseline interfer ometer antenna system［P］.United States of America，US 7286085 B2，2007.

［5］Zheng J，Liu Z H，Jiang Q B，et al.Algorithm for passive localization with single observer based on ambiguous phase differences measured by rotating interferometer［C］∥Proc.of the IEEE 11th International Conference on Electronic Measurement &Instruments，2013：655- 659.

［6］Li T，Guo F C，Jiang W L.Multiple hypothesis NLSlocation al-gorithm based on ambiguous phase difference measured by a rotating interferometer［J］.Journal of Electronics&Information Technology，2012，34（4）：956- 962.（李騰，郭福成，姜文利.基于旋轉干涉儀模糊相位差的多假設NLS定位算法［J］.電子與信息學報，2012，34（4）：956- 962.）

［7］Fu S J，Vian J L，Grose D L.Determination of ground emitter location［J］.IEEE Aerospace and Electronics Systems Magazine，1998，3（12）：15- 18.

［8］Macphie R H，Tae H Y.On using the compound interferometer to obtain the power pattern of a conventional receiving array［J］.IEEE Trans.on Antennas and Propagation，2009，57（10）：3356- 3359.

［9］Macphie O H.Thinned coincident arrays for the direct measurement of the principal solution in radio astronomy［J］.IEEE Trans.on Antennas and Propagation，2003，51（4）：788- 793.

［10］Ballal T，Bleakley C J.Phase-difference ambiguity resolution for a single-frequency signal［J］.IEEE Signal Processing Letters，2008，15：853- 856.

［11］Ballal T，Bleakley C J.Phase-difference ambiguity resolution for a single-frequency signal in the near-field using a receiver triplet［J］.IEEE Trans.on Signal Processing，2010，58（11）：5920- 5926.

［12］Shieh C S，Lin C T.Direction of arrival estimation based on phase differences using neural fuzzy network［J］.IEEE Trans. on Antennas and Propagation，2000，48（7）：1115- 1124.

［13］Wei Z X，Cui W，Li F，et al.An ambiguity resovled correction algorithm of phase interfero meter based on Kalman prediction［C］∥Proc.of the IET International Radar Conference，2013：1- 5.

［14］Yun H L，Xiao D H，Bin T.A method for ambiguity solving based on rotary interferometer［C］∥Proc.of the International Conference on Communications，Circuits and Systems，2013：15- 17.

［15］Sheinvald J，Wax M.Direction finding with fewer receivers via time-varying preprocessing［J］.IEEE Trans.on Signal Processing，1999，47（1）：2- 9.

［16］Wu W，Cooper C C，Goodman N A.Switched-element direction finding［J］.IEEE Trans.on Aerospace Electronic Systems，2009，45（3）：1209- 1217.

［17］Sichun W，Inkol R，Rajan S，et al.An exact formula for the probability density of the phase error of a digital interferometer［C］∥Proc.of the 25th Communications on Biennial Symposium，2010：201- 204.

［18］Wen F Z，Li B，Chen D，et al.A phase consistency correction method of direction finding based on multi-channel interferometer receiver［J］.Electronic Warfare Technology，2012，27（2）：18 -23.（文富中，李波，陳嘟，等.多通道干涉儀測向的相位一致性校正方法［J］.電子信息對抗技術，2012，27（2）：18- 23.）

［19］Kleijn E，Vliet E M.Pustakhod D，et al.Amplitude and phase error correction algorithm for 3×3 MMI based machzehnder interferometers［J］.Lightwave Technology，2015，33（11）：2233- 2239.

［20］Xun Y，Cui Z Z.Two-dimensional circular array real-time phase interferometer algorithm and its correction［C］∥Proc.of the 2nd International Congress on Image and Signal Processing，2009：1- 5.

［21］Lu Z k，Jiang H，Gao Y，et al.Amplitude and phase errors selfcorrecting algorithm based on the uniform circular array［C］∥Proc. of the 2nd International Conference on Computer Science and Network Technology，2012：136- 140.

［22］Zhong D X，Yang Z B，Zhou Y Y，et al.Multi-source calibration for LBI direction finding and location system［J］.Systems Engineering and Electronics，2008，30（5）：960- 963.（鐘丹星，楊爭斌，周一宇，等.LBI測向定位系統的多標校源校正算法［J］.系統工程與電子技術，2008，30（5）：960- 963.）

［23］Li T，Guo F C，Jiang W L.Performance analysis of passive localization utilizing rotational Doppler-based single observer［J］.Journal of Astronautics，2010，31（10）：2388- 2394.（李騰，郭福成，姜文利.利用旋轉多普勒的單站無源定位性能分析［J］.宇航學報，2010，31（10）：2388- 2394.）

［24］Zhang M，Guo F C，Zhou Y Y，et al.A single moving observer auto-calibrated localization method using LBI［J］.Journal of Astronautica，2013，34（9）：1266- 1273.（張敏，郭福成，周一宇，等.運動單站長基線干涉儀自校正定位方法［J］.宇航學報，2013，34（9）：1266- 1273.）

［25］Kay S M.Fundamentals of statistical signal processing［M］.New Jersey：Prentice Hall，1998.

吳癸周（199-0- ），男，碩士研究生，主要研究方向為無源定位技術。

E-mail：13297498084＠163.com

張 敏（1984- ），男，講師，博士，主要研究方向為無源定位、信號處理技術。

E-mail：Zhangmin1984＠126.com

郭福成（1975- ），男，教授，博士，主要研究方向為無源定位、信號處理技術。

E-mail：gfcly＠21cn.com

Joint bias estimation method for rotating long baseline interferometer system

WU Gui-zhou，ZHANG Min，GUO Fu-cheng
（College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China）

Considering the effects of the amplitude／phase inconsistencies between different channels，the manufacture bias of the baseline and the installation bias of the baseline on the rotating long baseline interferometer（RLBI）location system，a mathematical model of these biases is proposed.The equivalent of the rotating baseline bias and the horizontal rotation shaft bias are proved.After that，the computing method of the theory localization error and the biases which may cause the distinct localization error is given.Finally，this paper proposes a joint Gauss-Newton bias estimation method based on calibration sources with known positions.The simulation indicates this method can achieve the Cramer-Rao lower bound（CRLB）and a single calibration source can improve the localization performance obviously.

interferometer；bias；estimation；rotating

TN 971

A

10.3969／j.issn.1001-506X.2015.11.05

1001-506X（2015）11-2454-06

2015- 02- 02；

2015- 05- 31；網絡優先出版日期：2015- 06- 18。

網絡優先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150618.0908.007.html

新技術研究高校合作基金（KX142600027）資助課題