小學數學解決問題策略研究

鄭三賢

策略方法的運用能增加學生成功的機會，使之有更多的積極體驗。掌握科學的學習方法和策略并在學習過程中加以運用的學生一般都有較高的自信心，因為他們擁有某種完成任務的手段。另外，方法和策略運用下的成功一般會導致高自信，因為成功是在學習者有效的控制下取得的，學生一般將之歸因于自己的能力，而不至于失去信心，所以，教學中教師要注重學法的指導，要重視學生思維方法的培養。下面結合本人的數學教學談談小學數學解決問題的相關策略。

一、比較策略

比較法是運用兩種或兩種以上的不同方面的典型事例進行比較。有比較，才有鑒別。因此，在教學中應有意識地創設比較辨析的思維情境，讓學生在比較辨析的思維情境中深化解題思路，發展思維品質。如，在教分數解決問題時，可將整數解決問題中的“倍數”，分數解決問題中的“分率”及分數除法中的“比”進行類比，幫助學生深刻理解算理。如：（1）學校圖書館，有科普書120本，是故事書的3倍。故事書有多少本？（2）學校圖書館，有科普書120本，是故事書的1.2倍。故事書有多少本？（3）學校圖書館，有科普書120本，是故事書的（1■）倍。故事書有多少本？（4）學校圖書館，有科普書120本，比故事書多（■）。故事書有多少本？（5）學校圖書館，有科普書120本，科普書與故事書的比是6：5。故事書有多少本？通過對上述題中的“倍數”、“分率”和“比”的比較，不僅有助于學生溝通知識與知識間的聯系，實現遷移，而且有利于學生異中求同，同中辨異，培養思維的深刻性。

二、猜想策略

亞里士多德說過：“思維是從疑問和驚奇開始的。”猜想質疑是放飛思維和想象的翅膀，學生有了疑問才會有進一步思考，才會有所發現，有所創造。猜想作為數學學習活動的一種，有著重要的價值。《標準》指出：“通過觀察、操作、猜想等方式，培養學生的探索意識。”為此，在教學中，教師要提供適當的猜想機會，營造一個寬容、自由、開放的心理環境，使學生想猜想和敢猜想。想猜想，就是學生對猜想充滿熱情、興趣和信心;敢猜想，就是不論猜想質量的高低，教師對學生的猜想充滿期望，扶持和激勵，使學生沒有精神壓力，沒有心理負擔，有自由發揮的機會，有無拘無束的思維空間。其次要營造一個猜想的知識環境，學會猜想。猜想不是信口開河、隨心所欲的盲目瞎猜，而要憑借自己的主觀愿望和知識背景，通過想象，估計和預測，大膽地提出問題的假設答案，而后對猜想的結果進行邏輯和實踐的驗證。如果猜想正確，就獲取了新知;如果猜想錯了就要轉換角度重新猜想，直至獲得成功。數學猜想能夠縮短解決問題的空間，獲得數學發現的機會，鍛煉數學的思維。

三、畫圖策略

著名的數學家斯蒂恩說過：“如果一個特定的問題可以轉化為一個圖形，那么，思路就整體地把握了問題，并且能創造性思考問題的解法。”因此，解決問題應該盡量利用直觀，達到化難為易，化抽象為形象，化靜態為動態的目的。

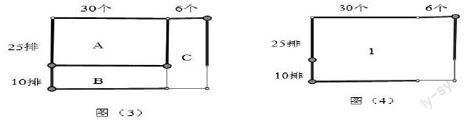
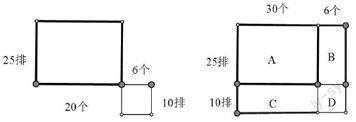
例如第六冊有一道練習題：“電影院原有座位25排，每排30個座位，擴建后增加10排，每排增加6個座位。擴建后可坐多少人？許多學生解成：30×25+6×10=810（人）。講評時，我引導學生：“你們看過電影嗎？電影院座位平面圖是怎樣的？你們能將這個列式畫成示意圖嗎？”在教師的啟發下，學生上臺將上式畫成示意圖（1），立即遭到同學們的異議，認為電影院的座位平面圖應當是方正，并上臺將圖（1）補成圖（2），說明擴建后可坐的人數=A+B+C+D。解法為：30×25+6×25+30×10+6×10=1260（人）

在圖（2）的啟發下，有一個學生說：“我還有更簡單的解法，只要將三部分的人數相加。”并上臺畫示意圖（3），并說明擴建后可坐的人數=A+B+C，列式為：30×25+30×10+6×（25+10）=1260（人）

接著在師生的共同探索下，有一個學生上臺畫了示意圖（4），說明擴建后可坐的人數=1。列式為：（30+6）×（25+10）=1260（人）

上面解決問題對于三年級學生來說，是一道抽象，不易理解的難題。但在教學中教師讓學生用“畫圖法”，不但使學生摒棄了錯誤解法，還引出了另外三種解法，選擇了最后一種最優解法，這樣在教師的引導下，同學們互相啟迪，在愉快的交流合作中理解了知識，提升了能力，受益終身。

四、假設策略

假設是一種常用的很重要的數學思維方法，對于有些問題按照一般方法很難解答時，可假設題中的情節發生了變化，假設題中兩個或幾個數量相等，假設題中某個數量增加了或減少了，然后在假設的基礎上推理，調整由于假設而引起變化的數量的大小，題中隱藏的數量關系就可能變得明顯，從而找到解題方法。這種解題方法就叫假設法。

五、動態策略

受客觀條件的限制，教材總是以靜態的形式呈現出來，而學生接受知識的過程卻是動態的。因此，針對學生接受知識的特點，我們要努力使數學教學成為活動的教學，轉化為豐富有趣的數學活動，讓學生感到數學學習實際上是一種愉快的探索活動。

解決問題策略的形成不是一蹴而就的，它是一個潛移默化的過程，需要較長時間逐步培養。培養學生的問題解決策略需要我們在長期的教學中創造地運用教材，充分利用學生身邊的數學素材，讓學生感知、探索和發現，在感知、探索和發現中來發展解決問題的策略。