儲油罐拱頂的應力分析與壁厚設計

何乾偉 付和銀（西南石油大學 石油與天然氣工程學院，四川 成都 610500）

李雨峰（西南石油大學 機電工程學院，四川 成都 610500）

近年來，由于工業和經濟的快速發展，世界各國對石油的需求量快速增加，儲油罐的數量也逐漸增加，拱頂罐由于具有制造簡單、建設成本低并且具有一定的承壓能力等優點而在工業中常被用到。拱頂罐在石油行業由于國家儲備、中轉需要等因素而被廣泛使用，但石油屬于易燃易爆產品，因此，合理的結構設計對儲油罐的安全運行和管理具有重要意義。

1 儲油罐拱頂的強度設計

本文所涉及的儲油罐結構如圖1。儲油罐頂蓋為球殼，拱頂球殼和罐壁的連接部分為環殼，罐壁為圓筒形狀，環殼與罐壁、環殼與拱頂球殼平滑連接。圖1為儲油罐的簡化模型。

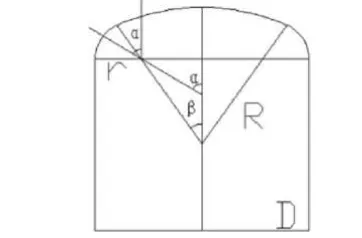
圖1 儲油罐的簡化模型

r：環殼第一曲率半徑 R：拱頂球殼半徑 D：罐壁直徑

1.1 為了簡化模型，對拱頂進行應力分析時做出如下假設：

1.1.1 不考慮施工和儲油罐的制造問題，假設儲油罐為一均勻的整體

1.1.2 不考慮拱頂球殼和環殼的自重，只是在儲油罐內壓大于外壓的條件下對其進行設計

1.1.3 環殼與罐壁、環殼與拱頂球殼連接絕對平滑

1.2 設計思路：

1.2.1 根據儲油罐的直徑，通過等強度原則設計拱頂球殼半徑

1.2.2 通過分析拱頂球殼和環殼的應力，找出整個罐頂最大應力值，根據最大應力確定整個罐頂的壁厚

1.3 設計步驟：

1.3.1 當整個儲油罐內壓力均為P時，拱頂球殼上任意一點在與球殼相切的任意方向上，應

力值均為σ=PR/(2δ)。對罐壁而言，最大應力出現在罐壁環向，其值為

σ=PD/(2δ)。根據等強度設計原則，R=D時，即是儲油罐的拱頂球殼半徑與罐壁

的直徑相同時，相同壁厚的拱頂球殼和罐壁最大應力值相同，在工程設計中一般取

R=（0.8-1.2）D，在本文以下的分析中，均采取R=D做計算。

1.3.2 對于拱頂球殼，其最大應力值為σ=PD/(2δ)

1.3.3 環殼應力狀態較復雜，其應力計算步驟如下：

1.3.3.2 第一曲率半徑：

第二曲率半徑：

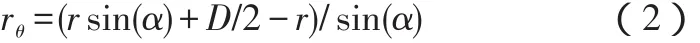
1.3.3.3 經向應力求解

在計算點處（α角與環殼的交點），y方向上內壓對拱頂球殼和環殼的力之和等于計算點下方環殼對上方環殼的拉力：

1.3.3.4 根據體素平衡方程計算環殼環向應力：

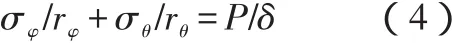
4通過（1）-（4）逐步化簡得到環殼的經向應力值和環向應力環：

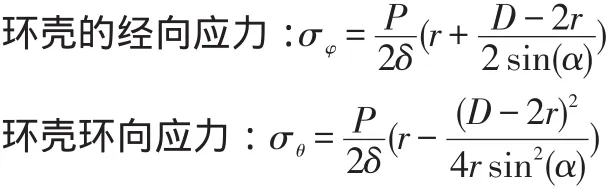
由上式可知，在相同的α角的條件下，環殼的經向應力大于環殼環向應力，所以環殼的設計應力應選經向應力。經向應力隨著α角的變化而變化，當si（nα）最小時經向應力達到最大值。

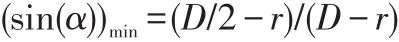
所以 (σφ)max=PD/2δ

由此可見，環殼的最大應力值和灌頂的最大應力值相同

所以其設計壁厚:

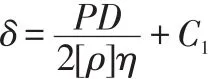
δ：罐頂壁厚 α：計算點處環殼半徑與豎直方向夾角。[ρ]許用應力η：焊縫系數 C1：腐蝕裕量

1.4 實例計算：

已知：儲油罐直徑為20m，內壓為0.5MPa，罐頂材料許用應力值為400MPa，罐頂的焊縫系數為0.85，腐蝕裕量為0.5mm。

由計算得δ=15.2mm

2 結語

儲油罐的拱頂球殼設計應力分析較為容易，而環殼的設計應力分析較為復雜，但是計算結果表明，儲油罐在滿足文中所述的條件時，無論環殼的第一曲率半徑如何，其應力值總是小于拱頂球殼的應力值，并且只有在環殼和拱頂球殼的接觸處，環殼應力值才達到最大，并且與拱頂球殼的應力值相同，這樣會避免因應力突變而產生的應力集中現象，但其缺點在于環殼和罐壁的接觸處因應力值的不同而存在應力集中現象，因此在進行這類儲油罐的設計時應考慮到這一點。

[1]王輝.10×10^4m3大型浮頂油罐的設計[J].石油化工設計,2012,29(2):9-12.

[2]帥健,于桂杰.罐道及儲油罐強度設計[M].北京:石油工業出版社,2006:174-237.