溫度對鐵電薄膜極化反轉的影響

韓志友

(大慶師范學院 機電工程學院，黑龍江 大慶163712)

0 引言

鐵電薄膜的極化反轉長期以來是一個熱點課題，因為它可能為將來的納米電子存貯器及邏輯裝置提供可觀的途徑［1］。在實驗上和理論上，有很多關于鐵電薄膜的極化反轉特性的報道。實驗上，Mitoseriu等人［2］研究了室溫下不同尺寸的BaTiO3鐵電陶瓷的極化反轉特性。結果表明隨著尺寸的減小反轉時間也隨之減小。Yanase［3］等人利用兩步沉積技術觀察了異質外延BaTiO3薄膜的尺寸效應。即使鐵電薄膜厚度減小到12 nm 時，在異質外延BaTiO3中仍可清楚地觀察到鐵電電滯回線。人們也建立了一些理論模型來研究鐵電薄膜極化反轉行為，例如Avrami 理論［4］，Kolmogorov－ Avrami –Ishibashi (KAI)理論［5］，non－KAI 模型［6］，and 基于Landau－type 自由能不連續模型等［7］。

在上述理論中，沒有考慮鐵電薄膜極化反轉的表面效應。近年來，Ong 課題組通過在Tilley－Zeks 模型中引入Landau－Khalatnikov 運動學方程來研究鐵電薄膜的極化反轉特性。［8－9］。Cui 課題組通過在鐵電薄膜中引入表面過渡層，并結合Landau－Khalatnikov 運動學方程來研究鐵電薄膜的極化反轉特性。此方法更加接近鐵電薄膜的實際結構［10］。

本文沿用Cui 等人的思想，研究溫度對鐵電薄膜極化反轉特性的影響。到目前為止，此研究未見文獻報道。

1 模型和理論

如圖1所示，含有表面過渡層的鐵電薄膜夾持在兩金屬電極間，并且認為薄膜是由薄層堆垛而成。在平行于薄膜表面的每層性質均勻，薄膜性質只沿z 方向變化。每一薄層厚度為Δz，整個薄膜層數為N層。所以鐵電薄膜總厚度為L=NΔz。如果起點位于左邊表面，此時z=0 那么任意層在z 的位置可以用i 來標記，即z=iΔz(1 ≤i ≤N)。

為了研究考慮兩鐵電層間的界面耦合的雙層膜系統，需要建立合適的Landau 型自由能表達式。根據文獻［10］，我們在Landau 型自由能表達式中引入每一層極化的二次冪，并假設它的系數是位置的函數，以為反映每個鐵電層表面過渡層的貢獻。因此，鐵電薄膜的的自由能表達式可以表示為［10］

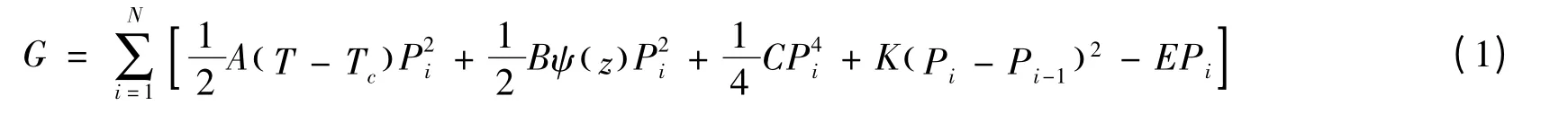
在z=0 與L 處的邊界條件為［10］

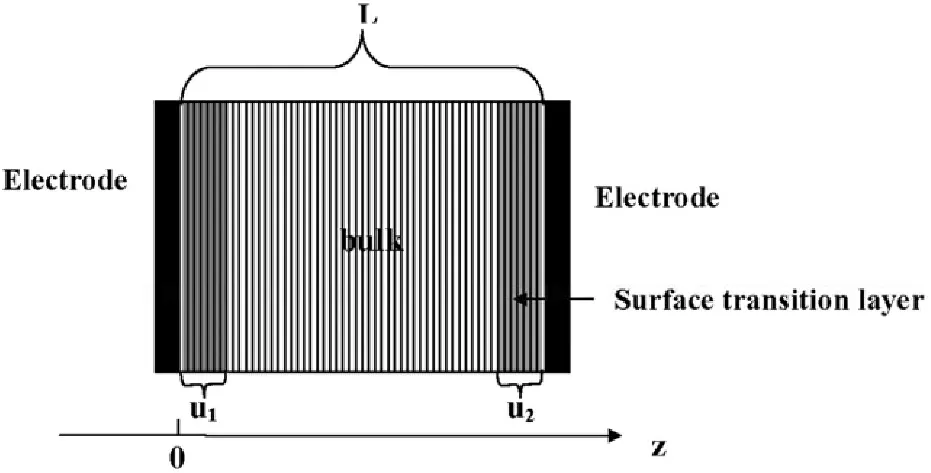
圖1 鐵電薄膜結構

這里Pi是薄膜中第i 層的極化;系數A，B，C，與K 是正值并且不依賴與溫度T 和位置z;Tc是鐵電層體材料的相變溫度;E 是局域電場。方程(2)中的第二項反映了鐵電層表面過渡層的作用。分布函數ψ(z)反映了表面效應。K(Pi－ Pi－1)2這一項表示相鄰層間的耦合效應。極化梯度( dP/dz)2這項已經包括在有限差分表達式K (Pi－ Pi－1)2中［11］。

The time variation of the polarization during switching can be described by the Landau－Khalatnikov equation as follows:

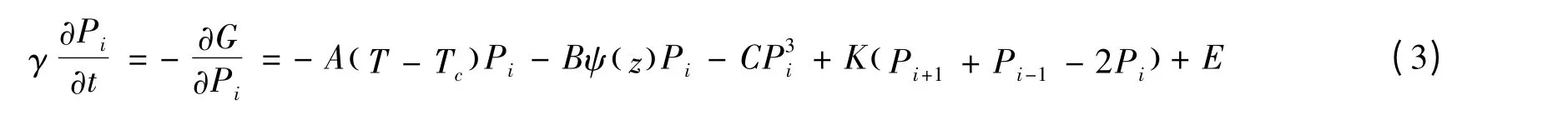
這里γ 是粘滯系數，它會引起疇運動的延遲。

為方便計算我們將物理量進行重整化使其成為無量綱參量。我們設fi=Pi/P0其中tT=T/Tc，δ=B/B0其中B0=ATc，ζ=z/ξ0其中σ=(ε0ATc)－1，e=E/E0其中E0=P0/ε0，這里ε0為真空介電常數。最后我們得到重整化后的方程為:

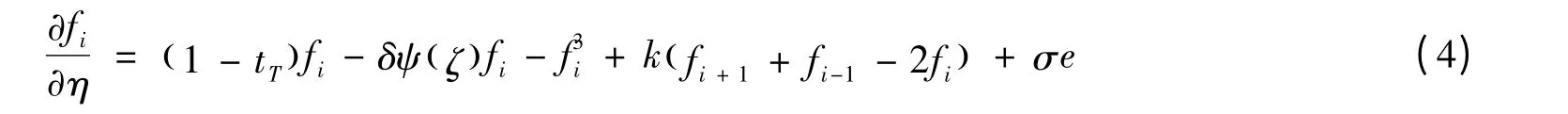
相應重整化后的邊界條件為

我們引入j 來標記離散時間η=jΔη。則鐵電層中每一層極化對時間的依賴關系表示為fi，j。通過對方程(4)左邊時間的向前差分，得到對fi，j的差分方程為:

根據微分(df/dζ )的二次小量有限差分，方程(5)可寫為

整個薄膜的極化為

反轉電流為

由于實驗上沒有關于表面過渡層影響的實驗數據，所以我們選取簡單的分布函數形式。分布函數形式的選取不會影響我們計算結果與得到的結論［10］。

其中u1與u2分別是層左邊與右邊表面過渡層的厚度。參量λ1(λ2)分別反映了左右表面附近鐵電層的自由能密度的變化強度。為簡單方便，我們假定鐵電層的兩個表面過渡層是對稱的，即u=u1=u2，λ=λ1=λ2。

我們規定，鐵電薄膜極化的初始狀態為負的剩余極化，即初始極化為零電場情況。

2 結果及討論

圖2給出了鐵電薄膜的平均極化隨時間的演化關系曲線。圖中三條曲線的共同趨勢是隨著時間的增加，平均極化發生反轉，然后達到飽和平衡值。平均極化的初始值和結束值都隨著溫度的增加而減小。可以清楚地看到，曲線沿著時間軸向左移動，表明溫度高時會加快極化反轉。并且，隨著溫度的增加飽和平均極化減小，上述的結果很好地符合Zhang 等人實驗上所觀察到的結果［12］。

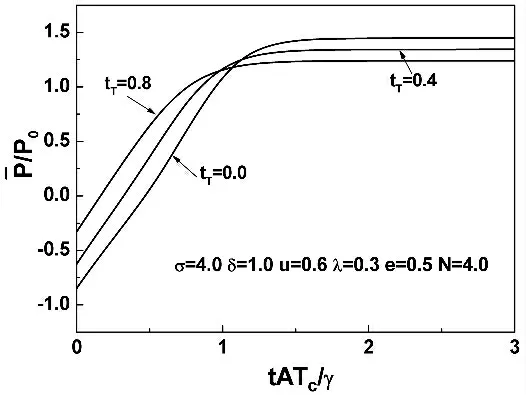
圖2 不同溫度下，平均極化隨時間的變化

圖3描述了不同溫度下，鐵電薄膜的反轉極化隨時間的變化關系。溫度一定，隨時間增加，反轉電流出現峰值。峰值對應著此時極化發生反轉。隨溫度的增加，反轉電流的峰值降低，并沿時間軸向左側移動。說明，隨著溫度的增加，極化減小，極化反轉的時間縮短。

圖3 不同溫度下，反轉電流隨時間的變化

3 結語

利用Landau－ Khalatnikov 運動學方程，我們討論了溫度對含有表面過渡層的鐵電薄膜極化和反轉電流的影響。得到結果如下:(1)隨著溫度降低，鐵電薄膜的極化增大，反轉電流的峰值增大;(2)溫度增高可加快鐵電薄膜極化的反轉。

［1］Xiaohui Liu，Yong Wang，Pavel V.Lukashev，J.D.Burton，and Evgeny Y.Tsymbal.Interface dipole effect on thin film ferroelectric stability:First－principles and phenomenological modeling［J］.Phys.Rev.B 2012，85:125407.

［2］Liliana Mitoseriu，Dan Ricinschi，Catalin Harnagea，Masanori Okuyama，Takeyo Tsukamoto and Vasile Tura.Grain size dependence of switching properties of ferroelectric BaTiO3ceramics［J］.Jan.J.Appl.Phys.1996，35(9B):5210－5216.

［3］Naoko Yanase，Kazuhide Abe，Noburu Fukushima and Takashi Kawakubo，Thickness Dependence of Ferroelectricity in Heteroepitaxial BaTiO3Thin Film Capacitors［J］.Jan.J.Appl.Phys.1999，38:5305.

［4］Eng－Kiang Tan，J.Osman，and D.R.Tilley.Theory of switching in bulk first－order ferroelectric materials［J］.Phys.Stat.Sol.(b)2001，228(3):765－776.

［5］Ahmad M.Musleh，Lye－Hock Ong，and D.R.Tilley.Effects of extrapolation length _on switching time and coercive field［J］.J.Appl.Phys.2009，105:061602.

［6］Alexander K.Tagantsev，Igor Stolichnov，Nava SetterJeffrey S.Cross and Mineharu Tsukada，Non－Kolmogorov –Avrami switching kinetics in ferroelectric thin films［J］.Phys.Rev.B 2002，66(21):214109.

［7］Vasile Tura，Dan Ricinschi，Liliana Mitoseriu et al，Simulation of switching properties of ferroelectric on the basis of dipole lattice model［J］.Jan.J.Appl.Phys.1997，36:2183.

［8］Lye－Hock Ong and Ahmad Musleh，Tilley－Zeks Model in Switching Phenomena of Ferroelectric Films［J］.Ferroelectrics.2009，380:150.

［9］Ahmad Musleh Alrub and Lye－ Hock Ong，Curie temperature and critical thickness of ferroelectric thin films［J］.J.Appl.Phys.2011，109:084109.

［10］Lian Cui，Quan Xu，Yunfeng Dong，Zhiyou Han，Huijie Xue，Tianquan Lü.Influence of surface transition layer on switching time and coercive field of a ferroelectric thin film［J］.Solid State Science，2013，16:65－70.

［11］Veng Cheong Lo，Simulation of thickness effect in thin ferroelectric films using Landau–Khalatnikov theory［J］.J.Appl.Phys.2003，94:3353.

［12］Y.Zhang，X.L.Zhong，Z.H.Chen，J.B.Wangand Y.C.Zhou，Temperature dependence of polarization switching properties of Bi3.15Nd0.85Ti3O12ferroelectric thin film［J］.J.Appl.Phys.2011，110:014102.