一類相對轉動系統的復雜運動及時滯速度反饋控制

尚慧琳，李偉陽，韓元波，文永蓬

（1．上海應用技術學院機械工程學院，上海 200235；2．上海工程技術大學城市軌道交通學院，上海 201620）

一類相對轉動系統的復雜運動及時滯速度反饋控制

尚慧琳1，李偉陽1，韓元波1，文永蓬2

（1．上海應用技術學院機械工程學院，上海 200235；2．上海工程技術大學城市軌道交通學院，上海 201620）

研究一類典型的相對轉動系統的系統參數引起的復雜運動（如混沌運動和安全域侵蝕），并對系統施加時滯速度反饋來控制系統的這些復雜動力學行為，從而保障系統的振動可靠性。利用Melnikov函數法獲得時滯速度反饋控制相對轉動系統產生混沌和安全域分岔的臨界激勵；并數值模擬了系統在不同控制參數條件下的動力學行為，從而驗證了理論分析的正確性。研究結果表明，在正的反饋增益系數下，時滯速度反饋能夠有效地用于控制相對轉動系統的混沌運動和安全域侵蝕。

相對轉動系統；Melnikov函數；時滯速度反饋；混沌；安全域

轉動是最常見的能量傳輸方式之一，轉動機械廣泛應用于機械加工制造，動力傳遞等領域。相對轉動是轉動機械系統中普遍存在的動力學現象，相對轉動系統的復雜振動會影響設備的平穩運行，甚至導致系統構件破壞的嚴重后果，因此，相對轉動系統中的振動問題受到學術界的廣泛關注。趙武等［1］研究了一類非線性相對轉動周期系統的平衡穩定性問題，將非線性的相對轉動系統扭振問題的運動穩定性分析轉化為一類周期性變系數常微分方程解的穩定性。劉爽等［2］研究一類時滯非線性相對轉動系統，發現時滯的改變能夠引起系統的Hopf分岔，從而對系統動力學行為帶來定性影響。劉浩然等［3］建立了具有時變剛度、非線性阻尼和諧波激勵的類相對轉動時滯非線性動力系統的動力學方程。張文明等［4］研究了一類非線性相對轉動系統的混沌運動及多時滯反饋控制，發現通過減小或者增大多時滯反饋參數，能有效地將系統的混沌運動控制到單周期運動。喬杰敏等［5］建立了具有廣義阻尼力和非線性恢復力的二端面相對轉動系統的模型與一類兩質量相對轉動系統的統一的非線性動力學模型，給出系統發生混沌運動的必要條件，并利用數值仿真進一步研究了系統的混沌運動。目前相對轉動系統的研究主要集中在關于模型、穩定性、周期解等系統特性的分析，而對于相對轉動系統的全局分岔和混沌等方面的研究的相關報道相對較少［6］。因此研究相對轉動系統中系統參數引起的混沌運動機制并提出控制方法成為本文的研究目的之一。

相對轉動系統的混沌振動雖然會引起不規則的輸出響應，并加劇了傳動軸本身的疲勞失效，仍是系統結構的剛度范圍內的動力學行為。然而系統的振動幅度過大卻往往會直接引起系統結構的強度問題，如造成傳動軸的破壞。研究相對轉動系統的振動的有界性問題，特別是安全域侵蝕問題，具有非常重要的工程實際意義。安全域這個概念最早是在Thompson等［8］在研究船舶在波浪作用下的傾覆問題時提出的，它被定義為所有有界解吸引域的集合。安全域侵蝕就意味著安全域邊界分形，常常用來解釋工程結構的振動對初始條件的敏感性［9－10］。關于相對轉動系統的振動有界性和安全域侵蝕問題的控制研究目前報道極少。因此本文的另一個研究目的就是揭示一類相對轉動系統的安全域侵蝕機理并實施控制。為此，本文提出利用線性時滯速度反饋來控制相對轉動系統的安全域侵蝕現象。因為時滯反饋不但是控制混沌的重要手段［11－12］，而且已有許多研究表明它是控制安全域侵蝕的良好策略。如Alsaleem等利用時滯位置反饋控制了靜電驅動微加速度計振動系統的安全域侵蝕現象，從而有效地抑制了系統微結構的吸合不穩定。筆者通過對Duffing系統、Holmes-Duffing系統和一類單自由度參數激勵系統［13－16］施加時滯反饋控制均發現，時滯反饋控制能夠有效控制系統的安全域侵蝕。這些為利用時滯速度反饋控制相對轉動系統的安全域侵蝕提供了可能性。

本文考慮一類典型的相對轉動系統，研究系統的復雜運動如混沌運動和安全域侵蝕的機制，并利用時滯速度反饋對系統的復雜動力學行為實施控制。

1 模型及無擾動分析

本文以一類兩質量相對轉動系統為研究對象，對系統引入時滯相對速度反饋控制，其簡化模型見圖1，圖1中θ1和θ2為集中質量的扭轉角，J1和J2為相對轉動系統集中質量的轉動慣量，和為系統集中質量的角速度為時滯速度反饋控制項，式中t－τ時刻兩質量傳動系統的相對角速度，q為反饋增益系數，τ為時滯量。將時滯相對速度反饋控制項當成廣義力，可對系統建立有耗散項的廣義拉格朗日方程

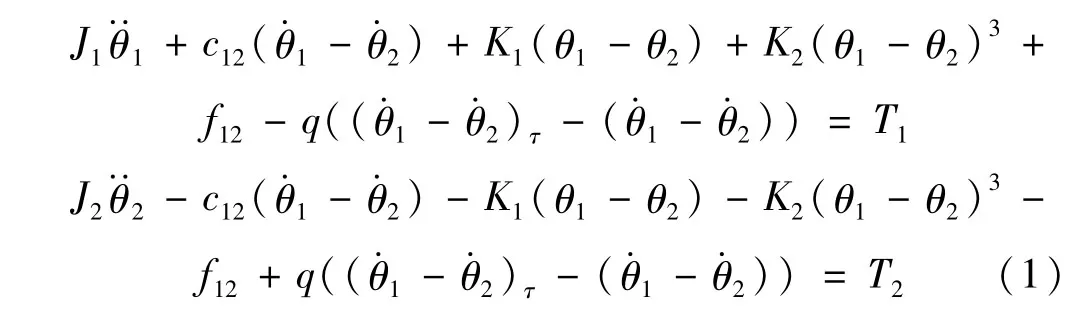
式中：K1為線性剛度，K2為非線性剛度，c12為線性阻尼系數，T1和T2為外部施加扭矩，f12為非線性粘滑摩擦力

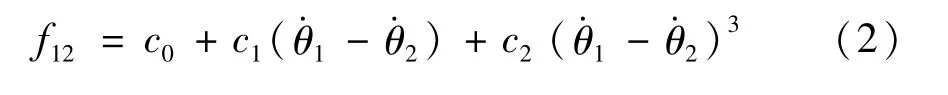
式中：c0，c1和c2分別為靜摩擦常數，線性和三次非線性阻尼系數。由于工程中動力傳動系統的扭矩通常是簡諧激勵，因此可設

令ψ1＝θ1－θ2，線性變換式（1）即可得到時滯速度反饋相對轉動系統

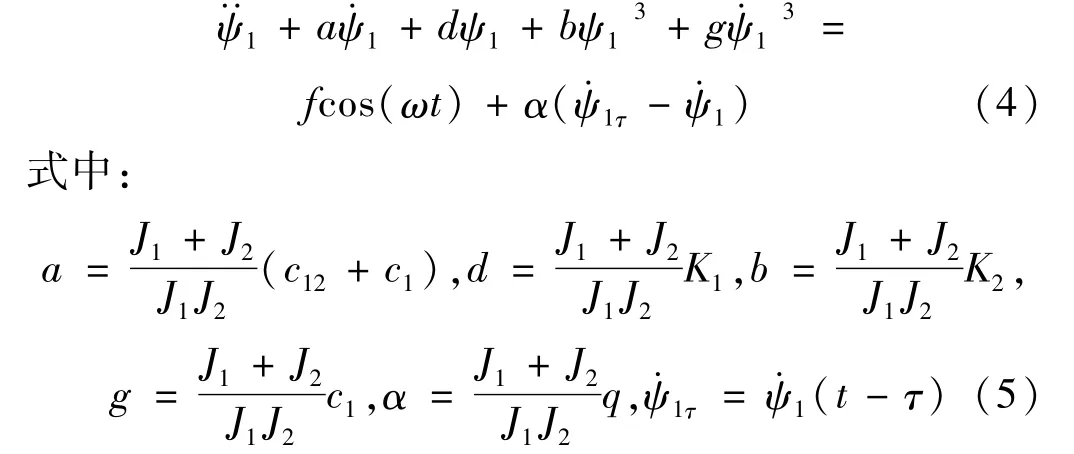
當τ＝0時，時滯速度反饋項α（ψ·1τ－ψ·1）＝0，式（4）退化為無控制的相對轉動系統

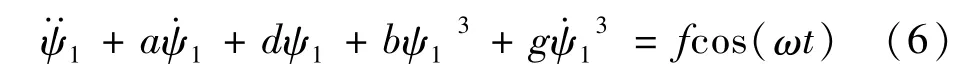
式中：a是Coulomb干摩擦力項的系數，滿足a＞0；系數b與軟彈簧非線性剛度K2成正比，有b＜0；線性剛度相關系數d＞0，且三次非線性阻尼相關系數g＞0［17］。式（4）相當于對相對轉動式（6）施加了單通道的線性時滯速度反饋α（ψ·1τ－ψ·1）的控制系統，其中控制參數有兩個，α為反饋增益系數，根據式（5），與施加在式（1）中的反饋增益系數成正比；τ為時滯量，與式（1）中時滯量一致。

為了考察式（3）的Hamilton系統及其同宿軌道，考慮式（3）的非保守項為弱擾動，將阻尼、外激勵及反饋增益在小參數ε作用下重新標度。設

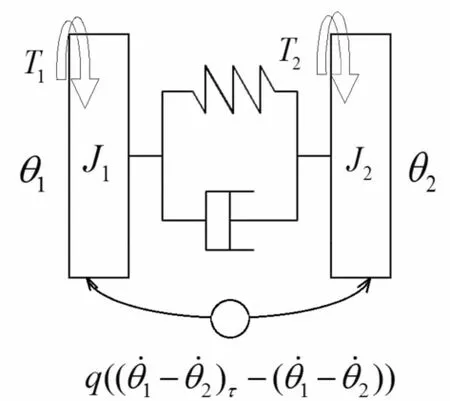
圖1 一類時滯速度反饋控制相對轉動系統的簡化模型Fig．1 The simplified model of a relative rotation system with the delayed velocity feedback

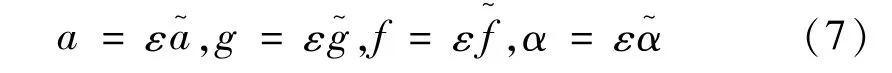
式中：a～＝O（1），g～＝O（1），f～＝O（1），α～＝O（1）．則式（4）可表示為：

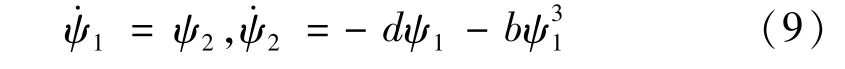
其Hamilton函數為：

顯然，當ε＝0時，式（8）退化為無擾系統

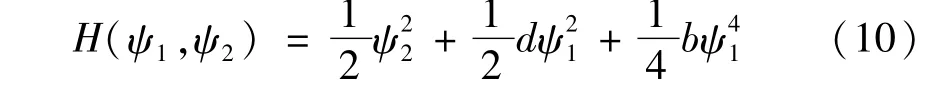
2 全局分岔條件

首先將Melnikov函數法應用到無控制的相對轉動式（6），從而得到系統發生全局分岔的必要條件。由式（8）和式（11），式（6）的Melnikov函數可表示為

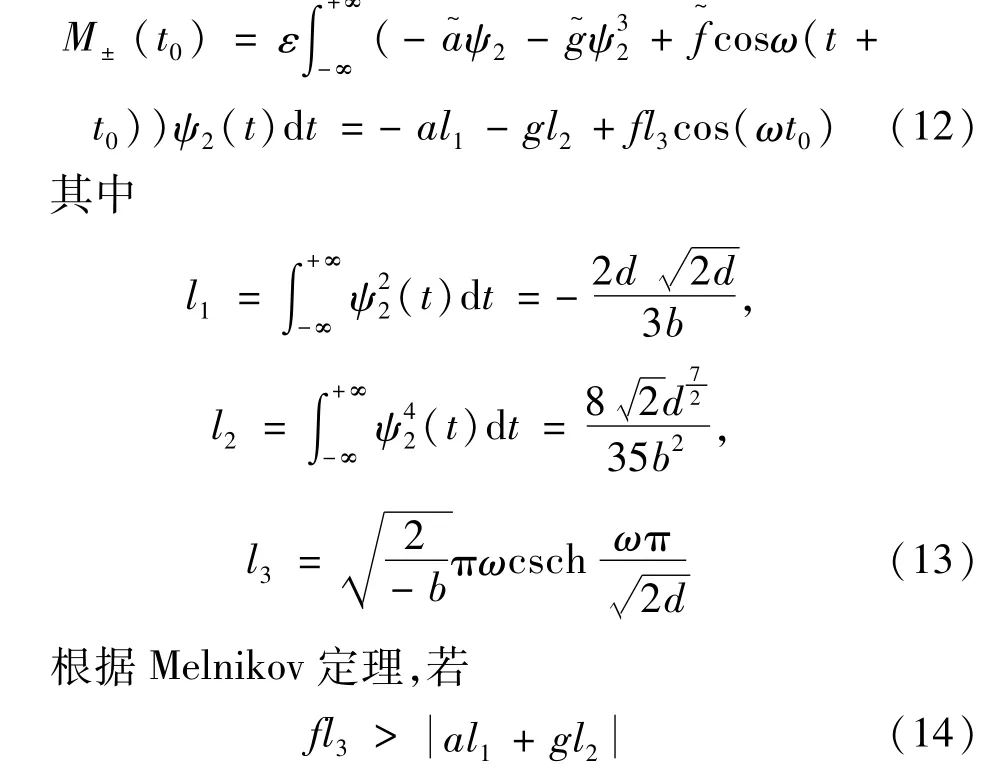
則存在某t0使得M±（t0）＝0，且M±（t0）′≠0。由此可知式（12）存在簡單零點。這就意味著穩定流形和不穩定流形在Poincaré截面上橫截相交，同宿軌線破裂，從而導致Smale馬蹄意義下的混沌運動和系統的安全域侵蝕。因此，當

會引起系統的混沌運動和安全域分形侵蝕，其中f0則為式（6）同宿分岔的激勵振幅閾值。

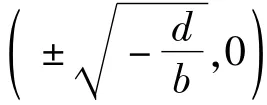
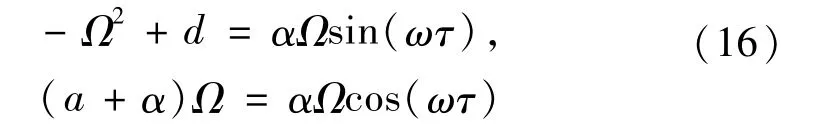
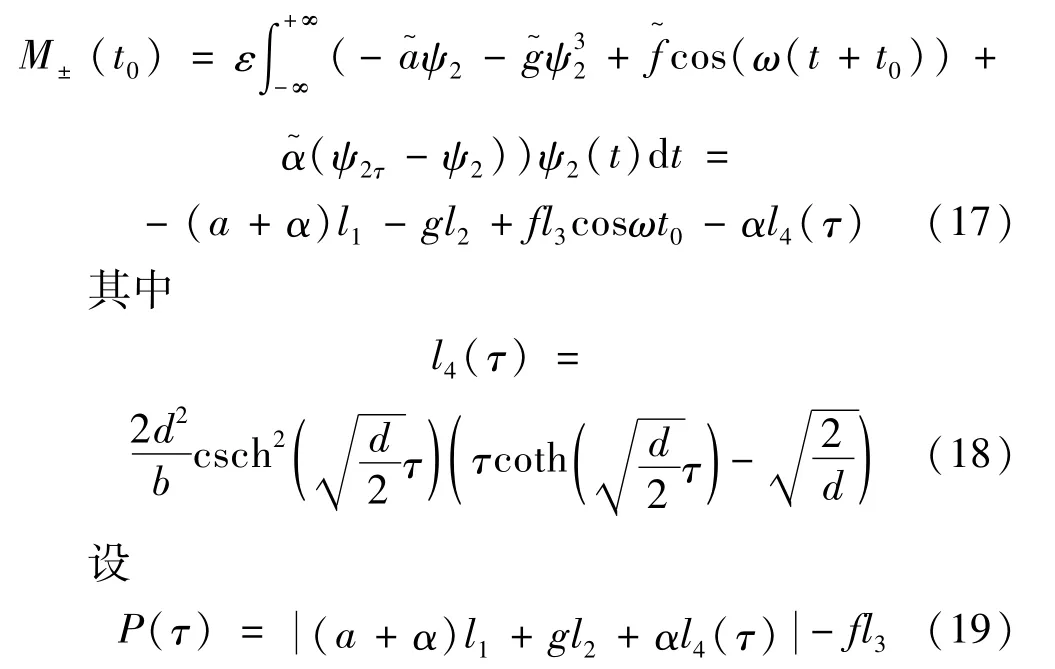
則根據Melnikov定理，當P（τ）＜0時式（17）存在簡單零點，式（4）會發生同宿分岔。相反地，當P（τ）＞0時，有

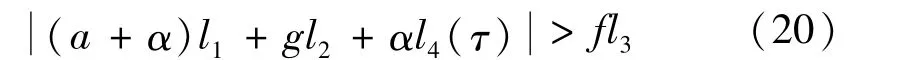
此時系統不發生同宿分岔，因此混沌運動和安全域侵蝕得以抑制。由此可以得到式（4）安全域侵蝕和混沌運動的激勵振幅門檻值

當τ＞0時，有l4（τ）＞0，這說明增益系數大于零時，fτ＞f0，反饋控制下引起安全域侵蝕和混沌運動的激勵振幅門檻值得以提高。

將式（4）的參數取值定為

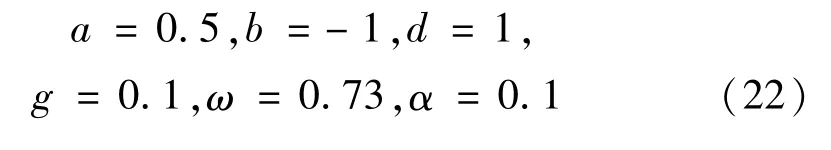
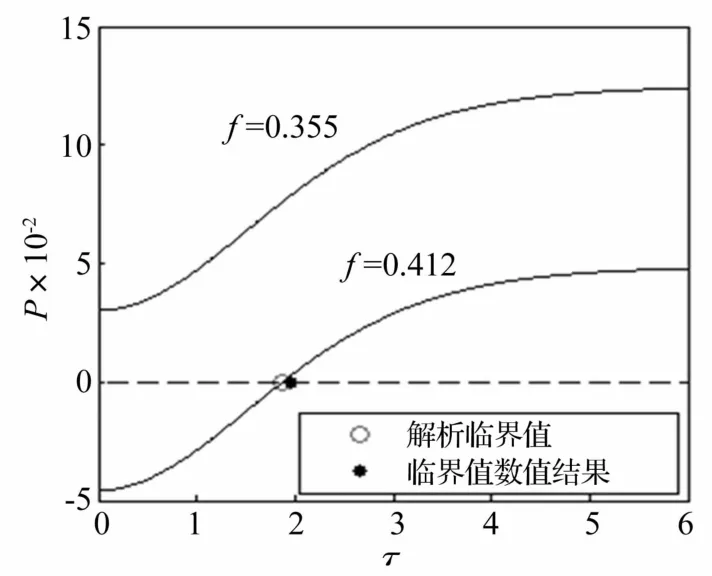
圖2 α＝0．1時不同激勵振幅下P（τ）隨時滯的變化Fig．2 Variation of P（τ）with time delay under different values of excitation amplitude whenα＝0．1

則不同激勵下P（τ）隨時滯的變化（見圖2）。根據圖2，f＝0．355時，在正的反饋增益下，無論有無時滯速度反饋控制，式（6）均不發生同宿分岔；而當f＝0．412，τ＝0時P（τ）＜0，說明式（6）發生同宿分岔；但P（τ）會隨著時滯量的增大，特別是當τ≥1．88時，有P（τ）＞0，這說明式（4）的同宿分岔得到抑制。由此可見，在正的反饋增益下，時滯速度反饋可以抑制相對轉動系統的混沌運動和安全域侵蝕。

3 數值仿真

3.1 混沌的產生及其控制

以2／ω頻率截取Poincaré截面，獲得相應參數下系統變化的數值仿真分岔圖，從而研究系統動力學行為隨參數的演變無控制情況下相對轉動式（6）隨外激勵f的分岔情況見圖3。由圖3可知，隨著外激勵f的增大，式（6）的動力學行為從周期運動經倍周期分岔最終走向混沌運動，與上一節的理論預測相吻合；當外激勵振幅f＝0．412時，式（6）會出現混沌運動，這一點由該參數條件下系統時間歷程圖和頻譜圖證實（見圖4）。

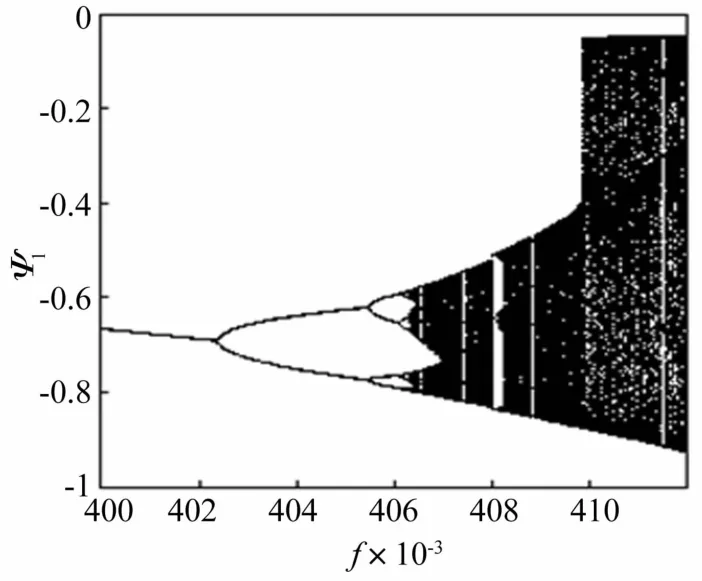
圖3 無控制系統（6）的激勵振幅分岔圖Fig．3 Bifurcation diagram of theexcitation of the uncontrolled system（6）

對于時滯速度反饋系統式（4），給定外激勵f＝0．412并給定時滯量，系統動力學行為隨增益系數的演變（見圖5）。此時，由圖4可知，當時滯量τ＝0時，式（4）會發生混沌運動。根據圖5，隨著反饋增益系數的增大，式（4）的混沌運動會經歷倍周期分岔最后被控制成為簡單的周期運動。類似地，并給定一個正的增益系數，系統動力學行為隨時滯量的演變（見圖6）。根據圖6，式（4）的混沌運動會隨時滯量的增加而最終演變為周期振動。這說明在正的反饋增益系數下，時滯速度反饋能有效地控制相對轉動系統的混沌運動。由于相對轉動角度ψ1＝θ1－θ2，根據式（5）中式（4）和式（1）的反饋增益系數的正比例關系可知，在正的反饋增益系數下，時滯速度反饋也能夠在一定程度上控制兩質量轉動系統式（1）的復雜運動。

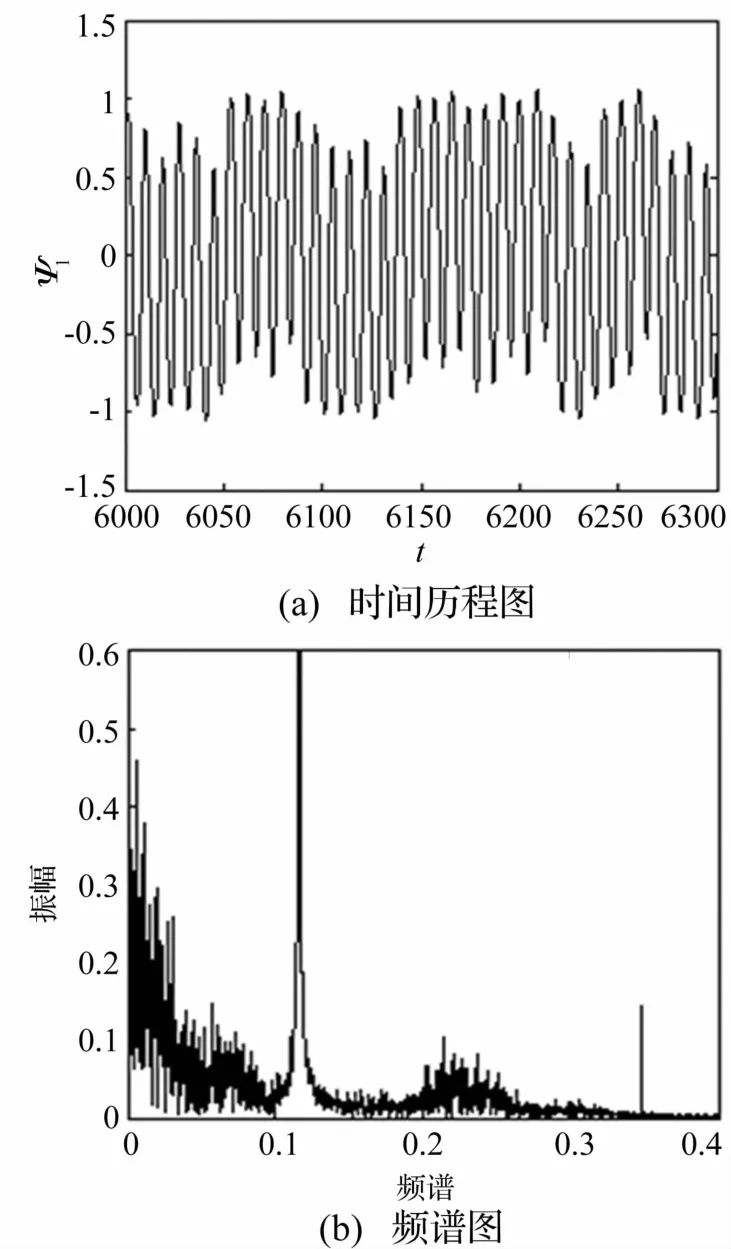
圖4 f＝0．412時系統（6）Fig．4（a）Diagram of time-history and（b）frequency spectrum of system（6）when f＝0．412

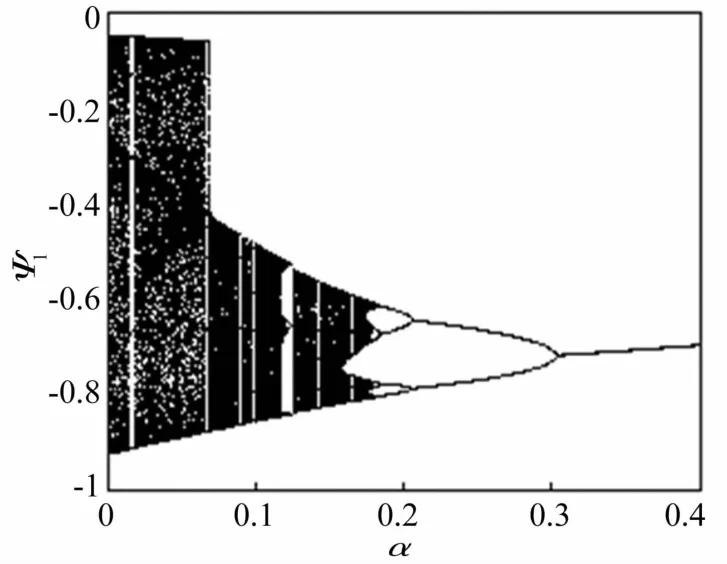
圖5 f＝0．412和τ＝0．2時受控系統（4）隨增益α分岔圖Fig．5 Bifurcation diagram of the gainαof the controlled system（4）when f＝0．412 andτ＝0．2

3.2 安全域侵蝕控制的數值仿真

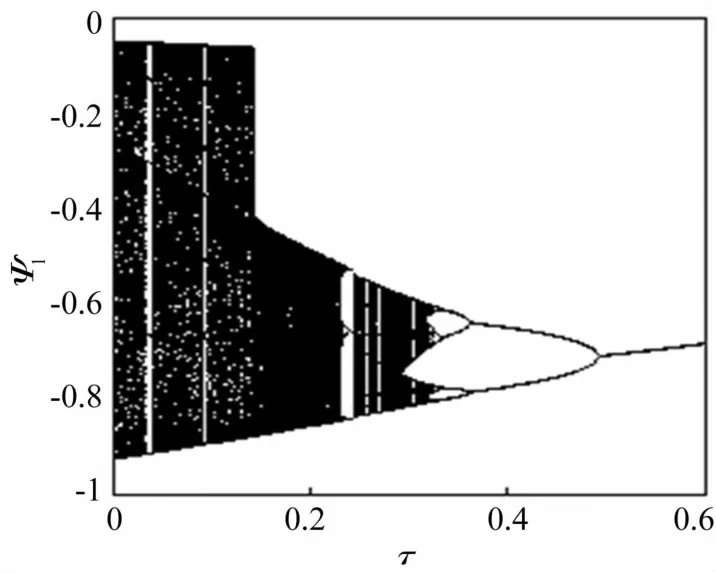
圖6 f＝0．412和α＝0．1時系統（4）隨時滯τ分岔圖Fig．6 Bifurcation diagram of the delayτof the controlled system（4）when f＝0．412 andα＝0．1

當外激勵f＝0．355＜f0＝0．377 7時，根據上節的理論分析，在正得的反饋增益系數下，無論時滯量取何值，系統（4）均不發生同宿分岔，因此安全域邊界不會分形，這一點由圖7（a），7（b）和7（c）證實。不僅如此，如圖7（a），7（b）和7（c）所示，隨著時滯量的增加，系統的安全域面積有所增大。而當外激勵 f＞f0＝0．377 7，根據理論預測，無時滯反饋控制的情況下，系統會發生同宿分岔從而引起安全域侵蝕，這與圖7（d）中安全域的分形邊界相吻合。隨著時滯量的增大，系統的安全域邊界分形程度明顯減弱：如τ＝1時，盡管系統的安全域邊界仍有分形，但安全域的面積有所增大（見圖7（e））。數值仿真得到的f＝0．412時安全域侵蝕的時滯臨界值與根據式（21）計算得到的的臨界值基本吻合（見圖2）。當時滯量τ增大到1．95時，系統的安全域邊界變得光滑，安全域侵蝕現象被完全抑制，見圖7（f）。綜上所述，在正的反饋增益系數下，時滯速度反饋可以有效地抑制相對轉動系統式（4）的安全域侵蝕現象，從而在一定程度上抑制兩質量轉動系統式（1）的過度振動，保證系統的振動安全性。

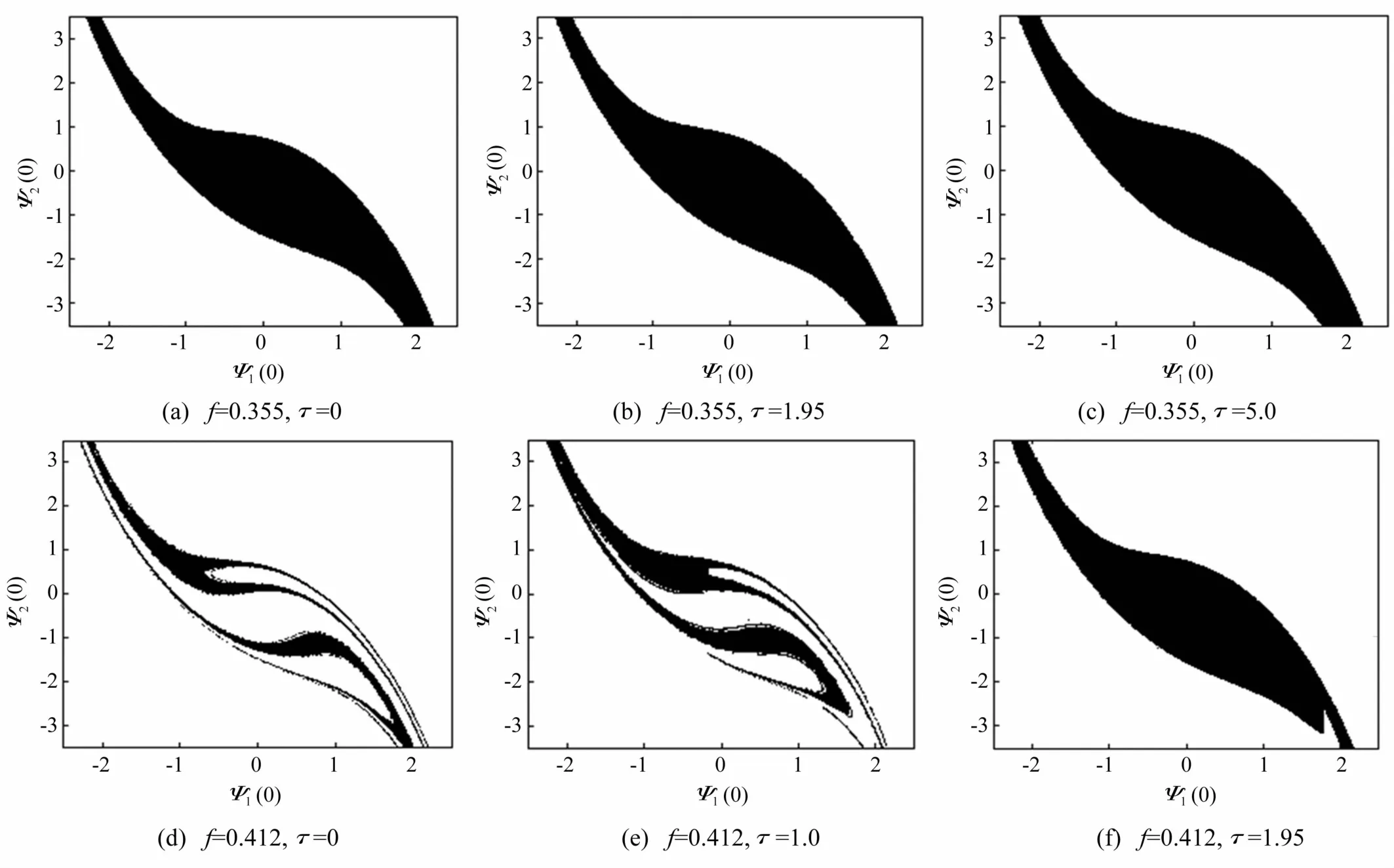
圖7 當α＝0．1時不同激勵振幅下受控系統（4）安全域隨時滯量的演變Fig．7 Evolution of safe basin of the controlled system（4）with the delay under different values of the excitation amplitude whenα＝0．1

4 結 論

以一類相對轉動系統為研究對象，對系統施加時滯速度反饋從而對系統的混沌運動和安全域侵蝕現象這兩類與初值敏感性相關的復雜動力學行為實施控制，利用Melnikov函數法分析了時滯速度反饋控制同宿分岔的機理，并運用數值算例來驗證理論分析的有效性。研究發現：在正的增益系數下，時滯速度反饋能夠有效地抑制系統的混沌運動和安全域侵蝕。

對非線性系統安全域的控制，時滯位移反饋中的時滯量常常存在雙向調節作用，即在較小的時滯量下，時滯位移反饋能夠有效地抑制系統的安全域侵蝕現象；但當時滯量大到一定程度，時滯位移反饋反而會引起安全域侵蝕。而在本文所考慮的時滯速度反饋相對轉動系統中，平衡點并不會隨著時滯量的變化而穩定性切換，這說明在正反饋增益系數下，系統的復雜動力學行為會隨著時滯量的增大變簡單；與時滯位移反饋不同，時滯速度反饋對系統的混沌運動和安全域侵蝕能夠起到單向的抑制作用。因此，時滯速度反饋用于抑制相對轉動系統的復雜動力學行為是一種穩定的控制策略。

［1］趙武，劉彬，石培明，等．一類非線性相對轉動周期系統的平衡穩定性分析［J］．物理學報，2006，55（8）：3852－3857．

ZHAO Wu，LIU Bin，SHI Pei-ming，et al．Anslysis of stability of the equilibrium state of periodic motion in a nonlinear relative rotation system［J］．Acta Physica Sinica，2006，55（8）：3852－3857．

［2］劉爽，劉彬，張業寬，等．一類時滯非線性相對轉動系統的Hopf分岔與周期解的穩定性［J］．物理學報，2010，59（1）：38－43．

LIU Shuang，LIU Bin，ZHANG Ye-kuan，et al．Hopf bifurcation and stability of periodic solutions in a nonlinear relative rotation dynamical system with time delay［J］．Acta Physica Sinica，2010，59（1）：38－43．

［3］劉浩然，朱占龍，石培明．一類相對轉動的時滯非線性動力系統的穩定性分析［J］．物理學報，2010，59（10）：6770－6771．

LIU Hao-ran，ZHU Zhan-long，SHI Pei-ming．Stability analysis of a relative rotation time-delay nonlinear dynamic system［J］．Acta Physica Sinica，2010，59（10）：6770－6771．

［4］張文明，李雪，劉爽，等．一類非線性相對轉動系統的混沌運動及多時滯反饋控制［J］．物理學報，2013，62（9）：095402．

ZHANGWen-ming，LIXue，LIU Shuang，et al．Chaos and the control of multi-time delay feedback for some nonlinear relative rotation system［J］．Acta Physica Sinica，2013，62（9）：095402．

［5］喬杰敏，王坤，李秀菊，等．兩類相對轉動非線性動力學系統的統一動力學模型及混沌運動［J］．燕山大學報，2009，33（2）：159－162．

QIAO Jie-min，WANG Kun，LI Xiu-ju，et al．Unified dynamics model of two kind of relative rotation nonlinear dynamics system and chaos［J］．Journal of Yanshan University，2009，33（2）：159－162．

［6］候東曉，趙紅旭，劉彬．一類含Mathieu-Duffing振子的相對轉動系統的分岔和混沌［J］．物理學報，2013，62（23）：234501．

HOU Dong-xiao，ZHAO Hong-xu，LIU Bin．Bifurcation and chaos in some relative rotation systems with Mathieu-Duffing oscillator［J］．Acta Physica Sinica，2013，62（23）：234501．

［7］Luo SK．The theory of relativistic analyticalmechanics of the rotational systems［J］．Applied Mathematics and Mechanics，1998，19（1）：45－57．

［8］Thompson JMT，Rainey FC T，Soliman MS．Ship stability criteria based on chaotic transients from incursive fractals［J］．Philosophical Transactions of the Royal Society，1995，332（1）：149－167．

［9］Gan C B．Noise-Induced chaos and basin erosion in softening Duffing oscillator［J］．Chaos，Solitons and Fractals，2005，25（5）：1069－1081．

［10］Rega G，Valeria S．Bifurcation，response scenarios and dynamic integrity in a single-modemodel of noncontactatomic forcemicroscopy［J］．Nonlinear Dynamics，2013，73（1／2）：101－123．

［11］Xu J，Yu P．Delay-induced bifurcations in a nonautonomous system with delayed velocity feedbacks［J］．International Journal of Bifurcation and Chaos，2004，14（8）：2777－2798．

［12］Shao S，Masti K M，Younis MI．The effect of time-delayed feedback controller on an electrically actuatedresonator［J］．Nonlinear Dynamics，2013，74（1／2）：257－270．

［13］Alsaleem F M，Younis MI．Stabilization of electrostatic MEMS resonators using a delayed feedbackcontroller［J］．Smart Materials and Structures，2010，19（3）：035016．

［14］尚慧琳，文永蓬．軟彈簧Duffing系統的安全域侵蝕及其時滯速度反饋控制［J］．振動與沖擊，2012，31（8）：11－15．

SHANG Hui-lin，WEN Yong-peng Erosion of safe basins in a softening duffing system and its control with time-delay position feedback［J］．Journal of Vibration and Shock，2012，31（8）：11－15．

［15］Shang H L．Control of fractal erosion of safe basins in a Holmes-Duffing system via delayed position feedbacks［J］．Chinese Physics Letters，2011，28（1）：010502．

［16］Shang H L，Xu J．Delayed feedbacks to control the fractal erosion of safe basins in a parametrically excited system［J］．Chaos，Solitons and Fractals，2009，41（4）：1880－1896．

［17］Thomsen J J，Fidlin A．Analytical approximations for stickslip vibration amplitudes［J］．International Journal of Nonlinear Mechanics，2003，38（3）：389－403．

Com p lex dynam ic behaviors of relative rotation system and its control by delayed velocity feedback

SHANGHui-lin1，LIWei-yang1，HAN Yuan-bo1，WEN Yong-pen2
（1．School of Mechanical Engineering，Shanghai Institute of Technology，Shanghai200235，China；2．College of Urban Railway Transportation，Shanghai University of Engineering Science，Shanghai201620，China）

The complex dynamic behaviors a typical relative rotation system，such as chaos and erosion of safe basin，induced by the variation of system parameterswere investigated．In order to keep the reliability of the oscillation of the system，delayed velocity feedback was applied in the system to suppress these complex dynamic behaviors．The critical excitation for chaos and erosion of safe basin of the delayed velocity feedback controlled system was obtained by the Melnikov method．Then complex dynamic behaviors of the systems with different system parameters were stimulated numerically，which verifies the validity of the theoretical prediction．It is found that the delayed velocity feedback could be used as an effectivemethod on suppressing chaos and erosion of safe basin of relative rotation systems．

relative rotation system；Melnikovmethod；delayed velocity feedback；chaos；safe basin

TP242；O322

A

10．13465／j．cnki．jvs．2015．12．022

國家自然科學基金項目（11472176）；上海市自然科學基金項目（15ZR1419200）；上海市教委晨光計劃項目（11CG61）

2014－01－02 修改稿收到日期：2014－04－24

尚慧琳 女，博士，副教授，1983年生