矩形孔徑參量陣相控非線性聲場(chǎng)建模與實(shí)驗(yàn)研究

朱建軍，李海森，魏玉闊，陳寶偉，周 天

（1．哈爾濱工程大學(xué)水聲技術(shù)重點(diǎn)實(shí)驗(yàn)室，哈爾濱 150001；2．哈爾濱工程大學(xué)水聲工程學(xué)院，哈爾濱 150001）

矩形孔徑參量陣相控非線性聲場(chǎng)建模與實(shí)驗(yàn)研究

朱建軍1，2，李海森1，2，魏玉闊1，2，陳寶偉1，2，周 天1，2

（1．哈爾濱工程大學(xué)水聲技術(shù)重點(diǎn)實(shí)驗(yàn)室，哈爾濱 150001；2．哈爾濱工程大學(xué)水聲工程學(xué)院，哈爾濱 150001）

為了解決一階拋物近似KZK方程無(wú)法直接對(duì)相控非線性聲場(chǎng)進(jìn)行建模的問(wèn)題，依據(jù)原頻聲場(chǎng)準(zhǔn)直特性構(gòu)建等效參量陣原頻自然指向性聲場(chǎng)模型，建立其與原頻相控聲場(chǎng)的等效關(guān)系，將相控非線性聲場(chǎng)的建模問(wèn)題轉(zhuǎn)換為等效參量陣聲源條件的求解問(wèn)題，同時(shí)提出算子分裂時(shí)域有限差分?jǐn)?shù)值計(jì)算方法，實(shí)現(xiàn)了基于KZK拋物方程的矩形孔徑參量陣相控非線性聲場(chǎng)數(shù)值計(jì)算。以SES2000標(biāo)準(zhǔn)型參量聲吶輻射相控非線性聲場(chǎng)為研究對(duì)象，開(kāi)展了計(jì)算機(jī)仿真和水池對(duì)比實(shí)驗(yàn)研究，研究結(jié)果驗(yàn)證了構(gòu)建聲場(chǎng)模型及其數(shù)值計(jì)算方法的有效性。

矩形孔徑參量陣；相控非線性聲場(chǎng)；聲場(chǎng)建模

近年來(lái)，隨著非線性聲學(xué)理論的不斷發(fā)展，聲波的非線性效應(yīng)被逐步應(yīng)用于水聲工程、生物醫(yī)學(xué)和空氣聲學(xué)等領(lǐng)域［1－3］。當(dāng)參量陣同時(shí)輻射兩種頻率的高強(qiáng)度有限振幅波時(shí)，聲場(chǎng)中會(huì)產(chǎn)生聲散射聲—差頻波、和頻波與諧頻波［4］。這一非線性效應(yīng)有效解決了傳統(tǒng)小孔徑基陣無(wú)法相控發(fā)射低頻、寬帶、無(wú)旁瓣窄波束的問(wèn)題［5］，使聲學(xué)換能器突破了瑞利限的限制。基于這一技術(shù)特點(diǎn)，水聲中參量聲吶的差頻探測(cè)技術(shù)在淺地層剖面探測(cè)［6］、淺海遠(yuǎn)程通信［7］、海底掩埋物探測(cè)［8］等領(lǐng)域獲得了傳統(tǒng)線性聲吶無(wú)法比擬的優(yōu)越性能。

參量聲吶科學(xué)設(shè)計(jì)與合理應(yīng)用均需以非線性聲場(chǎng)（參量聲場(chǎng)）研究為前提，涉及聲場(chǎng)建模、計(jì)算以及相關(guān)實(shí)驗(yàn)驗(yàn)證研究。除Westervelt方程［9］、Burgers方程［10］等經(jīng)典方程，KZK（Khokhlov Zabolotskaya Kuznetsov）方程［11］是目前為止最為精準(zhǔn)的參量聲場(chǎng)建模方程［12］。這是由于實(shí)際參量陣的孔徑均具有一定的形狀和大小，必須考慮聲波衍射效應(yīng)；所有介質(zhì)均具有熱傳導(dǎo)性和黏滯性，介質(zhì)對(duì)聲波的吸收效應(yīng)也不可忽略，上述三種建模方程中僅KZK方程全面考慮了聲波的衍射效應(yīng)、聲吸收效應(yīng)以及非線性效應(yīng)。KZK方程在用于參量聲場(chǎng)研究時(shí)既具有其自身特點(diǎn)，也存在一些尚未有效解決的問(wèn)題：① 由于圓形孔徑參量陣具有軸對(duì)稱的聲場(chǎng)分布特征，易于建模［13］，從研究之初就多針對(duì)這一聲場(chǎng)結(jié)構(gòu)開(kāi)展研究，而矩形孔徑參量陣輻射聲場(chǎng)研究相對(duì)薄弱；② 以應(yīng)用需求為導(dǎo)向，針對(duì)生物醫(yī)學(xué)非線性諧波場(chǎng)的研究較為深入［14］，針對(duì)水聲中廣泛應(yīng)用的差頻聲場(chǎng)研究相對(duì)較少；③ 受KZK方程一階拋物近似僅能描述主軸附近±15°范圍內(nèi)參量聲場(chǎng)的限制，無(wú)法采用KZK方程直接對(duì)相控參量聲場(chǎng)進(jìn)行描述［15］。

針對(duì)近年來(lái)水聲領(lǐng)域?qū)匦慰讖较嗫貐⒘筷嚥铑l探測(cè)技術(shù)的迫切需求以及相控參量聲場(chǎng)研究中存在的上述問(wèn)題，從矩形孔徑參量聲場(chǎng)建模與數(shù)值計(jì)算、相控參量聲場(chǎng)建模以及實(shí)驗(yàn)驗(yàn)證等幾個(gè)方面開(kāi)展重點(diǎn)研究，在對(duì)矩形孔徑參量陣自然指向性參量聲場(chǎng)建模的前提下，針對(duì)一級(jí)拋物近似KZK方程無(wú)法直接對(duì)相控參量聲場(chǎng)進(jìn)行建模的問(wèn)題建立等效參量陣坐標(biāo)系，通過(guò)基陣坐標(biāo)變換將相控參量聲場(chǎng)的建模問(wèn)題轉(zhuǎn)變?yōu)榈刃⒘筷嚶曉礂l件的求解問(wèn)題，并在等效參量陣坐標(biāo)系下實(shí)現(xiàn)相控參量聲場(chǎng)的數(shù)值計(jì)算。

1 自然指向性參量聲場(chǎng)建模與數(shù)值計(jì)算

1.1 非擴(kuò)散參量聲場(chǎng)KZK建模方程

由非線性聲學(xué)基本方程推得近似至二階微小項(xiàng)的非線性波動(dòng)方程為［16］：

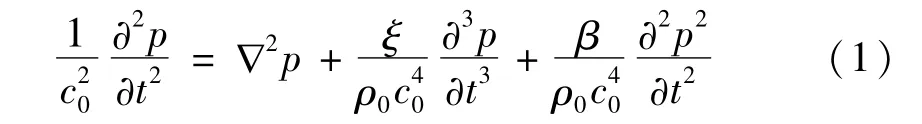
式中：p為聲壓，c0為小信號(hào)聲速，ρ0為介質(zhì)密度，ξ為吸收系數(shù)；β為非線性系數(shù)。由Muir平方根展開(kāi)關(guān)系［17］，取一級(jí)拋物近似并做t′＝t－z／c0的參數(shù)變換，得到笛卡爾坐標(biāo)系下的KZK方程為：

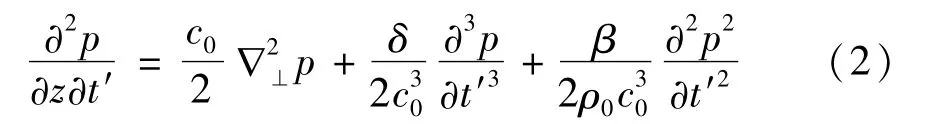
式中：δ為介質(zhì)熱粘吸收損耗因數(shù)，?2⊥為笛卡爾坐標(biāo)系下的拉普拉斯算子。公式中右側(cè)三項(xiàng)因式依次表示聲衍射、聲吸收和非線性效應(yīng)。為便于在笛卡爾坐標(biāo)系中描述參量聲場(chǎng)，定義矩形孔徑參量陣坐標(biāo)系見(jiàn)圖1，其中基陣長(zhǎng)、寬分別為2a和2b（a≥b），以輻射面中心點(diǎn)為坐標(biāo)原點(diǎn)，基陣輻射面與xy平面重合，z為基陣法線方向，同時(shí)定義孔徑縱橫比R＝b／a≤1。

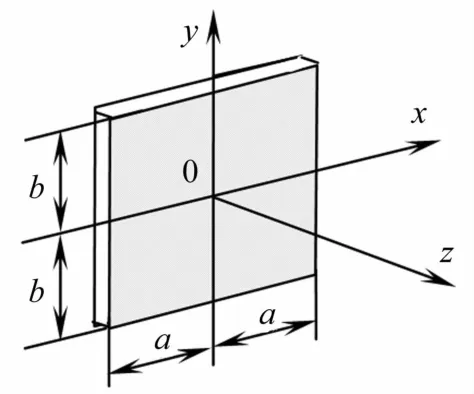
圖1 矩形孔徑參量陣坐標(biāo)系Fig．1 Rectangularaperture parametric array coordinate

由于超出菲涅爾區(qū)后聲波將以球面擴(kuò)展方式傳播，聲場(chǎng)區(qū)域也隨之?dāng)U大，從而聲場(chǎng)計(jì)算量也會(huì)隨之增加，聲場(chǎng)建模需充分考慮這一問(wèn)題，以獲得優(yōu)化的聲場(chǎng)建模方案。Aanonsen等［18］提出參數(shù)去量綱化法實(shí)現(xiàn)擴(kuò)散聲場(chǎng)至非擴(kuò)散聲場(chǎng)的變換，達(dá)到了降低聲場(chǎng)計(jì)算量的目的，KZK方程中參量的去量綱化形式為：σ＝z／R0，ux＝x／［a（1+σ）］，uy＝y(tǒng)／［a（1+σ］，P＝p（1+ σ）／p0，τ＝ω0t′－k0（x2+y2）／［2R0（1+σ）］，其中R0為瑞利距離，k0為原頻波數(shù)，t′＝t－z／c0，p（x，y，z，t）為（x，y，z）場(chǎng)點(diǎn)處聲壓，p0為輻射面特征聲壓。將去量綱化參量代入式（2）并對(duì)等式兩側(cè)做時(shí)間積分，推得非擴(kuò)散聲場(chǎng)中的KZK拋物方程又稱TBE（Transformed Beam E-quation）方程［19］：

式中：A＝α0R0為聲吸收系數(shù)，α0為衰減系數(shù)，N＝R0／zs為非線性參數(shù)，zs為沖擊距離。就基于式（3）在非擴(kuò)散聲場(chǎng)中對(duì)參量聲場(chǎng)進(jìn)行數(shù)值計(jì)算。

1.2 參量陣聲源條件

參量陣輻射面上輻射聲波的聲壓值為：

p（x，y，z＝0，t）＝p0·e（t）·s（t）·H（x，y）（4）式中：p0為初始聲壓幅值，e（t）為信號(hào)包絡(luò)，s（t）為載頻信號(hào)，H（x，y）為聲源分布函數(shù)，其去量綱化表示形式為：

1.3 聲場(chǎng)數(shù)值計(jì)算

由于KZK方程是高階拋物方程，難以求出一般形式的封閉解析解，因此只能采用數(shù)值計(jì)算方法對(duì)聲場(chǎng)進(jìn)行計(jì)算。目前，KZK方程數(shù)值求解方法主要包括時(shí)域法和頻域法［20］，頻域法將聲場(chǎng)表示為傅里葉級(jí)數(shù)展開(kāi)各次諧波疊加的形式，但實(shí)際選取諧波階次有限（最大諧波階次稱截?cái)嘀C波次數(shù)），有限的截?cái)嘀C波次數(shù)阻斷了原頻波向高次諧波以及高次諧波向低次諧波的能量傳遞，且在截?cái)嘀C波頻率處形成能量堆積，計(jì)算誤差逐步增大。在計(jì)算短脈沖或?qū)拵盘?hào)激勵(lì)參量聲場(chǎng)時(shí)，頻域法必須保留大量頻譜成分，而其計(jì)算量與截?cái)嘀C波次數(shù)的平方成比例，從而計(jì)算量將很大，并且頻域法難以對(duì)相控聲場(chǎng)等具有非一致聲源條件的聲場(chǎng)進(jìn)行建模。時(shí)域法不僅可以使用非一致性聲源條件，而且基于波形的研究更加直觀，因此采用時(shí)域法對(duì)參量聲場(chǎng)進(jìn)行數(shù)值計(jì)算。

定義τ時(shí)刻非擴(kuò)散參量聲場(chǎng)中場(chǎng)點(diǎn)（ux，uy，σ）處聲壓的離散表達(dá)形式為：

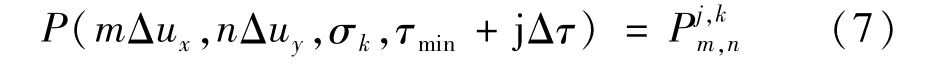
式中，Δux、Δuy分別為x，y向變化步長(zhǎng)，Δτ時(shí)間變化步長(zhǎng)，波束主軸方向傳播距離σk＝∑Δσl，l∈（0，k－1），Δσl＝（1+σk）2Δσ0，σ0為初始步長(zhǎng)。從而，數(shù)值積分約束區(qū)間為j∈［jmin，jmax］、m∈［mmin，mmax］和n∈［nmin，nmax］。同時(shí)定義聲場(chǎng)的空間和時(shí)間零聲壓邊界條件分別為：

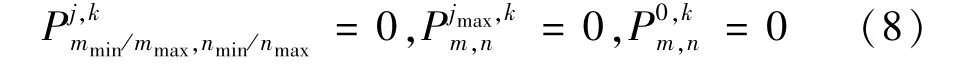
由于矩形孔徑參量陣自然指向性聲場(chǎng)在x軸和y軸方向上均對(duì)稱，因此計(jì)算1／4輻射聲場(chǎng)區(qū)域即可對(duì)整個(gè)聲場(chǎng)空間進(jìn)行描述，此時(shí)引入附加邊界條件：

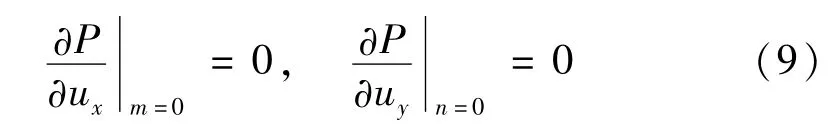
取m∈［0，mmax］和n∈［0，nmax］。但即便如此，矩形孔徑參量陣的聲場(chǎng)計(jì)算仍是針對(duì)三維空間的數(shù)值計(jì)算，而圓形孔徑參量陣的聲場(chǎng)計(jì)算區(qū)域是基陣半徑和聲軸所在的二維平面，這正是矩形孔徑參量陣聲場(chǎng)研究的復(fù)雜性和難點(diǎn)所在。借鑒Lee［21］采用的算子分裂法求解思想，提出矩形孔徑自然指向性參量聲場(chǎng)時(shí)域有限差分?jǐn)?shù)值計(jì)算方法，算法結(jié)構(gòu)見(jiàn)圖2。

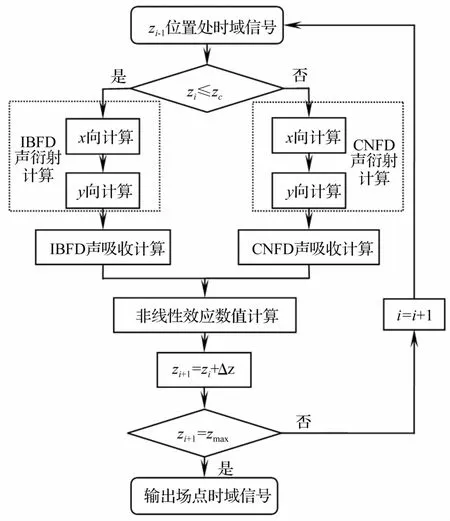
圖2 時(shí)域有限差分?jǐn)?shù)值計(jì)算方法Fig．2 Time domain finite difference numerical calculation method

在聲源附近（z≤zc，zc＝0．1R0），采用距離上一階精度近似的隱式后向有限差分（Implicit Backward Finite Difference，IBFD）格式，以較小的距離變化步長(zhǎng)消除聲源條件中階躍函數(shù)不連續(xù)引起的近場(chǎng)數(shù)值振蕩，提高近場(chǎng)計(jì)算精度；在此區(qū)域外，采用絕對(duì)穩(wěn)定的二階精度近似Crank-Nicolson有限差分（Crank-Nicolson Finite Difference，CNFD）格式，在保證算法穩(wěn)定性的同時(shí)可逐漸增大步長(zhǎng)進(jìn)一步減小聲場(chǎng)計(jì)算量。

2 相控參量聲場(chǎng)建模

2.1 等效參量陣坐標(biāo)系

一級(jí)拋物近似KZK方程僅能有效描述聲軸±15°范圍內(nèi)的參量聲場(chǎng)，對(duì)具有超高指向性（通常＜5°）的參量陣來(lái)說(shuō)，足以滿足其自然指向性聲場(chǎng)的建模要求，但在描述較大相控角度的聲場(chǎng)時(shí)將失效［22］。

由參量陣基本理論可知，參量陣輻射面附近＜（L1＝4b2／λ0）的區(qū)域內(nèi)原頻波具有準(zhǔn)直特性，該區(qū)域內(nèi)垂直聲軸的聲場(chǎng)截面與基陣輻射面的大小和形狀完全相同，而該區(qū)域至菲涅爾區(qū)外沿的聲場(chǎng)中原頻波做柱形擴(kuò)展傳播［23］，傳播距離L2＝4（a2－b2）／λ0，矩形孔徑參量陣原頻聲場(chǎng)分布見(jiàn)圖3。

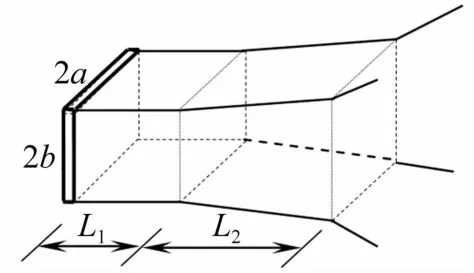
圖3 矩形孔徑參量陣原頻聲場(chǎng)分布Fig．3 Rectangular parametric array primary field distribution

對(duì)于相控聲場(chǎng)，波束主極大偏離了基陣法線方向，此時(shí)，提出等效參量陣的概念，相控參量聲場(chǎng)被認(rèn)為由該等效參量陣產(chǎn)生，且此等效參量陣原頻聲場(chǎng)仍滿足準(zhǔn)直特性。建立等效參量陣二維坐標(biāo)系xp－zp，使zp軸與等效參量陣法線重合（見(jiàn)圖4），從而相控參量聲場(chǎng)也可由該坐標(biāo)系進(jìn)行描述。

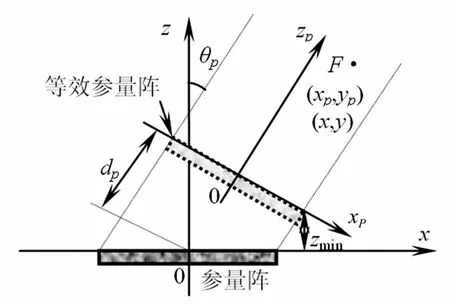
圖4 等效參量陣坐標(biāo)系Fig．4 Equivalent parametric array coordinate

由圖4的幾何結(jié)構(gòu)推導(dǎo)出同一場(chǎng)點(diǎn)F在x－z和xp－zp兩坐標(biāo)系中坐標(biāo)（x，z）和（xp，zp）間的變換關(guān)系為：

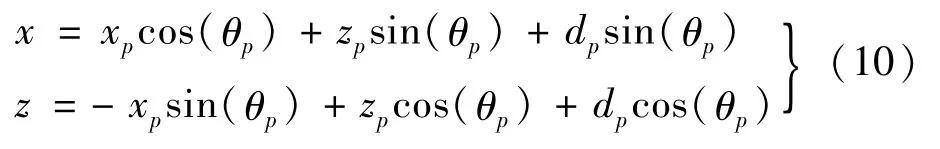
2.2 等效參量陣聲源條件求解

由等效參量陣原頻準(zhǔn)直特性可知，xp－zp坐標(biāo)系符合KZK方程聲場(chǎng)建模的條件，只要根據(jù)x－z和xp－zp兩坐標(biāo)系間的坐標(biāo)變換關(guān)系求解等效參量陣聲源條件，即可在xp－zp坐標(biāo)系中采用非擴(kuò)散參量聲場(chǎng)計(jì)算方法實(shí)現(xiàn)相控參量聲場(chǎng)數(shù)值計(jì)算，將相控聲場(chǎng)建模問(wèn)題轉(zhuǎn)換為等效參量陣聲源條件的求解問(wèn)題。由于聲源附近非線性作用剛剛開(kāi)始，聲場(chǎng)中最主要的頻率成分仍為原頻，聲散射聲信號(hào)能量特別微弱，可忽略不計(jì)。此時(shí)聲源附近原頻聲場(chǎng)可近似為線性聲場(chǎng)，從而等效參量陣的聲源條件可近似由線性聲場(chǎng)計(jì)算方法求解得到。

假設(shè)參量陣輻射面周圍為剛性障板，基于矩形增量區(qū)域劃分模型計(jì)算原頻聲場(chǎng)，聲場(chǎng)建模原理見(jiàn)圖5，聲場(chǎng)的離散形式表示為［24］：

其中，N為劃分面元個(gè)數(shù)，Δs為面元面積，r為場(chǎng)點(diǎn)至面元的距離，un為第n個(gè)面元的表面復(fù)速度。對(duì)于一致激勵(lì)聲源，各面元表面復(fù)速度相同，而對(duì)于非一致激勵(lì)的情況（如相控基陣），不同面元具有不同的un。

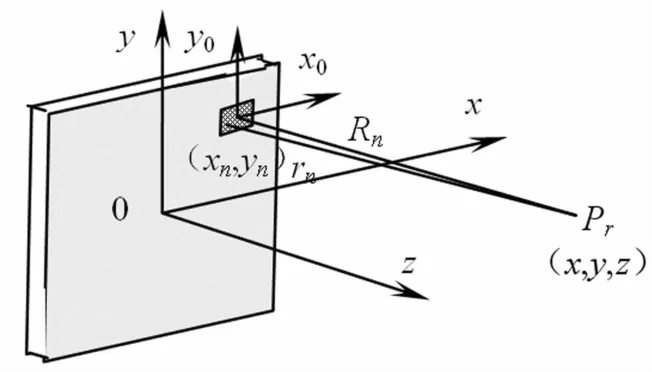
圖5 原頻聲場(chǎng)計(jì)算模型Fig．5 Primary sound field calculation model

同時(shí)，推得相控角度為θp時(shí)等效參量陣輻射面上各場(chǎng)點(diǎn)在x－z坐標(biāo)系中的坐標(biāo)為：

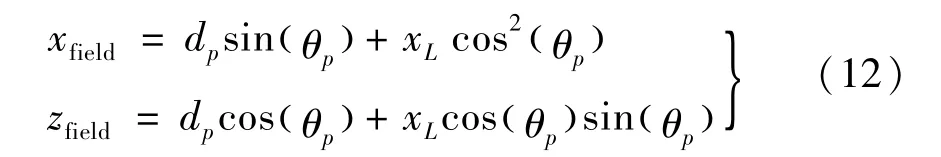
式中：xL∈［－a，a］為橫坐標(biāo)，yw∈［－b，b］為縱坐標(biāo)，yfield＝y(tǒng)w。因此，式（12）可用于等效參量陣聲源條件求解。

相控角度為0°和15°時(shí)110 kHz原頻波束上垂直聲軸的聲場(chǎng)剖面如圖6所示，參量陣孔徑為0．22 m× 0．22 m，dp＝6．7 cm（L1＝3．55 m）。0°相控聲場(chǎng)剖面在x，y兩維方向上均對(duì)稱，而15°相控聲場(chǎng)主軸在x軸向發(fā)生了相應(yīng)偏移，但在y軸向仍對(duì)稱。因此，相控參量聲場(chǎng)數(shù)值計(jì)算時(shí)xp、yp兩維方向上積分區(qū)間可定義為m∈［m′min，m′max］和n∈［0，nmax］，m′min、m′max對(duì)應(yīng)等效參量陣xp軸向孔徑，即相控參量聲場(chǎng)可用yp軸方向上對(duì)稱聲場(chǎng)的1／2自然指向性聲場(chǎng)來(lái)描述。

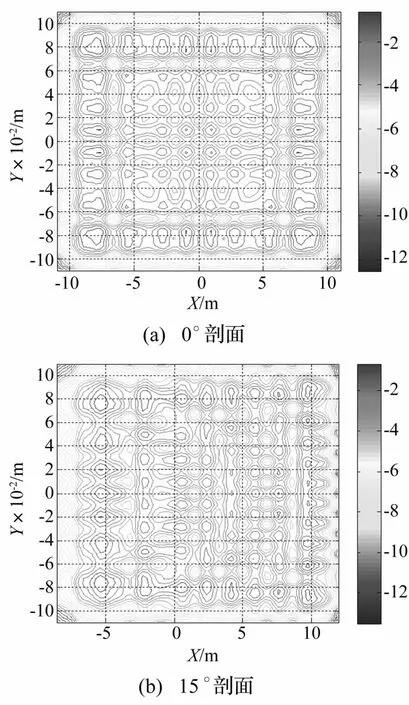
圖6 原頻準(zhǔn)直區(qū)域內(nèi)聲場(chǎng)剖面Fig．6 Acoustic field profiles in thecollimate zone

3 水池實(shí)驗(yàn)驗(yàn)證分析

3.1 實(shí)驗(yàn)方案

水池實(shí)驗(yàn)在水聲技術(shù)重點(diǎn)實(shí)驗(yàn)室的信道水池進(jìn)行，水池大小為45 m×6 m×5 m，四面?zhèn)缺诰佋O(shè)消聲尖劈，吸聲截止頻率50～1 MHz，僅在19．2 kHz時(shí)存在一定的背景噪聲干擾，但低于7 dB。基本實(shí)驗(yàn)系統(tǒng)由德國(guó)Innomar公司SES2000標(biāo)準(zhǔn)型參量聲吶（原頻中心頻率100 kHz，差頻4 kHz、5 kHz、6 kHz、8 kHz、10 kHz、12 kHz、15 kHz）、Reson TC4038標(biāo)準(zhǔn)水聽(tīng)器（帶寬10～800 kHz，靈敏度－227dBre 1V／μPa）、TOPVIEW2000多通道采集器（最高采樣頻率25 MHz）和HY 1200聲速剖面儀構(gòu)成（用于水池中聲速剖面測(cè)量，為聲場(chǎng)建模提供準(zhǔn)確的聲速信息）。參量陣布放水深1．5 m，經(jīng)剛性轉(zhuǎn)接架裝于可旋轉(zhuǎn)的吊裝桿上，水聽(tīng)器布放于小行車上，并處于同一深度。通過(guò)聲軸上參量信號(hào)波形測(cè)試、原頻和差頻相控指向性聲場(chǎng)測(cè)試以及軸向聲場(chǎng)測(cè)試，與相同參數(shù)的計(jì)算機(jī)仿真結(jié)果進(jìn)行比對(duì)，對(duì)本研究矩形孔徑參量陣相控參量聲場(chǎng)建模與數(shù)值計(jì)算方法的有效性進(jìn)行驗(yàn)證，實(shí)驗(yàn)方案（見(jiàn)圖7）。

3.2 實(shí)驗(yàn)結(jié)果及分析

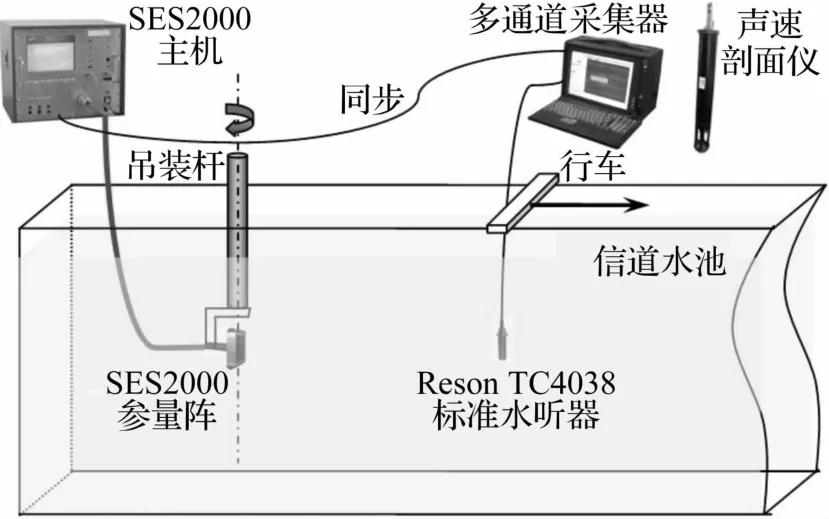
圖7 實(shí)驗(yàn)方案設(shè)計(jì)圖Fig．7 Diagram of the experimental scheme

SES2000參量陣孔徑為0．22 m×0．22 m，實(shí)測(cè)1．5 m處水中聲速為1 474m／s。相控參量聲場(chǎng)建模和數(shù)值計(jì)算在ThinkStation 4158－FB9工作站上進(jìn)行，聲場(chǎng)建模參量為：a＝0．11 m，b＝0．11 m，β＝3．6，原頻聲源級(jí)239 dB，Δx＝Δy＝0．03，ux＝uy＝10，IBFD計(jì)算時(shí)σ＝0．001（1+σ）2，CNFD計(jì)算時(shí)σ＝0．003（1+σ）2，fs＝3．075 MHz。水池實(shí)驗(yàn)測(cè)量數(shù)據(jù)處理時(shí)對(duì)標(biāo)準(zhǔn)水聽(tīng)器不同頻率的靈敏度進(jìn)行了一致性補(bǔ)償處理。

12 m處仿真與實(shí)測(cè)參量信號(hào)波形及頻譜如圖8所示，差頻信號(hào)頻率為12 kHz。實(shí)測(cè)兩原頻信號(hào)的頻譜幅度略微不同且信號(hào)波形出現(xiàn)了一定的振鈴效應(yīng)，分析原因主要是由于實(shí)際聲吶系統(tǒng)響應(yīng)難以做到完全一致且實(shí)測(cè)信號(hào)中混入了噪聲干擾（電噪聲和環(huán)境噪聲等），而系統(tǒng)帶寬有限是引起振鈴效應(yīng)的主要因素。但對(duì)比可以看出，總體上仿真與實(shí)測(cè)結(jié)果吻合得較好，初步驗(yàn)證了聲場(chǎng)建模與數(shù)值計(jì)算方法的有效性。

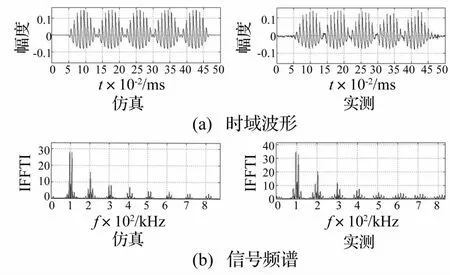
圖8 參量信號(hào)波形及頻譜Fig．8Waveform and spectrum of parametric signal

同時(shí)，仿真了7 m和12 m處0°∶5°∶30°七個(gè)相控角度的差頻指向性，并與實(shí)測(cè)結(jié)果進(jìn)行對(duì)比（見(jiàn)圖9）。由于SES2000最大相控角度為16°，因此僅測(cè)試了0°∶5°∶15°四個(gè)相控角度的指向性。圖中差頻主波束以外角度上噪聲水平高于理論仿真結(jié)果，這是由于在水池環(huán)境噪聲及實(shí)驗(yàn)系統(tǒng)電噪聲等干擾因素影響下，隨著測(cè)量角度增大信噪比逐漸降低造成的，在±10°范圍外信噪比低于實(shí)驗(yàn)系統(tǒng)的檢測(cè)閾，從而表現(xiàn)為主瓣外實(shí)測(cè)值（噪聲）高于仿真指向性。

最后，對(duì)95 kHz原頻信號(hào)以及12 kHz和15 kHz差頻信號(hào)軸向聲場(chǎng)的仿真與實(shí)測(cè)結(jié)果進(jìn)行了比對(duì)（見(jiàn)圖10），兩者吻合較好，測(cè)量結(jié)果中差頻曲線出現(xiàn)了微小的起伏，分析其原因是由于差頻信號(hào)較弱，受環(huán)境噪聲、電噪聲以及小行車行走過(guò)程中引起的振動(dòng)等瞬態(tài)干擾造成的。

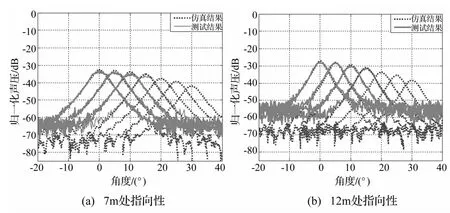
圖9 差頻指向性圖Fig．9 Directivity of differency frequency

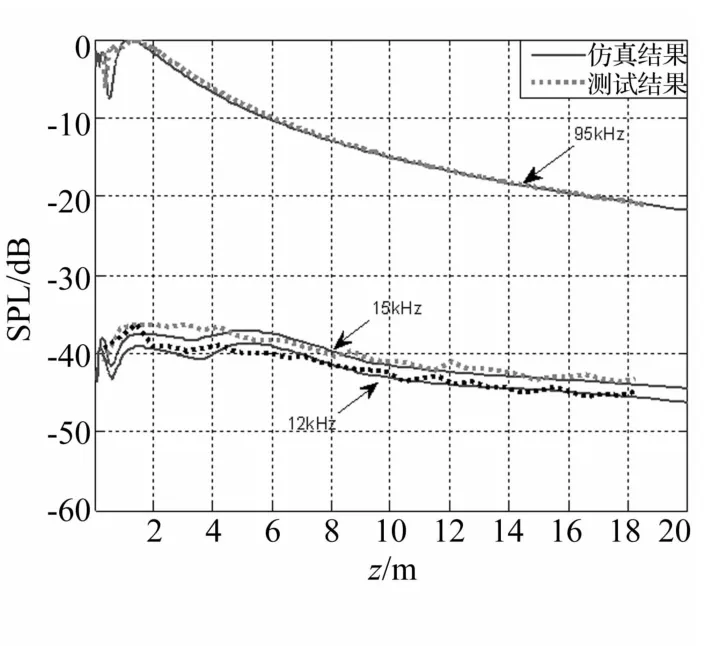
圖10 軸向聲場(chǎng)Fig．10 Axialacoustic field

由對(duì)比實(shí)驗(yàn)可知，參量聲場(chǎng)的仿真與實(shí)測(cè)結(jié)果整體上基本一致，充分驗(yàn)證了本文提出矩形孔徑相控參量聲場(chǎng)建模與數(shù)值計(jì)算方法的正確性和有效性。

4 結(jié) 論

系統(tǒng)地研究了矩形孔徑參量陣相控參量聲場(chǎng)的建模與數(shù)值計(jì)算方法，推導(dǎo)了矩形孔徑參量聲場(chǎng)的KZK建模方程，采用時(shí)域有限差分法實(shí)現(xiàn)了聲場(chǎng)的數(shù)值計(jì)算，解決了基于KZK方程的相控參量聲場(chǎng)的建模問(wèn)題。參量陣原頻聲場(chǎng)的準(zhǔn)直特性支持了參量陣相控參量聲場(chǎng)等效于其等效參量陣自然指向性聲場(chǎng)的結(jié)論，為利用一階近似KZK拋物方程進(jìn)行相控參量聲場(chǎng)建模提供了理論依據(jù)。同時(shí)，聲源條件求解問(wèn)題是相控參量聲場(chǎng)建模與數(shù)值計(jì)算的關(guān)鍵問(wèn)題，相控參量陣非一致性聲源條件的特點(diǎn)決定了時(shí)域有限差分法更適合于相控參量聲場(chǎng)數(shù)值計(jì)算。計(jì)算機(jī)仿真結(jié)果與SES2000標(biāo)準(zhǔn)型參量聲吶輻射相控參量聲場(chǎng)吻合得很好，驗(yàn)證了聲場(chǎng)建模和數(shù)值計(jì)算的正確性和有效性，研究成果可為相控參量聲吶設(shè)計(jì)及差頻海底探測(cè)研究提供理論依據(jù)和技術(shù)支持，對(duì)生物醫(yī)學(xué)和空氣聲學(xué)等其它領(lǐng)域的相控參量聲場(chǎng)研究也具有借鑒意義。

致謝：感謝水聲技術(shù)重點(diǎn)實(shí)驗(yàn)室紀(jì)祥春老師、田寶晶老師以及李磊老師在開(kāi)展水池實(shí)驗(yàn)過(guò)程中給予的大力支持和無(wú)私幫助。

［1］Olav R G，Kenneth G F，Johnny D，et al．Detecting atlantic herring by parametric sonar［J］．J．Acoust．Soc．Am，Express Letters，2010，127（4）：153－159．

［2］Egor V D，Bojan B G．Acoustic radiation force in tissue-like solids due to modulated sound field［J］．Journal of the Mechanics and Physics of Solids，2012，60：1791－1813．

［3］Akiyoshi I，Nobuo T，Hiroyuki I．Global active noise control using a delayed driving parametric array loudspeaker［J］．The Japan Society of Mechanical Engineers，2013，79（799）：604－617．

［4］Milan C，Michal B．Non-paraxialmodel for a parametric acoustic array［J］．J．Acoust．Soc．Am，2013，134（2）：933－938．

［5］Hideyuki N，Claes MH，Tomoo K．Numerical simulation of length-limited parametric sound beam［C］．International Congress on Ultrasonics，2012，1433：547－550．

［6］David G．B，Mark B M，William L K．Parametric acoustic array developmentat the USNavy's New London，Connecticut laboratory［C］．Acoustical Society of America，Physical A-coustics，2009，6：1－22．

［7］Karsten W，Thomas B，Tobias W．Parametric underwater communications［C］．11thEuropean Conference on Underwater Acoustics，2012，17：1－10．

［8］Akira A，TamakiU，F(xiàn)umitaka M，etal．Sub-bottom synthetic aperture imaging sonar system using an AUV and an autonomous surface tracking vehicle for searching for buried shells of toxic chemicals［C］．Waterside Security conference，2010，1－3．

［9］Maxim S，Tony W H S．Simulation of nonlinear westervelt equation for the investigation of acoustic streaming and nonlinear propagation effects［J］．J．Acoust．Soc．Am，2013，134（5）：3931－3942．

［10］楊德森，蘭朝鳳，時(shí)勝國(guó)，等．水中聲波非線性相互作用的聲吸收研究［J］．振動(dòng)與沖擊，2012，31（8）：52－56．

YANG De-sen，LAN Chao-feng，SHI Sheng-guo，et al．Sound absorption of sound under interaction among underwater nonlinear acoustic variable parameters［J］．Journal of Vibration and Shock，2012，31（8）：52－56．

［11］LIUWei，YANG Jun，TIAN Jing．Time-domain modeling of finite-amplitude sound beams in three-dimensional Cartesian coordinate system［J］．Chinese Journal of Acoustics，2012，31（4）：408－422．

［12］杜宏偉．生物醫(yī)學(xué)超聲中若干非線性問(wèn)題的研究［D］．合肥：中國(guó)科學(xué)技術(shù)大學(xué)，2007．

［13］Kenneth G F，David T IF，Philip R A．Calibration sphere for low-frequency parametric sonars［J］．J．Acoust．Soc．Am，2007，121（3）：1482－1490．

［14］Paul LMJvan N，MikhailG D，Martin D V，etal．Comparison of fundamental，second harmonic and superharmonic imaging：A simulation study［J］．J．Acoust．Soc．AM，2011，130（5）：3148－3157．

［15］Shi Chuang，Gan W S．Steerable parametric loudspeakerwith preprocessing methods［C］．Proceedings of Meetings on A-coustics，2013，19：1－6．

［16］李太寶．計(jì)算聲學(xué)－聲場(chǎng)的方程和計(jì)算方法［M］．北京：科學(xué)出版社，2005．

［17］Yang Jun，Sha Kan，Gan W S，etal．A fast field scheme for the parametric sound radiation from rectangular aperture source［J］．Chin．Phys．Lett，2004，21（1）：111－113．

［18］Aanonsen S I，Barkve T，Tj?tta J N，et al．Distortion and harmonic generation in the nearfield of a finite amplitude sound beam［J］．J．Acoust．Soc．Am，1984，75：749－768．

［19］Kaya O A，sahin A，Kaleci D．Pressure field of rectangular transducers at finite amplitude in three dimensions［J］．Ultrasound in Med．＆Biol，2006，32（2）：271－280．

［20］Egor V D，Bojan BG．On the KZK-type equation formodulated ultrasound fields［J］．Wave Motion，2013，50：763－775．

［21］Lee Y S．Numerical solution of the KZK equation for pulsed finite amplitude sound beams in thermoviscous fluids［D］．Texas：University of Texas，1993．

［22］MarcoMV．3D harmonic echocardiography［D］．Rotterdam：Erasmus University，2007．

［23］Lucilla D M，Jacques M，Pierre C．Nonlinearmulti-frequency generation for underwater application［J］．Applied Acoustic，2012，73：900－903．

［24］Kenneth BO，Leon A F．Sound field calculation for rectangular sources［J］．IEEE Transactions on Ultrasonics，1989，36（2）：242－248．

Modeling and experimental investigation on rectangular aperture parametric array phased nonlinear acoustic field

ZHU Jian-jun1，2，LIHai-sen1，2，WEIYu-kuo1，2，CHEN Bao-wei1，2，ZHOU Tian1，2
（1．Acoustic Science and Technology Laboratory，Harbin Engineering University，Harbin 150001，China；2．College of Underwater Acoustic Engineering，Harbin Engineering University，Harbin，150001，China）

In order to solve the problem of that phased nonlinear acoustic field could not bemodeled by one order parabolic approximation KZK equation，an equivalent parametric array primary frequency natural directivity acoustic field modelwas builtbased on the collimation characteristic of primary frequency acoustic field．The equivalent relation between this field and the primary frequency phased acoustic field was deduced，so the problem of phased nonlinear acoustic field modeling was transferred to the calculation of equivalent parametric array source condition，and an operator split time domain finite difference calculation method was derived．The rectangular aperture parametric array phased nonlinear field calculation based on KZK equation was realized．Taking the SES2000 parametric array acoustic field as object，the phased nonlinear acousticmodel and the corresponding field calculation method were examined by computer simulation and pool contrast experiment．

rectangular aperture parametric array；phased nonlinear acoustic field；acoustic field modeling

TB532；TB52+5

A

10．13465／j．cnki．jvs．2015．12．005

國(guó)家自然科學(xué)基金（41327004，41306182）；高等學(xué)校博士學(xué)科點(diǎn)專項(xiàng)科研基金（20112304130003）；中央高校基本科研業(yè)務(wù)費(fèi)（HEUCF140501）

2014－03－25 修改稿收到日期：2014－05－14

朱建軍 男，博士生，助教，1981年生

李海森 男，博士，教授，博士生導(dǎo)師，1962年生