解放CA141載重汽車驅動橋殼動態特性的有限元分析

庹前進

（湖南機電職業技術學院，長沙 410151）

0 引言

驅動橋橋殼是載重汽車的重要組成部分，其生產質量、性能將對車輛的整體性能和使用壽命產生直接影響。本文為了解決載重汽車驅動橋殼的安全性問題，根據有限元理論，以解放CA141載重車為例，我們對其驅動橋殼動態特性進行有限元分析。

1 建立橋殼幾何模型

首先我們在建立幾何模型前對實際結構進行一定的合理簡化和假設，這樣既能使模型盡量簡單，又可以使有限元模型能夠真實地反映實際幾何體的結構特征和重要力學特性。所建實體模型如圖1所示。

2 建立橋殼有限元模型

1）啟動 ANSYS Workbench/Simulation；

2）選擇 Geometry>From File；

3）將三維模型導入幾何模型所在的文件夾。

有限元模型如圖2所示。

圖1 橋殼幾何模型

3 確定載荷及邊界條件

3.1 計算驅動橋殼載荷

驅動橋殼在汽車行駛過程中主要承受的力有垂向力、切向力和側向力，受力狀況比較復雜。通常橋殼設計考慮四種載荷工況：

1）最大垂向力工況。條件滿足載重汽車滿載，受沖擊載荷的作用，最大垂向力為：ZL=2.5G×a2/（a1+a2）；ZR=2.5G×a1/（a1+a2）。代入實驗數據得ZL=ZR=98 600 N。

2）最大牽引力工況。條件滿足汽車滿載，最大牽引力為Pmax=Temaxig1i0ηT/rr。代入實驗數據得Pmax=78 635 N。

3）最大制動力工況。條件滿足汽車滿載，最大制動力大小為B=Gm′φ/2。式中：B為最大制動力；G為驅動橋給地面的載荷，為 78 885 N；m′一般取 0.75～0.95，取 0.85；φ為附著系數，計算時取0.8。代入實驗數據得B=25 245 N。

4）最大側向力工況。當汽車突發側滑時，驅動橋承受的側向力為Y=G×φ1。式中Y為側向力。代入實驗數據得Y=78 885 N。

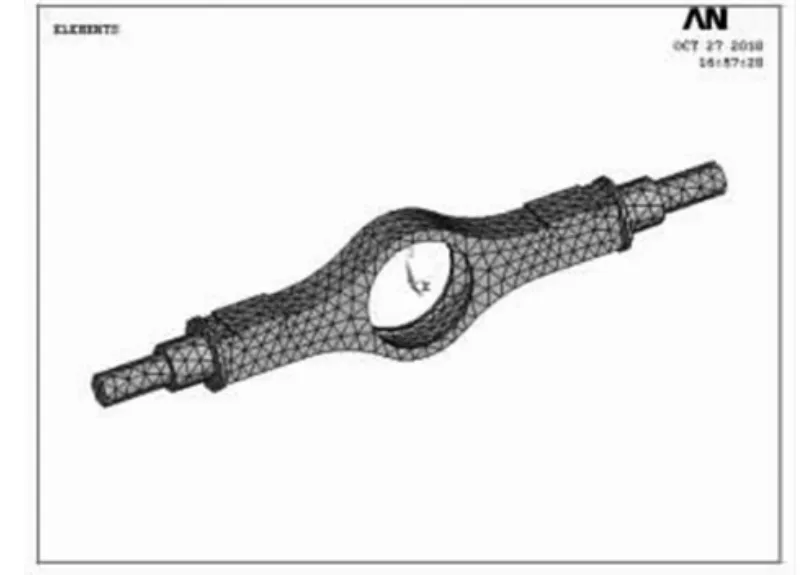
圖2 橋殼有限元模型

3.2 確定邊界條件

綜上所述，加載方式和約束條件如表1和表2所示。

表1 加載方式

表2 約束條件

4 計算結果及分析

4.1 最大垂向力工況

如圖3（a）所示，輪轂軸管滿足汽車行駛強度要求。同樣，從圖3（b）中我們也可以分析出，橋殼最大變形量滿足國家標準。

4.2 最大牽引力工況

等效應力分布和變形如圖4所示。

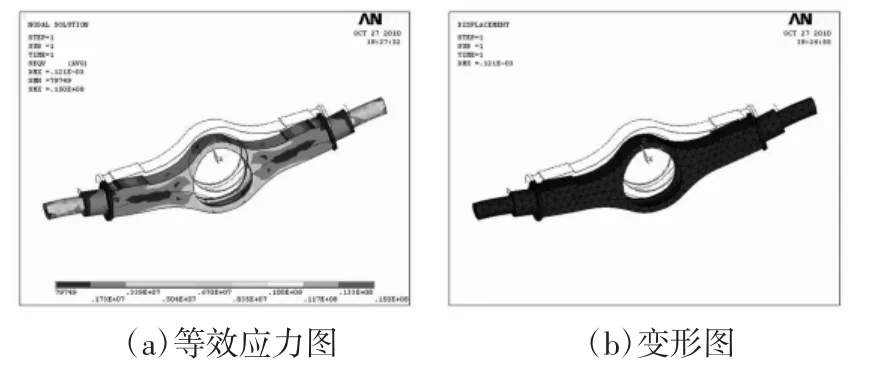
圖3 最大垂向力的等效應力及變形圖

如圖4（a）所示，各處強度分布比較合理。如圖4（b）所示，最大變形不超過1.5 mm/m的要求，滿足設計要求。

4.3 最大側向力工況

車橋橋殼的應力分布和變形如圖5所示。

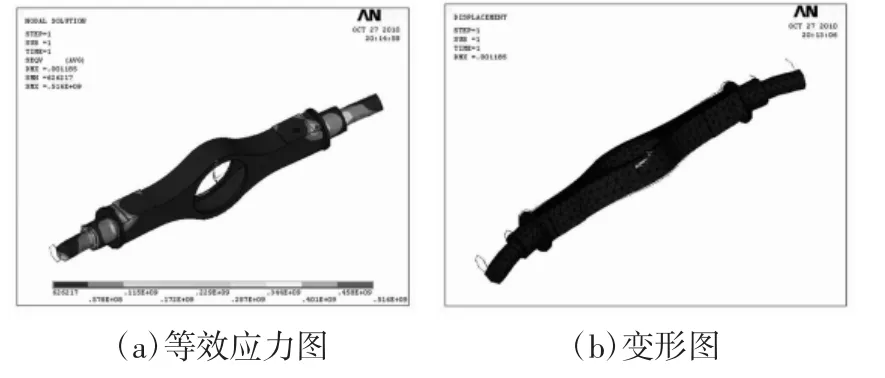
圖4 最大牽引力的等效應力及變形圖

由圖5可知，最大變形量出現在側滑方向一側輪轂軸管的端部，同樣符合國家標準。

圖5 最大側向力的等效應力及變形圖

5 結論

我們采用有限元法對解放CA141載重汽車驅動橋殼進行了實驗模態分析，主要考慮了汽車行駛狀態下的4種受力狀況，對解放CA141載重汽車車橋橋殼的結構設計及工作性能得出如下結論：橋殼的變形和應力分布合理，強度和剛度滿足使用要求，解放CA141載重汽車驅動橋殼在各種工作條件下是穩定可靠的。

［1］ 齊東東，孫桓五，齊麗麗，等．基于ANSYS的載重貨車驅動橋殼的結構強度與模態分析［J］．機械傳動，2012，36（8）：105-123．

［2］ 楊彥超，王鐵，張瑞亮．基于變截面的驅動橋殼結構優化［J］．機械傳動，2013，37（10）：94-97．

［3］ 葛劍敏，鄭聯珠．路面特性對車輛振動影響規律研究［J］．中國公路學報，2004，17（3）：117-121．