含摩擦碰撞柔性機(jī)械臂動力學(xué)研究

錢震杰， 章定國

(南京理工大學(xué)理學(xué)院， 江蘇 南京 210094)

含摩擦碰撞柔性機(jī)械臂動力學(xué)研究

錢震杰， 章定國

(南京理工大學(xué)理學(xué)院， 江蘇 南京 210094)

研究了由柔性桿、柔性鉸構(gòu)成的機(jī)械臂的斜碰撞動力學(xué)問題。首先，采用高次剛?cè)狁詈侠碚摗?yīng)用Lagrange方程得到系統(tǒng)的遞推動力學(xué)模型。然后，引入碰撞力勢能，運(yùn)用連續(xù)法建模獲得碰撞力所對應(yīng)的廣義力，得到系統(tǒng)的碰撞動力學(xué)方程。采用Hertz接觸模型和Coulomb摩擦光滑修正模型分別建立法向和切向碰撞模型，提出碰撞/分離切換準(zhǔn)則。通過光滑化處理摩擦接觸，提高了大型復(fù)雜柔性多體系統(tǒng)含摩擦碰撞全局動力學(xué)的計(jì)算效率。最后對國際空間站機(jī)械臂Canadarm2的簡化模型斜碰撞過程進(jìn)行仿真，驗(yàn)證了所提模型和算法的有效性。

斜碰撞； 摩擦； 柔性多體系統(tǒng)； 動力學(xué)仿真

引 言

摩擦與碰撞振動是導(dǎo)致大型柔性機(jī)構(gòu)動力學(xué)非光滑、高度非線性問題的主要因素。柔性多體系統(tǒng)變形描述、接觸模型、stick-slip現(xiàn)象分析、接觸/分離切換、碰撞檢測、以及碰撞算法等都是研究的重點(diǎn)和難點(diǎn)。

針對多體系統(tǒng)的碰撞模型問題，Whittaker[1]最早對多剛體系統(tǒng)的斜碰撞進(jìn)行研究，提出單向滑動和黏滯兩種接觸模式，利用Coulomb摩擦定律描述法向和切向沖量之間的關(guān)系。Kane[2]發(fā)現(xiàn)前者方法會導(dǎo)致碰撞后系統(tǒng)能量的增加，提出Kane 動力學(xué)之謎。研究發(fā)現(xiàn)：該現(xiàn)象出現(xiàn)的主要原因是忽略了切向滑動方向轉(zhuǎn)換和黏滯帶來的摩擦力大小、方向的變化。Stronge[3]以自由物體與平面斜碰撞為對象分析了斜碰撞過程的能量變化及碰撞前后速度關(guān)系，建立了黏滯/滑動摩擦接觸的動力學(xué)模型。Brach[4]和Keller[5]研究了斜碰撞中切向微滑動，以及法向變形與切向變形的同步和耦合關(guān)系。Glocker 和Pfeiffer[6]基于Poisson假設(shè)建立了多剛體系統(tǒng)的含摩擦多點(diǎn)碰撞模型，研究了不同接觸狀態(tài)的切換問題。趙振[7]等針對三維含摩擦的多剛體碰撞問題，以Poisson恢復(fù)系數(shù)判斷碰撞狀態(tài)，分析了切向運(yùn)動和法向沖量的耦合關(guān)系。劉才山等[8]針對柔性單桿碰撞問題，提出了滿足邊界條件的法向非線性彈簧阻尼模型和切向接觸模型。劉錦陽等[9]運(yùn)用Hertz接觸和Coulomb摩擦定律建立法向和切向碰撞模型，研究了柔性梁斜碰撞問題。閻紹澤等[10]建立了含間隙空間可展機(jī)構(gòu)考慮經(jīng)典碰撞和接觸變形的動力學(xué)模型，并分析比較了四類間隙鉸模型。齊朝暉等[11]對多體系統(tǒng)鉸內(nèi)摩擦接觸問題進(jìn)行了詳細(xì)研究。胡海巖等[12]對大型網(wǎng)架式空間結(jié)構(gòu)展開過程中的多柔體系統(tǒng)動力學(xué)建模、運(yùn)動副內(nèi)碰撞等非線性動力學(xué)問題進(jìn)行了詳細(xì)的分析和總結(jié)。

根據(jù)不同的碰撞過程假設(shè)，目前含碰撞非光滑系統(tǒng)的建模主要有沖量-動量法、連續(xù)碰撞力法、附加約束法等。連續(xù)碰撞力法是一種以彈簧阻尼力元代替接觸區(qū)域復(fù)雜變形的近似方法。此法不僅解決了剛性碰撞理論中切向摩擦引起的數(shù)值不穩(wěn)定和能量不一致問題，而且能簡易地求解撞擊力，碰撞速度以及接觸時(shí)間等。雖然其計(jì)算結(jié)果的準(zhǔn)確性受到模型參數(shù)選擇的影響，但在處理低速碰撞時(shí)仍有較高的精度，因此在航天器對接等領(lǐng)域廣泛應(yīng)用。Khulief和Shabana[13]將線性彈簧阻尼模型引入到多體系統(tǒng)碰撞動力學(xué)的研究中。王琪等[14]針對多剛體系統(tǒng)研究了雙面約束多點(diǎn)摩擦問題，總結(jié)了非光滑多體系統(tǒng)動力學(xué)的數(shù)值算法[15]。姚文莉等[16]提出一種滑動模式步進(jìn)算法，解決含鉸摩擦的多剛體系統(tǒng)的碰撞前后能量不協(xié)調(diào)問題。金棟平等[17]基于步進(jìn)沖量法，深入研究了兩彈性體含摩擦斜碰撞中的法向壓縮/恢復(fù)、切向微滑正向/逆向等問題。洪嘉振等[18]詳細(xì)總結(jié)了柔性多體系統(tǒng)碰撞動力學(xué)建模理論、數(shù)值算法和實(shí)驗(yàn)方面的進(jìn)展情況。

常規(guī)數(shù)值方法處理含摩擦接觸的非光滑系統(tǒng)時(shí)，存在降階和精度較低的問題，黏滯時(shí)數(shù)值易發(fā)生不穩(wěn)定。為此學(xué)者們提出了光滑化方法[19]、黏著區(qū)判斷法[20]、事件驅(qū)動法[21]等解決方案。其中光滑化方法將不可微的函數(shù)轉(zhuǎn)化為一個(gè)可微函數(shù)，利用反正切、雙曲正切或樣條函數(shù)等光滑函數(shù)逼近干摩擦定律，進(jìn)而采用一般的光滑優(yōu)化算法求解。此法無需額外方程或變量，通過適當(dāng)?shù)墓饣幚恚鉀Q了模型奇異性導(dǎo)致的數(shù)值不穩(wěn)定問題，起到了平滑振蕩的數(shù)值效果。雖然此法有一定的近似性，但如將光滑化參數(shù)取得足夠小，便可得到充分精確的解。因此，光滑化方法不失為一種工程應(yīng)用的有效方法。 Kikuchi[22]和Wriggers等[23]研究了光滑化接觸算法，給出了插值函數(shù)。Mostaghel 和Davis[24]提出了運(yùn)用4種連續(xù)函數(shù)分段近似描述摩擦力的建模方法。李興斯等[25]基于凝聚函數(shù)法的光滑化技術(shù)研究了摩擦接觸問題。

針對柔性多體系統(tǒng)的含摩擦碰撞問題，需要解決碰撞、摩擦引起的變邊界、高瞬態(tài)、數(shù)值穩(wěn)定性問題，因此建立數(shù)值性能較好、合理的接觸模型和算法至關(guān)重要。本文采用高次剛?cè)狁詈侠碚摻⑷嵝远囿w系統(tǒng)動力學(xué)模型。通過Lagrange方程得到遞推動力學(xué)方程。引入碰撞力勢能的概念，通過連續(xù)法建模得到碰撞動力學(xué)方程。采用Hertz接觸模型建立法向接觸模型，給出切向Coulomb摩擦的光滑修正模型，以及碰撞/分離切換準(zhǔn)則。最后對國際空間站機(jī)械臂Canadarm2的簡化模型斜碰撞問題進(jìn)行了仿真分析。

1 動力學(xué)方程

柔性機(jī)械臂由n個(gè)柔性桿和n個(gè)轉(zhuǎn)動鉸構(gòu)成(見圖1)。設(shè)基座坐標(biāo)系為O-XYZ，碰撞面ΓB坐標(biāo)系為O'-X'Y'Z'。運(yùn)用4×4齊次變換矩陣和Denavit-Hartenberg (D-H)坐標(biāo)法來描述系統(tǒng)的運(yùn)動和變形。

圖1 柔性機(jī)器人碰撞示意圖Fig.1 The flexible system collision schematic

柔性機(jī)械臂桿k上一點(diǎn)P與接觸面ΓB發(fā)生點(diǎn)-面碰撞接觸。點(diǎn)P在基座坐標(biāo)系O-XYZ中表示為

hk=Wkkhk

(1)

式中Wk為基座坐標(biāo)系到第k桿坐標(biāo)系的齊次變換矩陣，khk表示點(diǎn)P在k桿連體坐標(biāo)系中的位置矢量，

(2)

(3)

(4)

式中xkj,ykj,zkj分別表示k桿的x,y,z三個(gè)方向的第j階模態(tài)的變形位移，Nk為第k桿的模態(tài)截?cái)鄶?shù)，δkj為桿k的第j階模態(tài)坐標(biāo)，xkjf表示由橫向彎曲引起的軸向縮短項(xiàng)，即高階幾何非線性耦合項(xiàng)，下劃線項(xiàng)表示高次耦合項(xiàng)或由其產(chǎn)生的導(dǎo)出項(xiàng)。

采用連續(xù)接觸力法建立碰撞過程模型，引入碰撞力勢能

(5)

進(jìn)入碰撞階段后，由于碰撞力強(qiáng)度大且變化劇烈，迅速激發(fā)高頻模態(tài)，動力學(xué)方程易不穩(wěn)定，求解步長需要縮小，求解速度明顯下降。因此，問題的多尺度性和非連續(xù)性要求系統(tǒng)的耦合變形描述和方程數(shù)值求解有更高的精度。這里，柔性桿為細(xì)長桿，采用Euler-Bernoull梁假設(shè)，考慮軸向拉伸變形、軸向高階幾何非線性耦合變形、橫向彎曲變形、以及扭轉(zhuǎn)變形；鉸計(jì)入柔性和質(zhì)量效應(yīng)。

運(yùn)用第二類Lagrange方程描述系統(tǒng)含摩擦的斜碰撞過程，歸納總結(jié)得到非碰撞階段和碰撞階段的動力學(xué)方程分別為：

(6)

(7)

式中J為系統(tǒng)的廣義質(zhì)量陣，RI為除碰撞力外的所有主動力、部分慣性力產(chǎn)生的廣義力，z為廣義坐標(biāo)列陣，見文獻(xiàn)[26]。通過碰撞力勢能，求得對應(yīng)的碰撞廣義力RII為：

(8)

(9)

(10)

2 接觸模型

針對多體系統(tǒng)斜碰撞動力學(xué)問題，學(xué)者們對切向摩擦、法向接觸是否同步和耦合關(guān)系進(jìn)行了大量研究。Johnson[27]認(rèn)為切向變形對法向變形的影響很小，尤其是當(dāng)碰撞物體的材料相同時(shí)，切向變形的影響甚微，即正碰撞的法向撞擊力模型適用于斜碰撞問題。Lewis和Rogers的研究[28]表明，對單向微滑動而言，斜碰撞過程中法向與切向碰撞力的時(shí)間變化歷程是同步的。目前現(xiàn)有的研究中，通常認(rèn)為切向摩擦系數(shù)與法向恢復(fù)系數(shù)是相互獨(dú)立的。

2.1 法向接觸模型

在Hertz接觸理論和非線性彈簧阻尼模型[29]的基礎(chǔ)上，Lankarani-Nikravesh建立了L-N連續(xù)接觸力模型[30]，提出通過物體碰撞前后動能損失來確定接觸阻尼，其法向碰撞力與變形的非線性關(guān)系為

(11)

2.2 切向摩擦模型

系統(tǒng)摩擦所產(chǎn)生的stick-slip涉及動摩擦和靜摩擦狀態(tài)的切換，經(jīng)典庫侖摩擦定律將引起數(shù)值困難。在不考慮系統(tǒng)的stick-slip運(yùn)動狀態(tài)切換時(shí)，即不考慮摩擦的靜態(tài)特性時(shí)，可以將切向摩擦力光滑化處理，把黏滯階段處理為一個(gè)相對速度為零的小鄰域，去掉表征摩擦力方向的符號函數(shù)。修正之后摩擦力僅與相對切向速度有關(guān)，與相對切向加速度無關(guān)。

聯(lián)邦、州和地方多個(gè)部門設(shè)立基金和針對再生水資金支持項(xiàng)目計(jì)劃的外生融資主要用于項(xiàng)目建設(shè)，運(yùn)行維護(hù)和更替費(fèi)用則主要依賴使用費(fèi)、物業(yè)稅、用戶付費(fèi)、公共設(shè)施稅收返還、特種稅、增容費(fèi)等收入渠道的內(nèi)生融資體系。這使得再生水項(xiàng)目在得到必要外部支持的同時(shí)，通過努力改善經(jīng)營而獲得充足的收入。由于原則上要求用戶承擔(dān)全部運(yùn)營更替成本，其內(nèi)生融資的費(fèi)率體系充分體現(xiàn)了清晰的商業(yè)原則。

(12)

式中cf為摩擦系數(shù)，cd為一個(gè)動態(tài)的校正系數(shù)，是關(guān)于vT的分段函數(shù)。這里考慮3種摩擦修正模型，具體情況如下：

Ⅰ.Coulomb摩擦分段函數(shù)模型[31]：為解決摩擦力方向改變后出現(xiàn)切向速度為空值的問題，將動態(tài)校正因子cd視為關(guān)于切向速度公差的函數(shù)

(13)

式中 兩個(gè)臨界速度v0,v1為常值，當(dāng)相對切向速度的絕對值在0～v0范圍內(nèi)時(shí)，摩擦力為零，接觸處于粘滯狀態(tài)；其值在v0～v1范圍內(nèi)時(shí)，靜摩擦系數(shù)隨之變化；其值大于v1時(shí)，接觸處于滑動狀態(tài)。

Ⅱ. 近似Coulomb摩擦光滑模型[31]：此模型避免了摩擦力與相對切向加速度的耦合給數(shù)值計(jì)算帶來的困難

(14)

其中cT為切向碰撞恢復(fù)系數(shù)，vr1,α為大于0 的常值，α的值越大，曲線越陡。

Ⅲ. 1902年Stribeck觀察到：當(dāng)克服靜摩擦力后摩擦力不是連續(xù)地下降，而是在低速下隨著速度的增加而減小，呈現(xiàn)為速度的連續(xù)函數(shù)，即負(fù)斜率摩擦現(xiàn)象。這里，考慮Stribeck效應(yīng)的近似Coulomb摩擦模型[32]

(15)

其中

(16)

(17)

2.3 狀態(tài)切換準(zhǔn)則及算法實(shí)現(xiàn)

柔性機(jī)械臂桿k上一點(diǎn)P與接觸面ΓB發(fā)生點(diǎn)-面碰撞接觸，如圖2所示。WB為基座坐標(biāo)系至接觸面ΓB坐標(biāo)系的齊次變換矩陣，rk表示接觸點(diǎn)Q在接觸面ΓB坐標(biāo)系中的位置矢量。

圖2 點(diǎn)-面碰撞接觸示意圖Fig.2 The node-to-surface collision schematic

因此，接觸對法向和切向距離gN和gT為：

(18)

(19)

(20)

(21)

(22)

(23)

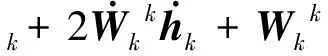
(24)

(25)

3 數(shù)值仿真

圖3 空間機(jī)械臂Canadarm2簡化模型Fig.3 A simplified model of Canadarm2

表1 機(jī)械臂柔性桿參數(shù)

由程序?qū)崟r(shí)計(jì)算得到，碰撞初始速度為vx=-0.516 46 m/s,vy=-6.401 82 m/s,vz=-0.003 78 m/s。

在第 Ⅰ 種Coulomb摩擦分段函數(shù)模型中：摩擦系數(shù)cf=0.1，校正系數(shù)cd中常數(shù)參數(shù)v0=0.001 m/s，v1=0.05 m/s。法向碰撞力和切向滑動速度由程序?qū)崟r(shí)計(jì)算獲得。圖4是碰前桿2末端加速度。

圖4 碰前桿2末端加速度Fig.4 Acceleration of Link-2 tip before impact

在碰撞前，隨著運(yùn)動速度的增加，沿桿連體坐標(biāo)系x向和z向振動幅值較小，而沿y向由于考慮了高階剛?cè)狁詈献冃雾?xiàng)，振動幅值較大。

圖5 法向碰撞力和切向碰撞力Fig.5 The normal and the tangential impact forces

法向碰撞力和切向摩擦力如圖5所示。在tstart=0.646 663s碰撞開始，結(jié)束時(shí)間tend=0.650 660s，持續(xù)時(shí)間為0.003 997s。在1次碰撞內(nèi)有3次法向和切向沖擊力峰值，碰撞激發(fā)柔性構(gòu)件的高次剛?cè)狁詈险駝樱?次碰撞內(nèi)發(fā)生多次顫振。圖6是碰撞中桿2末端變形量，顯見沖擊力使得柔性桿變形量超過20%，達(dá)到大變形狀態(tài)。圖7是碰撞中桿2末端變形速度。沿桿連體坐標(biāo)系y向的振幅峰值與沖擊力3次峰值一一對應(yīng)。

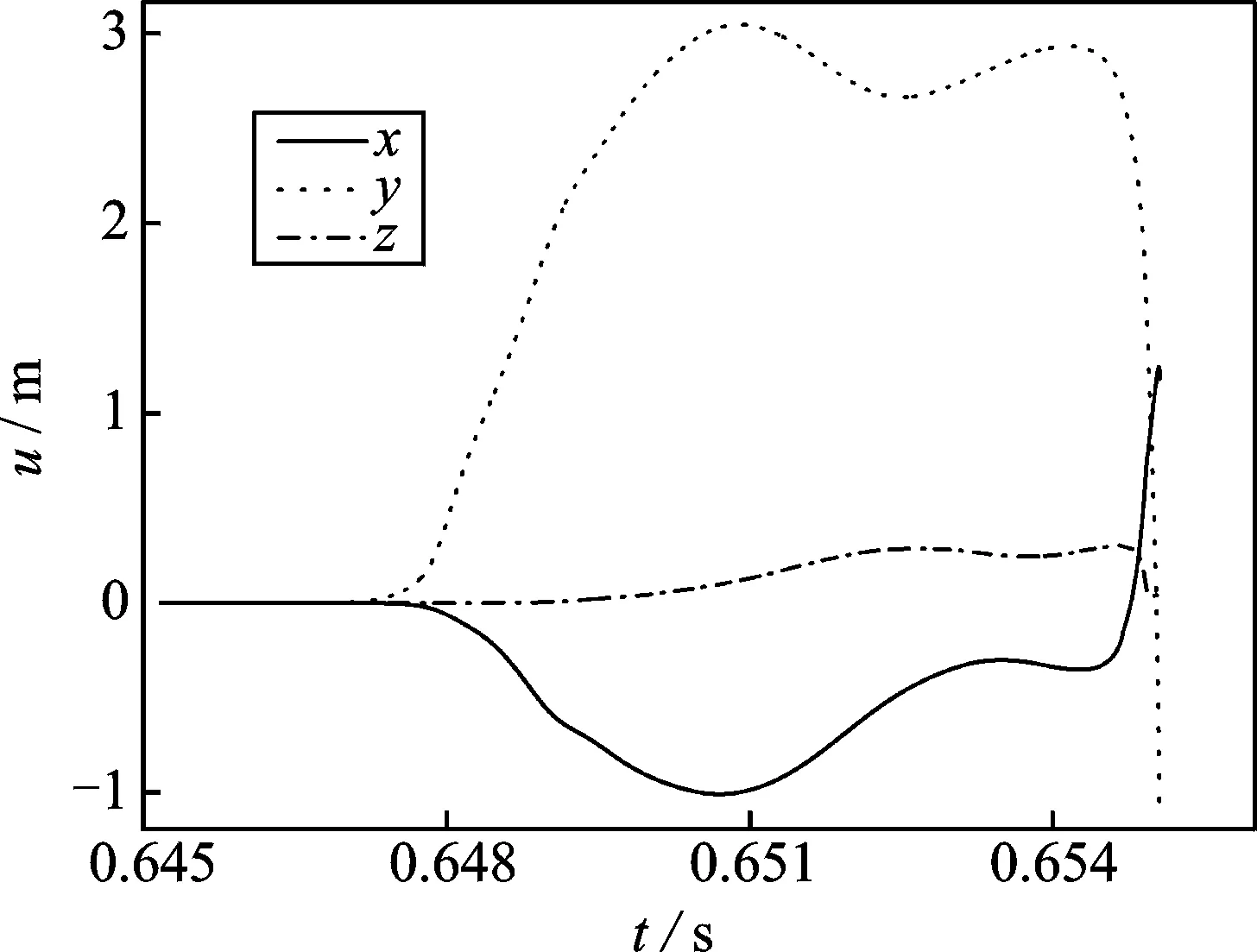
圖6 碰撞中桿2末端的變形量Fig.6 Deformation at Link-2 tip during impact

圖7 碰撞中桿2末端的變形速度Fig.7 Deformation speed of Link-2 tip during impact

圖8 碰撞中接觸點(diǎn)切向速度Fig.8 Tangential velocity of contact point

在第Ⅲ種考慮Stribeck效應(yīng)的近似Coulomb摩擦模型中：靜、動摩擦臨界速度為vs=0.04 m/s,vd=0.05 m/s，靜、動摩擦系數(shù)為μs=0.95,μd=0.85。法向碰撞力和切向滑動速度由程序?qū)崟r(shí)計(jì)算獲得。通過仿真可以得到，碰撞開始時(shí)間為tstart=0.646 663 s，結(jié)束時(shí)間為tend=0.650 203 s，持續(xù)時(shí)間為0.003 540s。法向沖擊力和切向摩擦力如圖9所示。在1次碰撞過程中，切向和法向沖擊力形成3次峰值，一次碰撞內(nèi)發(fā)生多次顫振。圖10 為碰撞中桿1末端變形加速度。在重力場中，柔性系統(tǒng)的高階耦合變形和碰撞激發(fā)了柔性構(gòu)件的劇烈振動響應(yīng)。

圖9 法向碰撞力、切向碰撞力Fig.9 The normal and tangential impact forces

圖10 碰撞中桿1末端加速度Fig.10 Acceleration of Link-1 tip during collision

4 結(jié) 論

本文研究了柔性機(jī)械臂系統(tǒng)的含摩擦斜碰撞動力學(xué)問題。采用高次剛?cè)狁詈侠碚撏ㄟ^Lagrange方程得到系統(tǒng)的遞推動力學(xué)模型。引入碰撞力勢能，連續(xù)法處理碰撞狀態(tài)，光滑化處理摩擦接觸，提高了柔性多體碰撞動力學(xué)的計(jì)算精度。數(shù)值仿真表明，碰撞力激發(fā)了柔性桿變形的高階振動模態(tài)；在一次碰撞過程中，發(fā)生了多次碰撞，滑動摩擦力多次發(fā)生正、逆向的改變。通過連續(xù)法處理碰撞過程以及光滑化處理摩擦接觸，縮短了已有非光滑力學(xué)理論與工程實(shí)際應(yīng)用之間的距離，提高了大型復(fù)雜柔性多體系統(tǒng)含摩擦碰撞的全局動力學(xué)的計(jì)算效率。

[1] Whittaker E T. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies[M]. 4th ed.Cambridge: University Press, London 1937 Reprinted by Dover Publications, New York 1944.

[2] Kane T R. A dynamics puzzle[J]. Stanford Mechanics Alumni Club Newsletter, 1984, 6: 1—4.

[3] Stronge W J, James R, Ravani B. Oblique impact with friction and tangential compliance[J]. Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 2001, 359(1789): 2 447—2 465.

[4] Brach R M. Rigid body collisions[J]. Journal of Applied Mechanics, 1989, 56(1): 133—138.

[5] Keller J B. Impact with friction[J]. Journal of Applied Mechanics, 1986, 53(1): 1—4.

[6] Glocker C, Pfeiffer F. Multiple impacts with friction in rigid multibody systems[J]. Nonlinear Dynamics, 1995, 7(4): 471—497.

[7] Zhao Zhen, Liu Caishan, Chen Bin.The numerical method for three-dimensional impact with friction of multi-rigid-body system[J].Science in China Series G, 2006, 49(1): 102—118.

[8] 劉才山,陳濱,王玉玲.考慮摩擦作用的多柔體系統(tǒng)點(diǎn)-面碰撞模型[J]. 中國機(jī)械工程, 2000, 11(6): 616—619.

Liu Caishan, Chen Bin, Wang Yuling. The point-surface impact model considering the friction effect in flexible multi-body system [J].China Mechanical Engineering, 2000, 11(6): 616—619.

[9] 沈凌杰, 劉錦陽, 余征躍. 柔性梁斜碰撞問題的非線性動力學(xué)建模和實(shí)驗(yàn)研究[J]. 力學(xué)季刊, 2007, 27(4): 568—577.

Shen Lingjie, Liu Jinyang, Yu Zhengyue. Nonlinear dynamic modeling and experiment investigation for a flexible beam with oblique impact[J]. Chinese Quartrtly of Mechanics, 2007, 27(4): 568—577.

[10]閻紹澤，陳鹿民，季林紅，等.含間隙鉸的機(jī)械多體系統(tǒng)動力學(xué)模型[J]. 振動工程學(xué)報(bào), 2003, 16(3): 290—294.

Yan Shaoze, Chen Lumin, Ji Linhong, et al. Dynamic modeling of multibody system with clearance joints[J]. Journal of Vibration Engineering, 2003, 16(3): 290—294.

[11]齊朝暉, 羅曉明, 黃志浩. 多體系統(tǒng)中典型鉸的摩擦力計(jì)算模型[J]. 動力學(xué)與控制學(xué)報(bào), 2008, 6(4): 294—300.

Qi Zhaohui, Luo Xiaoming, Huang Zhihao. Frictions in joints of multibody systems[J]. Journal of Dynamics and Control, 2008, 6(4): 294—300.

[12]胡海巖, 田強(qiáng), 張偉, 等. 大型網(wǎng)架式可展開空間結(jié)構(gòu)的非線性動力學(xué)與控制[J]. 力學(xué)進(jìn)展, 2013, 43(4): 390—414.

Hu Haiyan, Tian Qiang, Zhang Wei, et al. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes[J]. Advances in Mechanics, 2013, 43(4): 390—414.

[13]Khulief Y A, Shabana A A. A continuous force model for the impact analysis of flexible multibody systems[J]. Mechanism and Machine Theory, 1987, 22(3): 213—224.

[14]彭慧蓮, 王士敏, 王琪, 等. 雙面約束多點(diǎn)摩擦多體系統(tǒng)的建模和數(shù)值方法[J]. 力學(xué)學(xué)報(bào), 2009, 41(1): 105—112.

Peng Huilian, Wang Shimin, Wang Qi, et al. Modeling and simulation of multi-body systems with multi-friction and fixed bilateral constraint[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(1): 105—112.

[15]王琪, 莊方方, 郭易圓, 等. 非光滑多體系統(tǒng)動力學(xué)數(shù)值算法的研究進(jìn)展[J]. 力學(xué)進(jìn)展, 2013, 43(1): 101—111.

Wang Qi, Zhuang Fangfang, Guo Yiyuan, et al. Advances in the research on numerical methods for non-smooth dynamics of multibody systems[J]. Advances in Mechanics, 2013, 43(1): 101—111.

[16]姚文莉, 陳濱, 劉才山, 等. 含摩擦的多剛體系統(tǒng)碰撞問題的滑動狀態(tài)步進(jìn)法[J]. 應(yīng)用數(shù)學(xué)和力學(xué), 2007, 28(12): 1 448—1 454.

Yao Wenli, Chen Bin, Liu Cai-shan, et al. Sliding state stepping algorithm sloving impact problems of multi-rigid-body system with joint friction[J].Applied Mathematics and Mechanics, 2007, 28(12): 1 448—1 454.

[17]韓維,金棟平,胡海巖.兩自由度斜碰撞-振動系統(tǒng)動力學(xué)研究[J].力學(xué)學(xué)報(bào),2003,35(6): 723—728.

Han Wei, Hu Haiyan, Jin Dongping. Analysis of oblique impact of a vibrating system of two degrees of freedom[J]. Acta Mechanica Sinica, 2003, 35(6): 723—728.

[18]董富祥, 洪嘉振. 多體系統(tǒng)動力學(xué)碰撞問題研究綜述[J]. 力學(xué)進(jìn)展, 2009, 39(3): 352—359.

Dong Fuxiang, Hong Jiazhen. Review of impact problem for dynamics of multibody system[J]. Advances in Mechanics, 2009, 39(3): 352-359.

[19]Kim T C, Rook T E, Singh R. Effect of smoothening functions on the frequency response of an oscillator with clearance non-linearity[J].Journal of Sound and Vibration, 2003, 263(3): 665—678.

[20]Olsson H, ?str?m K J, Canudas de Wit C, et al. Friction models and friction compensation[J]. European Journal of Control, 1998, 4(3): 176—195.

[21]張繼鋒, 馮奇. 摩擦動力系統(tǒng)中兩種非光滑現(xiàn)象及其算法研究[J]. 噪聲與振動控制, 2007, 27(5): 38—41.

Zhang Jifeng, Feng Qi. Two kinds of non-smooth phenomena in a friction dynamical system and computational methods[J]. Noise and Vibration Control, 2007, 27(5): 38—41.

[22]Kikuchi N. A smoothing technique for reduced integration penalty method in contact problems[J]. International Journal for Numerical Methods in Engineering, 1982; 18:343—350.

[23]Wriggers P, Krstulovic-Opara L, Korelc J. Smooth C-1 interpolations for two-dimensional frictional contact problems[J]. International Journal for Numerical Methods in Engineering 2001, 51(12):1 469—1 495.

[24]Mostaghel N, Davis T. Representations of coulomb friction for dynamic analysis[J]. Earthquake Engineering and Structural Dynamics, 1997, 26(5): 541—548.

[25]宣兆成, 李興斯. 接觸分析的光滑模型及迭代算法[J]. 力學(xué)學(xué)報(bào), 2001, 33(3): 340—348.

Xuan Zhaocheng, Li Xingsi. Smooth model and iteration algorithm for contact analysis[J]. Acta Mechanica Sinica, 2001, 33(3): 340—348.

[26]Zhenjie Qian, Dingguo Zhang, Liu Jun. Recursive formulation for dynamic modeling and simulation of multilink spatial flexible robotic manipulators[J].Advances in Mechanical Engineering, Volume 2013(2013), Article ID 216014, 15.

[27]Johnson K L. Contact Mechanics[M]. Cambridge: Cambridge University Press, 1985.

[28]Lewis A D, Rogers R J. Experimental and numerical study of forces during oblique impact[J]. Journal of Sound and Vibration, 1988, 125(3): 403—412.

[29]Hunt K H, Crossley F R E. Coefficient of restitution interpreted as damping in vibroimpact[J]. Journal of Applied Mechanics, 1975, 42(2): 440—445.

[30]Lankarani H M, Nikravesh P E. A contact force model with hysteresis damping for impact analysis of multibody systems[J]. Journal of Mechanical Design, 1990, 112(3): 369—376.

[31]Flores P, Ambrósio J, Claro J C P, et al. Kinematics and Dynamics of Multibody Systems with Imperfect Joints: Models and Case Studies[M]. Springer-Verlag, Berlin Heidelberg, 2008.

[32]虞磊, 趙治華, 任啟鴻, 等. 基于絕對節(jié)點(diǎn)坐標(biāo)的柔性體碰撞仿真[J]. 清華大學(xué)學(xué)報(bào)(自然科學(xué)版), 2010, 50(7): 1 135—1 140.

Yu Lei, Zhao Zhihua, Ren Qihong, et al. Contact simulations of flexible bodies based on absolute nodal coordinates[J]. Journal Tsinghua University (Sci & Tech), 2010,50(7):1 135—1 140.

[33]Nguyen P K, Hughes P C. Teleoperation: from the space shuttle to the space station [J]. Progress in Astronautics and Aeronautics, 1994, 161:353—410.

Frictional impact dynamics of flexible manipulator arms

QIANZhen-jie,ZHANGDing-guo

(School of Science, Nanjing University of Science and Technology, Nanjing 210094, China)

In this paper, frictional impact dynamics is proposed for the flexible manipulator arms with high-order rigid-flexible coupling effect. Firstly, the system here is an assembly ofnflexible links connected bynrotary joints. All link flexibility, namely transversal, longitudinal, torsional and high-order flexible-rigid coupling deformation are included in this model. The 4×4 homogeneous transformation matrices are used to describe the kinematics of system and the recursive strategy for kinematics is adopted. Secondly, the contact/detachment is developed in a consistent manner by introducing the concept of impact force potential energy. The Hertz contact model is utilized to obtain the normal impact force. The tangential impact force is carried out in a smooth processing by modified Coulomb’s friction laws. The continue approach for contact/detachment and smoothed contact model are implemented as an explicit formulation which is suitable for real-time applications and improving the global dynamics computational efficiency for complex multi-body systems with frictional impact. Finally, a simplified model of Canadarm2 is illustrated to demonstrate the accuracy and efficiency of the presented approach and algorithms.

oblique impact; friction; flexible multi-body system; dynamics simulation

2014-08-29；

2015-05-12

國家自然科學(xué)基金資助項(xiàng)目(11272155, 11132007)；江蘇省“333”工程資助項(xiàng)目(BRA2011172)；中央高校基本科研業(yè)務(wù)費(fèi)專項(xiàng)資金資助項(xiàng)目(30920130112009)

O313; O322

A

1004-4523(2015)06-0879-08

10.16385/j.cnki.issn.1004-4523.2015.06.004

錢震杰 (1985—)，女，博士研究生。E-mail: qianzhenjie19851125@gmail.com

章定國(1967—)，男，教授。電話: (025)84315185；E-mail: zhangdg419@njust.edu.cn