一種基于自適應RSSI測距模型的無線傳感器網絡定位方法*

楊文鉑,邢鵬康,劉彥華

(河南工業職業技術學院電子工程系,河南 南陽 473000)

?

一種基于自適應RSSI測距模型的無線傳感器網絡定位方法*

楊文鉑,邢鵬康,劉彥華*

(河南工業職業技術學院電子工程系,河南 南陽 473000)

為了提高無線傳感器網絡的節點定位精度和環境適應性,研究了環境因素及信道噪聲對無線信號傳輸特性的影響,對測量誤差進行修正,得到精確的環境自適應RSSI測距模型,在此基礎上結合距離加權修正的改進WELSE算法,得到了一種新的混合定位算法。在ZigBee平臺CC2430上的測試結果表明本算法在未知環境中不需要預整定模型參數,在定位精度上,本文算法相比WELSE提高了49%,比WCLA提高了36%,可見其具備優秀的環境適應性和較高的定位精度。

WSN;節點定位;RSSI測距;環境自適應;WELSE

在無線傳感器網絡(WSN)應用中,節點的位置信息很重要,在大量的應用中,不知道傳感器節點位置的感知數據是沒有意義的。WSN的定位算法按其實現方式可分為基于外部實現的和基于自身實現的兩類。其于外部實現的是指需要WSN外的GPS、人工等輔助獲取坐標的方法;基于自身實現的定位是指其定位過程完全在內部完成。基于外部實現定位的方法,定位區域有一定局限性。為了獲得更好的適應性,基于WSN自身實現的定位方法成為必然的選擇。WSN內的節點按位置關系可分為定位節點和錨節點。定位節點(Blind Node)即待確定坐標的節點,可以是固定的也可以是移動的;錨節點又稱之為參考節點(RefNode),是固定好位置并預設好坐標的節點。基于WSN自身實現的定位算法主要是利用定位節點與錨節點的相對位置關系,根據錨節點的坐標計算出定位節點的實際坐標,這個過程一般需要多個錨節點參與。根據定位算法是否依據測量到錨節點的距離或角度分為:距離相關(range-based)的定位算法和距離無關(range-free)的定位算法[1]。前者較有代表性的是極大似然估計算法，后者較有代表性的是質心算法。通常距離較遠的錨節點信息對定位貢獻的誤差較大,距離較近的錨節點誤差較小。為使定位獲得較高的精度,偏向于較近節點提供的位置信息,需要引入距離權值來修正上述算法。對質心算法,引入修正后變為加權質心算法(WCLA)[2],實質上演變為距離相關算法。極大似然估計法引入修正后成為加權極大似然估計算法(WELSE)[3]。上述算法雖然原理不盡相同,但在定位過程中都需要準確的測距模型來提供定位計算的距離參數。距離相關定位算法需要利用TDOA或TOA、AOA[4]、無線信號強度指示(RSSI)等技術對定位節點到錨節點的距離進行測量。RSSI測距技術主要是是利用無線信號強度衰減率與距離的關系進行測距[5],因傳感器節點本身具有通信能力,所以無需增加任何額外的硬件設備,故基于RSSI測距的定位算法是最為簡單、成本低廉的,成為目前研究的熱點。

本文提出了一種基于環境自適應RSSI測距模型的混合型定位算法,精度高于WELSE及WCLA定位算法。

1 測距模型及特性分析

對于RSSI測距,尋找準確的RSSI-距離關系模型對于定位的精度是關鍵。常見的RSSI-距離模型有自由空間傳播、兩徑反射、Shadowing、哈它等。在實際中更具綜合性的Shadowing經驗模型[6]得到了更為廣泛的應用(見圖1)。Shadowing模型由式(1)給出:

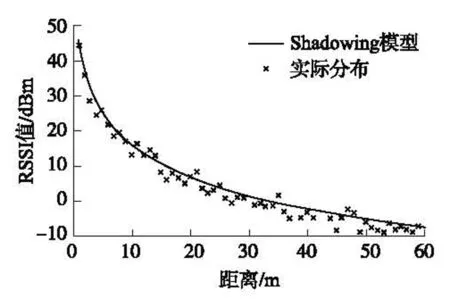
圖1 Shadowing模型

PL(d)=PL(d0)-10nlg(d/d0)+Xσ

(1)

式(1)中,d為接收端到信源的距離,d0為參考距離,PL(d)為接收信號強度(dBm),PL(d0)為在參考距離處的信號強度,n為傳播系數,反映信號隨距離的衰減速率,Xσ為均值為零的信道白噪聲,在上述模型中PL(d0)和n參數都要通過實地測量確定。在應用中通常取參考距離d0為1m處的信號強度值PL(1),此值記為常數A[7],所以式(1)可變換為如下形式:

PL(d)=A-10nlgd+Xσ

(2)

相關研究表明,信號強度與距離存在對應關系,信道噪聲是構成模型不確定性的主要來源。Shadowing模型在實際應用中主要存在如下問題導致其環境適應性較差:①Shadowing模型參數不能自整定,需要在定位區域進行預測量以獲取PL(d0)和n參數;②Shadowing模型雖然考慮到了環境影響因素,但是由于在定位范圍不同區域的多徑反射、溫濕度等衰減特性不盡相同,難以滿足實際多變的環境特性而帶來較大的模型誤差。

由于多徑反射、溫濕度等帶來的傳播系數變化在室內、礦井等環境內是十分普遍的,難以用濾波的方式加以消除,如果所有區域使用相同的模型參數,整體上會帶來較大的測距誤差。為了提高測距模型的環境適應性,環境自適應的定位算法的核心在于由不同區域錨節點分別辨識出其適應于本區域的測距模型,辨識過程是在線進行的,因此可以實現定位算法的環境自適應。

2 自適應RSSI測距模型

2.1 自適應測距模型的構建

首先獲取當前錨節點接收到的相鄰錨節點坐標值及信號強度值r,然后建立以r為自變量的待定系數m次多項式,r的函數y(r)代表當前錨節點到相鄰錨節點的距離,得到下面的測距模型(式(3)):

y(r)=α0+α1r+α2r2+…+αmrm

(3)

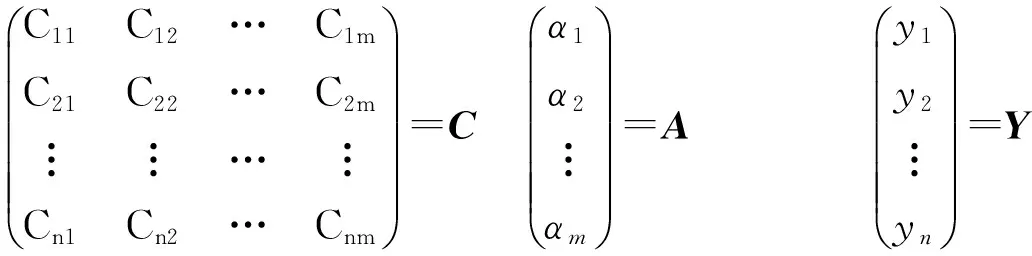
將當前錨節點接收到的n個(n>m)相鄰錨節點信息后代入上式,得到如下方程組:

其中系數α1,α2,…,αm待定,然后使用多項式加權最小二乘擬合,求解出待定系數。

2.2 自適應測距模型的辨識

確定y(r)表達之后,以當前錨節點與鄰錨節點的實際距離y與由測距模型得到的距離y(r)之差的平方和最小為條件來選擇y(r)中的系數。實際距離由坐標關系計算得到:

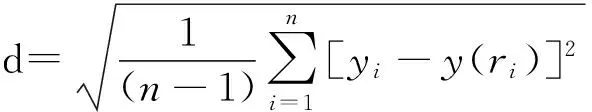
Prcv(d)=Prcv(d0)·(d0/d)λ=C·(1/d)λ

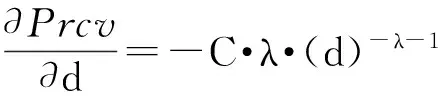
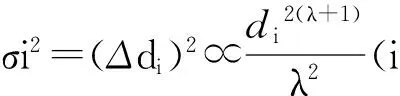
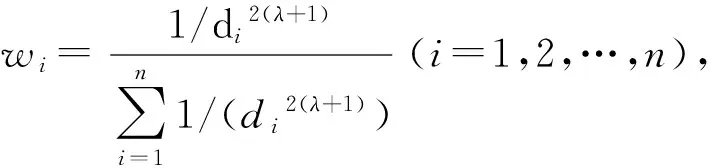
2.3 環境自適應測距模型(SDM)測試

首先通過實測以獲取實際環境中RSSI-距離關系數據。將Tx節點固定,每間隔1 s發射一次信號,Rx節點每間隔1m距離讀取RSSI值。在每個距離測試點Rx連續讀取20組RSSI數據取平均,以濾除隨機干擾影響。通過實測獲得了3種室內環境和3種室外環境在不同溫濕度條件下的多組數據。Tx和Rx節點采用符合IEEE802.15.4/ZigBeeTM規范的的CC2430模塊[12],天線增益10dBi,無線協議棧軟件采用ZStack-1.4.3-1.2.1。

為了研究場地特性對信號傳播特性的影響,在上述實測數據中選取了同種溫濕度條件下的三塊不同的室內場地(IE1-3)數據。為了研究溫濕度條件對信號傳播特性的影響,選取了同一塊場地(EE1)的三組溫濕度數據。從圖2看到,不同的場地對傳輸曲線的中近端(0～12 m)范圍的影響較大,對遠端的影響較小,室內環境影響主要是反射和遮擋等因素。從圖3看,溫度-濕度因素對傳輸曲線也有較大的影響,在高溫、高濕環境下,信號的衰減顯著增大。

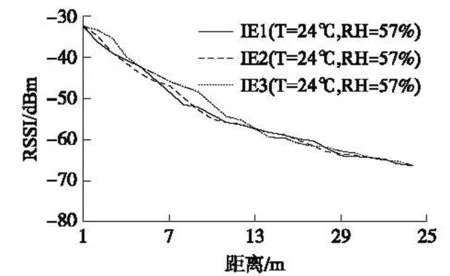
圖2 場地對傳輸特性影響

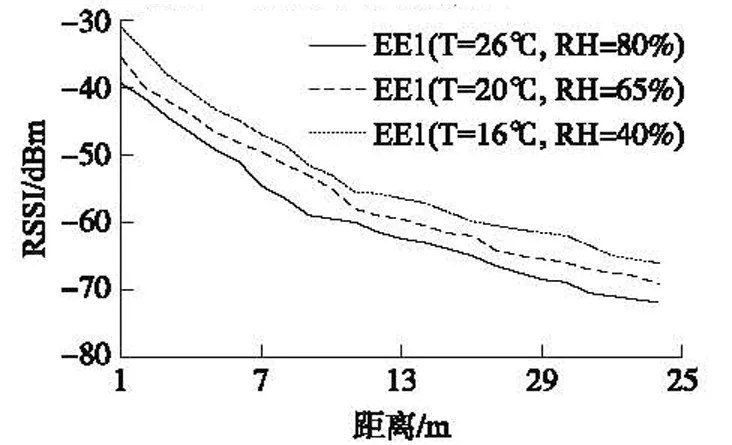
圖3 溫濕度對傳輸特性影響

本文隨機選擇了五組不同環境實測數據(EE1～EE5),來測試測距模型(SDM)效果,使用三次多項擬合,選擇了Shadowing曲線(式(2)確定)作為對照組。式(2)中的A參數通過現場測量得到。為了消除天線方向性影響,將發射節點(Tx)置于原點,將接收節點(Rx)置于半徑為1 m的圓周上(見圖4),正對源節點,每隔45°弧長進行一次測量,每次測量值取20組RSSI值的平均,最后對各次測量求平均得到A參數[13]。經驗曲線的N參數通過與實測數據的擬合得到。5種環境下分別測量以取得各自的A和N參數。Shadowing曲線可由兩種擬合方式得到:通過最小二乘擬合得到曲線LS或通過距離加權最小二乘擬合得到曲線WLS。圖5展示了在第1個測試環境(EE1)下的LS、WLS、SDM擬合效果對比。通過對5種環境(EE1～EE5)的測試(見圖6),LS的平均測距誤差為1.87 m,WLS為1.29 m,SDM為0.12 m。在上述測距算法中,SDM取得了最高的測距精度,而且不需要預整定模型參數,實現了環境自適應。

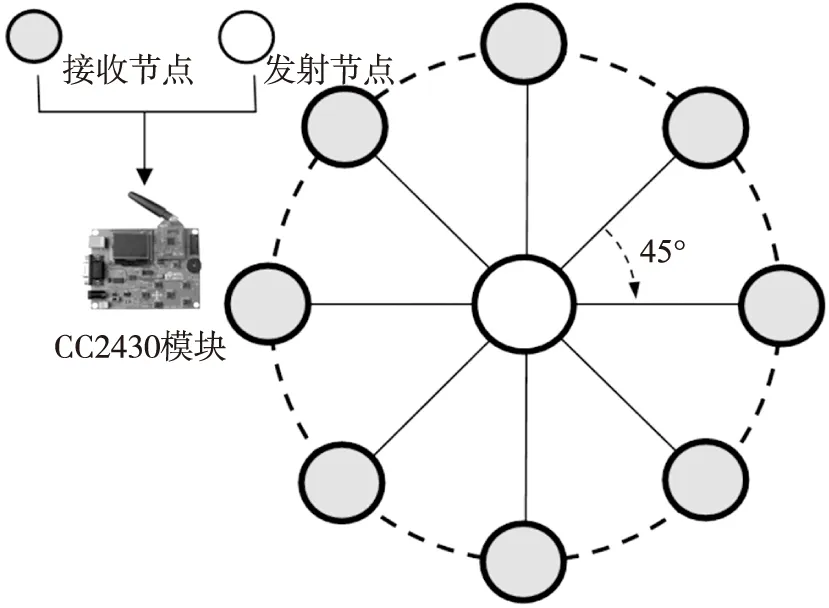
圖4 Shadowing的A參數獲取

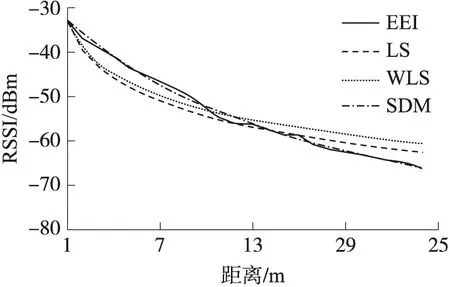
圖5 擬合曲線對比

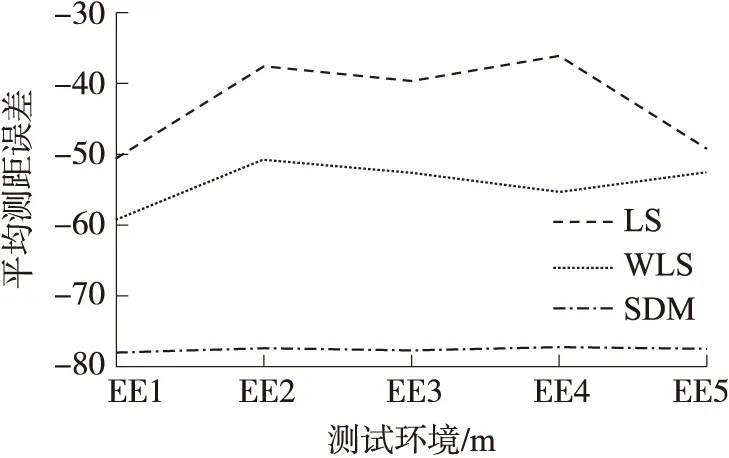
圖6 測量誤差對比

3 改進后的混合自適應定位算法

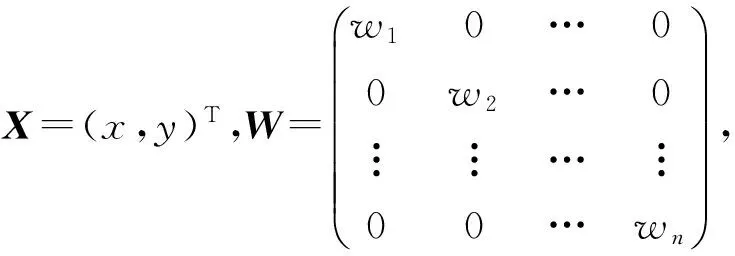
如2.2小節所述,各節點的距離測量誤差是異方差性的,需要引入距離權值進行修正。在WLSE中,距離權值取距離的倒數,不夠準確。在本文的測距模型中,對距離權值進行精確的求解得到權值矩陣W。然后在WLSE上引入修正后的權值矩陣W,獲取定位誤差的無偏估計,得到改進加權極大似然估計定位算法(EWLSE),具體算法如下:

設有n個錨節點Rf1(xb1,yb1)、Rf2(xb1,yb1)、…、Rfm(xb1,yb1)。d1、d1、…、dn分加別為定位節點到各錨節點的距離。根據距離關系有:

解得:X=(ATWA)-1AWB

SDM和EWELSE結合,得到了一種基于自適應測距模型的混合定位算法HSLA(HybridSelf-adaptedLocationingAlgorithm)。為了測試HSLA算法的效果,選取了極大似然估計(LSE)、WELSE和WCLA定位算法作為對比,使用MATLAB進行仿真。為了模擬實際環境的不確定性,所有節點在定位范圍內隨機分布,節點A參數取1m處能量均值-33dBm上下20%范圍(-50.4～-33.6)內隨機值,n參數取一般環境范圍(2～5)內的隨機值。對于LSE、WELSE和WCLA使用經驗算法(式(2)),A參數使用固定均值-33,n參數取環境均值3.5,利用式(2)算法進行測距,HSLA利用自適應測距模型進行測距。仿真結果如圖7和圖8所示。

從圖7可以看到,定位精度隨著錨節點數量的增加而提高,同時最大定位誤差會降低。HSLA的平均定位誤差比WELSE的小49%,比WCLA的小36%。從圖8中可以看,HSLA的最大定位誤差比WLSE小41,比WCLA小22%。WELSE比LSE有著更好的定位精度,顯示出距離權值在提高定位精度中的明顯作用,而HSLA通過自適應測距模型得到的最優距離權值具有更好的效果。整體測試結果表明,HSLA具有在傳播特性非均一的未知環境中具有最高的定位精度。

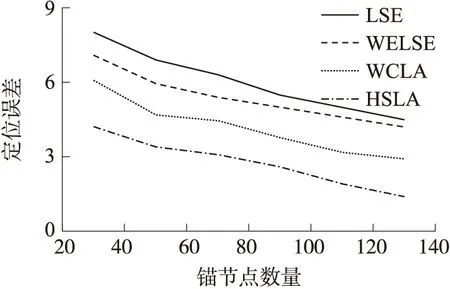
圖7 平均定位誤差

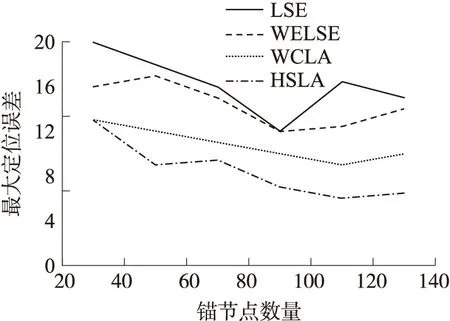
圖8 最大定位誤差

4 結束語

本文針對實際定位環境不確定性因素帶來的測距誤差問題引入了基于環境自適應測距的混合定位方法(HSLA)。使用加權最小二乘法辨識出所在環境的測距模型,這個過程是在線進行的,可以避免經驗模型中預整定參數導致的環境誤差。在HSLA中為了降低測距噪聲帶來的定位誤差,研究了噪聲的特性、與測距距離的關系,根據無偏估計原則構造出改進WELSE中的距離權值。測距實驗表明該算法對不同環境具有自適應性,并達到了較高的精度。計算機仿真證明本文定位算法具有良好的環境適應性和較高的精度。從實驗結果看,該定位算法符合一般性應用場合,具備普遍意義。

[1]陳錫劍,程良倫.基于RSSI的功率匹配定位算法的研究與實現[J].傳感技術學報,2013,26(5):709-714.

[2]王新芳,張冰,馮友兵.基于粒子群優化的改進加權質心定位算法[J].計算機工程,2012,38(1):90-95.

[3]徐原博,鐘麗鴻,崔洋,等.基于無線傳感器網絡的極大似然定位法的分析[J].傳感器與微系統,2011,30(10):37-43.

[4]Girod L,Estrin D.Robust Range Estimation Using Acoustic and Multimodal Sensing[C]//IEEE,eds.Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS01).Maui,USA:IEEE,2001:1312-1320.

[5]方震,趙湛,郭鵬,等.基于RSSI測距分析[J].傳感技術學報,2007,20(11):2526-2530.

[6]朱明輝,張會清.基于RSSI的室內無線網絡定位技術研究[J].現代電子技術,2010(17):45-48.

[7]張嬌.基于接收信號強度的定位算法的研究[D].沈陽:東北大學信息科學與工程學院,2010.

[8]陳良澤.用矩陣運算實現曲線擬合中的最小二乘法[J].傳感技術,2001,20(2):30-34.

[9]高國勝,陳俊杰,李剛.基于RSSI測距的信標節點自校正定位算法[J].測控技術,2010,28(8):93-97.

[10]何曉群,劉文卿.淺談加權最小二乘法及其殘差圖[J].統計研究,2006(4):53-57.

[11]Rappaport T S.Wireless Communication Principles and Practice.Upper Saddle River:Prentice Hall PTR,1996:70-74.

[12]TI/Chipcon.CC2430 Prelimin Data Sheet(rev.2.1)SWRS036F[DB/OL].http://www.ti.com/lit/ds/symlink/cc2430.pdf,2007-05-30.

[13]章堅武,張璐,應瑛.基于ZigBee的RSSI測距研究[J].傳感技術學報,2009,22(2):285-288.

A Positioning Method of WSN Based on Self-Adapted RSSI Distance Model*

YANGWenbo,XINGPengkang,LIUYanhua*

(Electroincs Department,Henan Polytechnic Institute,Nanyang Henan 473000,China)

In order to improve the adaptability and precision of wireless positioning technology of the nodes in WSN,we first analyzed the effects of environmental factors and channel noises on the characteristics of signal transmission and then get the accurate RSSI distance measurement model of environment adaptive.On the base of the distance model and improved WELSE alghorithm with distance weighted correction,we get a new hybrid positioning algorithm of WSN.The tests on the CC2430 platform show that in unknown environments there is no need to calibrate algorithm parameters in advance and the accuracy of positioning is increased by 49% compared to WELSE and by 36% compared to WCLA.The results prove that,the algorithm is well environment adaptive with high precision.

WSN;node positioning;RSSI distance measurement;environment adaptive;WELSE

楊文鉑(1981-),男,漢族,河南南陽人,工學碩士,河南工業職業技術學院電子工程系講師,主要研究方向為無線傳感器網絡和嵌入式系統,wenbostd@126.com;

邢鵬康(1984-),男,漢族,陜西西安人,工學碩士,河南工業職業技術學院電子工程系講師,主要研究方向為物聯網技術及應用;

劉彥華(1977-),女,漢族,河南新鄉人,河南工業職業技術學院電子工程系副教授,工程碩士,主要研究方向為智能控制技術,lyhqxi@163.com。

項目來源:河南省科技攻關項目(142102310225)

2014-08-21 修改日期:2014-11-12

C:5210C;7310N

10.3969/j.issn.1004-1699.2015.01.024

TN98

A

1004-1699(2015)01-0137-05