一種EKF-WLS-SVR與混沌時間序列分析的瓦斯動態預測新方法*

付 華,訾 海,孟祥云,孫 璐

(1.遼寧工程技術大學電氣與控制工程學院,遼寧 葫蘆島 125105;2.國網遼寧省電力有限公司錦州供電公司,遼寧 錦州 121000)

?

一種EKF-WLS-SVR與混沌時間序列分析的瓦斯動態預測新方法*

付 華1*,訾 海1,孟祥云2,孫 璐1

(1.遼寧工程技術大學電氣與控制工程學院,遼寧 葫蘆島 125105;2.國網遼寧省電力有限公司錦州供電公司,遼寧 錦州 121000)

針對瓦斯濃度時間序列高度的混沌特性,采用微熵率法同步確定最優的嵌入維數與延遲時間,還原瓦斯涌出系統狀態空間。以無線傳感網絡系統采集并經降噪處理后的瓦斯濃度序列作為樣本。提出利用帶有整定因子的擴展卡爾曼濾波器(EKF)對加權最小二乘支持向量回歸機(WLS-SVR)的正則化參數γ與核參數σ進行快速尋優,并依據周期性更新的訓練樣本建立基于EKF-WLS-SVR耦合算法的動態預測模型以精確預測后續時間點的瓦斯濃度。通過MATLAB進行仿真,結果表明:EKF濾波器對提高WLS-SVR的擬合精度與學習效率方面有很大的幫助。相比于其他模型,該耦合模型具備更高的預測精度與更強的魯棒特性,有較高的實用價值。

動態預測;瓦斯濃度;混沌特性;無線傳感網絡;WLS-SVR;EKF濾波器

對回采工作面瓦斯濃度進行實時監測和準確預測是防治瓦斯突出災害的關鍵也是煤礦安全生產的前提。以無線傳感網絡技術、數據庫技術以及數據采集技術為一體的瓦斯監測系統是目前主流的綜合信息處理平臺。通過移動節點全覆蓋井下的監測區域,能夠實現對瓦斯濃度的實時監測[1]。在預測算法方面,國內外許多學者提出了支持向量機[2]、人工神經網絡[3]、小波分析[4]、灰色理論[5]、D-S理論[6]等基于機器學習的預測方法。這些方法都是對瓦斯濃度短期預測的有益探索。然而,由于回采工作面地質條件的復雜性。開采期間的瓦斯涌出影響因素會發生一定程度的突變或漂移,致使井下現場采集的瓦斯濃度時間序列表現為較強的非平穩性、非線性和非高斯特性[7]。若采用單一的預測算法或固定的訓練樣本,預測模型的時效性不長,泛化能力上也有一定的缺陷,實用性不高。為此,本文進一步針對提高瓦斯濃度連續預測的精度及可靠性方面展開了研究。

基于結構風險最小化的加權最小二乘支持向量回歸機(WLS-SVR)非常適合小樣本學習且擬合精度較高[8-9]。將WLS-SVR需要優化的正則化參數γ與核參數σ作為擴展Kalman濾波器(EKF)的狀態向量進而對其進行最優估計以得到全局最優參數。為加強耦合算法對瓦斯濃度混沌時間序列預測的可靠性,提出了周期更新訓練樣本的在線動態預測方式。通過微熵率法同步求取最優嵌入維數m與延遲時間τ以還原系統狀態空間,并在重構的相空間里建立基于EKF-WLS-SVR耦合算法的預測模型來實現對回采工作面瓦斯濃度的精準預測。

1 基于無線傳感網絡的瓦斯監測系統

無線傳感網絡瓦斯監測系統由移動傳感器節點、固定傳感器節點以及井上信息處理中心3部分組成。其中,井下大量的移動節點依據通信空間關系或地理位置分為若干個簇并且以自組網的方式將感知的現場數據信息匯聚到簇首[10]。簇首以一個固定節點作為路由將信息通過光纖實時傳輸到井上信息處理中心的網關服務器。井上監控計算機處理信息后,實時顯示出瓦斯濃度及井下相關數據。

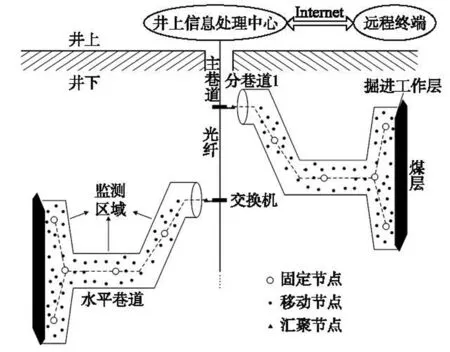
圖1 無線傳感網絡瓦斯監測系統架構

目前國內的瓦斯監測系統依然為落后的事后預警方式,即僅當瓦斯積聚超限時才報警,不具備對瓦斯濃度趨勢演化的提前預測功能。因此,根據無線傳感網絡瓦斯監測系統采集到的信息數據,提出在井上監控計算機上建立基于EKF-WLS-SVR的瓦斯動態預測模型,以實現一種可靠、精確且具備連續非接觸式預測能力的瓦斯災害預警新方法。

2 瓦斯濃度混沌時間序列分析

由Takens定理可知,在選取合適的嵌入維數m和時間延遲τ的情況下,對一維瓦斯濃度混沌時間序列進行相空間重構就可以在更高維的空間里,通過非線性回歸預測函數無奇異地擬合瓦斯涌出動力系統的演化軌跡[11-12]。

2.1 選取最優嵌入維數m與延遲時間τ

以N個樣本數據與其Ns個替代數據之間的相空間微熵率最小為測度,同步考慮確定最優的嵌入維數m與延遲時間τ。避免了兩個參數分開確定時造成算法上的矛盾。

(1)

ρj是第j個延遲矢量與最近鄰點之間的歐氏距離;CE≈0.577 2為歐拉常數。則數據序列熵率為:

(2)

其中,n為延遲矢量個數n=N-(m-1)τ;〈·〉i是Ns個替代數據的微熵H(xs,i)的平均值算子。

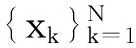
Xi=[xi-(m-1)τ,xi-(m-2)τ,…,xi]T,i=(m-1)τ+1,…,N

(3)

2.2 在線更新訓練樣本的動態預測策略

提出“滑動窗口”的思想,初始窗口數據序列{xj,…,xj+N-1}的長度為N。預測模型f僅以當前窗口數據序列按式(3)重構后的訓練樣本所建立并且僅預測當前窗口之后的W個數據點。預測完成后,窗口向前滑動W個數據點并再次建立新的預測模型f′。即模型的更新周期為W。預測模型在線更新流程如下:

①將模型f有效期間預測的W個預測點替換原窗口數據序列中前W個數據點,則滑動后的窗口數據序列為{xj+W,…,xj+W+N-1}且窗口長度保持為N;

②再次根據微熵率法確定更新后的窗口數據序列的最佳嵌入維數m′與延遲時間τ′。將重構出的N-(m′-1)τ′-1個相點作為預測模型f′的訓練樣本:

{?Xj+W+(m′-1)τ′,xj+W+1+(m′-1)τ′」,…,?Xj+W+N-2,xj+W+N-1」}

③利用新的訓練樣本確立模型f′并再次預測出后續W個數據點,窗口向前滑動。循環以上過程直至指定的預測步數。

更新后的窗口數據序列在時間上距離待測點更近。同時,對其以最優的嵌入維數與延遲時間重構出的訓練樣本能夠保證模型與待測點間存在最大相關性。即動態更新的樣本為預測模型提供了與當前瓦斯涌出非線性動力系統相匹配的先驗知識。

3 WLS-SVR回歸算法

WLS-SVR算法,繼承了LS-SVR求解的快速性并且根據訓練誤差對訓練樣本分配權重系數vi以增強了預測函數對異常點的抗干擾能力。解決了LS-SVR魯棒性缺失的問題。綜合考慮,采用WLS-SVR算法來擬合映射函數f:Rm→R以建立預測模型。

定義樣本集為{(xi,yi)|i=1,2,…,N}。WLS-SVR函數逼近問題可以歸納為如下優化問題:

其中:γ為正則化參數,ω為權矢量,δi為誤差變量,b為偏差量。構造拉格朗日方程:

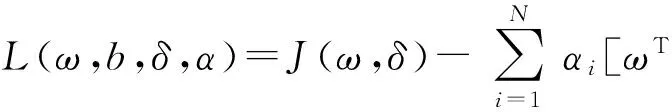
對上式各變量求偏導并消去ω,δi。可得:

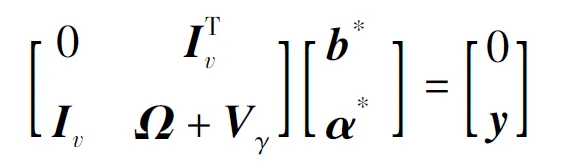
(4)

vi依據于標準LS-SVR誤差變量δi=αi/γ選取

根據實際工程經驗選取徑向基核函數K(xi,xj)=exp(-‖xi-xj‖2/2σ2)。由式(4)求解α*與b*,確定映射函數:

(5)

4 EKF-WLS-SVR動態預測模型

正則化參數γ與核參數σ的選取直接影響WLS-SVR的預測精度。因此,需要對這兩個參數進行全局尋優。常用的K折交叉驗證法需要對訓練樣本進行反復的計算驗證,耗時極大。PSO等群優化算法過度依賴初始粒子的設置,后期收斂速度慢、容易陷入局部極值。這些方法均不適合應用于預測模型的在線學習。

為此,提出將基于Kalman濾波迭代的最優估計思想引入到WLS-SVR的參數尋優上。將WLS-SVR的訓練過程等效成一個非線性離散系統的動態參數估計問題。即以最小無偏差為準則,隨觀測序列不斷對狀態向量進行重估。對于非線性系統要用到擴展Kalman濾波算法(EKF)[13-14]。

4.1 引入整定因子ξ改進EKF算法

對于一般非線性離散系統

(6)

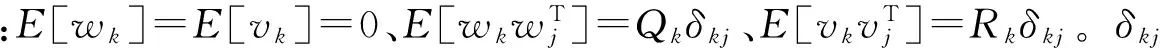
則EKF濾波器的最優估計迭代方程為:

(7)

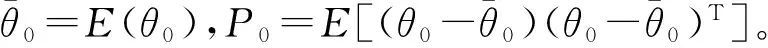
在模型的訓練過程中,混沌的瓦斯濃度序列會導致觀測噪聲具有未知的統計特性。為快速準確跟蹤樣本序列的隨機變化,引入一個整定因子ξ對誤差方差陣進行自適應地調整。使EKF算法能夠快速迭代出滿足精度的最優參數。定義整定因子:

ξk=sup(1,tr[Nk-1]/tr[Mk-1])

(8)

ρ為遺忘因子且0<ρ≤1,一般取ρ=0.97。

4.2 EKF優化WLS-SVR

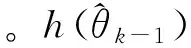
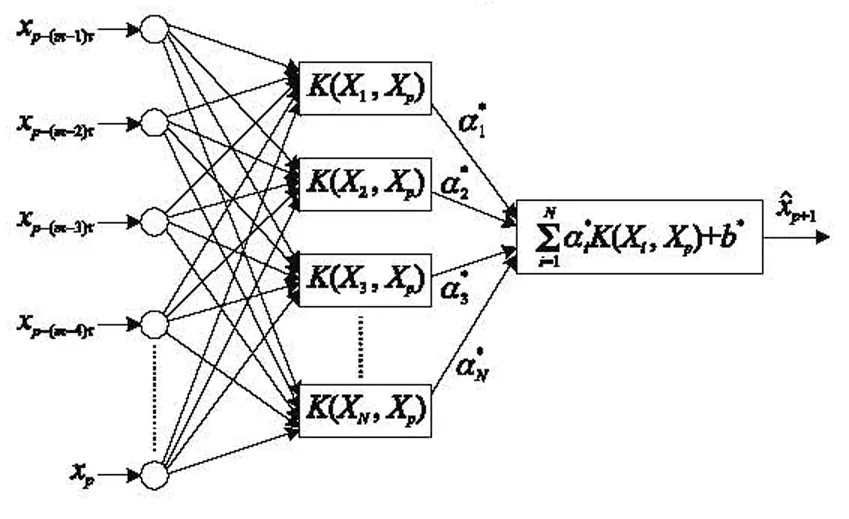
圖2 基于WLS-SVR的單步預測

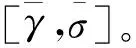
引入整定因子ξ后濾波迭代過程變為:

(9)

當樣本觀測值中有突變點時,殘差ek會增大并直接導致殘差方差陣rk的增大,由式(8)可知整定因子ξk也會相應增大。根據式(9)迭代過程,最終濾波增益Kk相應變大。因此,通過整定因子ξ使得每次迭代時為響應外界噪聲的突變所產生的自適應調整作用最終落實到了對狀態向量的修正上,同時避免了濾波發散。所以,改進后的EKF更適合在線訓練以瓦斯混沌時間序列重構為訓練樣本的WLS-SVR預測模型。

EKF濾波器優化WLS-SVR步驟:

Step 1 對狀態向量的誤差協方差陣P0、系統噪聲的方差陣Q、觀測噪聲方差陣R進行初始化設定;

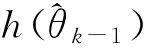
Step 3 通過式(9)迭代方程計算當下的誤差方差陣P與濾波增益K并修正由WLS-SVR的參數γ與σ組成的狀態向量。

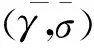
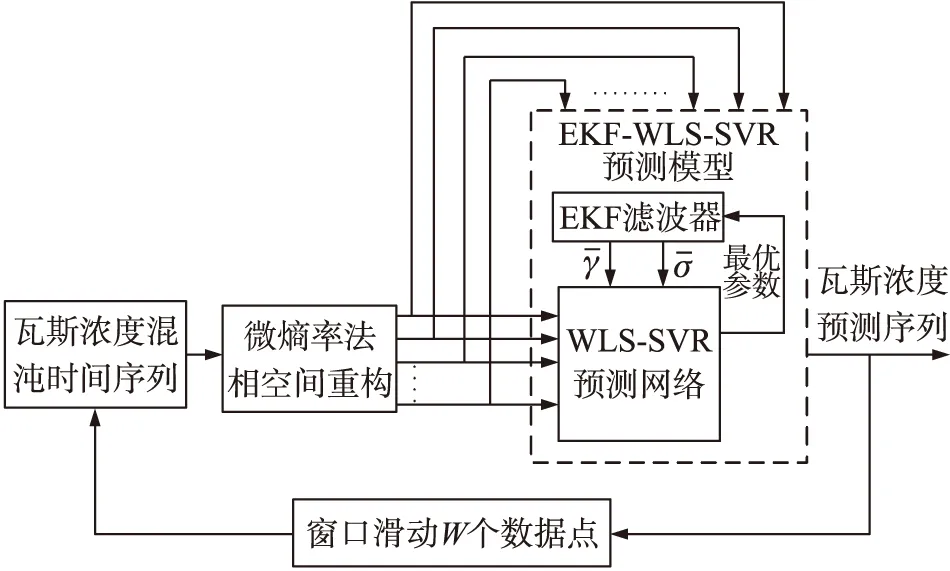
圖3 EKF-WLS-SVR動態預測示意圖

5 瓦斯濃度預測試驗

5.1 數據預處理

試驗數據來自開灤礦業集團錢營礦2074綜采工作面的KJ90N煤礦安全綜合監測系統。截取2013年12月份中的300個未發生瓦斯突出的瓦斯濃度實測數據和另外300個發生瓦斯突出異常時的瓦斯濃度實測數據作為研究對象。

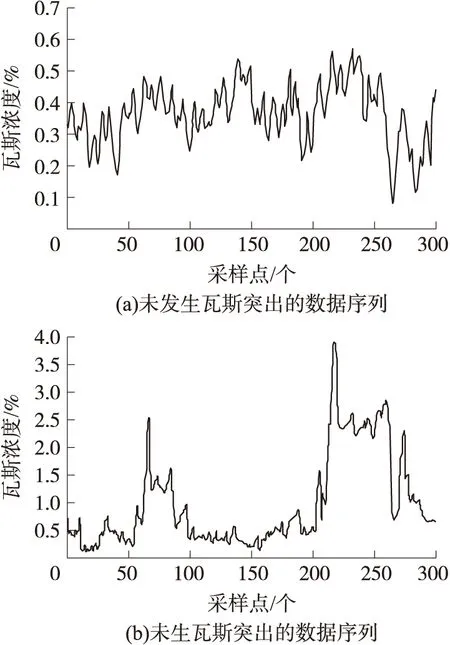
圖4 去噪后的瓦斯濃度觀測序列

采用sym8小波基函數對觀測序列進行軟閾值濾波降噪并利用文獻[15]的方法計算兩組數據序列的最大Lyapunov指數:λ1=0.024 795、λ2=0.085 316。均大于零,說明兩組瓦斯濃度序列均具有混沌特性且λ2>λ1表明發生瓦斯突出異常時,數據序列(b)表現出的混沌行為更加明顯。

5.2 預測過程

時間窗初始化,即將260個觀測數據裝載到時間窗口。試驗選取訓練樣本更新周期W=20,模型f1預測前20個待測點。時間窗口滑動后建立模型f2并預測后20個待測點。利用式(2)對初始窗口數據序列求取微熵率并構出熵率圖如圖5所示。

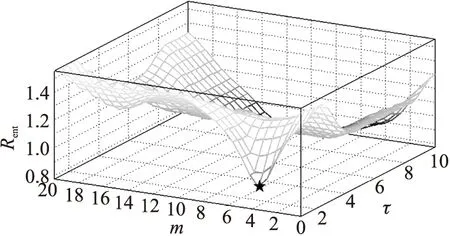
圖5 瓦斯混沌時間序列熵率圖

根據圖5初始窗口序列的微熵率最低點“★”分別對應的m軸與τ軸的值求出m1=6,τ1=3。通過重構相空間可得到244組訓練樣本建立模型f1。初始化EKF濾波器參數:ρ=0.94,β=1.6,P0=50I,Q=40I,R=40I(I為2×2的單位陣);規定模型訓練的允許誤差范圍為10-4以下。

EKF-WLS-SVR的訓練收斂效果如圖6所示,EKF濾波器優化WLS-SVR時迭代到350次左右便達到了訓練誤差精度要求,相比PSO算法尋優更快速并且收斂精度也提高了接近2個數量級。明顯提高了WLS-SVR的學習效率。

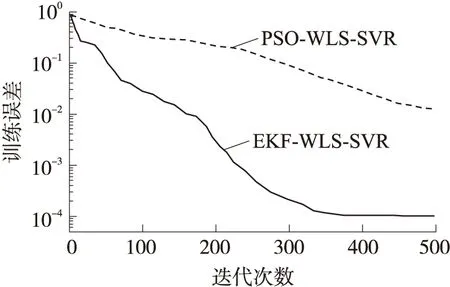
圖6 EKF與PSO的收斂性對比

5.3 試驗結果分析

通過MATLAB2009a進行預測算法仿真,對數據序列(a)的40個待測點的預測結果如下:

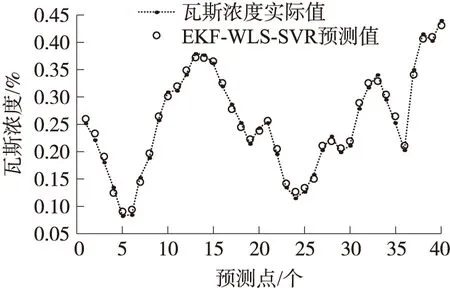
圖7 數據序列(a)的瓦斯濃度預測值與實際值對比

可以看出在未發生瓦斯突出時,基于動態訓練樣本的EKF-WLS-SVR預測模型對于變化趨勢平緩且均勻的瓦斯濃度混沌序列具有較高的預測精度和泛化能力。最大相對誤差為2.17%,最小相對誤差僅為0.41%,平均相對誤差為1.05%。滿足煤礦實際安全生產的精度需求。

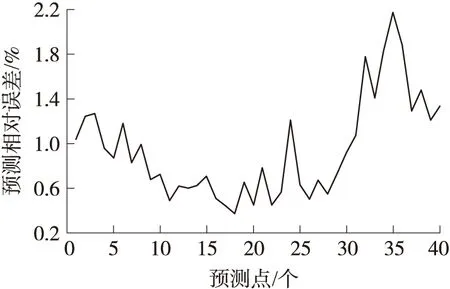
圖8 預測結果相對誤差

發生瓦斯突出時,從數據序列(b)中可以看出此時的瓦斯濃度激增,變化幅度異常且含有較大的未知噪聲。分別利用EKF-WLS-SVR與LS-SVR對序列(b)后續40點進行預測。以對比突出耦合模型對數據異常時的預測魯棒性和可靠性。

預測結果如圖9所示,EKF-WLS-SVR對于瓦斯突出時的預測平均相對誤差為4.72%,依然滿足實際精度要求,而LS-SVR卻為15.78%。表明WLS-SVR根據訓練誤差以建模貢獻度對樣本采取的加權策略從本質上提高了模型對異常數據的魯棒性。使得耦合算法依然能夠準確跟蹤大幅度隨機突變情況下瓦斯濃度序列的變化規律,預測效果明顯強于LS-SVR。同時引入了整定因子ξ的EKF濾波器能夠在線及時獲得最優參數,保證了模型的預測精度。

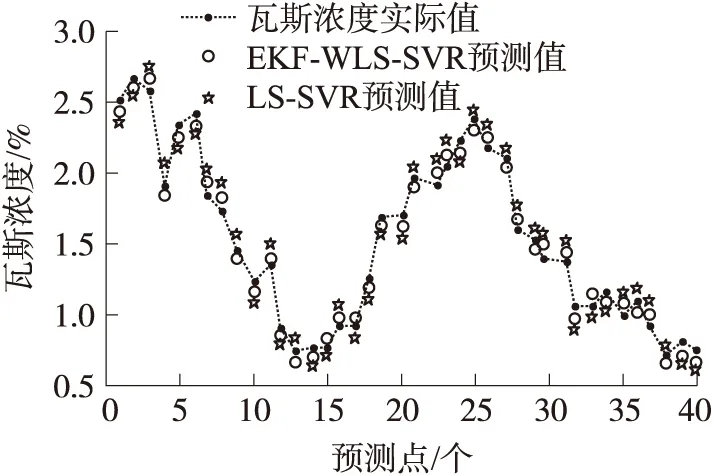
圖9 數據序列(b)的瓦斯濃度預測值與實際值對比

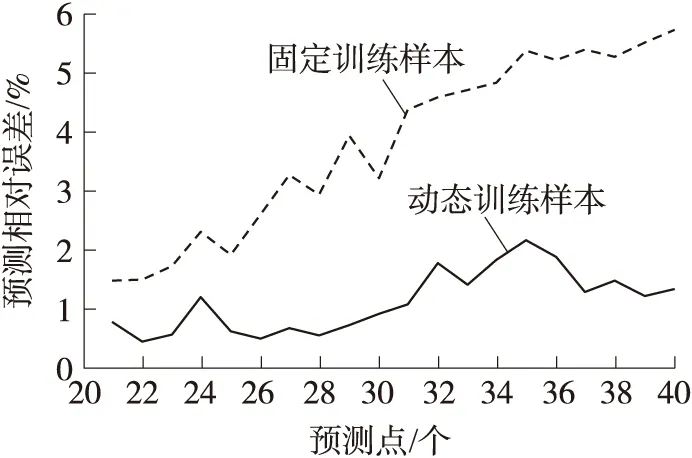
圖10 動態樣本與固定樣本相對誤差對比

為了突出動態樣本的優越性,針對數據序列(a)以f1預測后20個待測點來模擬固定樣本的預測模式。f1與f2對后20個待測點的預測相對誤差如圖10所示。

基于固定訓練樣本的f1在預測過程的后半段預測精度產生了明顯的偏差,最大相對誤差達到了5.73%,說明固定樣本的模型時效性有限。在混沌時間序列初值敏感性的影響下,固定樣本使得WLS-SVR回歸算法無法精確擬合與較遠待測點之間的映射關系。以相對均方根誤差RRMSE為評判標準來評估設置不同更新周期W時模型的預測效果。其表達式為:

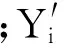
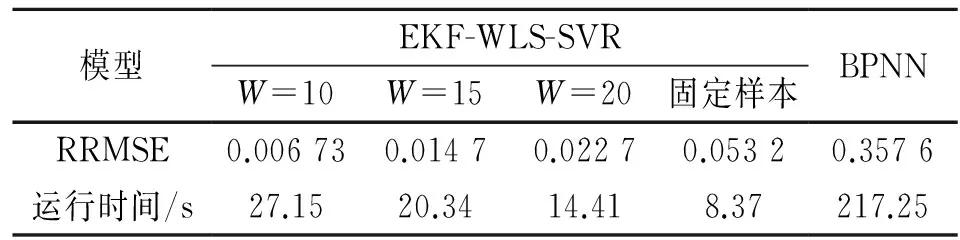
表1 預測效果對比分析

RRMSE結果顯示基于動態更新訓練樣本的EKF-WLS-SVR預測模型的預測平均精度明顯高于基于固定樣本的BP神經網絡預測模型。W取值越小,WLS-SVR的支持向量更新越頻繁且預測模型越能表征當下的瓦斯涌出規律,使其具備更強的在線自適應能力。在運行時間方面,與EKF相結合的WLS-SVR建模所需時間短,學習效率明顯提高。綜合考慮預測精度要求與運行時間,該耦合模型能夠實現混沌時間序列的連續精確預測。對井下瓦斯濃度的實時監測預警具有重大的實際指導意義。

6 結論

本文將基于Kalman濾波狀態空間最優估計思想的EKF濾波器與WLS-SVR回歸算法有機結合起來,有效提高了WLS-SVR的預測精度與學習效率。同時,提出了在線更新訓練樣本的動態預測策略,使得EKF-WLS-SVR耦合模型能夠充分獲得與當下瓦斯涌出動力系統相匹配的先驗知識。保證了預測模型的時效性。利用EKF-WLS-SVR耦合算法建立的動態預測模型對井下瓦斯濃度進行試驗,結果表明:該模型具有較強的魯棒性且預測精度明顯強于其他方法。能夠可靠地對井下回采工作面瓦斯濃度趨勢演化進行提前的精確預測。

[1]王軍號,孟祥瑞.基于物聯網感知的煤礦安全監測數據級融合研究[J].煤炭學報,2012,37(8):1401-1407.

[2]劉俊娥,楊曉帆,郭章林.基于FIG-SVM的煤礦瓦斯濃度預測[J].中國安全科學學報,2013,23(2):80-84.

[3]王其軍,程久龍.基于免疫神經網絡模型的瓦斯濃度智能預測[J].煤炭學報,2008,33(6):665-669.

[4]王曉路,劉健,盧建軍.基于小波變換和優化預測器的瓦斯濃度預測[J].應用基礎與工程科學學報,2011,19(3):499-508.

[5]董丁穩,李樹剛,常心坦,等.瓦斯濃度區間預測的灰色聚類與高斯過程模型[J].中國安全科學學報,2011,21(5):40-45.

[6]邵良杉,付貴祥.基于數據融合理論的煤礦瓦斯動態預測技術[J].煤炭學報,2008,33(5):551-555.

[7]單亞鋒,侯福營,付華,等.基于改進極端學習機的混沌時間序列瓦斯涌出量預測[J].中國安全科學學報,2012,22(12):58-63.

[8]Rubio G,Pomares H,Rojas I,et al.A Heuristic Method for Parameter Selection in LS-SVM:Application to Time Series Prediction[J].International Journal of Forecasting,2011,27(3):725-739.

[9]Hwang J P,Park S,Kim E.A New Weighted Approach to Imbalanced Data Classification Problem Via Support Vector Machine with Quadratic Cost Function[J].Expert Systems with Applications,2011,38(7):8580-8585.

[10]李紀榕,李福進,吳艷微,等.基于無線傳感網絡的煤礦安全監測系統設計[J].傳感技術學報,2011,24(9):1336-1340.

[11]Samanta B.Prediction of Chaotic Time Series Using Computational Intelligence[J].Expert Systems with Applications,2011,38(9):11406-11411.

[12]Song J,Meng D,Wang Y.Analysis of Chaotic Behavior Based on Phase Space Reconstruction Methods[C]//Computational Intelligence and Design(ISCID),2013 Sixth International Symposium on.IEEE,2013,2:414-417.

[13]Frogerais P,Bellanger J,Senhadji L.Various Ways to Compute the Continuous-Discrete Extended Kalman Filter[J].Automatic Control,IEEE Transactions on,2012,57(4):1000-1004.

[14]徐耀松,李一博,付銅玲,等.有限空間液態場中基于優化EKF的雙曲面水聲定位方法研究[J].傳感技術學報,2011,24(11):1579-1583.

[15]張文超,譚思超,高璞珍.基于Lyapunov指數的搖擺條件下自然循環流動不穩定性混沌預測[J].物理學報,2013,62(6):61-68.

A New Method of Mine Gas Dynamic Prediction Based on EKF-WLS-SVR and Chaotic Time Series Analysis*

FUHua1*,ZIHai1,MENGXiangyun2,SUNLu1

(1.Faculty of Electrical and Control Engineering,Liaoning Technical University,Huludao Liaoning 125105,China;2.Jinzhou Power Supply Company of Liaoning Electrical Power Company of State Grid,Jinzhou Liaoning 121000,China)

Considering highly chaotic characteristic of gas concentration time series,the differential entropy ratio method was adopted to synchronously determine optimal embedded dimension and delay time so as to restore the system state space of gas emission.The samples with noise elimination came from the gas concentration series which was collected by wireless sensor networks.Extended kalman filter algorithm(EKF)with tuning factor was proposed to rapidly optimize the regularization parameterγand the nuclear parameterσof the weighted least squares support vector regression(WLS-SVR).Periodically updated training samples were used to establish the EKF-WLS-SVR coupling algorithm-based dynamic prediction model to accurately predict gas concentration in the future.The simulation of the MATLAB shows that EKF is greatly helpful for improving WLS-SVR fitting precision and learning efficiency.The coupling model is practically useful and outperforms other prediction models in terms of prediction accuracy and robustness.

dynamic prediction;gas concentration;chaotic characteristic;wireless sensor networks;WLS-SVR;EKF

付 華(1962-),女,遼寧阜新人,教授,博士生導師,博士(后),主要研究方向為煤礦瓦斯檢測、智能檢測和數據融合技術。支持國家自然科學基金2項、支持及參與國家863和省部級項目30余項,發表學術論文40余篇,申請專利24項,fxfuhua@163.com;

訾 海(1989-),男,遼寧阜新人,遼寧工程技術大學電氣與控制工程學院碩士研究生,主要研究方向為控制理論與控制工程,lngdzh001@163.com。

項目來源:國家自然科學基金項目(51274118);遼寧省教育廳基金項目(L2012119);遼寧省科技攻關項目(2011229011)

2014-07-08 修改日期:2014-10-09

C:7230

10.3969/j.issn.1004-1699.2015.01.022

TP391;TP212

A

1004-1699(2015)01-0126-06