時間偏移下的多源目標精確定位方法

嚴長虹,金 琳

(1.鹽城工學院信息學院,江蘇 鹽城 22400;2.鹽城工學院經濟與管理學院,江蘇 鹽城 22400)

?

時間偏移下的多源目標精確定位方法

嚴長虹1*,金 琳2

(1.鹽城工學院信息學院,江蘇 鹽城 22400;2.鹽城工學院經濟與管理學院,江蘇 鹽城 22400)

采用到達時間(TOA)測距實現源目標定位的方法比較簡單,因此在無線傳感器網絡定位領域得到了廣泛的應用。將TOA定位模型轉化為線性優化問題,提出了一種存在時間偏移下的多源目標精確定位方法。該方法將定位計算過程分成兩步,包括多源目標位置初始值估計和優化計算過程。兩步計算方法將定位結果用代數解表示,避免了數值計算過程中的局部最優問題。仿真分析了時間偏移量及噪聲大小對定位誤差的影響。結果表明即使存在較大的時間偏移量,優化計算后的定位誤差也能非常接近于克拉美羅(CRLB)下界值。

無線傳感器網絡;定位;到達時間(TOA);多源目標

節點位置坐標的自主估計是無線傳感器網絡中的重要內容[1-2],為了滿足部署大量無線傳感器節點的廉價要求,定位的硬件成本必須較低,因此傳統的GPS定位方法對無線傳感器網絡來說是不適合的。GPS定位方法的局限性激發了一種新的傳感器網絡定位方法,即利用已知位置的信標節點去推算其余未知源目標節點的位置坐標。在這種定位方式下,定位過程可劃分為兩步:借助于一定的方法測量或估計節點間的距離或方向角信息;以節點間的這些信息通過定位算法求出源節點坐標。因此,定位精度不但取決于測量技術的精度,而且也決定于所采用的定位算法。

國內外已經開展了很多無線傳感器網絡定位方法的研究,這些定位方法大多數在定位成本和定位精度間進行權衡選擇[3]。通常測距誤差越小,定位算法獲得的定位精度越高,當然對測距方法的要求也就越高。根據定位過程中是否需要直接測量節點間距離,可以把定位算法分為:基于非測距和測距的定位算法。非測距定位算法無需測量節點的絕對距離或方位,而是利用節點間的鏈路關系估計距離并計算節點位置,定位成本較低,但定位誤差相對較大[4]。為獲取較高的定位精度,一般采用測距定位算法。測距定位算法需要直接測量節點間的絕對距離或方向角,并利用節點間的實際距離來計算未知節點的位置,該方法需要測量節點間間距,常用的測量有接收信號強度指示(RSSI)[5-6],到達時間(TOA)[7],到達時間差(TDOA)[8]和聲音能量強度[9]等方法。

在已知信號傳播速度的前提下,TOA方法根據信號在兩個目標之間的傳播時間來估計發送者和接收者之間的距離,相比較而言,其實現原理簡單,因此已有大量的文獻介紹使用該方法實現目標定位[10-14]。Chan等[10]提出了基于一種TOA測距方法下的最優線性無偏估計方法,但該方法沒有考慮節點間到達時間偏差。文獻[11]以目標間的發射與反射TOA測距模型,提出了一種精確的被動目標位置線性估計方法,但該方法并未考慮節點間的時間偏移量。為此Wang等[12]對存在時間偏移量下的被動目標位置估計進行了改進,并提出了定位計算方法。也有學者將定位優化模型轉化為凸優化問題,如文獻[13]提出源節點信號發射時間未知下的半正定規劃(SDP)放松定位算法,但該文獻并未考慮多源定位問題。為此文獻[14]介紹采用SDP放松方法將上述TOA定位模型擴展到多源目標定位。SDP定位方法的不依賴于初始解,但計算復雜度較高。

根據節點間的TOA往返時間測距模型并考慮節點間存在傳送時間偏移量,本文將多源目標定位問題轉化為線性估計模型,以兩步線性計算方法精確確定源目標位置坐標,提出了存在時間偏移量下的多源目標精確定位計算方法。本文第1部分首先介紹了多源TOA定位問題描述;第2部分推導了該定位模型下的CRLB下界值;第3部分詳細介紹了所設計的定位計算方法,包括目標位置初始值估計及優化計算過程;第4部分為仿真與分析;最后部分為結論。

1 問題描述

考慮在二維平面上分布著M+N個節點,其中包括N個未知位置坐標的源節點(源節點的坐標值假設為xi=[xiyi]T,i=1,2,…,N)以及M個已知位置坐標的信標節點(其坐標值為xj=[xjyj]T,j=N+1,N+2,…,N+M,信標節點位置坐標可以預先部署GPS或依靠人力測量方式獲取)。信標節點j發送給源節點i信號,源節點i接收到該信號后立刻又轉發回信標節點j,將節點間的信號往返時間記為ti,j,因此有

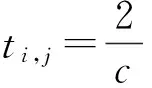
(1)

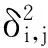
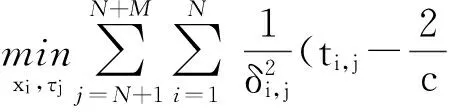
(2)

顯然對式(2)所描述的優化問題可采用數值方法計算。然而當采用數值計算方法時,計算結果依賴于初始值,若初始值選擇不合適,可能會使結果陷入局部最優,導致計算結果錯誤。

為此本文提出一種存在時間偏移下的多源目標位置線性估計方法。該方法采用兩步線性估計方法實現,將定位結果采用代數解表示,避免了數值計算方法下選擇初始解的問題。首先將非線性優化定位模型轉化為線性估計問題,初步估計多源目標節點位置坐標。然后對初步估計的源目標位置進行再次優化求精計算,從而得到目標位置的精確解。

2 克拉美羅下界值

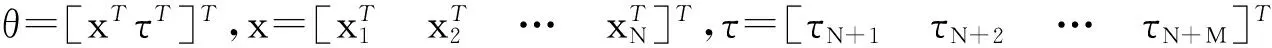
(3)

式(3)中,

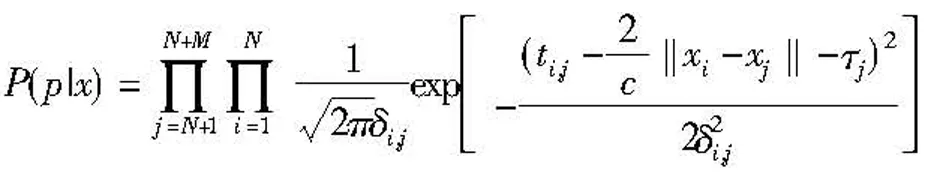
(4)

將式(4)代入式(3)并求微分,因此有F∈R(2N+M)×(2N+M),并且矩陣F的元素值為

(5)

式(5)中,j∈Ai表示了源節點i與信標節點j間可測距。向量θ的CRLB下界為F逆矩陣的對角元素,可以表示為

(6)

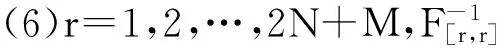
(7)

3 多源目標定位

式(2)所描述的TOA測距模型中包含未知參數τj,故難以實現對單源節點目標位置的確定,本節設計了多源目標的兩步線性估計方法,以精確定位目標節點位置坐標。

3.1 多源目標位置初始值估計

將式(1)重新表示為

2‖xi-xj‖=c(ti,j-τj-ni,j)

(8)

式(8)中,i=1,2,…,N,j=N+1,N+2,…,N+M且j∈Ai。對式(8)左右兩邊平方,忽略高階項,式(8)再表示為

(9)

由于τj?tij,將式(9)再次表示為

(10)

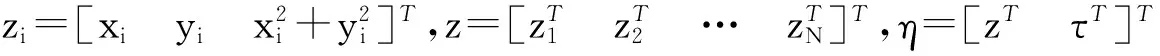
Aη=b+α

(11)

式(11)中,α為噪聲部分,矩陣A的行向量值為:

當所有源節點與信標節點間共存在L次TOA測距時,A∈RL×(3N+M),b∈RL×1,α∈RL×1。

根據線性最小二乘平方原理,未知參數η的無偏估計值為

(12)

式(12)中維度為L×L的矩陣Σα=E(αTα),其值大小為

(13)

式(13)中,Σα的計算取決于參數值τj。可預先設置Σα為單位矩陣,近似地求解時間偏移值τj,j=N+1,N+2,…,N+M,然后以該近似值計算Σα,再以式(12)重新精確計算參數η。

3.2 目標位置優化計算

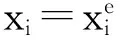
(14)

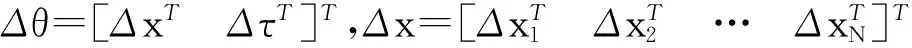
Δτ=[ΔτN+1ΔτN+2…ΔτN+M]T,可將式(14)寫成如下矩陣形式

CΔθ=d+α

(15)

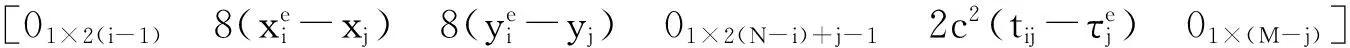
(16)

式(16)中維度為L×L的矩陣Σα=E(αTα),其值計算同式(13)。同樣根據參數Δθ的定義,從參數Δθ抽取出Δxi即為優化增量部分。因此最終的源節點目標位置可以表示為

(17)

式(17)中,i=1,2,…,N。

將參數Δθ的方差表示為ΣΔθ,由式(16)可以推導出ΣΔθ有以下關系式

(18)

3.3 算法的計算復雜度分析

O[2L2(3N+M)+L(3N+M)2+(3N+M)3]≤

O[(3N+M)(2M2N2+3MN2+M2N+(3N+M)2]≈

O(6M2N3+2M3N2)

(19)

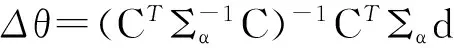
O[2L2(2N+M)+L(2N+M)2+(2N+M)3]≤

O[(2N+M)(2M2N2+2MN2+M2N+(2N+M)2]≈

O(4M2N3+2M3N2)

(20)

4 仿真分析

針對上述所設計的兩步線性估計方法,采用MATLAB軟件進行了仿真與分析。在100m×100m的二維平面上,分別設置5個信標節點(M=5)在(25,25),(25,50),(50,50),(75,25),(75,75)坐標點。同時隨機生成了10個源節點(N=10),當源節點與信標節點間距離小于60m時,認為可實現TOA測距,源節點位置坐標及節點間測距情況如圖1所示。為評價所設計算法的定位性能,源節點的定位精度采用均方誤差(MSE)判斷。假設目標節點與源節點間的測距噪聲都服從均值為0,方差為δ2的高斯分布,首先仿真測試了不同源節點ID上的定位誤差結果。

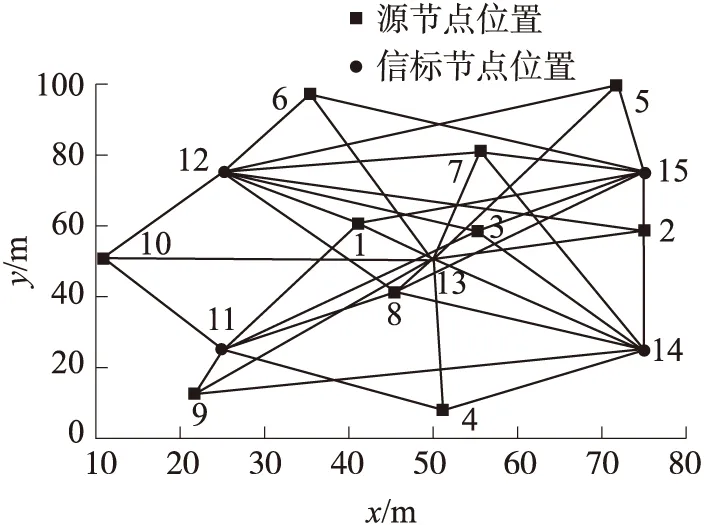
圖1 節點地理位置分布

4.1 不同源節點ID的定位誤差比較

設置所有源節點和信標節點間的測距噪聲為δ2=12,所有信標節點上的時間偏移量τj=τ=20 ns,j=N+1,N+2,…,N+M。對算法下的MSE定位誤差仿真運行5 000次,采用5 000次運行結果的平均值分析其定位誤差,圖2繪出了不同源節點上的定位誤差比較結果。由該圖可見,經過優化計算后,所有源節點上的定位結果較初始估計值有極大的改善,已基本與CRLB下界值一致。由于所采用的信標節點位置分布不同,經過優化計算后各源節點上的定位誤差有所不同,如源節點ID為5的對數MSE值,即10log(MSE)為-11.7 dB,而源節點ID為8的對數MSE值為-15.4 dB。

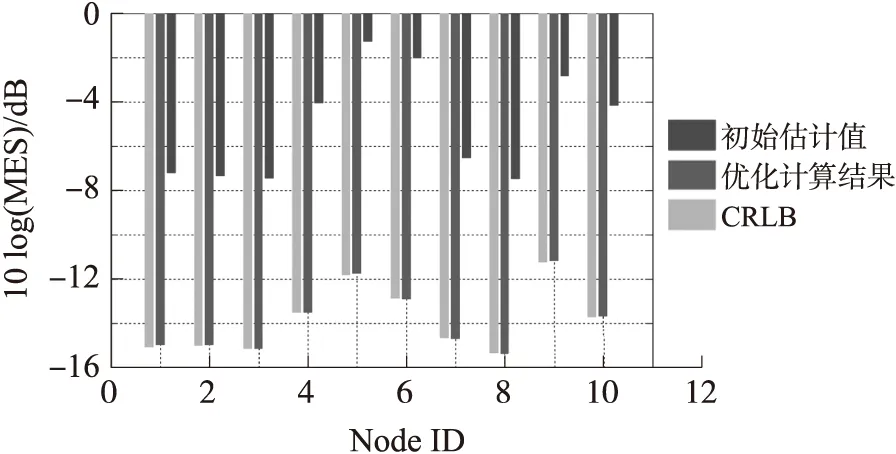
圖2 不同源節點ID的定位誤差比較

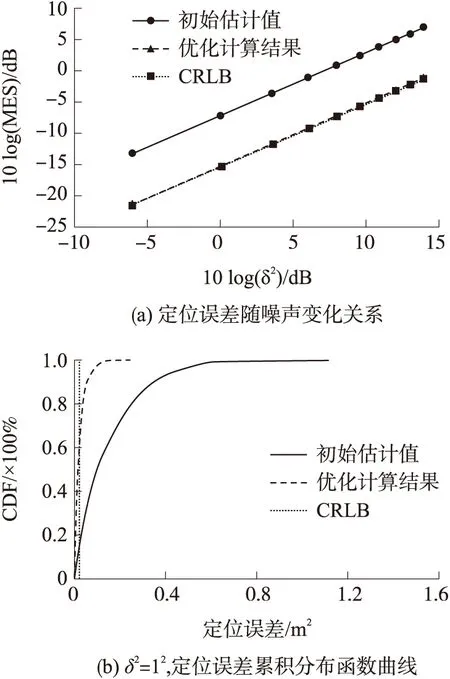
圖3 源節點ID為8時噪聲對定位誤差的影響

4.2 噪聲對定位誤差的影響

調整噪聲δ2從0.52到52之間變化,即10log(δ2)從-6.0dB到14.0dB之間變化,時間偏移量τ=20ns,圖3(a)繪出了源節點ID為8時定位誤差與噪聲之間的變化關系。該圖反映的結果同圖2結果一致,經過優化計算后的源節點定位結果較初始估計值有極大的改善,非常接近CRLB下界值。同時也可以看出對數MSE值與噪聲10log(δ2)之間有近似的線性關系,隨著噪聲的增加而增大。當噪聲10log(δl2)為-6.0dB時,優化計算后的對數MSE值為-21.3dB;而當噪聲10log(δ2)為14.0dB時,優化計算后的對數MSE值增加到了-1.2dB。

設定δ2為12,時間偏移量τ=20ns,圖3(b)繪出了5 000次隨機測試下、源節點ID為8的定位誤差的累積分布函數曲線(CDF)。初始估計值下僅有15%左右的定位誤差小于CRLB,而經過優化計算后,有65%左右的定位誤差小于CRLB下界值,說明經過優化計算后,定位誤差大大減少了。

4.3 時間偏移量對定位誤差的影響

目標位置初始值估計時,方程對時間偏移量進行了近似線性處理,導致初始估計出現偏差,為此仿真分析了時間偏移量τ對定位誤差的影響。設定δ2為12,調整時間偏移量τ從20ns到200ns之間變化,圖4繪出了ID為5和8的源節點的定位誤差隨時間偏移量的變化關系曲線。由該圖可見,初始估計值的定位誤差隨著時間偏移量τ的增加而增大,而經過優化計算后,兩個節點的定位誤差隨時間偏移量τ的增加而保持基本不變。當時間偏移量τ=20ns時,源節點ID為5的初始估計的對數MSE值為-1.1dB,優化計算后的對數MSE為-11.8dB;當時間偏移量τ=200ns時,初始估計的對數MSE值增加到了1.3dB,而優化計算后的對數MSE值仍然為-11.8dB,該結果說明優化計算結果更加可靠。

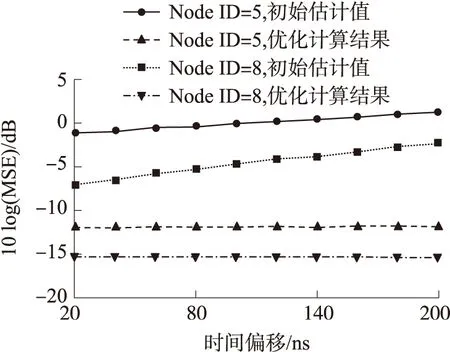
圖4 定位誤差隨時間偏移量的變化關系

5 結論

本文介紹了一種存在時間偏移下的多源目標定位方法。該方法通過目標位置的初始值估計和優化計算兩步過程實現,經過優化計算后的定位精度可以基本和CRLB下界值一致。以多源目標定位問題為出發點,將定位問題模型描述為線性最小二乘估計問題,避免了數值計算方法中因初始值選擇不當而引起的局部最優問題。仿真結果發現,優化計算后的定位結果具有較高的可靠性,在較大的時間偏移量下,其定位誤差還可以保持穩定,非常接近于CRLB下界值。

[1] 葉苗,王宇平.一種新的容忍惡意節點攻擊的無線傳感器網絡安全定位方法[J].計算機學報,2013,36(3):532-544.

[2]Zhao Jizhong,Xi Wei,He Yuan,et al.Localization of Wireless Sensor Networks in the Wild:Pursuit of Ranging Quality[J].IEEE Transactions on Networking,2013,12(1):311-323.

[3]Liu Yunhao,Yang Zheng,Wang Xiaoping,et al.Location,Localization,and Localizability[J].Journal of Computer Science and Technology,2010,25(2):274-297.

[4]Zhong Ziguo,He Tian.Achieving Range-Free Localization Beyond Connectivity[C]//Proceedings of ACM SenSys,2009:281-294.

[5]Robin Wentao Ouyang,Albert Kai-Sun Wong,Chin-Tau Lea.Received Signal Strength-Based Wireless Localization Via Semidefinite Programming:Noncooperative and Cooperative Schemes[J].IEEE Transactions on Vehicular Technology,2010,59(3):1307-1318.

[6]吳曉平,陸炳斌,沈浩.基于RSSI定位模型的非視距關系識別方法[J].傳感技術學報,2013,26(11):1584-1589.

[7]Ismail Güven?,Chong Chiachin.A Survey on TOA Based Wireless Localization and NLOS Mitigation Techniques[J].IEEE Communications Surveys and Tutorials,2009,11(3):107-124.

[8]Yang Le,Ho K C.An Approximately Efficient TDOA Localization Algorithm in Closed-Form for Locating Multiple Disjoint Sources With Erroneous Sensor Positions[J].IEEE Transactions on Signal Processing,2009,57(12):4598-4615.

[9]呂方旭,張金成,劉立陽.基于WSN的多聲源目標定位算法[J].傳感技術學報,2012,25(8):1121-1125.

[10]Chan F K W,So H C,Zheng J,et al.Best Linear Unbiased Estimator Approach for Time-of-Arrival Based Localisation[J].IET Signal Processing,2008,2(2):156-162.

[11]Shen Junyang,Andreas F Molisch,Jussi Salmi.Accurate Passive Location Estimation Using TOA Measurements[J].IEEE Transactions on Wireless Communications,2012,11(6):2182-2192.

[12]Wang Yuan,Ma Shaodan,Philip Chen C L.TOA-Based Passive Localization in Quasi-Synchronous Networks[J].IEEE Communications Letters,2014,18(4):592-595.

[13]Xu Enyang,Ding Zhi,Dasgupta Soura.Source Localization in Wireless Sensor Networks From Signal Time-of-Arrival Measurements[J].IEEE Transactions on Signal Processing,2011,59(6):2887-2897.

[14]Shen Hong,Ding Zhi,Dasgupta Soura,et al.Multiple Source Localization in Wireless Sensor Networks Based on Time of Arrival Measurement[J].IEEE Transactions on Signal Processing,2014,62(8):1938-1949.

Accurate Positioning Approach of Multiple Source Target Under Time Offest

YANChanghong1*,JINLin2

(1.School of information engineering,Yancheng Institute of Technology,Yancheng Jiangsu 224000,China;2.School of Economics and Managment,Yancheng Institute of Technology,Yancheng Jiangsu 224000,China)

It is relatively simple to utilize time of arrival(TOA)ranging for realizing the positioning of multiple source targets,so it is widely applied in the positioning field of wireless sensor networks.Converting the TOA positioning model to the problem of linear optimization,an accurate positioning method for multiple source targets is put forward when there are time offsets.The method divides the process of positioning calculation into two steps,including the initial estimation of multiple source targets and the process of optimization computation.The two-steps calculation method represents the positioning results as the algebraic solutions and avoids the local optimum problem in the process of numerical calculation.The simulations analyze the impacts of time offsets and noises on the positioning errors.The results show that the positioning errors of the optimization calculation can be very close to the Cramer Rao lower bound(CRLB),even if there are larger time offsets.

wireless sensor networks;localization;time of arrival(TOA);multiple source target

嚴長虹(1980-),講師,工學碩士,主要研究方向為無線傳感器網絡、信號分析與處理、網絡安全等。在國內外重要會議及期刊上發表論文十多篇。

2014-10-13 修改日期:2014-11-26

C:6150P;7110

10.3969/j.issn.1004-1699.2015.02.005

TP393.0

A

1004-1699(2015)02-0178-05