Analysis on Factors Influencing Strains of Unbonded Flexible Risers Under Pressures

REN Shao-fei,TANG Wen-yong,XUE Hong-xiang

(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Analysis on Factors Influencing Strains of Unbonded Flexible Risers Under Pressures

REN Shao-fei,TANG Wen-yong,XUE Hong-xiang

(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Abaqus/Explicit quasi-static simulation and mass scaling are adopted to predict strains of a typical unbonded flexible riser under pressures.Factors influencing axial elongation and twist are analyzed.Cross-sectional profiles and lay angles of metallic layers,geometric,contact and material nonlinearities are considered in the numerical model.The computational results show that numerical and analytical solutions are in good agreement;by contrast with elongation,boundary condition has greater impact on twist;pressure armor layer withstands almost all radial pressure;lay angle effect of pressure armor layer,which can be ignored in collapse buckling study,must be considered in strain analysis;lay angle of tensile armor layers also has great influence on strains.The numerical method can remedy defects of analytical approach which limited in small displacements and strains, with friction,material nonlinearity and initial ovalization ignored.

unbonded flexible risers;pressure;strain;nonlinearity;quasi-static;lay angle

0 Introduction

Unbonded flexible risers are composed of interlocked carcass,pressure armor layer,tensile armor layers,anti-friction tapes and outer sheath,slippage can occur between tensile armor layers and adjacent layers[1-4].Flexible risers have been largely used by the deep sea oil and gas industry,they must withstand large internal and external pressures.

Analytical models to predict the behavior of unbonded flexible risers are based on equilibrium equations of forces and displacement of layers[1,5-7].For numerical models,because of time consuming computation and convergence problem,carcass and pressure armor layer are simplified as hollow cylindrical structures rather than helical strips,lay angles and cross-sectional profiles are completely ignored in the simplified finite element model[1,8-9],it is adverse to stresses analysis,collapse buckling study and burst prediction of interlocked layers.Kebadze presented a set of equilibrium equations for different layers,all unknowns are solved by combining with geometric relationships between adjacent layers,it is shown that internal pressure versus strain curve is linear[9].Neto developed two finite element models to predict collapsebuckling of interlocked carcass under external pressure,one is the full 3D model which took lay angle and cross-sectional profile into consideration,the other is the ring 3D model with lay angle effect neglected[10].Interesting results are found that the two different finite element models give the same results,initial ovalization and material nonlinearity of carcass have a great impact on buckling load[10-11].

Although symmetrical behavior of unbonded flexible riser has been dealt in previous work,current approaches still suffer from following defects：(1)Analytical models are limited in small displacements and strains,with friction,material nonlinearity and initial manufacturing defects ignored;(2)Due to irregular cross-sectional profiles,stresses in carcass and pressure armor layer cannot be reliably predicted by analytical and simplified finite element models;(3)Lay angle effect on collapse buckling of interlocked carcass and pressure armor layer is negligible,but impact of lay angle effect of interlocked layers on strains of the riser is not discussed.

To make up above defects,a numerical model which takes cross-sectional profiles,lay angles of carcass and pressure armor layer into account is presented,Abaqus/Explicit quasistatic simulation and mass scaling are adopted to avoid convergence problem and time consuming computation.Geometric,contact and material nonlinearities are all considered in the finite element model.Strains of an eight-layer unbonded flexible riser under pressures are predicted,impacts of boundary conditions and lay angles of pressure armor layer,tensile armor layers on strains are analyzed.

1 Analytical model

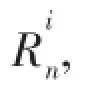
Following assumptions are made in analytical model[1,6-7]：

(1)Displacements and strains are small;

(2)Because all layers are fixed by end fittings,so all layers have the same axial variation△L and twist△Φ;

(3)Contact pressures and strains are uniformly distributed along the riser length;

(4)Thickness variations of carcass and pressure armor layer are ignored;

(5)Initial manufacturing defects are ignored.

Equilibrium equations of carcass and pressure armor layer are expressed as follows[7]：

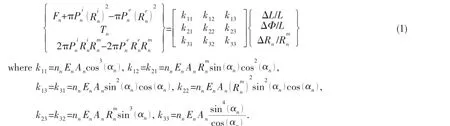
Equilibrium equations of polymeric layers and tensile armor layers are expressed as follows[7]：

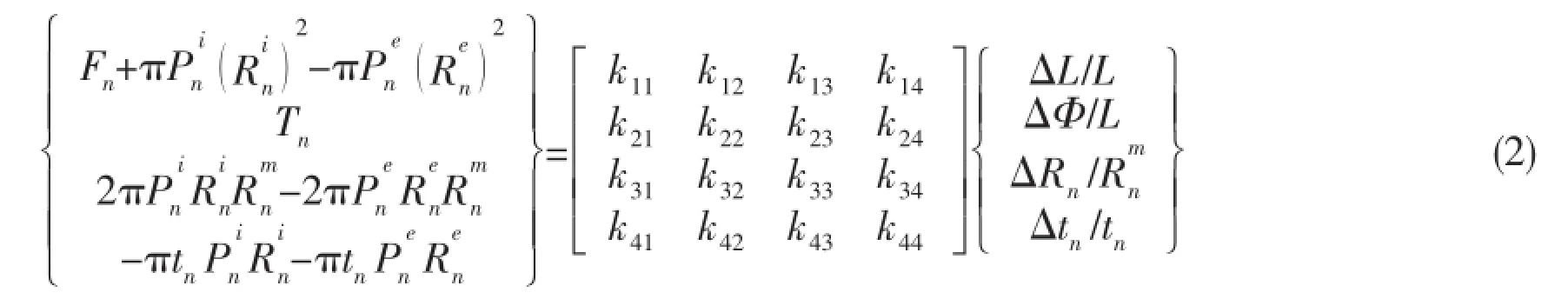
For polymeric layers,coefficients in Eq.(2)are expressed as[9]：

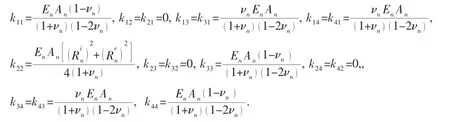
For tensile armor layers,coefficients in Eq.(2)are expressed as[7]：

From above equations,we can obtain Eq.(3)and Eq.(4)[1,6-7]：

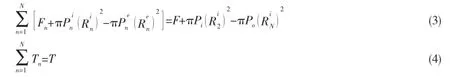
Geometric relationship between adjacent layers can be combined to solve all unknowns, if the n-th and(n+1)-th layers are in contact,then following equation can be obtained[7]：

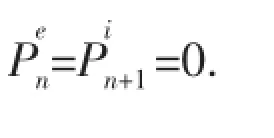
2 Numerical model

2.1 Flexible riser data

An eight-layer unbonded flexible riser is chosen for the case study,data of component layers are listed in Tab.1[12-13].

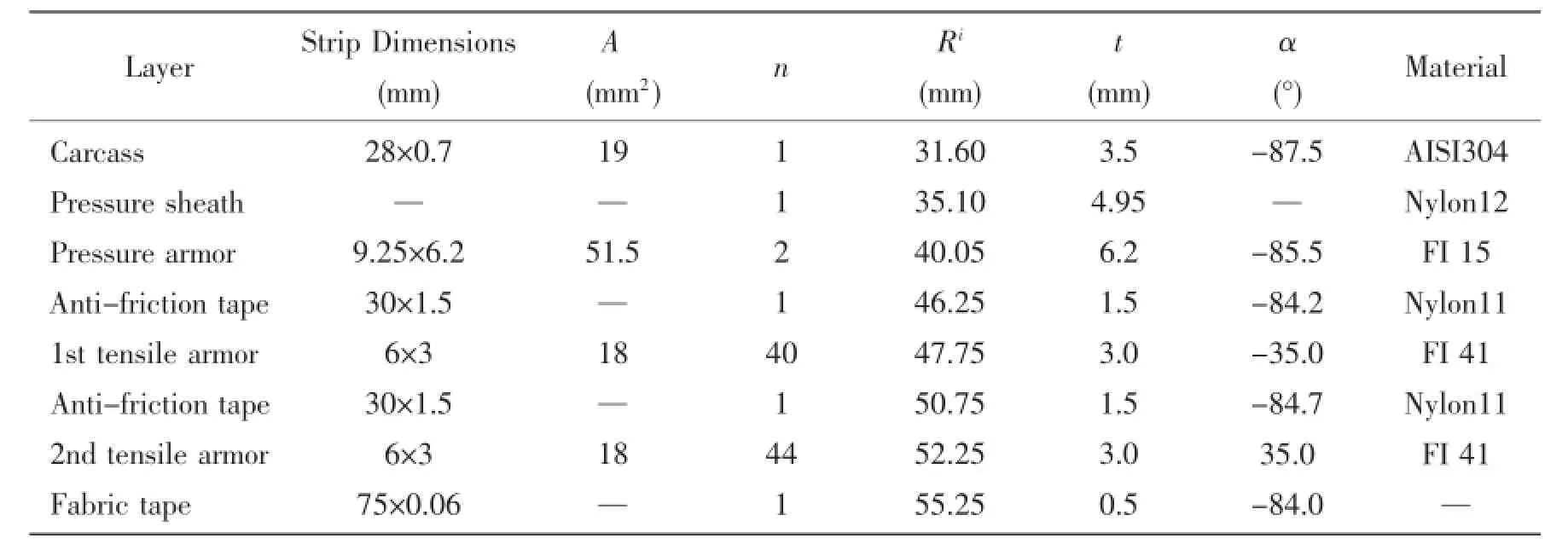
Tab.1 Unbonded flexible riser data

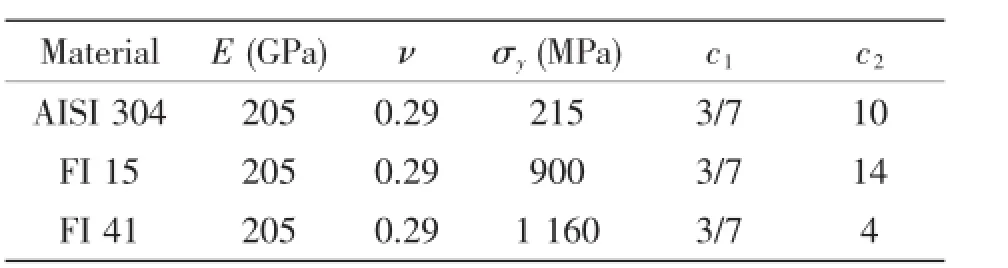
Nonlinear material behavior of metallic layers is modeled,the strain versus stress relationship is expressed by the Ramberg-Osgood curve：

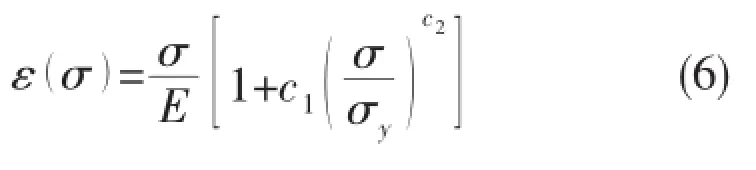
Tab.2 Nonlinear material properties of metallic layers

where σyis the yield stress of the material,material properties are listed in Tab.2.

Material properties of polymeric layers are listed as below：for Nylon 12,E=284 MPa,ν= 0.3;for Nylon 11,E=301 MPa,ν=0.3;for fabric tape,E=600 MPa,ν=0.3[12].

2.2 Numerical model

Cross-sectional profiles and lay angles of carcass and pressure armor layer are considered in the numerical model.The length of the numerical model is 1.0 m,which equals abouttwice the length of one pitch in the outer tensile armor layer,as suggested by the manufacturer[1].Finite element model of the typical unbonded flexible riser is shown in Fig.1 by hiding parts of the finite element model along the z-axis direction.

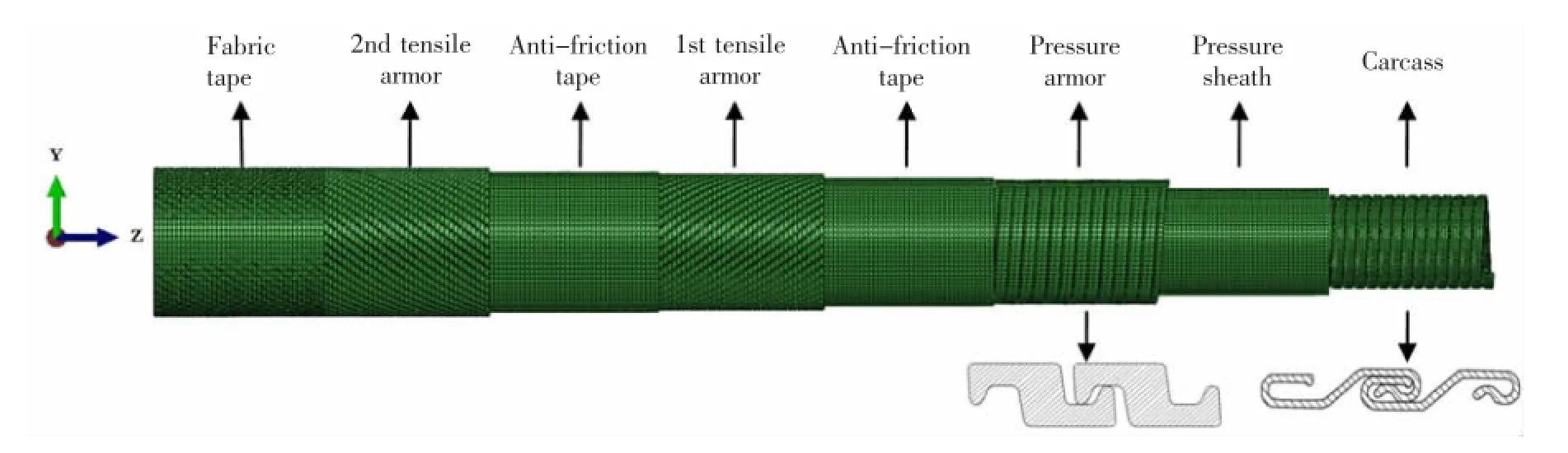
Fig.1 Finite element model of the unbonded flexible riser

2.3 Contact and time-step control

General contact is adopted to simulate tangential and normal behavior of contact,the coefficient of friction is taken as 0.1,as given in experimental results[14].Hard contact is chosen to prevent penetration[1,8-9].Two reference points named RP1and PR2are created at(0 m,0 m, 0 m),(0 m,0 m,1 m),respectively.Defining(0 m,0 m,0 m)is the bottom end of the riser,(0 m,0 m,1 m)is the top end of the riser.All nodes at the bottom section of each layer are selected as set 1,all nodes at the top section of each layer are selected as set 2.RP1 is coupled with set 1,PR2 is coupled with set 2,respectively,the coupling type is kinematic.

Due to contact,geometric nonlinearity and time consuming computation,the analysis is conducted by Abaqus/Explicit quasi-static simulation and mass scaling.The minimum time increment is set as 5.0×10-7s.

Three ratios should be carefully monitored to determine whether the results are reliable or not.They are the ratio of kinetic energy to internal energy,the ratio of kinetic energy to elastic strain energy,the ratio of artificial strain energy to internal energy,all ratios should not be greater than 5%[15].

3 Case study

3.1 Load cases

To study the impact of boundary condition(BC)of RP2on the behavior of the unbonded flexible riser under pressures,internal and external pressures are applied on the riser,respectively.Load cases are listed in Tab.3,because of the non-watertight of interlocked carcass,internal pressure is applied on the inner surface of pressure sheath,external pressure is applied on the outer surface of fabric tape.

To analyze lay angle effect on strains,αpand αtwhich indicate lay angles of pressure armor and tensile armors layers are changed with the same number of tendons,respectively.A ring model is also developed,in which pressure armor layer is developed with the same crosssectional profile,but lay angle equals 90°,it is modeled as a ring rather than helical strips,distance between rings is half pitch of pressure armor layer.Data of other layers remain unchanged.Internal and external pressures of 30 MPa are applied on the riser,respectively.Load cases are listed in Tab.4.

Tab.3 Load cases of different BC

Tab.4 Load cases of different lay angles

3.2 Results of different boundary conditions

Strains of load cases shown in Tab.3 are listed in Tab.5.It can be seen that compared to elongation,boundary condition of PR2has greater impact on twist.Difference between analytical and numerical results is mainly caused by following reasons：(1)Friction coefficient which is set as 0.1 in numerical model cannot be considered in analytical model;(2)Contact pressures and strains are assumed to be uniformly distributed along the riser length in analytical model,which are not suitable for numerical model;(3)Nonlinear material behavior is ignored in analytical model.

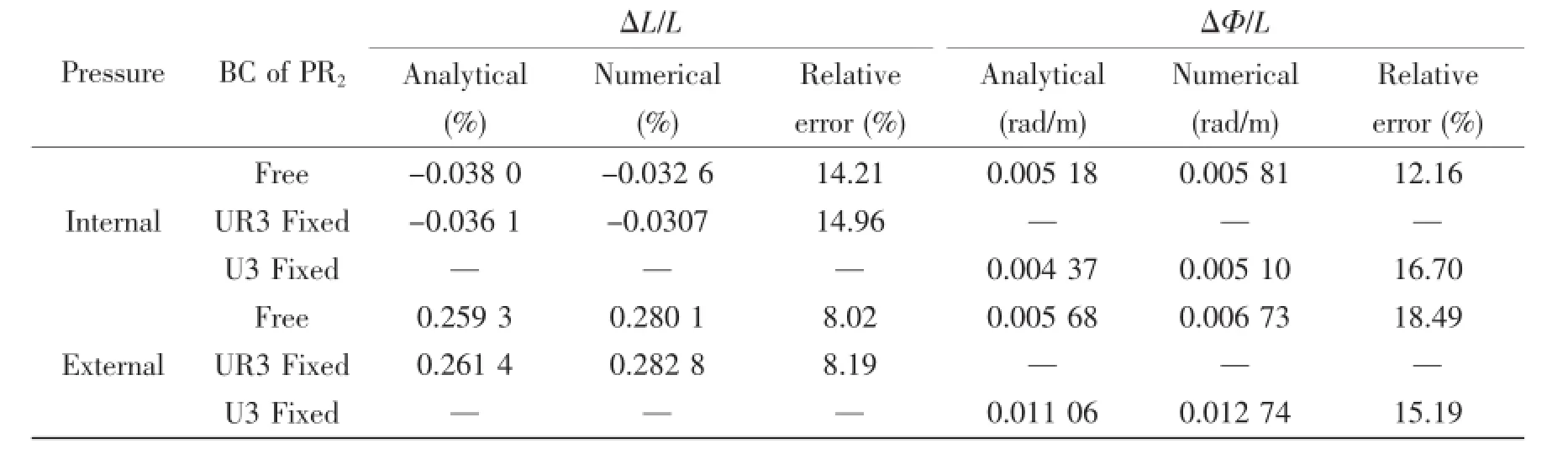
Tab.5 Results of strains under pressures

Because trends of strains are the same when the flexible riser under internal and external pressures,only internal pressure-elongation and internal pressure-twist curves are shown in Figs.2-4.As can be seen except the computational instability resulting from contact and geometric nonlinearity at the initial time,both analytical and numerical results show that strains vary linearly with internal pressure.

3.3 Results of different lay angles of pressure armor layer

Strains of different lay angles of pressure armor layer under pressures are listed in Tab.6. It is shown that lay angle of pressure armor layer has great impact on strains.Meanwhile,compared to αp=-85.5°,elongation and twist got from the ring model under internal pressure decrease by about 15.64%and 87.26%,respectively;twist got from the ring model under external pressure sharply increases by 105.65%.

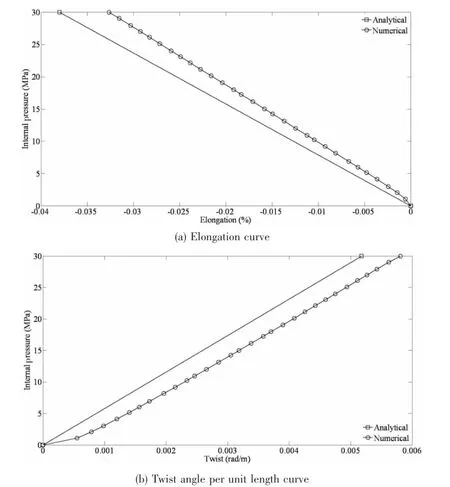
Fig.2 Internal pressure versus strain curves with end free

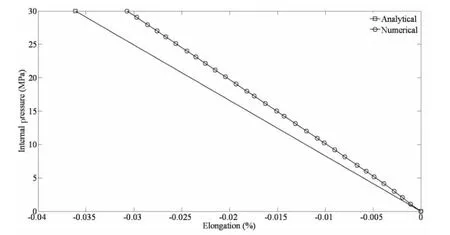
Fig.3 Internal pressure versus elongation curve with end prevented from rotating

Fig.4 Internal pressure versus twist curve with end prevented from moving axially

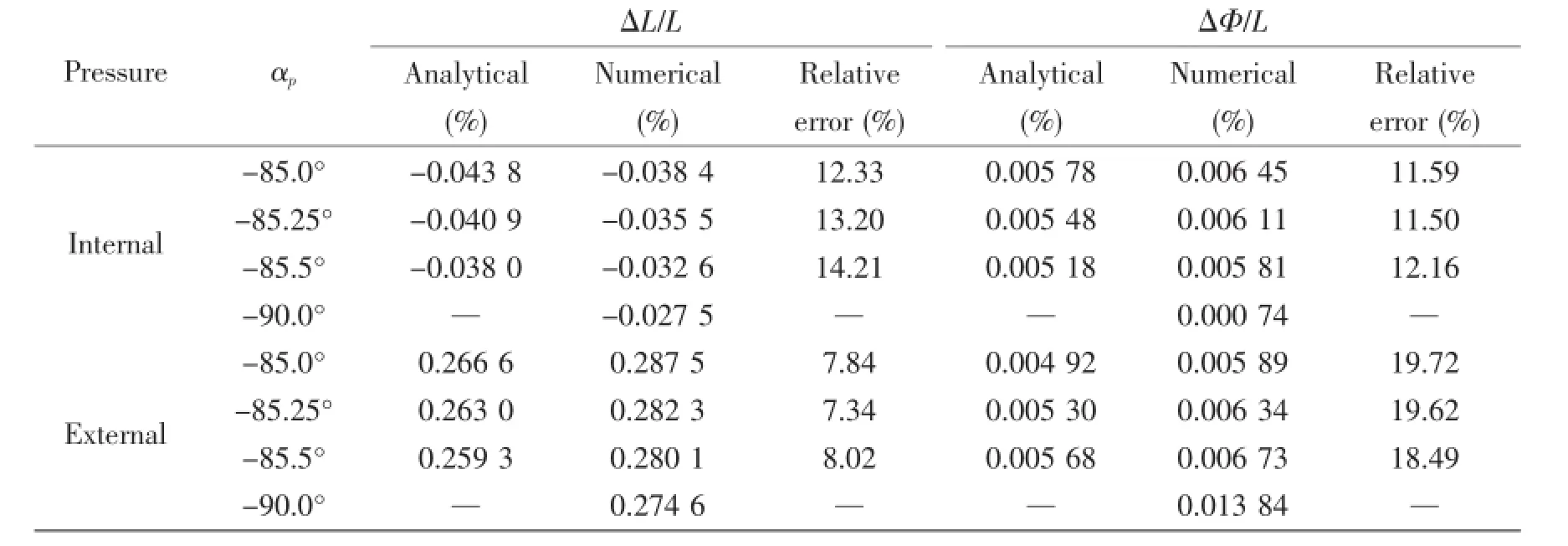
Tab.6 Strains of different lay angles of pressure armor layer under pressures

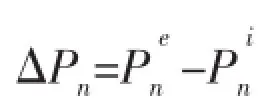
Tab.7 Contact pressures between layers with end free

3.4 Results of different lay angles of tensile armor layers

Strains of different lay angles of tensile armors under pressures are listed in Tab.8.It can be seen from Tab.7 and Tab.8,although radial pressures that tensile armor layers withstand are not the maximum,lay angles of tensile armor layers have great impact on both elongation and twist.

Tab.8 Strains of different lay angles of tensile armor layers under pressures

4 Conclusions

Simplified numerical models of unbonded flexible risers can not take lay angel effect of interlocked layers into consideration,which has great impact on behavior of unbonded flexible risers under pressures.Meanwhile,friction,material nonlinearity are completely ignored in analytical models.To avoid defects of analytical model and simplified numerical models,a very detailed numerical model of an eight-layer unbonded flexible riser is developed and verified.

It is shown that under pressures,by contrast with elongation,boundary condition has greater impact on twist;lay angle effect of pressure armor layer,which can be ignored in collapse buckling study,must be considered in strain analysis when risers subject to pressures; lay angle of tensile armor layers has great influence both on axial elongation and twist.

[1]Bahtui A.Development of a constitutive model to simulate unbonded flexible riser pipe elements[D].Ph.D.thesis,Brunel University,2008.

[2]Yue Q,Lu Q,Yan J,Zheng J,Palmer A.Tension behavior prediction of flexible pipelines in shallow water[J].Ocean Engineering,2013,58：201-207.

[3]de Sousa J R M,Viero P F,Magluta C,Roitman N.An experimental and numerical study on the axial compression response of flexible pipes[J].Journal of Offshore Mechanics and Arctic Engineering,2012,134(3)：paper No.031703.

[4]Vaz M A,Rizzo N A S.A finite element model for flexible pipe armor wire instability[J].Marine Structures,2011,24(3)：275-291.

[5]Ramos R,Pesce C P.A consistent analytical model to predict the structural behavior of flexible risers subjected to combined loads[J].Journal of Offshore Mechanics and Arctic Engineering,2004,126：141-146.

[6]Féret J J,Bournazei C L.Calculation of stresses and slip in structural layers of unbonded flexible pipes[J].Journal of Offshore Mechanics and Arctic Engineering,1987,109(3)：263-269.

[7]Kebadze E.Analytical modelling of unbonded flexible pipe cross-sections[D].PhD thesis,South Bank University,2000.

[8]Alfano G,Bahtui A,Bahai H.Numerical derivation of constitutive models for unbonded flexible risers[J].International Journal of Mechanical Sciences,2009,51(4)：295-304.

[9]Bahtui A,Bahai H,Alfano G.A finite element analysis for unbonded flexible risers under torsion[J].Journal of Offshore Mechanics and Arctic Engineering,2008,130(4)：paper No.041301.

[10]Neto A G,de Arruda Martins C.A comparative wet collapse buckling study for the carcass layer of flexible pipes[J].Journal of Offshore Mechanics and Arctic Engineering,2012,134(3)：paper No.031701.

[11]Tang Minggang,Wang Ye,Yan Jun,Yue Qianjin.Finite element analysis for collapse of flexible pipes carcass[J].Journal of Harbin Engineering University,2013,34(9)：1-5.(in Chinese)

[12]Witz J A.A case study in the cross-section analysis of flexible risers[J].Marine Structures,1996,9(9)：885-904.

[13]Custodio A B,Vaz M A.A nonlinear formulation for the axisymmetric response of umbilical cables[J].Applied Ocean Research,2002,24(1)：21-29.

[14]Saevik S,Berge S.Fatigue testing and Analytical studies of two 4 in flexible pipes[J].Engineering Structures,1995,17 (4)：276-292.

[15]Hibbitt,Karlsson,Sorensen.ABAQUS Analysis User’s Manual[M].Hibbitt,Karlsson&Sorensen,Inc,2010.

壓力載荷下非粘結(jié)柔性立管應(yīng)變影響因素分析

任少飛，唐文勇，薛鴻祥
（上海交通大學(xué)海洋工程國家重點實驗室，上海200240）

基于Abaqus/Explicit準(zhǔn)靜態(tài)和質(zhì)量放大方法研究了一類典型非粘結(jié)柔性立管在壓力載荷作用下應(yīng)變響應(yīng)特性，對影響立管整體軸向延伸率和繞軸向扭轉(zhuǎn)角度的因素進行了分析。數(shù)值模型計入金屬層實際截面形狀、鋪設(shè)角度以及幾何、接觸、材料非線性。計算結(jié)果表明：數(shù)值解與理論值吻合較好；立管端部邊界條件對軸向延伸率影響不大但對繞軸向扭轉(zhuǎn)角度影響較大；抗壓鎧裝層為徑向壓力主要受力構(gòu)件，其鋪設(shè)角度雖然對壓潰性能不大，但在應(yīng)變分析中不可忽略；拉伸鎧裝層鋪設(shè)角度對應(yīng)變影響同樣較大。文中數(shù)值方法可彌補理論方法限定在小位移、小變形范圍，無法計入層間摩擦、材料非線性及初始制造橢圓率等缺陷。

非粘結(jié)柔性立管；壓力；應(yīng)變；非線性；準(zhǔn)靜態(tài)；鋪設(shè)角度

P751

：A

任少飛（1986-），男，上海交通大學(xué)博士研究生；

1007-7294（2015）12-1525-10

P751

：A

10.3969/j.issn.1007-7294.2015.12.009

唐文勇（1970-），男，博士，上海交通大學(xué)教授，博士生導(dǎo)師，通訊作者；

薛鴻祥（1981-），男，博士，上海交通大學(xué)副教授。

Received date：2015-06-17

Foundation item：Supported by Fund of State Key Laboratory of Ocean Engineering(Grant No.GKZD010059-6)

Biography：REN Shao-fei(1986-),male,Ph.D.student;TANG Wen-yong(1970-),male,Ph.D.,professor/tutor, E-mail：wytang@sjtu.edu.cn.