小攻角下航行體三維非定常空泡形態理論預示方法

程少華，權曉波，于海濤，翟章明，王占瑩（北京宇航系統工程研究所，北京100076）

小攻角下航行體三維非定常空泡形態理論預示方法

程少華，權曉波，于海濤，翟章明，王占瑩
（北京宇航系統工程研究所，北京100076）

小攻角下水下航行體高速運動時會形成不對稱、非定常空泡，空泡形態是水下流體動力及彈道設計的主要依據。該文基于空泡獨立膨脹原理，考慮橫流對獨立空泡發展的影響，建立了帶攻角狀態下空泡形態理論計算模型。針對典型工況開展計算獲得了航行體迎背流面空泡長度、空泡壓力變化過程，并與試驗數據進行比對以驗證模型的合理性。

空泡形態；局部空化；獨立膨脹原理；流體動力；非定常

0 引 言

當航行體在水中高速運動時，其表面某些部位的壓力低于水的飽和蒸汽壓而出現空化現象，將使得空泡附著于航行體的表面。隨著航行體速度和所處位置的不斷變化，空化處的空泡數也隨之發生改變，使得空化形成的空泡形態呈現出隨時間變化的非定常特征。特別是當來流與航行體存在一定的攻角時，迎背流面的空泡長度也有所不同，使得空泡呈現出三維特性。航行體空泡非定常發展及不對稱性將改變航行體表面的壓力分布，從而對其水下運動軌跡和受力特征產生較大影響。準確預示非定常三維空泡形態是空泡繞流流體動力設計的基礎，也是航行體水下運動軌跡設計的前提。

小攻角下航行體空泡流動是典型的非定常多相流問題，對其進行建模和預示具有較大的難度。早期的研究主要以基于勢流理論的邊界元方法為主，通過假設汽液兩相之間具有明確的界面、空泡內壓力恒定，且假定空泡在物體表面的閉合形式，可根據動力學及運動學邊界條件最終確定空泡的形態和位置。Kinnas[5]通過在水翼和空泡表面分布法向偶極子和源，假設空化區的速度為沿著水翼的長度變化的變量，采用基于速度勢的邊界元方法對水翼三維空泡繞流問題進行了研究，冷海軍[6]、傅慧萍[7]等在空泡尾部采用壓力恢復模型，求解給定空泡數下軸對稱體的定常空泡形態，張忠宇等[8]將該方法擴展至三維帶攻角狀態空泡形態計算，并分析了空化數、攻角以及錐角對三維空泡形態的影響規律。總體上來看基于勢流理論的邊界元方法主要針對定常狀態二維或三維空泡形態開展計算。

近些年來，隨著計算技術和數值模擬方法的不斷發展，通過求解N-S方程的數值CFD技術在空泡繞流計算中獲得廣泛應用。通過研究多相流模型、湍流模型、空化模型對空泡形態的影響規律，結合與試驗數據的比對建立了適用于不同條件下空泡流的計算方法。權曉波等[9]采用均相平衡流模型、Singhal模型及標準k-ε湍流模型獲得了定常狀態大攻角下與試驗結果吻合較好的空泡形態，分析了不同攻角、空化數對彈體受力的影響，王一偉等[10]采用均相平衡流模型、Singhal模型及RNG k-ε湍流模型獲得了航行體水下及出水過程中空泡非定常發展及潰滅特征。數值CFD方法可獲得相對較為準確的空泡流場特征，但針對非定常空泡流的計算所需時間較長。

針對非定常空泡形態的預示，工程上確定空泡形態常采用Logvinovich[1]提出的“空泡獨立膨脹原理”。以此為基礎，Paryshev[2]建立了一組描述通氣空泡的非線性遲滯微分方程組（Delay Differential E-quations，簡寫為DDEs），并采用線性理論分析了多種空泡類型的穩定性。Kirschner[3]針對Paryshev的模型提出了一種有效的求解方法，獲得了航行體水平運動時的超空泡形態變化特征。在國內，陳瑋琪等[11]基于“空泡獨立膨脹原理”導出了非定常垂直空泡長度的計算公式，并給出了出水空泡潰滅高壓作用的條件和判據，張學偉等[12]基于“空泡獨立膨脹原理”給出了通氣空泡下空泡形態和壓力的理論計算方法。現有的基于"獨立膨脹原理"的非定常空泡形態理論計算僅針對二維軸對稱狀態，對于三維空泡形態的理論計算尚無成熟模型可供借鑒。

針對小攻角狀態下三維非定常空泡形態的理論預示問題，本文以空泡獨立膨脹原理為基礎，考慮橫流對獨立空泡發展的影響，建立了帶攻角狀態下空泡非定常發展理論計算模型，并與試驗數據進行比對以驗證模型的合理性。該方法可大大提高計算效率，便于采用理論分析的方式獲取影響三維空泡形態的主要要素，供工程設計人員參考。

1 三維非定常空泡預示模型建立

1.1 獨立膨脹原理

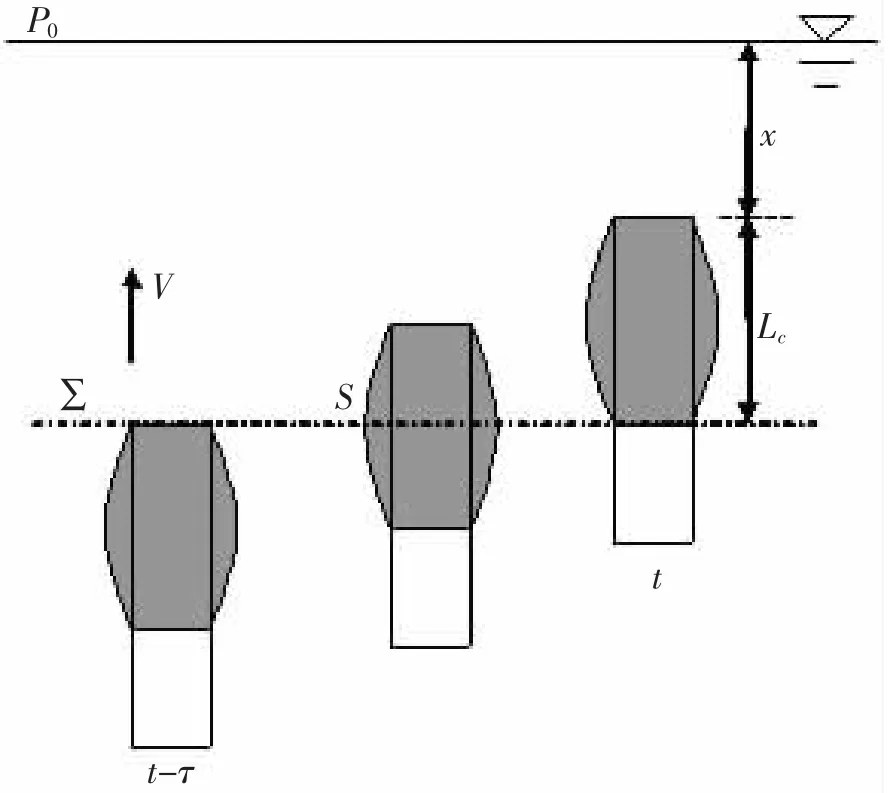
圖1 二維軸對稱空泡發展示意圖Fig.1 Sketch map for 2-D symmetric cavity development

式中：壓力p∞=p0+ρg，為截面Σ所處的靜壓，p0為水面大氣壓，x為空泡初生位置距離水面高度，Lc為空泡長度。pc為空泡泡壓，隨時間不斷變化。k為經驗系數，，a為與彈體頭型、空化數相關的常數。

在初始時刻，截面S滿足方程：

式中：R0為航行體柱段半徑；Cx為航行體頭錐段阻力系數。

圖1所示為二維軸對稱空泡發展示意圖。

1.2 帶攻角下獨立膨脹原理

考慮航行體在水下以速度V（t）、攻角α向水面運動，以截面Σ為研究對象，根據“空泡獨立膨脹原理”由于該截面空泡周圍靜壓相同，故而空泡的橫截面仍為圓形，但由于橫向速度分量的影響，空泡的圓心也隨之運動。

將航行體速度V沿彈體分解為軸向速度Vy和橫向速度Vx，并假定兩個方向的運動對空泡的影響是相互獨立的，建立帶攻角狀態下的空泡獨立膨脹方程：

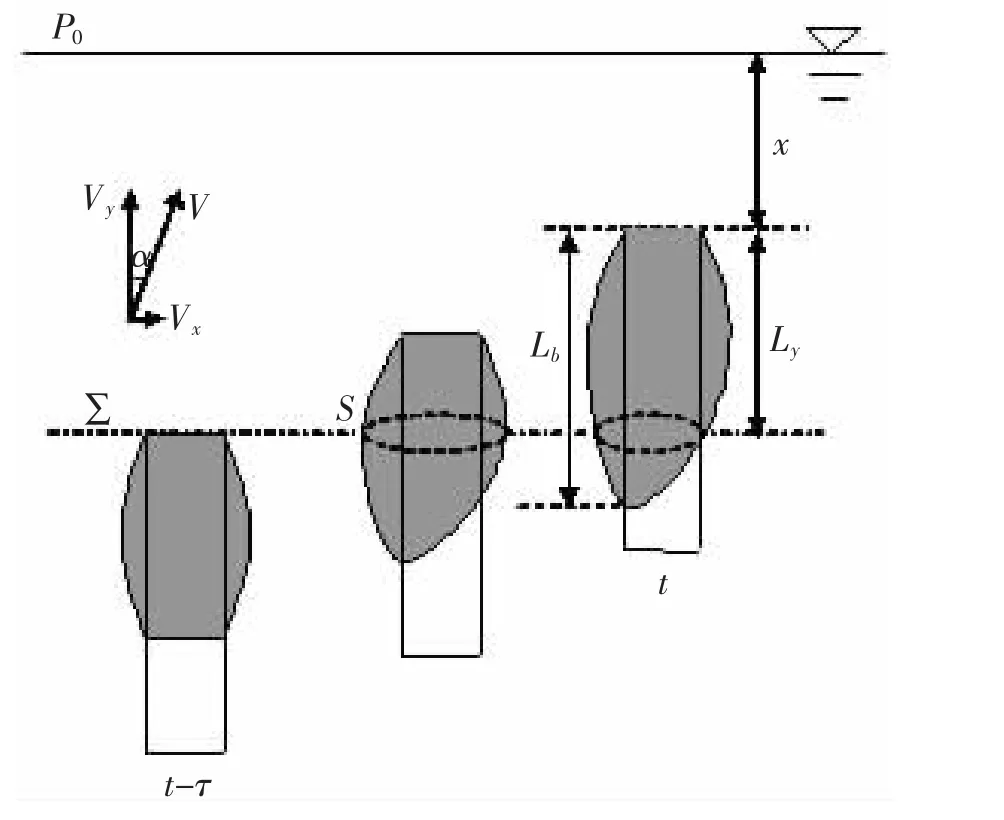
圖2 三維有攻角下運動空泡發展示意圖Fig.2 Sketch map for 3-D symmetric cavity development

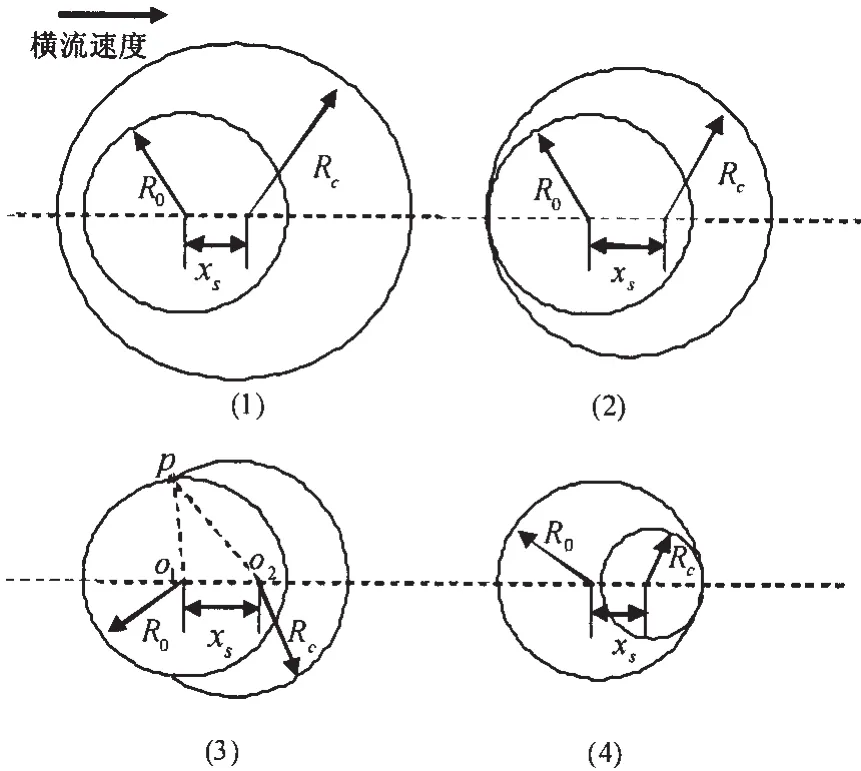
圖3 空泡橫截面與航行體相對位置關系圖Fig.3 Relative position for cavity section and body

式中：xs（t）為t時刻截面Σ圓心的橫移量。Vx（t）為t時刻航行體運動速度的橫向分量，滿足Vx=Vsin （α），α為來流相對航行體攻角。

圖2所示為三維有攻角下運動空泡發展示意圖。

1.3 空泡閉合模型判定

根據橫截面空泡面積和橫移量的變化過程，可建立空泡橫截面與航行體的相對位置關系，如圖3所示。其中R0為航行體半徑，Rc為空泡橫截面半徑，xs為空泡橫截面圓心的偏移量。

當空泡截面、航行體截面的相對位置關系如圖3（1）所示，空泡橫截面完全包裹了航行體橫截面，此時滿足如下表達式：

式中：Q（ξ, t）為t時刻ξ截面有效橫截面積，xs（ξ, t）為t時刻ξ截面橫移量。

當空泡截面、航行體截面的相對位置關系如圖3（2）所示，空泡迎流面剛剛包裹了航行體橫截面，迎流面空泡厚度為零，此時滿足如下表達式：

式中：ξy（t）為滿足迎流面空泡厚度為0的截面序號；Q（ξy（t）,t）為t時刻ξy（t）截面有效橫截面積，Ly（t）為t時刻迎流面空泡長度，Ts為數值求解時間步長。

當空泡截面、航行體截面的相對位置關系如圖3（3）所示，航行體背流面為空泡區，迎流面為全濕流區，空泡橫截面未能對彈體進行有效包裹，此時滿足如下表達式：

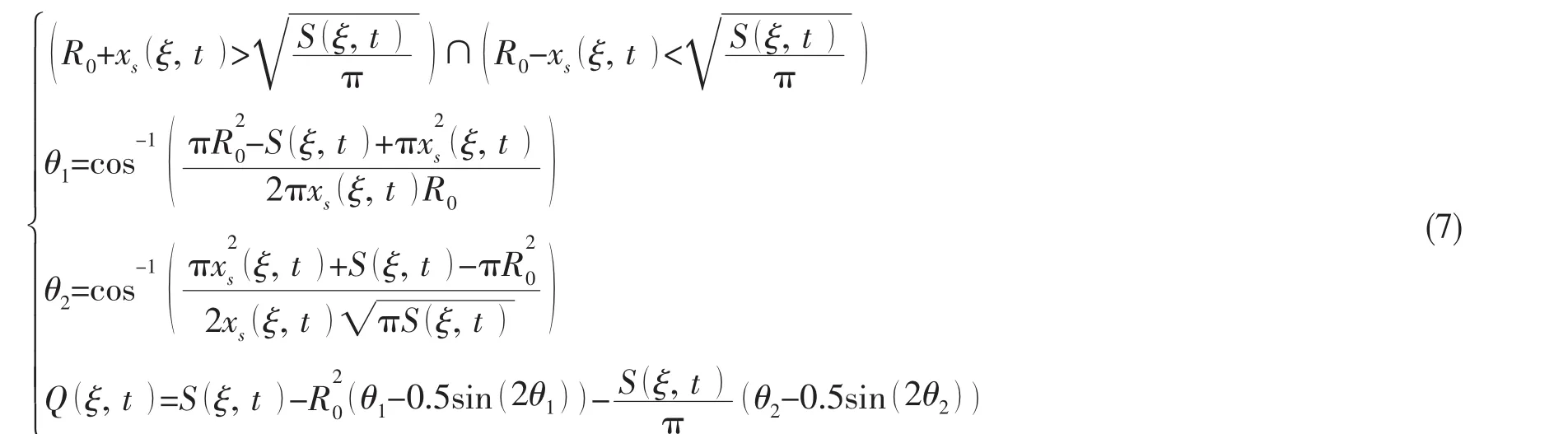
式中：θ1為空泡與航行體重合區在航行體圓截面上對應的圓心角的一半，如圖3（3）所示的∠po1o2；θ2為空泡與航行體重合區在空泡圓截面上對應的圓心角的一半，如圖3（3）所示的∠po2o1；Q ——ξ,t）為t時刻ξ截面有效橫截面積。

當空泡截面、航行體截面的相對位置關系如圖3（4）所示，空泡背流面與航行體橫截面相切，背流面空泡厚度為零，本時間步長內計算截至。此時滿足如下表達式：

式中：ξb（t）為滿足背流面空泡厚度為0的截面序號；Q（ξb（t）,t）為t時刻ξb（t）截面有效橫截面積；Lb（t）為t時刻背流面空泡長度；Ts為數值求解時間步長。

從而最終得到空泡體積Q（t）為：

式中：Q（i,t）為t時刻第i截面有效橫截面積；Ts為數值求解時間步長。

1.4 質量守恒方程

空泡的非定常發展過程需滿足質量守恒方程，具體方程形式為：

式中：m（t）為t時刻空泡氣體的質量；c1為空泡氣體的分子量；in為通入空泡的質量流率，為計算時設定值，當自然空化時˙in=0；˙out為空泡泄氣質量流率，參考Logvinovich給出的泄氣經驗公式，得到：

式中：kout≈0.01，為空泡泄氣常數；σv為自然空化數；σ為空泡空化數。

2 模型特殊解

假定航行體在水下運動的速度V恒定、攻角α保持為常值，且空泡壓力保持不變，對有攻角下迎背水面泡長差進行求解。

根據（3）式和迎流面空泡長度截止條件，可得到迎流面空泡截止時刻Δty滿足表達式：

解得：

同理，可得到背流面空泡截止時刻Δtb的表達式：

進而得到迎背流面泡長差的表達式為：

上式表明當彈體處于勻速運動狀態下且泡壓不變時，迎背流面泡長差與彈體的攻角近似成正比關系。

3 預示方法驗證

為了檢驗模型特殊解（17）式、非定常空泡形態預示方法（3）式的有效性，分別采用數值CFD計算結果、航行體垂直發射水下彈射試驗進行驗證。

采用數值CFD計算數據對本文第2章模型特殊解下（3）式進行驗證。本文選用參考文獻[9]中不同攻角下迎背流面壓力系數CFD計算結果，如圖4所示，該數值CFD計算結果已經經水洞試驗所證實。通過對圖4壓力系數的判讀，得到4°攻角下迎背水面泡長差相對彈長的歸一化長度為0.089，8°攻角下迎背水面泡長差相對彈長的歸一化長度為0.17。

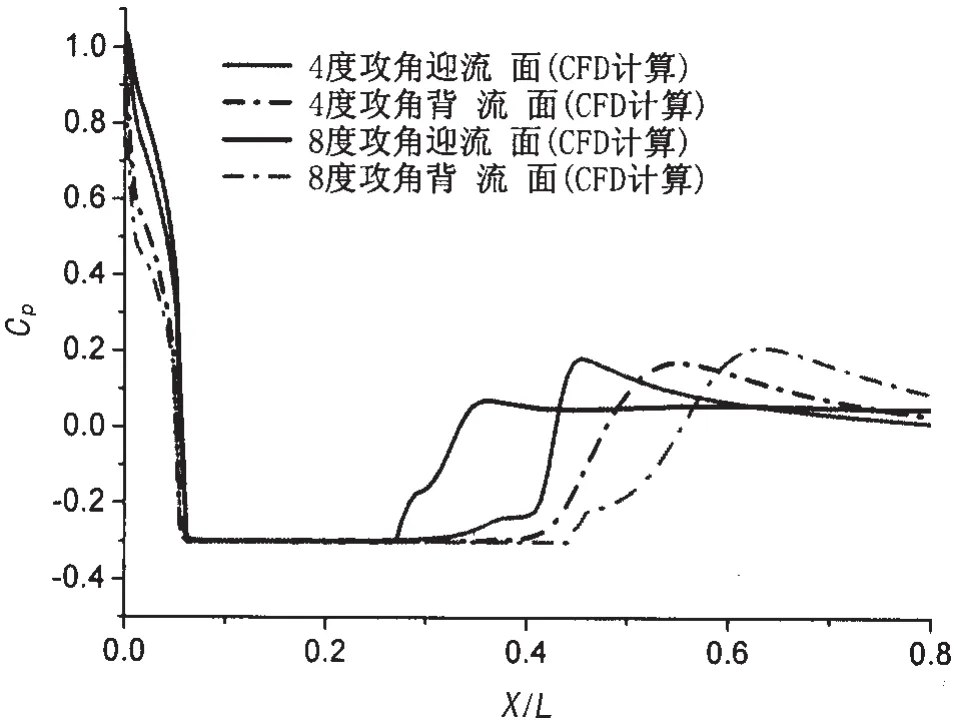
圖4 數值CFD壓力系數結果（σ=0.3）Fig.4 CFD results for pressure coefficient(σ=0.3)

根據（17）式，計算得到4°攻角下迎背水面泡長差相對彈長的歸一化長度為0.084 3，8°攻角下迎背水面泡長差相對彈長的歸一化長度為0.169。可見（17）式計算結果與數值CFD仿真結果得到不同攻角下泡長差量值吻合較好，且體現了泡長差隨攻角近似呈正比關系，表明了（17）式的正確性。

通過開展水下垂直發射彈射試驗對有攻角下非定常運動空泡形態計算方法進行驗證。為了模擬帶攻角的運動，航行體垂直向上彈射時給定初始橫向速度。在航行體迎背水面布置壓力傳感器，通過壓力測量數據判定非定常空泡長度和壓力的變化歷程。

同步開展空泡形態理論預示，相關計算方法如參考文獻[12]。聯合獨立膨脹原理和質量守恒方程，獲得迎背水面空泡長度、空泡壓力隨時間的變化歷程，并與試驗數據結果進行比對，見圖5、圖6所示。從比對結果來看，理論預示值與試驗測量數據吻合良好，表明本方法的合理性。

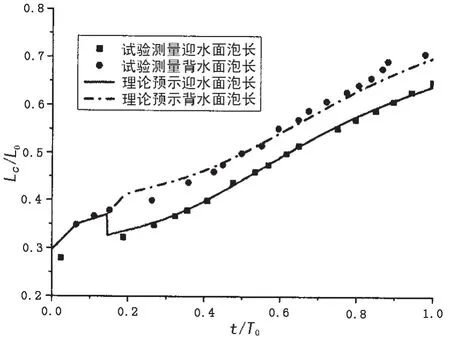
圖5 理論預示泡長與試驗結果比對Fig.5 Comparison of theoretical and experimental results for cavity length

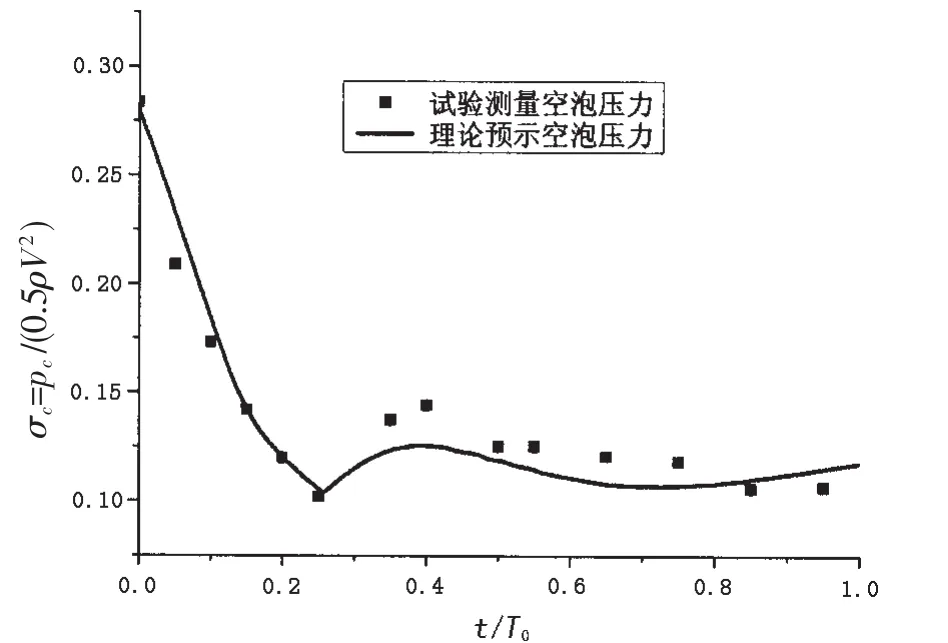
圖6 理論預示泡壓與試驗結果比對Fig.6 Comparison of theoretical and experimental results for cavity pressure

4 結 論

本文通過在Logvinovich獨立膨脹原理中引入橫流影響，將二維軸對稱空泡理論計算模型擴展至三維帶攻角下理論計算情形，獲取了水下垂直發射迎背流面空泡非定常發展過程。通過對空泡形態理論預示方法進行研究表明，定常狀態下迎背流面空泡長度差與攻角密切相關。空泡長度差隨攻角的增大而增大，并呈現出近似線性關系；非定常三維空泡迎背流面長度和壓力計算結果與試驗數據吻合較好，表明本方法可適用于小攻角下非定常空泡流計算。

[1]Logvinovich G V.Hydrodynamics of flows with free boundaries[M].New York:Halsted Press,1973.

[2]Paryshev E V.Approximate mathematical models in high-speed hydrodynamics[J].Journal of Engineering Mathematics, 1978,55:41-64.

[3]Kirschner I N.Implementation and extension of Paryshev’s model of cavity dynamics[C]//Proc.of SuperFAST’2008.Saint-Petersburg,Russia,2008.

[4]Vasin A D.The principle of independence of the cavity sections expansion(Logvinovich’s Principle)as the basis for investigation on cavitation flows[C]//VKI Special Course on Supercavitating Flows.Brussels:RTO-AVT and VKI,2001:RTOEN-010(8):105-131.

[5]Kinnas S A,Fine N E.A numerical nonlinear analysis of the flow around 2-D and 3-D partially cavitating hydrofoils[J].J Fluid Mech,1993,254(9):151-181.

[6]冷海軍,魯傳敬.軸對稱體的局部空泡流研究[J].上海交通大學學報,2002,36(3):395-398. Leng Haijun,Lu Chuanjing.Study on partially cavitating flow of an axisymmetric body[J].Journal of Shanghai Jiaotong U-niversity,2002,36(3):395-398.

[7]傅慧萍,李福新.回轉體局部空泡繞流的非線性分析[J].力學學報,2002,34(2):278-285. Fu Huiping,Li Fuxin.A numerical analysis of the flow around a partially-cavitating axisymmetric body[J].Acta Mechanica Sinica,2002,34(2):278-285.

[8]張忠宇,姚熊亮,張阿漫.小攻角下三維細長體定常空化形態研究[J].物理學報,2013,62(20):301-309. Zhang Zhongyu,Yao Xiongliang,Zhang Aman.Cavitation shape of the three-dimensional slender at a small attack angle in a steady flow[J].Acta Phys.Sin,2013,62(20):301-309.

[9]權曉波,魏海鵬,孔德才,等.潛射導彈大攻角空化流動特性計算研究[J].宇航學報,2008,29(6):1701-1705. Qüan Xiaobo,Wei Haipeng,Kong Decai,et al.Numerical simulation on cavitation of submarine launched missile’s surface at large angles of attack[J].Journal of Astronautics,2008,29(6):1701-1705.

[10]王一偉,黃晨光,杜特專,等.航行體有攻角出水全過程數值模擬[J].水動力學研究與進展,A輯,2011,26(1):48-57. Wang Yiwei,Huang Chenguang,Du Tezhuan,et al.Numerical simulation of a submerged body exiting from water with an attack angle[J].Journal of Hydrodynamics,Ser.A,2011,26(1):48-57.

[11]陳瑋琪,王寶壽,顏 開,等.空化器出水非定常垂直空泡的研究[J].力學學報,2013,45(1):76-82. Chen Weiqi,Wang Baoshou,Yan kai,et al.Study on the unsteady vertical cavity of the exit-water cavitor[J].Acta Mechanica Sinica,2013,45(1):76-82.

[12]張學偉,張 亮,王 聰,等.基于Logvinovich獨立膨脹原理的超空泡形態計算方法[J].兵工學報,2009,30(3):361-365. Zhang Xuewei,Zhang Liang,Wang Cong,et al.A calculation method for supercavity shape based on the Logvinovich Independence Principle of the cavity section expansion[J].Acta Armamentarii,2009,30(3):361-365.

[13]權曉波,李 巖,魏海鵬,等.航行體出水過程空泡潰滅特性研究[J].船舶力學,2008,12(4):545-549. Qüan Xiaobo,Li Yan,Wei Haipeng,et al.Cavitation collapse characteristic research in the out-of-water progress of underwater vehicles[J].Journal of Ship Mechanics,2008,12(4):545-549.

[14]王獻孚.空化泡和超空化泡流動理論及應用[M].北京:國防工業出版社,2009. Wang Xianfu.Cavitating and supercavitating flows theory and applications[M].Beijing:Defense Industry Press,2009.

Three-dimensional cavitation shape of the underwater vehicles at a small attack angle in unsteady flow

CHENG Shao-hua,QUAN Qiao-bo,YU Hai-tao,ZHAI Zhang-ming,WANG Zhan-ying
(Beijing Institute of Astronautical System Engineering,Beijing 100076,China)

Asymmetry of unsteady cavities can be formed when the body moves with a high speed and small attack angle,which is the main design basis of hydrodynamics and hydroballistics.Theoretical model is established based on Logvinovich independence principle,considering the influence of crossflow effect.A typical case is simulated to get cavity length of the face flow surface and the back flow surface,as well as cavity pressure.Finally,the comparison is performed between the results of the theoretical model and the experiment,which confirms the theoretical approach in this study.

cavity shape;partially cavitation;Logvinovich independence principle;hydrodynamics;unsteady

O352

A

10.3969/j.issn.1007-7294.2015.08.001

1007-7294（2015）08-0889-07

2015-03-23

國防基礎科研項目（A0320110015）和973項目（613171）

程少華（1982-），男，工程師，E-mail:chengshaohua_2008@163.com；權曉波（1976-），男，博士后。