考慮應變強化效應海底管道極限承載力研究

陳嚴飛，張娟，張宏，蔡峰峰

（1中國石油大學（北京）油氣管道輸送安全國家工程實驗室/城市油氣輸配技術北京市重點實驗室，北京102249；2中國電建集團北京勘測設計研究院，北京100024；3石油工程設計有限責任公司北京分公司，北京100085）

考慮應變強化效應海底管道極限承載力研究

陳嚴飛1，張娟2，張宏1，蔡峰峰3

（1中國石油大學（北京）油氣管道輸送安全國家工程實驗室/城市油氣輸配技術北京市重點實驗室，北京102249；2中國電建集團北京勘測設計研究院，北京100024；3石油工程設計有限責任公司北京分公司，北京100085）

文章基于線性強化材料模型，推導了軸向拉力作用下海底管道極限彎矩承載力解析解，給出了海底管道在軸向拉力與彎矩載荷同時作用下的極限承載力的近似解，編制了海底管道極限承載力計算程序BCP。通過與實驗結果的比對，驗證了解析方法的正確性。結論表明考慮應變強化效應的海底管道極限承載力結算結果更為合理，該文可為海底管道的結構強度設計和安全性評價提供一定的參考依據。

海底管道；極限彎矩承載力；應變強化

0 引言

海底管道在海洋油氣田開發中有著至關重要的作用。近年來我國海洋油氣資源的大量開發極大地促進了海底管道的建設。海底管道常用的鋪設方法為S形和J形，為了防止管道在靜水外壓作用下發生壓潰，可以采用充水鋪設的方法，相比空管鋪設；管道中軸向拉力會明顯增加，此時管道的上彎段和下彎段都會受到較大軸向拉力和彎曲荷載的聯合作用，如圖1所示[1]。此外，在運行期間，管道受到各種海底復雜載荷的作用，包括地震，滑坡等。這些復雜作用情況下，彎曲荷載也可能是引起管道破壞的關鍵荷載。因此，確定管道的極限彎矩承載力對海底管道的結構強度設計和安全評價都至關重要。

圖1 海底管道鋪設S形和J形鋪設示意圖Fig.1 Schematics of S-lay and J-lay for offshore pipelines

從上世紀70年代開始，管道極限彎矩承載力便成為了國內外學者關注的對象。Bouwkamp等[2]、Sherman等[3]進行了全尺寸的實驗方法研究，得到了管道在彎矩荷載下的承載和變形能力，也得到了一些重要的結論，給管道的設計提供了一定的參考[2]。Karamanos等[4-5]采用實驗和數值方法對管道在彎矩荷載作用下的失效模式做了進一步的研究，并得出一些重要結論。Bai等[6]、Mohareb等[7-8]基于理想彈塑性假設和mises屈服準則，推導了內壓與軸向力共同作用下管道的極限彎矩載荷的解析解。通過與實驗數據的對比，該解析解能很好預測管道極限彎矩載荷。該研究部分成果被DNV-OS-F101采用。

在國際管道研究協會的贊助（PRCI）下，Gresnig等[9-10]通過實驗方法研究了管道制作方式對極限彎矩荷載的影響，實驗中采用管道的徑厚比分別為22、27、29、45，表明管道的制作方式會影響管材的Bausching效應，從而影響管道的承載力，而且管道的應變強化效應對管道的極限彎矩承載力也有較大的影響。Schaumann等[11]采用四點彎實驗和有限元方法研究了管道在內壓和彎矩荷載作用下的極限承載力，并基于梁的微分方程推導了管道在內壓荷載和彎矩荷載聯合作用下的解析解。Corona等[12]，Kyriakides等[13]使用實驗的方法得到了管材各向異性對管道極限承載力的影響。國內學者賈旭等[14]、曹靜等[15]、陳嚴飛等[16]、龔順風等[17]、任慧龍等[18]、余建星等[19]針對海底管道的結構強度問題開展了大量的研究，得出了一些可供工程參考的結論。

目前大多研究是基于理想彈塑性模型假設開展的，沒有考慮應變強化效應的影響。本文采用線性強化模型，推導得到了海底管道在軸向拉力與彎矩載荷共同作用下的極限承載力解析解，為了簡化計算過程，給出了管道極限彎矩承載力簡化解析解，并通過試驗結果驗證了結果的合理性，為海底管道結構強度設計和安全評價提供了一定的參考。

1 基本理論

對于線性強化材料，在彈性階段應力應變關系可以表示為：

在應變強化階段應力應變關系可以表示為：

其中：α為線性強化系數，α=E1/E，E和E1通常可以通過管材試驗數據擬合得到。圖2為X52和X56鋼的應力應變實測值與擬合的線性強化曲線。

圖2 X52和X56鋼線性強化應力應變關系Fig.2 Elastic-linear strain hardening for X52 and X56 pipe steel

忽略材料的壓縮變形，在彈性階段

在應變強化階段

其中：σe為有效應力，εe為有效應變。

Henchy全量理論可以表示為：

其中：ez，eθ，er為軸向、環向和徑向的應變偏張量，sz，sθ，sr為相應的應力偏張量。

2 理想彈塑性管道極限彎矩承載力解析解

采用理想彈塑性模型，管道在軸向拉力和彎矩荷載作用下，達到塑性極限狀態后，管道截面的應力分布如圖4所示。

圖3 管道橫截面應力分布圖Fig.3 Stress distribution on pipe cross section

在確定塑性極限彎矩荷載之前，首先需要決定塑性中性軸的位置。首先對管道截面進行積分，可以得到管道的軸向拉力為：

進而可以得到塑性中性軸夾角ψ，

如圖3所示的管道在極限狀態時的應力分布，管道的極限彎矩可以表示為

3 線性強化管道極限彎矩承載力解析解

管道在彎矩與軸向力的綜合作用下，存在三個階段：線彈性階段，初次強化階段，二次強化階段。管道三個階段在截面上的應力分布如圖4所示。其中灰色區域為彈性區域，黑色區域為塑性區域。在線彈性階段，管道截面均處于彈性階段；當管道任意一側最外層進入塑性后，管道進入初次強化階段，此時管道截面上一部分處于彈性階段，另一部分處于塑性階段。當管道兩側均進入塑性階段后，管道進入二次強化階段。此時，管道只在中心區域處于彈性階段。隨著載荷的增加，塑性區域向中心區域擴展，使得彈性區減小，直到管道破壞。

圖4 應變強化管道截面應力分布圖Fig.4 Stress distribution on pipe cross section considering strain hardening effect

根據平截面假定，管道截面的應變為線性分布，可以表示為：

其中：ψ為管道中性軸夾角，ω為曲率。

在彈性區域，管道軸向應力可以表示：

在塑性區域，根據Henchy全量理論，忽略管材的壓縮變形，，此時，管道的軸向應力可以表示為：

第一階段：線彈性階段，在此階段管道的軸向拉力為：

由上式可以確定中性軸的位置，也就是ψ值為：

確定中性軸的位置后，可以確定管道的彎矩荷載為：

第二階段：初次強化階段，在此階段管道的軸向拉力可以表示為

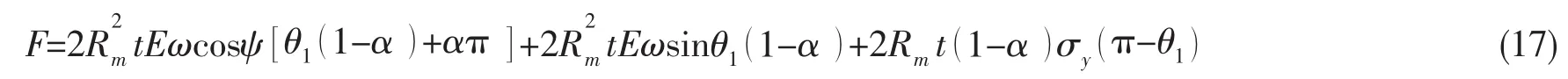
在管道截面θ1位置，為彈性區域和塑性區域的交界面，此時管道的應變滿足：

聯合求解（17）式和（18）式可以確定ψ和θ1，管道的彎矩荷載可以表示為：

第三階段：二次強化階段，管道的軸向拉力可以表示為：

在彈性和塑性區域的交接區域：

聯立（20）、（21）式和（22）式，可以求得ψ、θ1和θ2，管道的彎矩荷載可以表示為：

可以看出，管道的彎矩荷載與曲率密切相關，隨曲率的增加管道截面上的應力逐漸增加，管道彎矩荷載也會逐漸增加，當曲率達到一定值時，管道截面上的最大應力達到σmax，σmax通常可以取值為管材的極限抗拉強度σu，管道發生破壞，此時對應的彎矩荷載即為管道極限彎矩荷載。

4 考慮應變強化效應管道極限彎矩承載力簡化解析解

采用線性強化模型，首先需要通過管材的應力應變關系來擬合得到管材強化參數，然后分析管道的整個彈塑性變形過程，得到管道的極限彎矩荷載，計算過程較為繁瑣。為了簡化計算過程，本文提出了一種簡化計算方法，更加適合工程應用。在軸向拉力和彎矩荷載的聯合作用下，管道進入極限狀態，截面應力分布如圖5所示，當管道一側纖維應力達到σmax，管道就會發生破壞，此時管道所承受彎矩荷載即為極限彎矩荷載。

根據圖5的管道截面上的應力分布，管道的軸向拉力可以表示為

圖6 G（ψ）示意圖Fig.6 G（ψ）versus ψ

根據方程（25）可以迭代求出ψ，為了便于工程應用，可以采用如下近似計算方法，首先定義函數G（ψ）為：

對于管道受到軸向拉力作用的情況，0≤ψ≤π/2，采用最小二乘法進行擬合，G（ψ）可以簡化成為一個二次多項式：

其中：k0=0.482，k1=0.121，k2=-0.259。

由圖6可以看出，方程（26）計算值與方程（27）擬合值吻合很好。

將（26）式代入到（25）式，得到

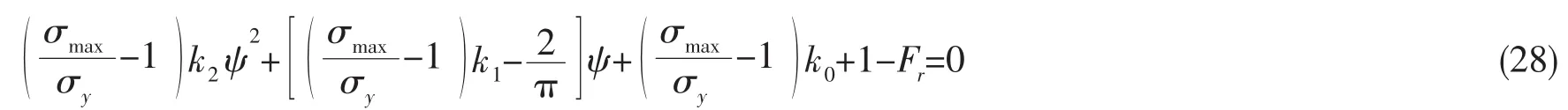
解上述二次方程，可以求得ψ，確定中性軸的位置。

管道極限彎矩荷載可以表示為：

當管道僅受彎矩荷載作用，此時ψ=π/2，管道的極限彎矩荷載可以簡化為：

通常σmax可以取值為管材的極限抗拉強度σu，因此已知管道的幾何參數，管材屈服強度σy和極限抗拉強度σu，即可計算管道的極限彎矩荷載。

針對上文給出的管道極限彎矩承載力理想彈塑性模型解析解、線性強化模型解析解和簡化解析解，本文編制了管道在軸向拉力作用下的極限承載力計算程序BCP。

5 實驗驗證

為了驗證管道在軸向拉力作用下極限彎矩承載力的彈塑性模型解析解、線性強化模型解析解和簡化解析解計算結果的精確程度，本文采用荷蘭代爾夫特理工大學Gresnigt[9-10]等開展的管道極限彎矩承載力相關試驗數據結果來進行驗證，試驗管道具體參數如表1所示。

圖7為管道極限彎矩載荷的理論計算結果與實驗結果的對比。橫坐標為試驗工況編號，縱坐標為理論計算值與實驗值的比值。理論計算采用了理想彈塑性模型與線性強化模型解析解，線性強化模型簡化解析解。

圖7 實驗結果與計算結果對比圖Fig.7 Comparison of measured and estimated bending capacity

表1 管道實驗參數Tab.1 Parameter for pipeline specimens

由圖7可以看出，現有規范中采用理想彈塑性模型計算管道極限抗彎承載力偏于保守，考慮應變強化的管道極限彎矩承載力與實驗值吻合更好，線性強化管道極限抗彎承載力簡化解析解和解析解的結果非常接近，表明采用近似解析方法即可較為準確計算管道極限彎矩承載力，并可以考慮管材應變強化效應。

6 結論

海底管道鋪設安裝和運行過程中，彎矩荷載可能成為引起管道破壞的關鍵荷載，確定海底管道的極限彎矩承載力具重要的工程意義。本文采用線性強化模型，推導得到了管道在軸向拉力作用下的極限彎矩承載力的解析解，給出了簡單解析解，并得到了實驗數據的驗證。得到的重要結論如下：當管道進入全塑性狀態后，管材的應變強化會起到重要的作用。這種情況下的管材若使用理想彈性模型會導致預測值偏于保守，可以作為管道極限彎矩載荷的下限值。而采用應變強化材料時，可以更好地預測管道的彎矩荷載。本文給出了海底管道極限彎矩承載力計算方法，可以為海底管道的強度設計和安全性評價提供一定的參考。

[1]Kyriakides S,Corona E.Mechanics of offshore pipelines[M].Elsevier,2007.

[2]Bouwkamp J G,Stephen R M.Structural behaviour of large diameter pipe under combined loading[J].Journal of Transportation Engineering,1973,99(TE3):521-536.

[3]Sherman D R.Test of circular steel tubes in bending[J].Journal of the Structural Division,ASCE,1976,102(ST11): 2181-2195.

[4]Karamanos S A,Tassoulas J L.Tubular members I:Stability analysis and preliminary results[J].Journal of Engineering Mechanics,ASCE,1996,122(1):64-71.

[5]Karamanos S A,Tassoulas J L.Tubular members II:Local buckling and experimental verification[J].Journal of Engineering Mechanics,ASCE,1996,122(1):72-78.

[6]Bai Y,Igland R T,Moan T.Ultimate limit state of pipes under tension and bending[J].International Journal of Offshore and Polar Engineering,1994,4(4):312-319.

[7]Mohareb M,Kulak G L,Murray D W.Testing and analysis of steel pipe section[J].Journal of Transportation Engineering, 2001,127(5):408-417.

[8]Mohareb M.Plastic interaction relations for pipe sections[J].Journal of Engineering Mechanics,2002,128(1):112-120.

[9]Gresnigt A M,van Foeken R J.Local bucking of UOE and seamless steel pipe[C]//11th International Offshore and Polar Engineering Conference.Stavanger,Norway,2001,2:131-142.

[10]Gresnigt A M,Karamanos S A,Andreakadis K P.Lateral loading of internally pressurized steel pipes[J].Journal of Pressure Vessel Technology,ASME,2007,129:630-638.

[11]Schaumann P,Keindorf C,Bruggemann H.Elasto-plastic behavior and buckling analysis of steel pipelines exposed to internal pressure and additional loads[C]//International Conference on Offshore Mechanics and Arctic Engineering,OMAE.Halkidiki,Greece,2005:597-607.

[12]Corona E,Lee L H,Kyriakides S,Yield anisotropy effects on buckling of circular tube under bending[J].International Journal of Solids and Structures,2006,43(22-23):7099-7118.

[13]Kyriakides S Ok A,Corona E.Localization and propagation of curvature under pure bending in steel tubes with Lüders bands[J].International Journal of Solids and Structures,2008,45(10):3074-3087.

[14]賈旭,侯靜,田英輝.靜水壓力作用下海底單層保溫管道壓潰屈曲分析[J].中國海上油氣,2006(10),18(5):341-352. Jia Xu,Hou Jing,Tian Yinghui.The buckling analysis on single layer insulation pipeline acting by external hydrostatic pressure[J].China Offshore Oil and Gas,2006(10),18(5):341-352.(in Chinese)

[15]曹靜,王章嶺,田英輝,等.單重保溫海底管線鋪設過程中的壓潰分析[J].中國造船,2006,47(增):351-358. Cao Jing,Wang Zhangling,Tian Yinghui,et al.Crushing analysis during single insulation pipeline laying[J].China Shipbuilding,2006,47(Special):351-358.(in Chinese)

[16]陳嚴飛,李昕,周晶.不規則腐蝕缺陷管道極限承載力研究[J].工程力學,2009,26(11):190-196. Chen Yanfei,Li Xin,Zhou Jing.Ultimate bending capacity of pipe with arbitrary corrosion defects[J].Engineering Mechanics,2009,22(2):43-49.(in Chinese)

[17]龔順風,陳源,金偉良,等.高靜水壓力作用下深海油氣管道的局部屈曲[J].浙江大學學報（工學版）,2009,46(1): 14-19. Gong Shunfeng,Chen Yuan,Jin Weiliang,et al.Local buckling of deepwater oil-gas pipeline under high hydrostatic pressure[J].Journal of Zhejiang University(Engineering Science),2009,46(1):14-19.(in Chinese)

[18]任慧龍,李陳峰,夏雪.腐蝕海底管道剩余強度的可靠性評估方法研究[J].船海工程,2009,38(5):124-128. Ren Huilong,Li Chenfeng,Xia Xue.Reliability assessment method for residual strength of corroded pipeline[J].Ship& Ocean Engineering,2009,38(5):124-128.(in Chinese)

[19]余建星,卞學航,余楊,等.深海海底管道全尺寸壓潰試驗及數值模擬[J].天津大學學報（自然學科版）,2012,45 (2):154-159. Yu JianXing Bian Xuehang Yu yang.Full-Scale collapse test and numerical simulation of deepwater pipeline[J].Journal of Tianjin University(Science and Technology),2012,45(2):154-159.(in Chinese)

Ultimate bending capacity of offshore pipeline considering strain hardening effect

CHEN Yan-fei1,ZHANG Juan2,ZHANG Hong1,CAI Feng-feng3
(1 National Engineering Laboratory for Pipeline Safety/Beijing Key Laboratory of Urban Oil and Gas Distribution Technology,China University of Petroleum,Beijing 102249,China;2 Powerchina Beijing Engineering Corporation Limited,Beijing 100024,China;3 China Petroleum Engineering Co.,Ltd.,Beijing Company,Beijing 100085,China)

Based on Hencky’s total strain theory of plasticity,ultimate bending capacity of offshore pipeline can be determined analytically assuming linear strain hardening material.The methods proposed in this paper are able to account for the combined action of internal pressure and axial tensile force.Good accuracy is observed when ultimate bending capacities obtained from analytical solutions are compared with experimental results from full-size tests of steel pipes.The results show that the elastic-perfectly plastic material used comely yield lower than the strain hardening material pipes,and may underestimate the ultimate bending capacity of the pipes.The solutions proposed in this paper are applicable in the structural design and safety evaluation of offshore pipelines.

offshore pipelines;ultimate bending capacity;strain hardening

TE973

A

10.3969/j.issn.1007-7294.2015.04.010

1007-7294（2015）04-0420-08

2014-12-23

國家自然科學基金（51309236）；教育部博士點基金（20120007120009）；上海交通大學海洋工程國家重點實驗室開放基金（1314）；天津大學水利工程仿真與安全國家重點實驗室開放基金（HESS-1411）

陳嚴飛（1982-），男，博士后，Email:ychen@cup.edu.cn；張娟（1982-），女，高級工程師。