兩種運動平臺下晃蕩沖擊荷載的實驗研究

衛志軍，陳曉東，董玉山，唐 彬，岳前進（大連理工大學 工業裝備結構分析國家重點實驗室，遼寧 大連116023）

兩種運動平臺下晃蕩沖擊荷載的實驗研究

衛志軍，陳曉東，董玉山，唐 彬，岳前進
（大連理工大學 工業裝備結構分析國家重點實驗室，遼寧 大連116023）

由液體晃蕩引起的沖擊荷載主要與外部激勵(激勵頻率和激勵幅值)和裝載率相關。大尺度物理模型實驗通過運動平臺在室內復現液艙的運動，進而實現在室內對儲液艙內晃蕩載荷的研究。因此，平臺的運動能力、運動的精確性對液體沖擊載荷的實驗結果非常關鍵。為了研究不同類型運動平臺的運動性能及其對儲液艙內沖擊載荷的影響，文中以大比尺二維矩形艙為模型，分別在單自由度運動平臺和六自由度運動平臺開展系統的液體晃蕩沖擊實驗。實驗結果表明：僅考慮水平運動，單自由度平臺的精度要高于六自由度平臺；在個別工況下，兩個平臺下沖擊荷載時程和特征值的對比結果出現了一定差別，但是晃蕩沖擊荷載的整體趨勢基本一致。通過評價單自由度和六自由度兩種類型的運動平臺在液體晃蕩研究領域應用的適用性，為大尺度室內晃蕩模型實驗中運動平臺的選擇提供參考

大尺度物理子模型實驗；平臺運動性能；沖擊荷載；對比研究

0 引 言

新型浮式液化天然氣儲卸裝備Floating Liquefied Natural Gas（FLNG），可實現對深、遠海油氣的開采、液化、儲存與裝卸。該新型超大型浮式運載裝備需要超大容積的儲液艙[1]。儲艙正在向超大型化發展，液體發生晃蕩引起的砰擊問題更加顯著[12]。砰擊載荷不僅會影響運載裝備的運動姿態，也會直接威脅儲罐的結構安全。因此砰擊載荷是艙壁加強結構設計中的控制荷載。

液體砰擊艙壁時產生的物理現象非常復雜[2-4]，使得線性理論和非線性理論對大振幅激勵下晃蕩沖擊載荷的預測均存在一定的局限性[3，5]，而基于這些理論開展的數值實驗也未能充分地考慮真實的物理現象，因而也難以用來解釋晃蕩沖擊載荷[3，5-7]。室內液體晃蕩模型實驗能較真實地反映液艙內液體晃蕩的復雜物理現象，因此可用為研究晃蕩載荷的重要方法[5，8-9]。

國內外各晃蕩研究機構均采用運動平臺在室內復現液艙的運動。運動平臺的運動性能直接影響晃蕩載荷的實驗結果。美國船級社提出室內運動平臺首先需要在保證系統誤差范圍內模擬最危險的船體運動。此外，平臺的工作臺面至少能夠實現1：50比尺的模型試驗[1]。國外晃蕩研究機構多采用六自由度運動平臺，承載能力一般是1噸或4噸[10]。國內晃蕩研究機構普遍采用單自由度運動臺和多自由度運動臺。陳穗康等人[11]利用曲柄連桿機構推動平臺繞軸作定角度簡諧運動，實現了液艙縱搖單自由度模擬。衛志軍等人[6]借助油壓作動器分別實現單自由度平動和單自由度轉動的模擬。王德禹等人[12]采用的三自由度液艙晃蕩模擬裝置實現橫搖、縱搖和升沉三個自由度的運動模擬。近年來，六自由度運動平臺在國內液體晃蕩研究領域得到了較廣泛的應用。中國船舶科學研究中心液艙晃蕩模擬機構采用4噸的六自由度運動平臺開展了一系列的液體晃蕩實驗研究[13]。衛志軍等人[14]利用12噸的六自由度運動平臺開展大尺度儲艙液體晃蕩砰擊壓力測量方法研究。然而，尚未有研究闡述單自由度和六自由度運動平臺的適用特點和其在液體晃蕩研究領域應用的局限性。

除此之外，晃蕩載荷對外激激勵（激勵頻率和激勵振幅）和載液高度非常敏感[6，15-16]。但由于運動平臺和模型實驗的成本較高，針對晃蕩載荷對外激激勵敏感性的分析較少。衛志軍等[6]以三維矩形液艙為研究模型，在單自由度平臺上僅針對高載液率分析晃蕩載荷對外激激勵的敏感性。然而，在LNG穿梭船的航運過程中，由于液體晃蕩產生的水動力載荷引起液艙艙壁破壞的事故均發生在低載液工況[17]。因此針對中、低載液下，晃蕩載荷對外激激勵的敏感性的研究具有工程意義。而國內外針對晃蕩沖擊荷載對外激激勵的敏感性研究尚不完善。為此，本文設計并分別采用單自由度和六自由度兩種類型的運動平臺，對大比尺的二維矩形液艙中低、中載液率下液體晃蕩引起的砰擊載荷進行了實驗觀測和研究。采用相同的簡諧橫蕩激勵模型、傳感器布點位置、載液水平及數據采集方式對砰擊載荷進行測量。通過對比分析液體砰擊的物理現象及沖擊壓力的特征值與外激激勵頻率和幅值的關系，評價單自由度和六自由度兩種類型的運動平臺在液體晃蕩研究領域應用的適用性，為大尺度室內晃蕩模型實驗中運動平臺的選擇提供參考。

1 晃蕩模型實驗

1.1 實驗裝置及方法

晃蕩室內模型實驗在大連理工大學工業裝備結構分析國家重點實驗室內開展。實驗的設備主要包括單自由度運動平臺、六自由度運動平臺、二維矩形液艙、位移和壓力傳感器以及數據和圖像采集系統。實驗系統如圖1所示，其中（a）單自由度運動平臺（Translational platform），（b）六自由度運動平臺（Hexapod test rig），（c）平臺控制系統（Platform control system），（d）平臺運動采集系統（Rig motions acquisition），（e）壓力傳感器（Pressure sensors），（f）圖像采集系統（Image acquisition）。

單自由度運動平臺（Translational platform），圖1（a）所示，可模擬船舶的橫蕩或縱蕩運動，其承重能力為10 ton，最大位移行程為±150 mm，運動精度為±0.5 mm[6]；六自由度運動平臺（Hexapod test rig），如圖1（b）所示，可模擬船體單個自由度或多個自由度耦合的規則和不規則運動，平臺承重能力為12 ton，平動最大位移行程為±800 mm，靜態誤差±1 mm，轉動最大角度行程為±28°，靜態誤差±0.1°，經調研該大噸位六自由度平臺的承載和運動性能均達到國際領先[14]。單自由度和六自由度平臺的運動控制系統分別如圖1（c1）和（c2）所示。

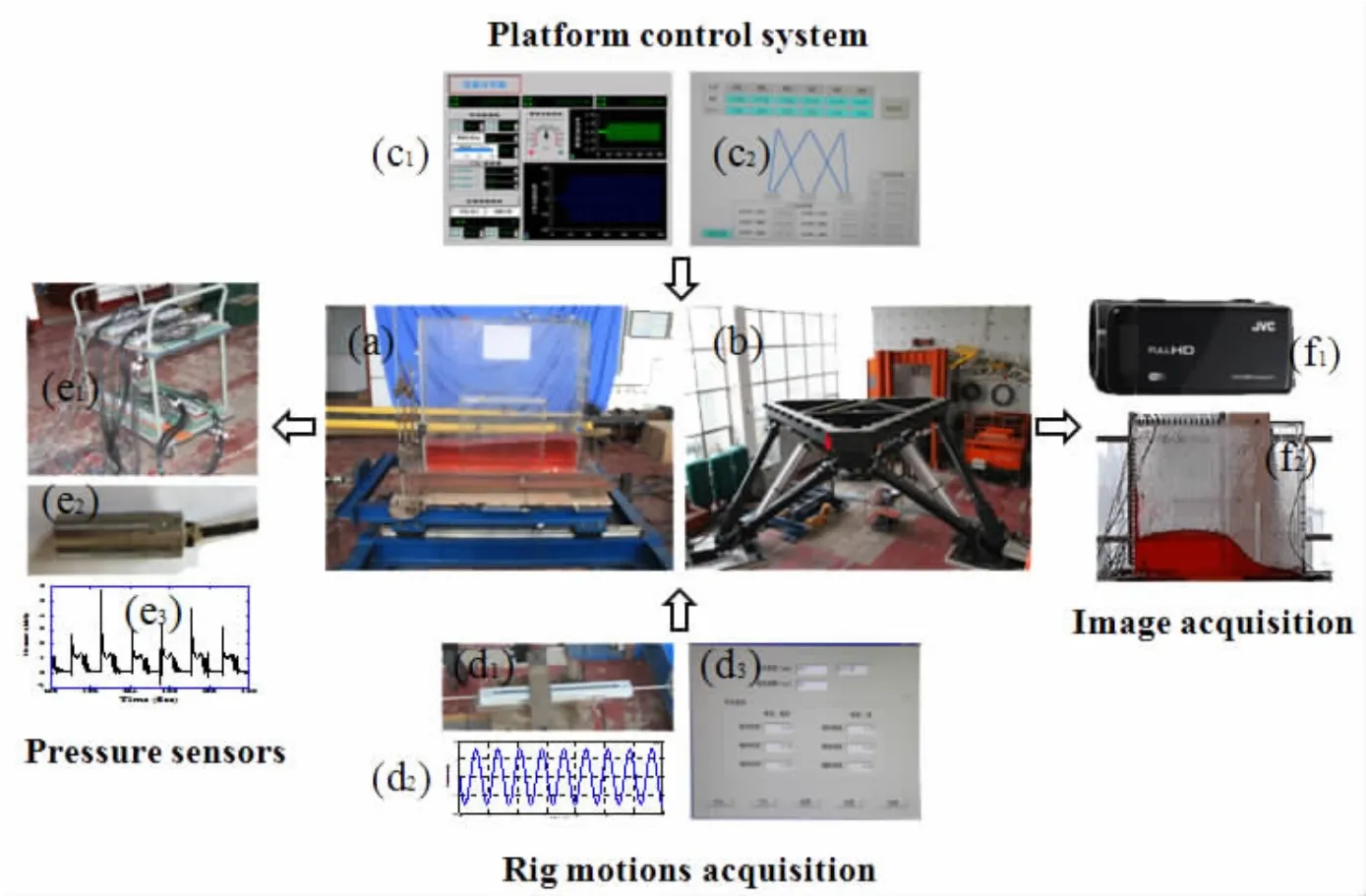
圖1 晃蕩模型實驗系統Fig.1 Sloshing model test system

兩次實驗采用相同的橫蕩規則激勵，平臺運動位移公式為：

式中：A為平臺運動幅值，f為激勵頻率，t為運動時間。

實驗過程中實時采集兩個平臺運動位移。其中，利用位移傳感器，圖1（d1）所示，對單自由度平臺運動進行監測，圖1（d2）為單自由度平臺實時的位移時程；對于六自由度運動平臺，可以利用控制程序實時輸出位移時程，如圖1（d3）所示。

二維矩形艙內壁長為970 mm（L），寬為158 mm（B）和高為927 mm（H）。選取h/H=0.2和h/H=0.6作為實驗對比研究的載液率（h為載液高度），相較于h/H=0.6載液率，在低載液率h/H=0.2時，流體自由液面的非線性更強，物理現象更加復雜。實驗采用的壓力傳感器，圖1（e1和e2）所示，其感應區域是直徑為10 mm的圓形，量程為50 kPa，精度為滿量程的0.48%[10]。對于不同的載液率，艙內流體晃蕩時對艙壁的沖擊位置主要集中于其對應的靜水面附近。因此，兩個載液率的實驗研究所關注的傳感器位置不同。h/H=0.2載液率實驗主要關注Sensor1、Sensor2和Sensor3的采集數據；而h/H=0.6載液率實驗主要關注Sensor5、Sensor6和Sensor7的采集數據。二維矩形液艙主尺度及壓力傳感器布局方案如圖2所示。本文采用高速攝像機對艙內流體晃蕩過程中的自由液面波形變化及不同的物理現象進行記錄，如圖1（f1和f2）。

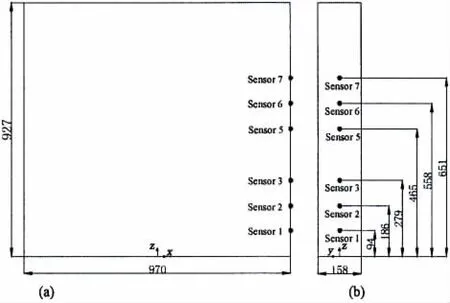
圖2 液艙主尺度及傳感器布置（mm）：（a）正視圖；（b）側視圖Fig.2 Tank geometry and sensor configuration(mm): (a)Front view;(b)Side view

1.2 模型實驗工況

通過邊界條件、線性自由液面運動和動力條件求解二維Laplace控制方程，得到二維矩形液艙自由液面的固有頻率計算公式：

式中：g為重力加速度，h為載液高度，L為液艙的長度，n為階數，ωn為自由液面固有圓頻率。fn=ωn/ 2π，fn為自由液面的固有頻率。

當外激頻率接近自由液面最低階固有頻率ω1時，艙內液體晃蕩最劇烈。1965年，Verhagen和van Wijngaarden推導出二維矩形艙淺水工況下，流體晃蕩過程中發生水躍的外激頻率的范圍，其計算公式如下：

式中：ω為理論計算水躍發生對應的自由液面圓頻率。由上述兩式可以計算載液率h/H=0.2和h/H= 0.6的自由液面最低階固有頻率及淺水工況（載液率h/H=0.2）下流體可能發生水躍的頻率范圍為f/f1∈（0.726，1.274）。

實驗具體工況設計如下：當h/H=0.2，在理論計算的發生水躍的外激頻率范圍內，開展一系列掃頻實驗。該液位對應的橫蕩激勵幅值為A=30 mm，激勵頻率變化范圍是0.7 f1到1.3 f1，對應的最低階頻率為f1=0.660 Hz；對于h/H=0.6，針對激勵振幅開展一系列實驗，激勵頻率為液面的最低階固有頻率f1=0.875 Hz，橫蕩激勵幅值A分別為20 mm，30 mm，40 mm和50 mm，具體實驗工況如表1所示。

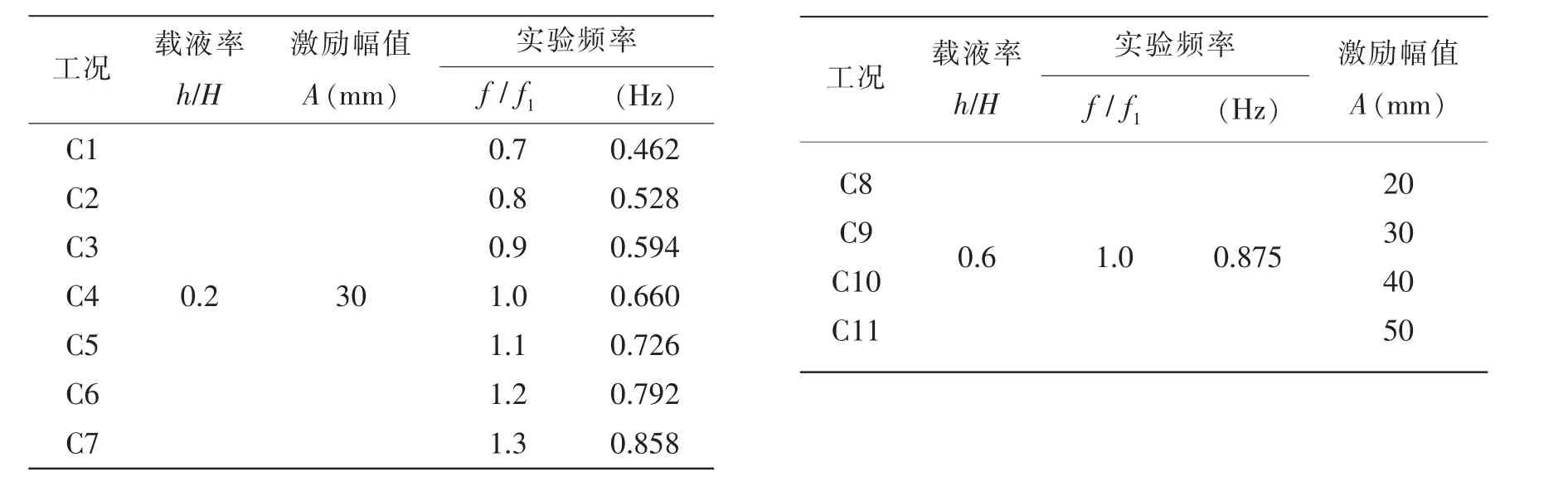
表1 實驗工況：（a）載液率h/H=0.2；（b）載液率h/H=0.6Tab.1 Experimental conditions：(a)h/H=0.2;(b)h/H=0.6 （a） （b）

2 平臺運動性能對比分析

本文定義六自由度平臺沿液艙x、y和z軸方向的平動分別為橫蕩、縱蕩和垂蕩，而繞液艙x、y和 z軸方向的轉動分別為縱搖、橫搖和艏搖。圖3分別給出了C1和C10工況下，單自由度和六自由度運動平臺一段典型的位移時程曲線。從圖3可以看出，六自由度平臺的實際運動幅值大于單自由度平臺的運動幅值；兩個平臺的實際位移均略大于平臺輸入位移，但是單自由度的運動精度更高一些。作者認為造成六自由度平臺實際運動幅值略大于輸入幅值的原因是：六自由度平臺在實現單個自由度的運動時，其他五個自由度會在合理誤差范圍內發生微小的運動（詳見表2）。而單自由度平臺運動不受此影響，因此其能夠較準確地實現單個自由度的運動。盡管如此，平臺的運動輸出均在合理的實驗系統誤差范圍內。針對每個實驗工況，計算平臺運動實時輸出位移的誤差均值為：單自由度平臺0.8%和六自由度平臺2.1%，均在合理的實驗系統誤差范圍內。建議應根據每次實驗的具體情況分析平臺的系統誤差。

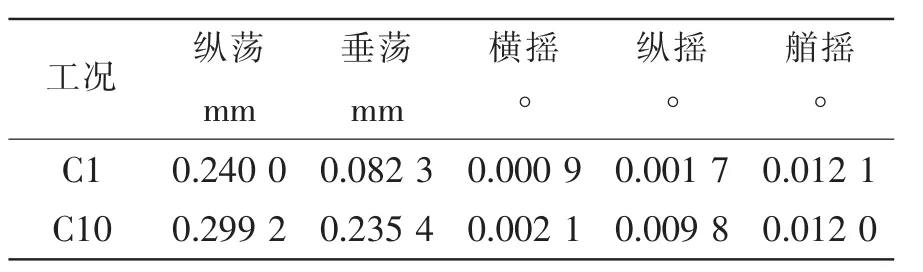
表2 工況C1和C10，六自由度平臺實際運動Tab.2 Actual motions of hexapod test rig of C1 and C10

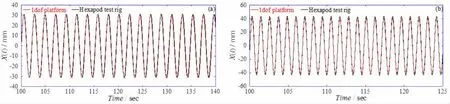
圖3 單自由度和六自由度平臺運動位移時程：（a）工況C1；（b）工況C10Fig.3 Time history of 1dof platform and hexapod test rig actual motions:(a)C1;(b)C2

3 晃蕩沖擊荷載對比分析

本節主要從晃蕩沖擊載荷的角度，研究單自由度平臺和六自由度平臺對其的影響。首先從晃蕩沖擊載荷的時程曲線對比。然后，討論在低載液工況下（h/H=0.2），晃蕩沖擊荷載的特征壓力值隨外激頻率的變化關系。最后，研究在中載液工況下（h/H=0.6），晃蕩沖擊荷載的特征壓力值隨外激幅值的變化關系。

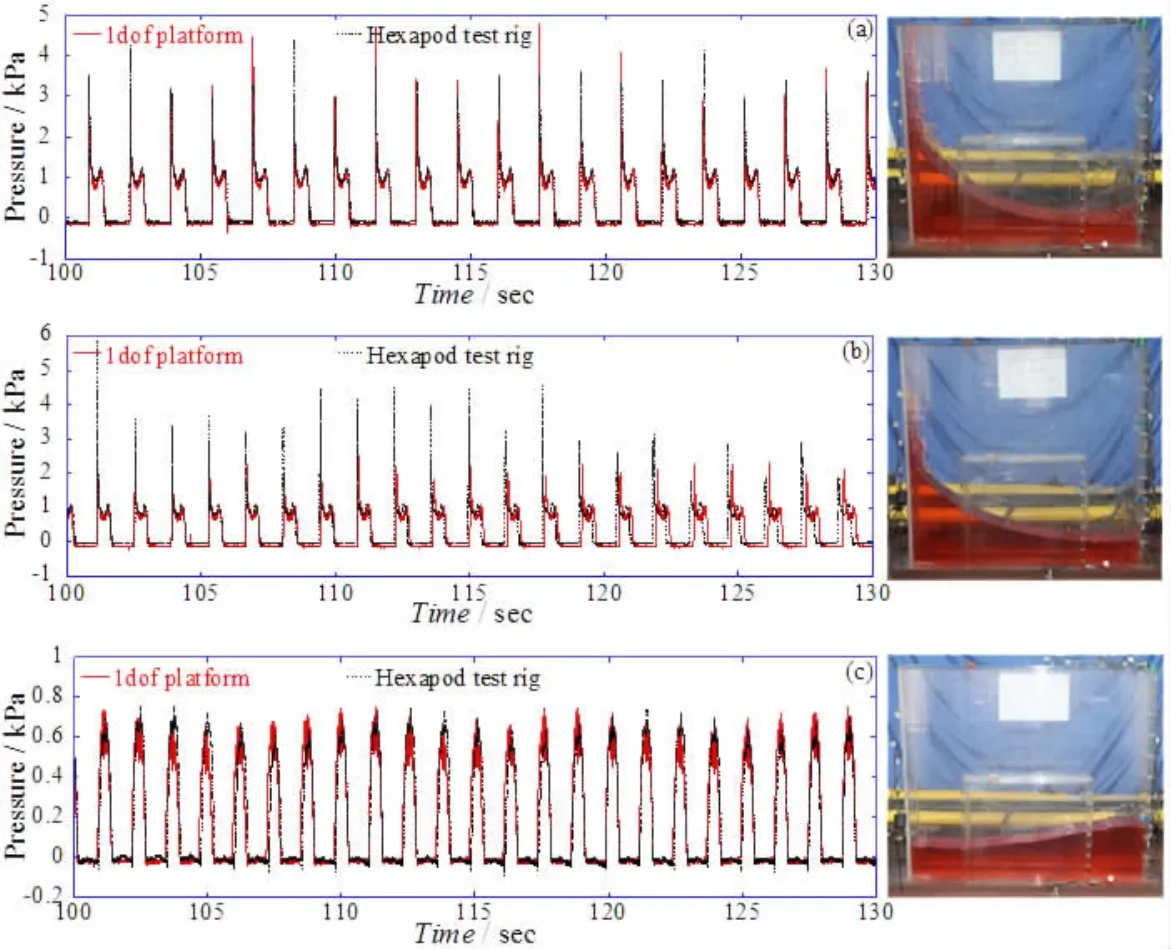
圖4 Sensor2壓力時程曲線對比：（a）C4；（b）C5；（c）C6Fig.4 Pressure time histories of Sensor2:(a)C4;(b)C5;(c)C6

3.1 沖擊荷載時程曲線對比

圖4分別給出了h/H=0.2載液率，激勵幅值A=30 mm，實驗頻率f/f1=1.0、1.1和1.2時，兩次實驗中靜水面處傳感器Sensor2的壓力時程曲線。從圖中可以看出，即使是完全相同的兩個實驗工況，兩個平臺的實驗結果也很難達到完全一致，一是每一個沖擊壓力峰值在兩次實驗中不可能都完全同時發生，二是即使同時發生沖擊作用，其峰值也不能完全相同，這種差異在f/f1=1.1時更加顯著（圖4（b）），但是晃蕩沖擊壓力的形式是基本保持一致的。GTT公司的研究人員在不同的運動平臺也發現了這一差異性[10]。圖4（a）和（b）的兩組實驗都發生了明顯的晃蕩沖擊作用，每次沖擊呈現雙峰值，第一個峰值是液體晃蕩產生的沖擊性的水動壓力，第二個峰值是由于液體的慣性力產生的非沖擊性壓力。此外，由于實驗頻率遠離自由液面最低階固有頻率，實驗中并無明顯的沖擊現象，因此f/f1=1.2工況下，壓力時程曲線表現出非沖擊性（圖4（c））。

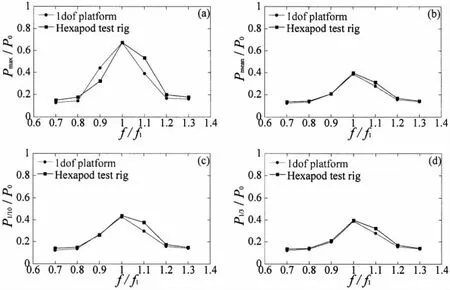
圖5 晃蕩沖擊荷載隨外激頻率的變化關系，h/H=0.2載液率，Sensor1：（a）Pmax；（b）Pmean；（c）P1/10；（d）P1/3，P0=ρgLFig.5 The relationship between sloshing impact loads and oscillation frequency,h/H=0.2 filling level,Sensor1: (a)Pmax;(b)Pmean;(c)P1/10;(d)P1/3,P0=ρgL

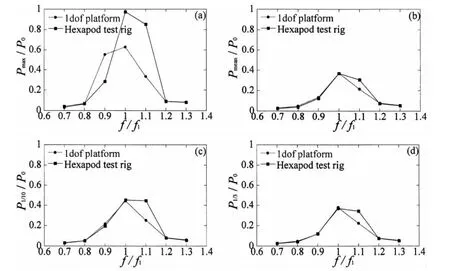
圖6 晃蕩沖擊荷載隨外激頻率的變化關系，h/H=0.2載液率，Sensor2：（a）Pmax；（b）Pmean；（c）P1/10；（d）P1/3，P0=ρgLFig.6 The relationship between sloshing impact loads and oscillation frequency,h/H=0.2 filling level,Sensor2: (a)Pmax;(b)Pmean;(c)P1/10;(d)P1/3,P0=ρgL

3.2 晃蕩沖擊荷載與外激頻率的關系

在低載液工況下（h/H=0.2），分別分析晃蕩沖擊荷載的特征壓力值隨外激頻率的變化關系。圖5給出傳感器Sensor1在兩組實驗中晃蕩沖擊荷載的特征壓力值隨外激頻率的變化關系。特征壓力值分別是最大峰值壓力（Pmax）、所有壓力峰值的平均值為（Pmean）、壓力峰值按大小排序后的第1/10個特征壓力值（P1/10），壓力峰值按大小排序后的第1/3個特征壓力值（P1/3）。從圖5中可以看出，f/f1=1.0時，Pmean、P1/10和P1/3在六自由度平臺的實驗結果要略大于在單自由度平臺的實驗結果；當f/f1=1.1時，Pmax、Pmean、P1/10和P1/3在六自由度平臺的實驗結果要明顯大于在單自由度平臺的實驗結果。

圖6分別給出靜水面處監測傳感器Sensor2在兩組實驗中晃蕩沖擊荷載的特征值隨外激頻率的變化關系。從圖中可以看出，f/f1=0.9、1.0和1.1時，Pmax在兩次實驗的結果都存在較大差異，同時在f/f1=1.1時，Pmean、P1/10和P1/3六自由度平臺的實驗結果均要大于單自由度平臺的實驗結果，由其對應的壓力時程曲線圖4（b），可以看出，六自由度平臺實驗的每一次沖擊峰值都明顯大于單自由度平臺的實驗結果。究其主要原因，一是由于六自由度平臺實際運動位移幅值要大于單自由度平臺，而晃蕩沖擊荷載峰值對外激激勵幅值非常敏感；二是對于低載液率，晃蕩隨機性和非線性更加顯著，同時沖擊波也會在靜水面上下附近發生破碎，都導致了兩次實驗的對比結果在某些工況下的差異。

3.3 晃蕩沖擊荷載與外激幅值的關系

中載液工況下（h/H=0.6），分別討論晃蕩沖擊荷載的特征壓力值隨外激幅值的變化關系。如圖7 （a）、（b），分別給出，f/f1=1.0，A=30 mm工況下，監測傳感器Sensor5及Sensor6在兩組實驗中晃蕩沖擊荷載的特征值與外激幅值的關系。從圖中可以看出，Pmax、Pmean、P1/10和P1/3在六自由度平臺的實驗結果要大于在單自由度平臺的實驗結果，尤其對于靜水面處的傳感器Sensor6，其峰值最大值在兩次實驗中具有明顯差別。對于f/f1=1.0和A=40 mm工況，Sensor5及Sensor6的實驗結果則是具有相反的結論，如圖7（c）、（d）所示。

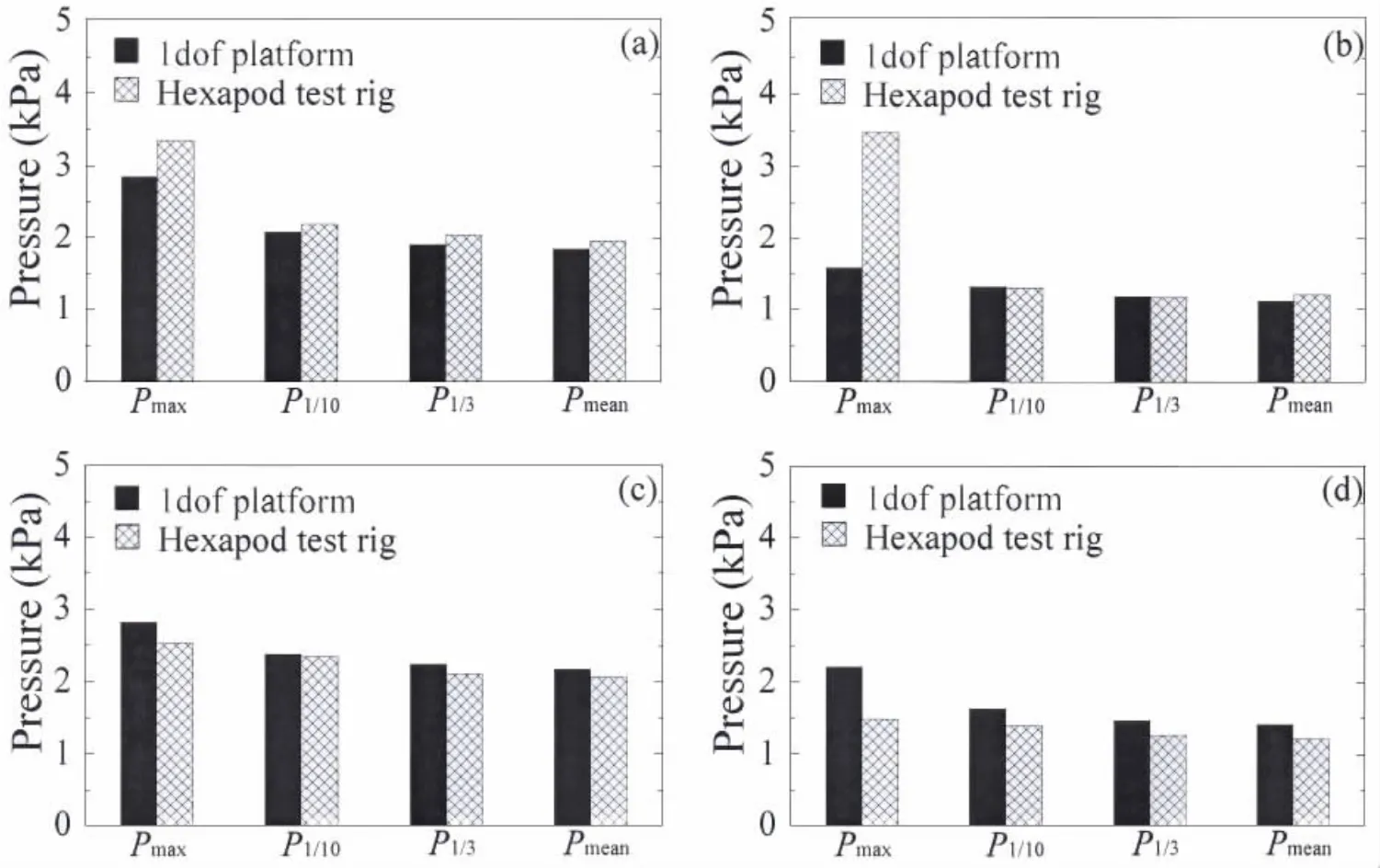
圖7 晃蕩沖擊荷載與外激幅值的關系：（a）工況C9 Sensor5；（b）工況C9 Sensor6；（c）工況C10 Sensor5；（d）工況C10 Sensor6Fig.7 The relationship between sloshing impact loads and oscillation amplitude:(a)C9 Sensor5;(b)C9 Sensor6; (c)C10 Sensor5;(d)C10 Sensor6

4 結 論

為了研究不同類型運動平臺的運動性能及其對儲液艙內液體晃蕩沖擊載荷的影響，本文以大比尺二維矩形艙為模型，分別在單自由度運動平臺和六自由度運動平臺開展了系統的液體晃蕩沖擊實驗，獲得結論如下：

（1）六自由度運動平臺在完成單個方向運動時會引起其他五個自由度的微小相對運動，導致其精度要略低于單自由度運動平臺。本文建議在晃蕩模型實驗外激激勵為單個自由度時，最好采用單自由度運動平臺，而在完成多自由度耦合實驗時可采用六自由度運動平臺。

（2）對比了兩次實驗的沖擊荷載時程曲線，荷載峰值一是不可能都完全同時發生，二是即使同時發生沖擊作用，其峰值也不能完全相同，但是就晃蕩沖擊壓力形式而言是可以保持一致的。

（3）即使在最簡單的規則橫蕩激勵下，沖擊壓力表現出了一定的隨機性。其中，晃蕩沖擊荷載的最大峰值Pmax在兩組實驗中不是十分吻合，且Pmean，P1/10和P1/3在兩次實驗的結果也存在差微。但由于晃蕩的隨機性，難以完全避免這些細微的差別。建議實驗開展前，對運動平臺進行系統誤差分析，以保證實驗結果的精確性。

[1]Floating Offshore Liquefied Gas Terminals[R].American Bureau of Shipping,2010.

[2]Kuo J F,Campbell R B,Ding Z,et al.LNG tank sloshing assessment methodology-the new generation[C]//Proceedings of the 19th International Conference on Offshore Mechanics and Arctic Engineering.Osaka,Japan:The International Society of Offshore and Polar Engineers,2009.

[3]岳寶增,祝樂梅,于 丹.儲液罐動力學與控制研究進展[J].力學進展,2011,41(1):79-92. Yue Baozeng,Zhu Lemei,Yu Dan.Recent advances in liquid-filled tank dynamics and control[J].Advances in Mechanics,2011,41(1):79-92.(in Chinese)

[4]王德禹.液化天然氣船液艙的晃蕩[J].計算機輔助工程,2010,19(3):1-4. Wang Deyu.Sloshing in LNG carriers tanks[J].Computer Aided Engineering,2010,19(3):1-4.(in Chinese)

[5]Faltinsen O M,Timokha A N.Sloshing[M].Cambridge:Cambridge University Press,2009:548-550.

[6]衛志軍,岳前進,阮詩倫等.矩形液艙晃蕩沖擊載荷的實驗機理研究[J].船舶力學,2012,16(8):885-892. Wei Zhijun,Yue Qianjin,Ruan Shilun,et al.An experimental investigation of liquid sloshing impact load on a rectangular tank[J].Journal of Ship Mechanics,2012,16(8):885-892.(in Chinese)

[7]Zhu R Q,Wu Y S,Incecik A.Numerical simulation of liquid sloshing-a review[J].Shipbuilding of China,2004,45(2): 14-27.

[8]Graczyk M,Moan T.A probabilistic assessment of design sloshing pressure time histories in LNG tanks[J].Ocean Engineering,2008,35:834-855.

[9]Pistani F,Thiagarajan K.Set-up of a sloshing laboratory at the University of Western Australia[C]//Proceedings of the 20th International Conference on Offshore Mechanics and Arctic Engineering.Beijing,China:The International Society International Society of Offshore and Polar Engineers,2010.

[10]Loysel T,Chollet S,Gervaise E,et al.Results of the first sloshing model test benchmark[C]//Proceedings of the 29th International Conference on Offshore Mechanics and Arctic Engineering.Rhodes,Greece:The International Society International Society of Offshore and Polar Engineers,2012.

[11]陳穗康,顧樹華,戴李民.矩形水艙流體晃蕩的水動力特性的試驗研究[J].中國造船,1984,(85):35-41. Chen Suikang,Gu Shuhua,Dai Limin.Experimental investigation on the hydrodynamic characteristics of liquid sloshing loads in rectangular tanks[J].Shipbuilding of China,1984,(85):35-41.(in Chinese)

[12]王德禹,李龍淵,施 其.三自由度晃蕩模擬裝置及其模態分析[J].海洋工程,2000,18(4):94-96. Wang Deyu,Li Longyuan,Shi Qi.3 Freedom sloshing simulator device and its modal analysis[J].Ocean Engineering, 2000,18(4):94-96.

[13]繆泉明,匡曉峰.702所海洋工程水動力模型試驗技術進展介紹[C].紀念顧懋祥院士海洋工程學術研討會論文集, 2011:9-23.

[14]衛志軍,岳前進,張文首等.大尺度儲艙內流體晃蕩砰擊壓力的測量方法研究[J].中國科學,2014.(已錄用). Wei Zhijun,Yue Qianjin,Zhang Wenshou,et,al.Experimental investigation of violent slamming pressure in large-scaled tank[J].SCIENTIA SINICA Phys,Mech&Astron,2014.(Accepted).

[15]Thiagarajan K P,Rakshit D,Repalle N.The air-water sloshing problem:Fundamental analysis and parametric studies on excitation and fill levels[J].Ocean Engineering,2011,38(2):498-508.

[16]Repalle N,Truong T,Thiagarajan K,et al.The effect of sampling rate on the statistics of impact pressure[C]//Proceedings of the 29th International Conference on Ocean,Offshore and Arctic Engineering.Shanghai,China:American Society of Mechanical Engineers,2010.

[17]Gavory T,De Seze P E.Sloshing in membrane LNG carriers and its consequences from a designer’s perspective[C]//Proceedings of the 19th International Conference on Offshore Mechanics and Arctic Engineering.Osaka,Japan:The International Society,2009.

An experimental study of slamming impact load on two platforms

WEI Zhi-jun,CHEN Xiao-dong,DONG Yu-shan,TANG Bin,YUE Qian-jin
(State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116023,China)

Impact loads caused by liquid sloshing are related to the filling level and excitation parameters (such as excitation amplitude and period)of the tank.The large-scale sloshing model experimental method is the most reliable approach to study impact loads,which can realize tank motion in the laboratory by the test rig.Hence,the performance and accuracy of the employed test platform is very important.In order to investigate the performance and the effect of single degree-of-freedom(1 dof)platform and hexapod test rig on slamming impact pressure,this paper focuses on a comparatively experimental study in a large-scaled two-dimensional rectangular tank.A series of sloshing tests was designed and conducted with the same regular sway excitation,measurement set-up and filling level.The results show that the 1dof platform has higher accuracy for lateral motion.Furthermore,there exist significant discrepancies on pressure time history and pressure characteristic values under some conditions.Even though,the general trend of impact pressure is the same.These experimental results can give an indicator for choosing test rig for large-scaled sloshing model experiments.

large-scaled model tests;performance of test rig;slamming impact load;comparative study

TV131.66

A

10.3969/j.issn.1007-7294.2015.07.010

1007-7294（2015）07-0841-09

2015-03-26

國家科技重大專項項目（2011ZX05026-006-06），創新研究群體基金資助（50921001）

衛志軍（1985-），女，博士研究生，E-mail：weizj@mail.dlut.edu.cn；

陳曉東（1987-），男，碩士生。