基于模糊PID控制算法的導盲機器人研究

張志美, 程立英, 趙以恒, 吳海元

(沈陽師范大學 物理科學與技術學院, 沈陽 110034)

?

基于模糊PID控制算法的導盲機器人研究

張志美, 程立英, 趙以恒, 吳海元

(沈陽師范大學 物理科學與技術學院, 沈陽 110034)

結合PID控制對線性定常系統控制的優越性和模糊控制器對復雜非線性系統的有效控制,設計了一種基于模糊PID控制算法實現導盲機器人的避障循跡控制。導盲機器人采用樂高套件搭建而成,避障環節設計采用超聲波傳感器檢測障礙物信息,控制器采集障礙物信息及機器人行駛速度信息,利用模糊PID算法實現避障;循跡環節為克服遇機器人轉彎或高速行進時一般PID控制算法穩定性差的不足,采用實時跟蹤偏差和偏差變化率來修正PID控制的各個參數,實現對機器人的導航控制,其中機構采用紅外傳感器進行識別檢測。實驗結果表明,利用改進算法進行導盲機器人的避障循跡控制,能夠極大的提高避障的準確率,精準的循跡。

模糊PID算法; 導盲機器人; 循跡避障

0 引 言

隨著社會生產技術的不斷發展,機器人的應用領域也在不斷擴展。機器人正跳脫以往在生產中負責生產、制造、搬運等任務的范疇,從傳統的工業型走向服務型。導盲機器人[1]是服務型機器人,專為盲人設計,主要功能實現循跡、避障與交通路口的紅綠燈辨別。機器人避障問題是當今機器人研究領域的一個焦點問題,在避開障礙物的過程中,機器人經常面臨無法預測環境變化的問題,這是由于機器人從傳感器[2]所得到的信號是不連續的、不安全的、不可靠的,所以這就造成了機器人避障成為當今機器人研究領域的焦點[3]。國內在研究機器人的避障及路徑規劃方面起步較晚,現階段的大多數研究也都處于單項研究階段。目前常用的控制算法是將遺傳算法、模糊控制以及神經網絡等人工智能方法等應用到PID控制算法中[4-6],以提高避障精度、加快規劃速度從而滿足實際應用需求。

由于本設計是基于導盲機器人的避障循跡控制研究,系統要求所設計的控制算法具有實時性好、處理速度快、辨識精度高。由于智能算法如BP神經網絡、遺傳算法的實時性差,本設計采用模糊控制算法與PID算法的結合,即模糊PID算法[7-8],并改進模糊控制參數,使得系統具有良好的實時性,且處理速度快,由于其處理的高效性提高了系統對避障參數的處理和分析能力,進一步提升了系統避障的能力。

1 改進的模糊PID算法

模糊控制是智能控制的一種典型的重要分支,它不依賴于被控對象的數學模型,主要依靠現場操作人員或相關專家的判斷、經驗或歷史數據等先驗知識,實現對系統的實時控制。

基本PID算法因其依賴被控對象精確的數學模型,對非線性、時變的復雜控制系統及控制環境復雜的系統難以獲得滿意的效果。模糊PID算法是結合模糊控制與PID算法,通過建立相應的模糊控制表,根據系統偏差、偏差變化率查表得到比例、積分和微分的系數3個參數的整定值,實現PID運算。控制的關鍵是根據實時環境、專家經驗等因素建立模糊控制表。圖1所示模糊PID控制系統框圖。

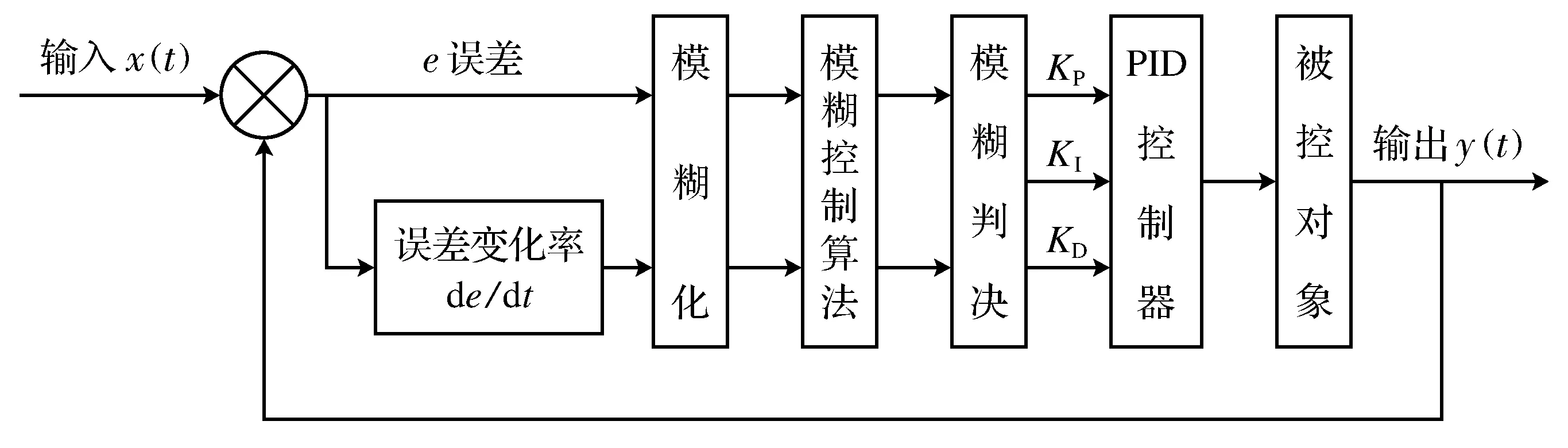
圖1 模糊PID控制系統框圖

模糊PID控制系統[8-11]以被控對象的反饋值與目標值的誤差e(t)和誤差變化率de(t)/dt作為系統輸入,采用模糊算法對PID參數進行實時調整,以滿足實際控制環境對被控對象的要求,具有良好的適應能力。

2 導盲機器人循跡算法設計

導盲機器人循跡過程中在轉彎或高速運動的情況下,常規PID算法的穩定性差[12-14]。本設計采用實時跟蹤偏差和偏差變化率來修正PID控制的各個參數,即模糊PID控制算法實現對機器人的控制。

PID算法表示如下:

其中:KP為比例系數;KI為積分系數;KD為微分系數。模糊自整定PID參數的目的是使參數KP、KI、KD隨著誤差e(t)和誤差變化率de(t)/dt的變化而自行調整。

根據導盲機器人的控制要求,將系統誤差e(t)和誤差變化率de(t)/dt作為模糊控制的輸入語言變量,KP、KI、KD作為輸出語言變量。為提高控制器主動適應系統或環境的能力,控制器參數KP、KI、KD的初值由用戶根據環境因素及經驗輸入,提高用戶對控制參數的宏調節能力,彌補模糊推理中對變量進行模糊化所造成的誤差。其中5個語言變量的量化等級定為7級,即e(t)、de(t)/dt、KP、KI、KD={-3,-2,-1,0,1,2,3},模糊子集為{NB,NM,NS,O,PS,PM,PB},對應值代表負大,負中,負小,零,正小,正中,正大。模糊集上的基本論域變化范圍為{-3,3},將基本論域范圍連續變化的量分級離散化,量化方式采用非線性量化,然后進行模糊處理。本系統采用三角形隸屬度函數,以簡化模糊推理的計算過程。表1所示輸入輸出變量的隸屬度函數表。

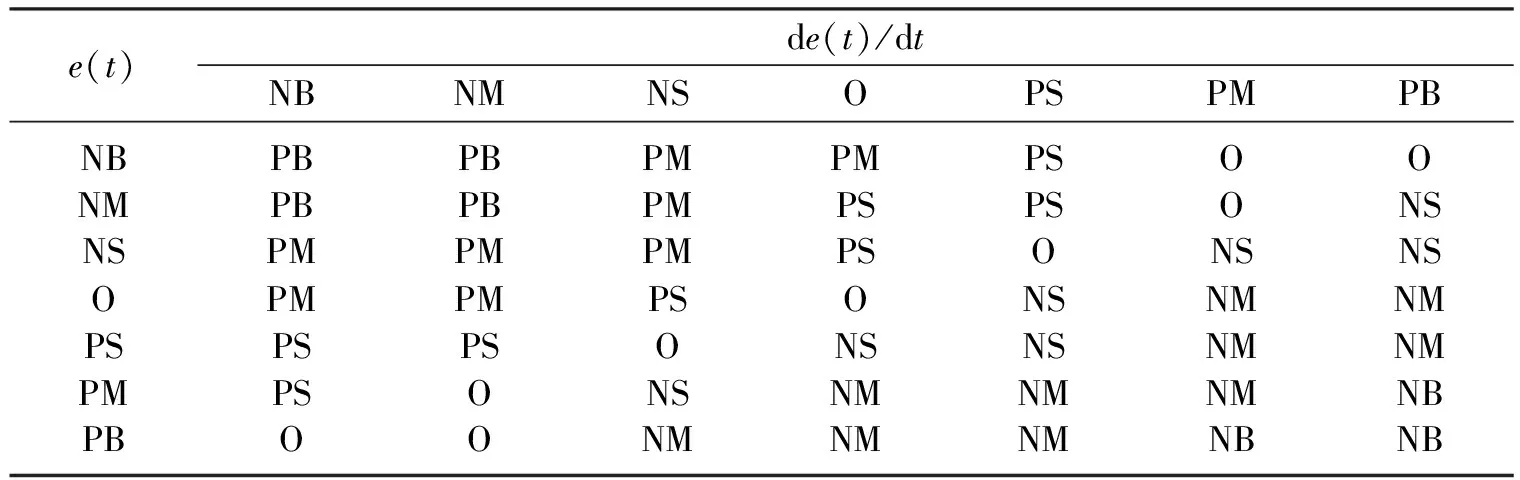
表1 誤差e(t),誤差變化率de(t)/dt,KP,KD,KI隸屬度表

根據導盲機器人控制經驗采用如下規則:

1) 當軌跡誤差e(t)較大時,為了加快循跡的響應速度,取較大的KP;同時為了避免由于運行中對于直角轉彎區誤差e(t)瞬時變大可能出現的微分飽和而使控制作用超出許可的范圍,導致超調的發生,應取較小的KP;若系統響應出現較大的超調,產生積分飽和,此時令KP=0去掉積分作用。

2) 當誤差|e(t)|和誤差變化率|de(t)/dt|大小適中時,KP應取得小些,確保系統響應具有較小的超調。KD和KI應取值適合,此時KD對系統響應的影響較大。

3) 當誤差|e(t)|較小時,為提高系統的穩態性能,KP和KI均取大些。考慮到系統的抗干擾性能,避免系統在設定值附近出現振蕩,當|de(t)/dt|較小時,KD取大些,|de(t)/dt|較大時,KD取小些。

4) 誤差變化率|de(t)/dt|表明導盲機器人循跡誤差變化的快慢速度,|de(t)/dt|越大,KP取值越小,KI取值越大。

系統建立ΔKP,ΔKI,ΔKD的控制規則表如表2所示。

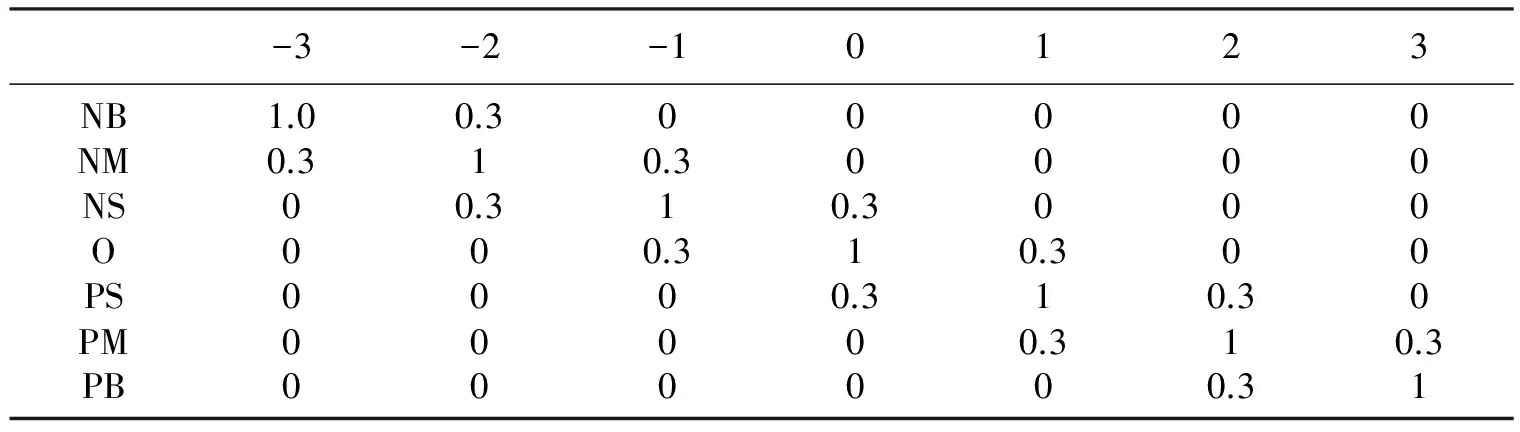
表2 模糊變量ΔKP的模糊規則表

表3 模糊變量ΔKI的模糊規則表

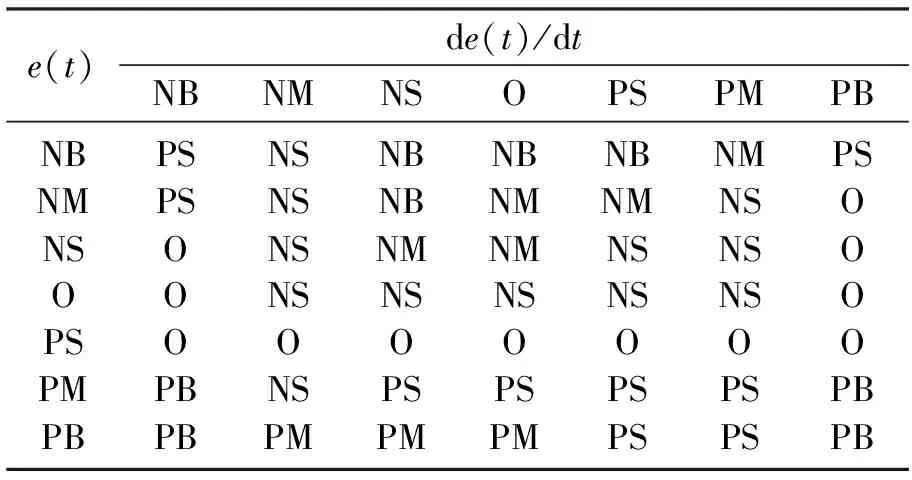
表4 模糊變量ΔKD的模糊規則表

通過查詢模糊控制表得到PID參數的修正量ΔKP,ΔKI和ΔKD,其相應的參數計算如下:

KP=KP0+ΔKP

KI=KI0+ΔKI

KD=KD0+ΔKD

式中:KP0,KI0,KD0是PID控制器的初值,一般根據現場調試經驗設定。

3 仿真實驗與硬件實現

3.1 基于模糊PID控制算法的仿真實現導盲機器人的避障循跡控制

系統采用傳統的PID控制,仿真結構圖如圖2所示。

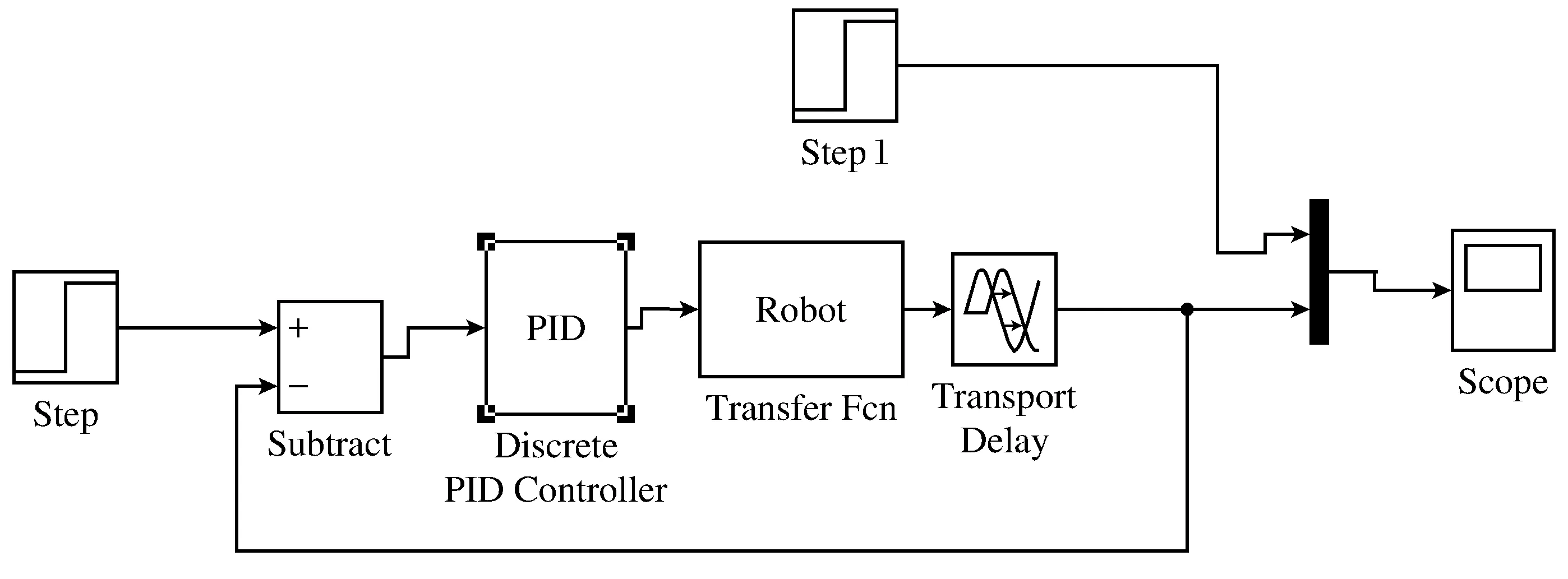
圖2 PID控制系統仿真結構圖

圖3 PID控制響應曲線

在圖中的PID模塊中對3個參數進行設定,通過不斷調整PID三參數,得到最佳仿真曲線,其中,KP=2,KI=0.018,KD=0.01,仿真結果如圖3所示。

圖3反映導盲機器人循跡的響應曲線,橫軸為響應時間t,單位為ms,縱軸為階躍響應h(t)。由圖可知調節時間為0.4 ms,超調量約20%左右,穩態誤差為0。

采用模糊PID控制,系統仿真結構如圖4所示。

圖4 模糊PID控制系統仿真結構

仿真結果如圖5所示,調節時間為0.18 ms,超調量為0,穩態誤差為0。

3.2 導盲機器人硬件系統調試

系統采用樂高機器人套件[15-16]組合,硬件結構如圖6所示。

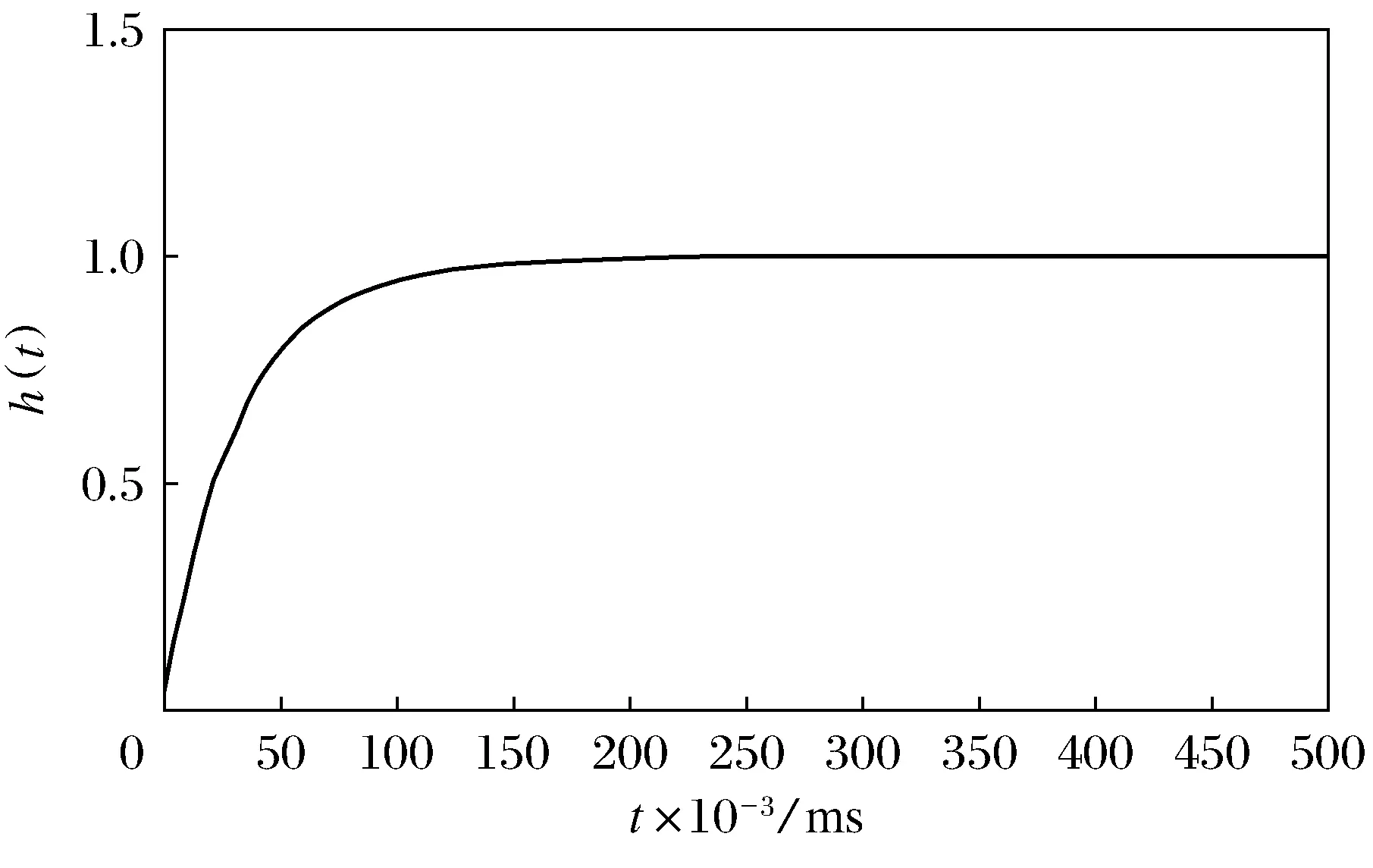
圖5 模糊PID控制響應曲線

圖6 導盲機器人硬件結構圖

系統在樂高NXT軟件環境下編程控制,控制結構如圖7所示。

圖7 導盲機器人循跡避障結構圖

圖8 循跡現場測試圖

實驗采用上述模糊PID調節控制機器人的循跡,循跡如圖8所示。根據現場測試機器人在轉彎和急速運行中的穩定性好,較好地實現精確循跡,快速反應,繞過障礙物后能快速回到循跡路線上。

通過對導盲機器人的調試,測試軌跡在黑色硬紙條的軌道上進行的,用紙箱作為障礙物,循跡避障測試5次,軌道長度約2 m,結果如表5所示。

表5 測試結果

4 結 語

從測試結果可以看出,采用模糊PID控制算法,小車的循跡與避障速度大大提高。小車能很好的完成循跡功能,對于s道和直角道,軌跡小車能良好地完成循跡功能。由于算法不具備自學習的能力,對于隨機障礙物的避障能力還有待提高。今后將進一步改進系統結構與算法的自學習能力,提高導盲機器人的循跡避障能力,為盲人提供切實有效的幫助。

[1]黃大志,申屠留芳,郭燕.導盲機器人中超聲波測距系統的研究[J].淮海工學院學報:自然科學版, 2009,18(1):19-22.

[2]王俊峰,孟令啟.超聲波傳感器應用技術[M].北京:機械工業出版社, 2006.

[3]常健,吳成東,李斌.移動機器人避障方法綜述[J].儀器儀表學報, 2010,31(8):439-442.

[4]徐兆棣,李曉毅.線性時滯系統時滯相關穩定性分析研究進展[J].沈陽師范大學學報:自然科學版, 2013,31(2):162-168.

[5]王達開.基于backstepping的自適應模糊控制及應用[J].沈陽師范大學學報:自然科學版, 2013,31(2):192-195.

[6]田琦,李琪,姚鵬,等.基于模糊PID的全方位移動機器人運動控制[J].電子科技, 2011,24(9):131-133,139.

[7]王述彥,師宇,馮忠緒.基于模糊PID控制器的控制方法研究[J].機械科學與技術, 2011,30(1):166-172.

[8]張涇周,楊偉靜,張安祥.模糊自適應PID控制的研究及應用仿真[J].計算機仿真, 2009,26(9):132-135.

[9]陸華才,徐月同,劉鵬鵬,等.永磁直線同步電機進給系統模糊PID控制[J].電工技術學報, 2007,22(4):59-63.

[10]樊開陽,林小蘭.基于Matlab GUI的直流電機PID調速系統的設計[J].微型機與應用, 2013,32(22):62-65.

[11]王葳,張永科,劉鵬鵬,等.無刷直流電機模糊PID控制系統研究與仿真[J].計算機仿真, 2012,29(4):196-199.

[12]田淑杭,姜麗娟.一種參數自整定模糊PID控制器的研究[J].電氣傳動自動化, 2003,25(6):28-30.

[13]駱德淵,劉榮,李紀文.采用模糊邏輯的移動機器人軌跡跟蹤[J].電子科技大學學報, 2008,37(6):943-946.

[14]高健,黃心漢,彭剛,等.移動機器人PID運動控制器參數的模糊自整定[J].華中科技大學學報:自然科學版, 2004,32(增刊):48-51.

[15]趙子愷.LEGO機器人的編程控制[J].中國計量學院學報, 2004,15(1):44-48.

[16]宮廣驊.玩轉樂高機器人[M].北京:人民郵電出版社, 2014.

Fuzzy-PID arithmetic for blind guiding robots

ZHANGZhimei,CHENGLiying,ZHAOYiheng,WUHaiyuan

(College of Physics Science and Technology, Shenyang Normal University, Shenyang 110034, China)

Combining the PID superiority for constant linear systems and effective control of fuzzy controller for complex nonlinear systems, A fuzzy-PID arithmetic was applied in blind guiding robots to realize intelligent tracking and obstacle-avoiding.The blind guiding robot used LEGO robot kit, obstacle-avoid link used ultrasonic sensors to detect obstacles information, the controller collected obstacle information and robot speed information to realize obstacle-avoid by using fuzzy-PID arithmetic.Intelligent tracking used real-time tracking deviation and rate of deviation to modify the PID parameters.The recognition detection used infrared sensors.Final examples show that improved fuzzy PID control arithmetic can greatly increase the accuracy of obstacle avoidance and track accurately.

Fuzzy-PID arithmetic; blind guiding robots; track

2014-09-20。

遼寧省教育廳科學技術研究項目(L2012391)。

張志美(1982-),女,河北尚義人,沈陽師范大學講師,東北大學博士研究生。

1673-5862(2015)01-0081-05

TP273.4

A

10.3969/ j.issn.1673-5862.2015.01.018