水準測量中海潮負荷改正的計算

徐新強，趙德軍

測繪信息技術總站，陜西 西安，710054

?

水準測量中海潮負荷改正的計算

徐新強，趙德軍

測繪信息技術總站，陜西 西安，710054

本文詳細推導了由海潮模型和格林函數卷積積分計算傾斜負荷效應的公式，給出了切實可行的計算方法；同時，利用NAO99b全球海潮模型，采用Farrell積分格林函數法，計算了部分地區傾斜負荷潮及部分沿海水準的海潮負荷改正值。本文給出的計算方法適合于高等級水準計算。

水準；海潮負荷(OTL)；傾斜負荷；海潮模型；格林函數

1 引 言

固體地球除受引潮力的直接作用而發生垂直和水平位移外，還受海洋潮汐產生的周期性負荷的作用而發生垂直和水平位移。研究表明，海潮負荷效應(Ocean Tidal Loading，OTL)包括[1]：(1)海水的直接引力；(2)在海水引力和壓力的作用下產生的地殼變形；(3)上述變形使得質量重新分布而產生的附加位。

文獻[2,3]用CSR系列海潮模型計算了高等級水準路線上的海潮負荷改正，并得出在我國近海地區，水準環閉合差能夠得到改善的結論。2006年發布的國標中明確要求一、二等水準測量數據處理時要進行OTL改正，并建議使用CSR4.0+CS(China Sea)或精度更高的海潮模型[4]，但對南北、東西傾斜分量的計算僅給出2個基本計算公式，對其中涉及到的大量參數的計算沒有描述，缺乏可操作性。鑒于此，本文給出了實用、切實可行的計算方法。

2 傾斜負荷潮計算方法

高精度水準計算中，海潮改正公式為[4]：

L=(ξcosA+ηsinA)S

(1)

式中，ξ、η分別為海潮負荷引起的計算點的南北、東西傾斜分量；A為水準路線方向的方位角；S為測段長度。對于水準路線來說，A，S是已知的，關鍵是如何求傾斜分量ξ和η。

傾斜負荷潮嚴格計算式如下[1,5,6,7]：

(2)

其中：

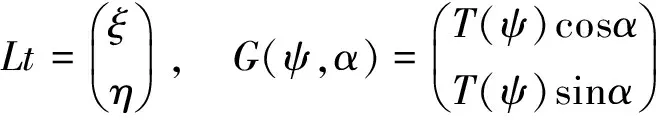
式中，θ、λ分別是負荷點的余緯和經度；t是世界時；R是地球平均半徑；ρ是平均海水密度；α是計算點到負荷點(θ，λ)的方位角；ψ是計算點到負荷點的球面角距。G(ψ,α)是質量負荷格林函數，T(ψ)是傾斜負荷格林函數。瞬時海潮高H(θ,λ,t)可以分解成調和分潮之和[1]：

(3)

其中：

Hcp(θ,λ)=ζp(θ,λ)cosδp

Hsp(θ,λ)=ζp(θ,λ)sinδp

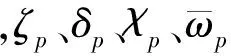
(4)

式(4)即文獻[4]中的(D.22)式，其中：

(5)

而：

tanβp=LSp/LCp

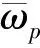
表1 主要調和分潮的角速度，單位：°/h

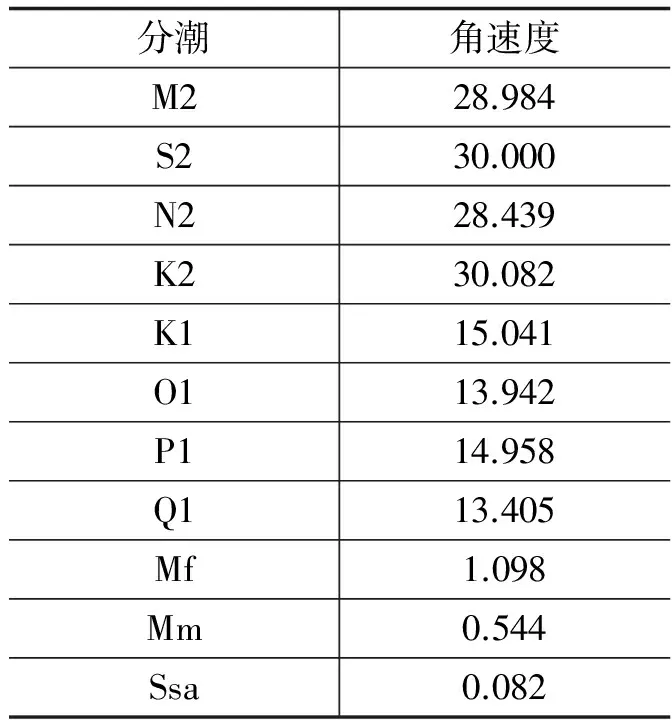
分潮角速度M228．984S230．000N228．439K230．082K115．041O113．942P114．958Q113．405Mf1．098Mm0．544Ssa0．082

天文輻角χp是天文引數的線性組合，通過下式來計算[1]：

χM2=2h-2s

χS2=0

χN2=2h-3s+q

χK2=2h

χK1=h+90°

χO1=h-3s+q-90°

χMf=2s

χMm=s-q

χSsa=2h

式中，天文引數s、h、q分別表示月亮的平黃經、太陽的平黃經和月亮升交點經度[1]：

h=279.69668°+36000.76892°T-0.00030°T2

s=270.43659°+481267.89057°T+0.00113°T2

q=334.32956°+4046.03403°T-0.01032°T2式中，T為儒略世紀數，從1973年起算。

3 數值計算

3.1 海潮模型的選擇

海潮負荷引起的傾斜精度主要取決于海潮模型、格林函數以及數值積分方法[8,9]。NLOADF提供了多種地球模型的格林函數，并且采用完全高斯數值積分的方法計算式(5)，因此，傾斜負荷的精度取決于海潮模型的精度和分辨率[9]。隨著衛星測高技術的發展，先后出現了CRS3.0、CRS4.0、AG95、GOT、NAO、FES2004、TPXO7等多種海潮模型。文獻[11]利用304個全球驗潮站、137個中國東海驗潮站和63個南海驗潮站多年的觀測資料，分析對比了幾種目前具有代表性的海潮模型，認為NAO99b在中國海域精度最高。文獻[12]用GPS觀測資料分析對比了多種海潮模型，認為NAO99b 在我國黃海、東海、南海和印尼海域具有較高精度。NAO99b是日本國家天文臺基于二維非線性淺水方程，采用Blending方法同化日本韓國沿岸驗潮站和5年T/P沿軌海面高數據建立的全球以及日本周邊局部海潮模型[11]。

3.2 傾斜負荷潮計算

表2 M2分潮東西向傾斜分量，單位：振幅 nrad，相位°

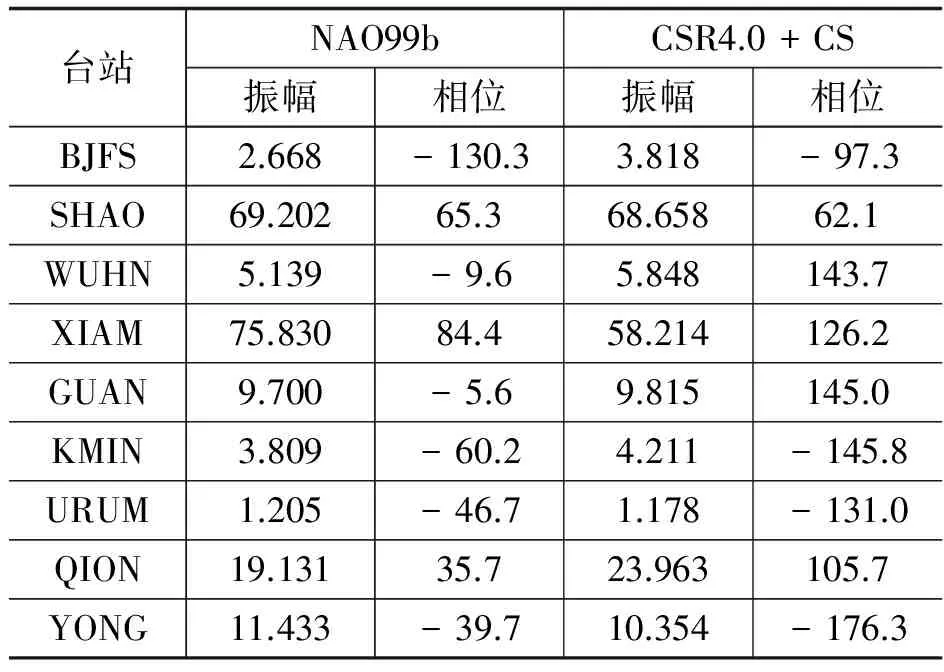
臺站NAO99bCSR4．0+CS振幅相位振幅相位BJFS2．668-130．33．818-97．3SHAO69．20265．368．65862．1WUHN5．139-9．65．848143．7XIAM75．83084．458．214126．2GUAN9．700-5．69．815145．0KMIN3．809-60．24．211-145．8URUM1．205-46．71．178-131．0QION19．13135．723．963105．7YONG11．433-39．710．354-176．3

為了與文獻[6]做對比分析，采用標準的GBA平均地球模型計算部分地殼運動觀測網絡臺站，M2分潮東西方向傾斜負荷效應的影響(即η)，采用NAO99b模型計算，其中CSR4.0+CS模型計算結果來自文獻[6]。注意：按式(2)計算的傾斜負荷效應(ξ，η)的振幅分別以南、西方向為正，振幅的單位是nrad(即10-9弧度)，相位的單位是度。由表2可知OTL對沿海地區傾斜潮的影響特別顯著，可達數十nrad；對內陸的影響在幾nrad量級，如SHAO的振幅達到69.202nrad，而URUM則只有1.205nrad。不同海潮模型的計算結果有一定的差異，這是由于復雜的近海海岸形狀、海底地形和特殊的海灣條件導致海潮模型有一定差異[1]。

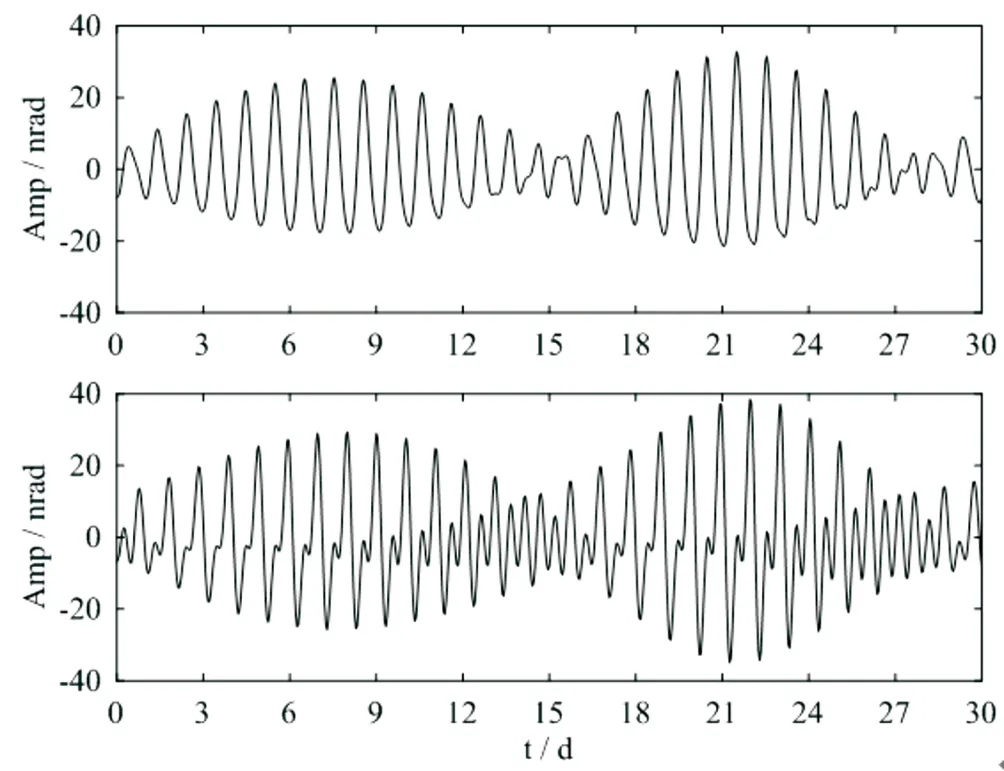
圖1 永興島傾斜分量隨時間變化圖

由式(4)可知，已知測站的位置和觀測時間，將各個分波的傾斜負荷疊加就能算出海潮對測站的傾斜分量。圖1給出了永興島的傾斜分量時間序列圖，時間從2013年7月1日至7月30日共720小時。上圖為東西傾斜分量，下圖為南北分量。

3.3 水準測量中的海潮負荷改正

本文收集了國家海島礁一期測繪工程沿海200多條二等水準測段數據，海潮模型采用NAO99b。海潮負荷改正與水準路線位置和觀測時間有關，因此給出了水準測段往返測的OTL改正值(表3)。從中可以看出往測92.5%、返測93.7%的測段改正值小于0.05mm。往返測平均改正值的絕對值分別為0.019mm和0.023mm，由于此值已比其它系統誤差改正值大(如視準軸誤差、地球曲率改正)，因此必須進行OTL改正。但是，OTL對水準路線改正值不太明顯，因為水準測量中OTL改正一般只占到固體潮改正的10%[1]。

表3 水準測段往返測OTL改正值

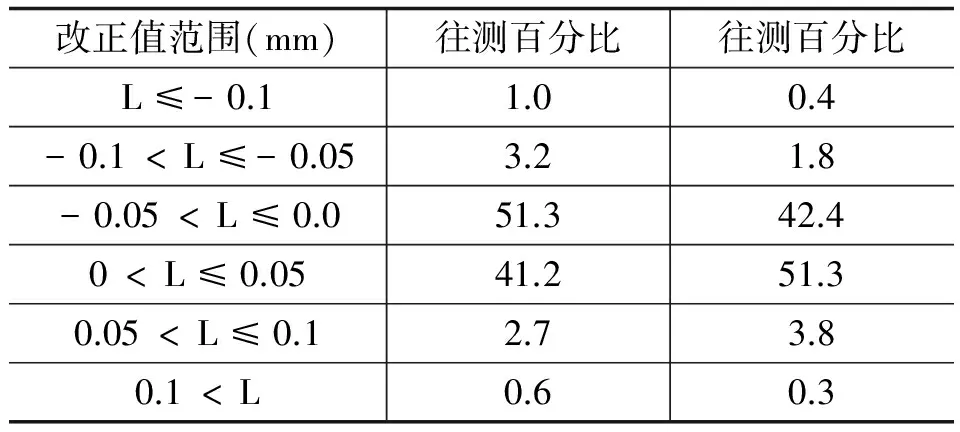
改正值范圍(mm)往測百分比往測百分比L≤-0．11．00．4-0．1

由式(1)知，改正值除了與ξ和η有關外，還與水準路線的方位角、測段長度和觀測時間有關，因此，同一地區的測段及其改正值也有一定的差異。由于缺乏高等級的水準數據，本文沒有計算海潮改正對水準環閉合差的影響，文獻[3]認為海潮負荷改正對水準環閉合差的影響不大，一般在5mm以內。

4 結 論

通過理論分析和數值計算得出以下結論：

(1)OTL對傾斜影響的振幅可達到幾nrad，沿海地區可達10nrad或更多，并且隨測區離海洋的距離增加而減少，靠海洋越近則影響越大。同一地區的測段及其改正值也有一定的差異，這是因為改正值還與水準測段的方位角以及觀測時間有關。

(2)不同海潮模型計算的傾斜影響間存在一定的差異，這與近海海岸線形狀、海底地形和特殊的海灣條件等因素有關。有條件的情況下，盡量使用驗潮站實測的海潮資料修正全球模型，或用實測數據評估全球海潮模型。

(3)雖然OTL改正值很小，但部分測段的改正值大于其它系統誤差改正值，因此，高精度水準計算時必須加入OTL改正。

[1]中國科學院測量與地球物理研究所．固體潮論文集[M]．北京：測繪出版社，1988．

[2]董鴻聞，陳士銀，許大欣等．高精度水準測量的海潮負荷改正[J]．測繪通報，2000，7(3)：14-16．

[3]王文利，董鴻聞．用CSR4.0+CS模型計算海潮負荷改正[J]．大地測量與地球動力學，2003，23(4)：70-74．

[4]GB/T 12897-2006．國家一、二等水準測量規范[S]．北京：中國標準出版社，2006．

[5]周江存，許厚澤，孫和平．中國臺灣地區海洋負荷潮汐對重力、位移、傾斜和應變固體潮觀測的影響[J]．大地測量與地球動力學，2002，22(1)：81-86．

[6]孫和平，周江存，許厚澤．中國地殼運動觀測網絡基準站傾斜固體潮觀測中的海潮負荷信號改正問題[J]．地球物理學進展，2001，16(3)：21-39．

[7]周江存，孫和平．高精度GPS觀測中的負荷效應[J]．地球科學進展，2007，22(10)：1036-1040．

[8]Bos M S，Baker T F．An estimate of the errors in gravity ocean tide loading computations [J]．Journal of Geodesy，2005,79：50-63．

[9]Agnew D C．NLOADF: a program for computing ocean-tide loading. J Geophys Res, 1997, 102(B3)：5109-5110．

[10]暴景陽，許軍．中國沿岸驗潮站潮汐調和常數的精度評估[J]．海洋測繪，2013，33(1)：1-4．

[11]李大煒，李建成，金濤勇．利用驗潮站資料評估全球海潮模型的精度[J]．大地測量與地球動力學，2012，32(4)：106-110．

[12]趙紅，張勤，黃觀文．基于不同海潮模型研究海潮負荷對GPS精密定位的影響[J]．大地測量與地球動力學，2012，32(5)：108-112．

Calculation of Ocean Tidal Loading Correction in Leveling

Xu Xinqiang，Zhao Dejun

Technical Division of Surveying and Mapping, Xi’an 710054, China

This paper deduces the tilt loading effects formulae in detail based on the convolution integration approach of ocean tidal model and Green's function, and it presents the practical computing algorithms. Besides, the tilt loading in some area are calculated using the integral method of Farrell's Green's function, which adopts global tidal model NAO99b, and the ocean tidal loading correction in part of coastal areas are calculated. The computing algorithms presented in this paper are suitable for high accuracy leveling data.

leveling; ocean tidal loading (OTL); tilt loading; ocean tidal model; Green’s function

2015-01-16。

國家863計劃資助項目(2013AA122501)。

徐新強(1968—)，男，高級工程師，主要從事大地測量數據處理及地球重力場的研究。

P312.4

A