受迫振動的阻尼特性研究

杜全忠， 王 鵬， 王旭明， 姚 明

(1.寧夏大學 物理電氣信息學院，寧夏 銀川 750021；2.北方民族大學 基礎教育學院，寧夏 銀川 750021)

?

受迫振動的阻尼特性研究

杜全忠1， 王 鵬2， 王旭明1， 姚 明1

(1.寧夏大學 物理電氣信息學院，寧夏 銀川 750021；2.北方民族大學 基礎教育學院，寧夏 銀川 750021)

為有效詮釋不同阻尼條件下的受迫振動現象，采用波爾共振實驗儀開展了在不同阻尼，擺輪在彈性力矩、電磁阻尼力矩和強迫驅動力矩作用下，受迫振動的動力學實驗，并利用頻閃法測定動態的物理量——相位差。結果表明：不同阻尼條件下，幅頻特性具有選頻特性，驅動力矩角頻率與系統的固有角頻率相同時，振幅達到極大值，出現共振現象；共振振幅與阻尼系數呈負指數函數關系；物體振動位移變化與驅動力矩變化非同相位，共振時相位差900°。

阻尼特性； 受迫振動； 幅頻特性； 相頻特性

0 引 言

振動是物質運動的一種形式，物體在周期性外力持續作用下發生的振動稱為受迫振動，而該周期性外力也稱驅動力。對于一定的振動系統，如果驅動力是按簡諧振動的規律變化，且當振動系統達到穩定狀態時的受迫振動則變為簡諧振動。此時，其振動的周期即是驅動力的周期，振動的振幅保持恒定，且振幅的大小與驅動力的角頻率、振動系統的固有角頻率以及阻尼系數有關[1-2]。當驅動力的角頻率與系統的固有角頻率相同時，便產生共振現象，其振幅值達到最大[3]。受迫振動及其共振現象的情況在機械制造、建筑工程以及微觀科學研究等領域中隨處可見，如何利用其振動特性(既有破壞性，也有實用價值)解決工程中的問題，引起了工程技術人員的極大關注[4-6]。在實際系統中，諸多現象表現的是在不同阻尼條件下系統受迫振動的特性，所以研究阻尼系數對系統振動規律的影響就顯得尤為重要[7-11]。本文以擺輪的受迫振動實驗為例，探討不同阻尼系數對系統受迫振動規律的影響。

1 動力學理論及其方程

實驗研究對象為擺輪在彈性力作用下的自由擺，研究在電磁阻尼力矩作用下做受迫振動的特性。實驗過程中，當擺輪受到周期驅動力矩M=M0cosωt的作用。其中：M0是驅動力矩的振幅；ω是驅動力矩的角頻率。

考慮在電磁阻尼加空氣阻尼媒質中運動時的運動方程為

(1)

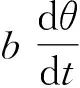
將方程(1)變為

(2)

對方程(2)求解可得：

(3)

θ=θ1e-βtcos(ωft+α)+

(4)

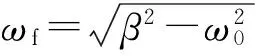
式(4)表明：擺輪的運動實質上是阻尼振動與簡諧振動兩個運動的合成。式(4)等式右邊的第一項表示阻尼振動，其隨時間的演化會逐漸消失；第二項表示簡諧振動。從能量角度看，驅動力矩不斷對擺輪做功，向振動體傳送能量，使之達到一個穩定的振動狀態。

擺輪振動的振幅為

(5)

擺輪的振幅與驅動力矩間的相位差為

(6)

可以看出，振動的振幅與相位差φ取決于β,ω,ω0和m，與振動的初始狀態無關。

由

(7)

從上述理論分析可以看出，阻尼系數β越小，系統的共振角頻率越接近于系統的固有角頻率，振幅θr也越大。

2 實驗方法與測量結果

2.1 實驗儀器

2.1.1 儀器

本實驗選用BG-2非智能型波耳共振儀[12](同濟大學物理實驗中心監制)，由實驗觀察受迫振動現象，定量測量與分析受迫振動的幅頻特性和相頻特性。該測試儀器由機械振動儀和電器控制箱兩部分組成，通過雙光電門測量周期和振幅，頻閃法測量相位差等。

2.1.2 測試關鍵性問題

實驗中應注意波耳共振儀的阻尼電流旋鈕旋向實驗時所需檔位等操作問題，此旋鈕某一檔位一旦選定后，在后期實驗過程中不能隨意改變該檔位或切斷整機電源，否則，由于電磁鐵剩磁現象將引起阻尼系數值的變化。只有在某一阻尼系數條件下的所有實驗數據(包括阻尼系數值和幅頻特性及相頻特性的測定)測試完畢后，需要改變阻尼系數值時方可改變該旋鈕檔位，這點對于實驗成敗至關重要[13-14]。

2.2 阻尼振動的觀測(測定β)

2.2.1 實驗測試

通過選擇阻尼電流旋鈕1～5各檔位，分別觀察在具體阻尼條件下振動系統振動的振幅衰減過程，同時通過電器控制箱測量系統的測量，記錄擺輪作具體阻尼振動時的振幅值θ1,θ2,…，θn和10個周期內的振動時間10T值。

2.2.2 實驗數據及數據處理結果

各阻尼電流檔位條件下測量數據記錄及數據處理結果見表1。其中，阻尼振動時振幅衰減按指數規律變化：θ=θ0e-βt。根據，

求出β值(見表1)，式中n為阻尼振動的周期次數，即θn為第n次振動時的振幅；T為阻尼振動測得10個周期時間的平均值。

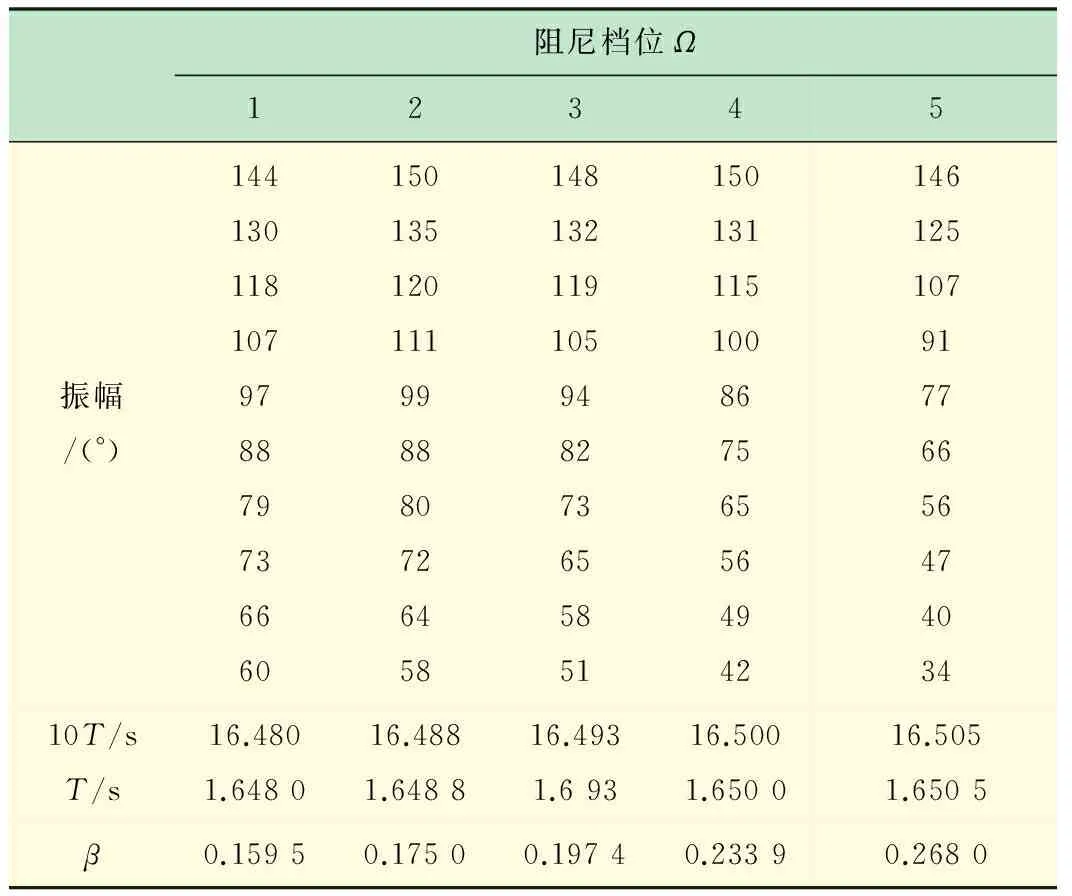
表1 阻尼振動的觀察及其阻尼系數測量數據

2.3 受迫振動幅頻特性與相頻特性的測定

2.3.1 實驗測試

(1)保持阻尼電流旋鈕檔位在原位置，打開電機。

(2)觀察受迫振動是否達到穩定狀態(周期檔位置于1，此時顯示數據為當前狀態，觀察擺輪周期與電機周期是否基本一致，且振幅值穩定)。

(3)利用頻閃法測定受迫振動振幅與驅動力矩間的相位差φ(測試前，將擺輪長凹槽和指針均調至光電門中央位置，否則會造成相位差的不穩定)。

(4)測量擺輪的周期和振幅(周期檔位置于10，測量打開，電器控制箱測量系統自動測量并顯示10T后的時間和振幅測量值)。

(5)精調驅動力周期旋鈕檔位，即改變電機轉速或周期，從而改變系統的振動狀態。

2.3.2 實驗關鍵性問題

(1)測量的相位差范圍一般在30°～150°，即調節驅動力周期旋鈕約在4～7。

(2)驅動力周期旋鈕始終朝一個方向緩慢并有序逐個調節。

(3)在共振點(相位差約在90°)附近，調節更應緩慢，數據測量更加密集且多為宜。

2.3.3 實驗數據及數據處理結果

測量數據及數據處理結果見表2(鑒于數據信息量大，在此只列出阻尼電流旋鈕檔位“1”條件下的測試數據，其他阻尼檔位條件下的數據略)。由測量數據可得幅頻特性[15-16]關系曲線和相頻特性[17]關系曲線，分別如圖1、2所示。

由圖1可以看到，在不同的阻尼作用下，振動系統的振幅都隨著ω/ω0的不同而變化：當兩者相差較大時，振幅較小；兩者相近時，振幅隨之增大，且ω/ω0=1時，振幅達到極大值，即驅動力矩的角頻率與系統的固有角頻率相同時發生共振。

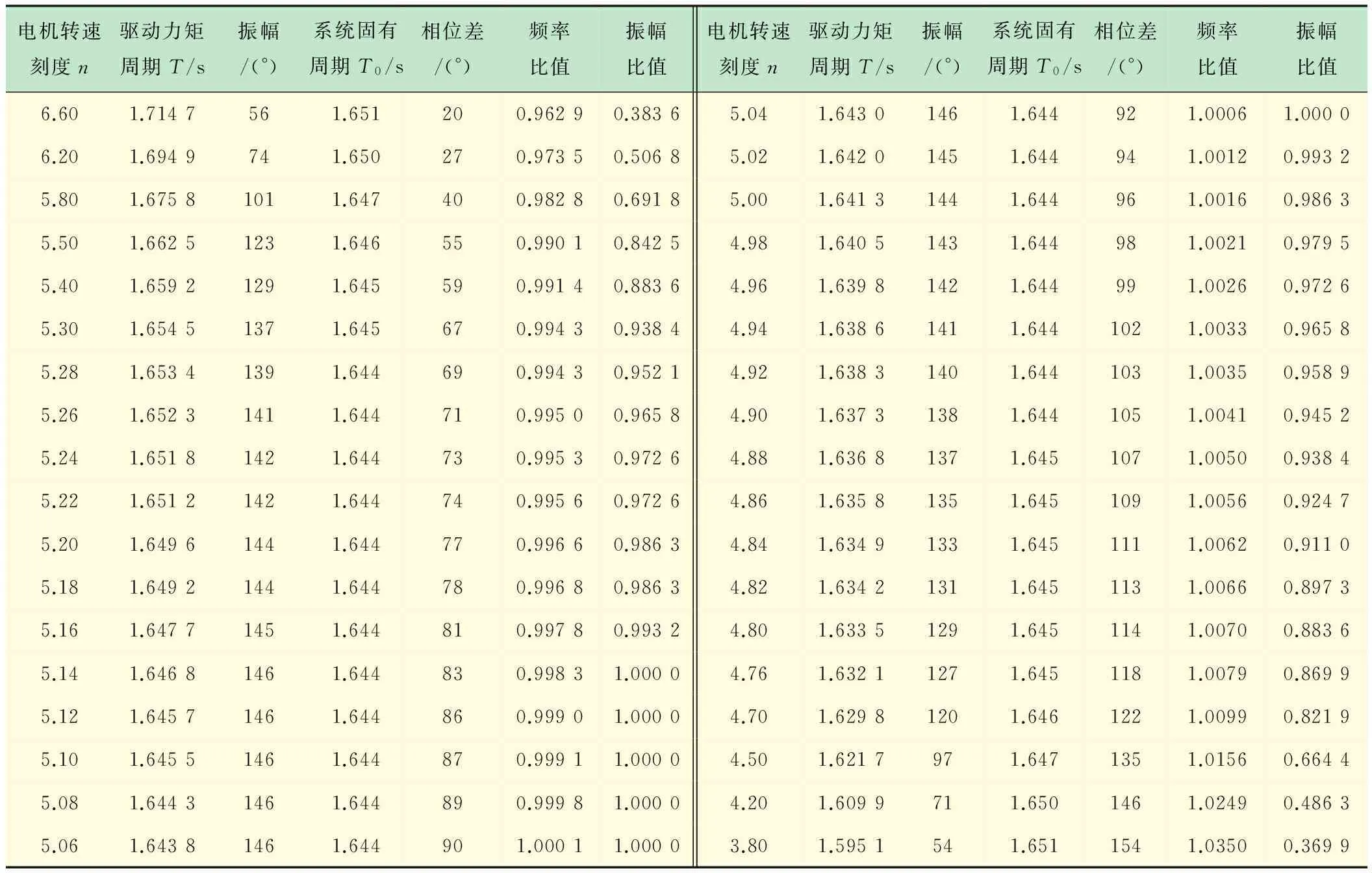
表2 受迫振動的測試數據(阻尼電流旋鈕檔位：1)

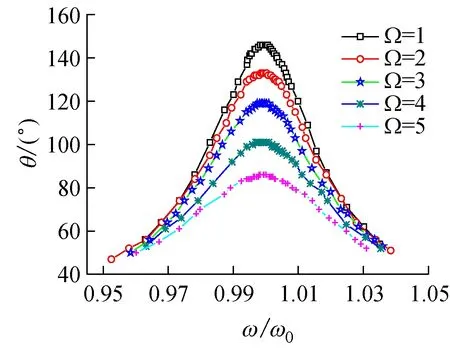
圖1 幅頻特性曲線

圖2描述的是不同阻尼條件下振動系統的相頻特性曲線。可以發現，在擺輪的振動達到穩定狀態時，擺輪的振幅變化與驅動力矩變化非同相位，其相位差隨阻尼系數的增大而使相頻特性曲線變得平坦：當ω/ω0<1時，阻尼系數越大振動的相位差越大；當ω/ω0>1時，阻尼系數越大振動的相位差反而越小。當驅動力矩的角頻率與系統的固有角頻率相同時產生共振，此時振幅最大，相位差為90°。

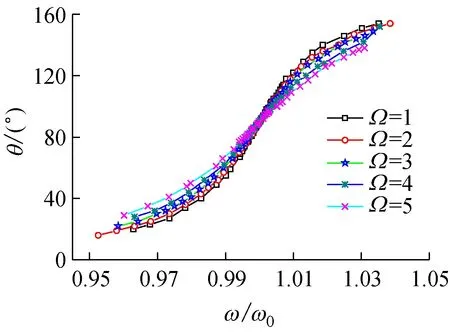
圖2 相頻特性曲線

對于幅頻特性，系統振幅達到極值時與系統耦合的阻尼之間滿足的標度規律如圖3所示。

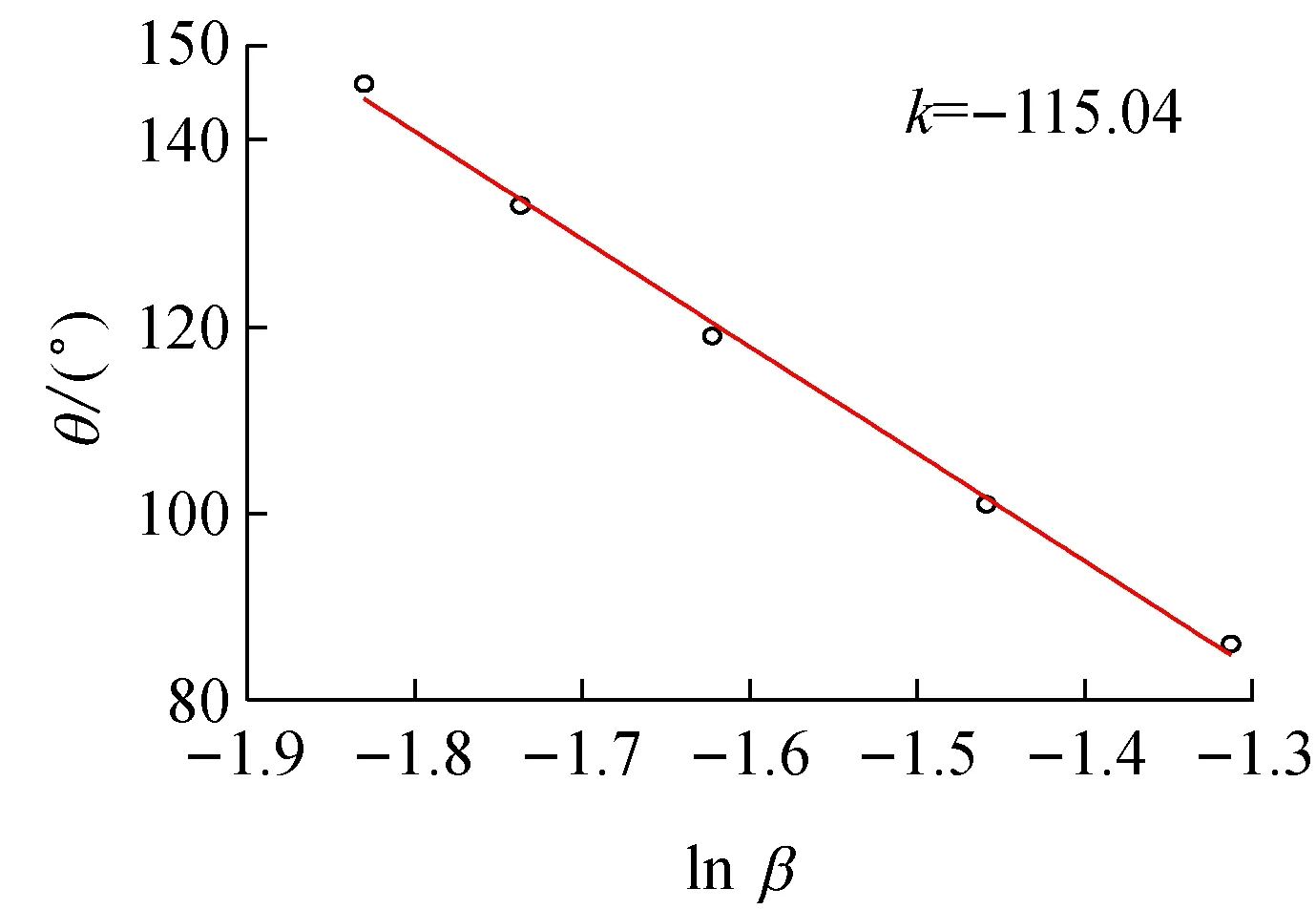
圖3 振幅與阻尼系數成指數標度律

從圖3可以發現，系統的振幅與阻尼系數之間呈指數函數關系，即

(8)

其中，k=-115.04。表明系統的振幅隨系統阻尼系數的增大而呈指數規律衰減。

3 結 語

本文研究了受迫振動系統在多種不同阻尼條件下的幅頻特性和相頻特性，即振動系統的振幅隨ω/ω0的不同而變化。當ω/ω0=1時，振動系統的振幅達到了極大值，即驅動力矩的角頻率與系統的固有角頻率相同時發生共振，且振幅大小與阻尼系數呈負指數規律變化。此外，振動系統在不同阻尼條件下，隨ω/ω0增大，擺輪的振幅與驅動力矩間的相位差也隨著增大，且曲線均在θ=90°處出現了拐點，即相位差在90°附近時，振動系統發生共振。這對減振降噪技術的工程實現可起到一定的理論借鑒作用[18-20]。

[1] [美]湯姆遜 W T.振動理論及其應用[M].胡宗武等譯.北京: 煤炭工業出版社,1980:55-60.

[2] 朱鶴年.新概念基礎物理實驗講義[M].北京: 清華大學出版社,2013:101;136-183.

[3] 周開紅. 共振的條件及特點[J]. 云南師范大學學報(自然科學版)，2011,31(4):69-73.

[4] 馬文蔚,蘇惠惠,解希順. 物理學原理在工程技術的應用[M].3版.北京: 高等教育出版社, 2006: 201-212.

[5] 鄭長聚,洪宗輝,王提賢，等. 環境噪聲控制工程[M].北京:高等教育出版社,1988:150-152, 218-222.

[6] 李慶峰,朱皓月,肖 進，等. 自由活塞式內燃發電機振動特性[J].內燃機學報,2009, 27(4):370-374.

[7] 李萬莉,劉 鵬. 共振梁受迫振動的動力學建模與求解[J].建設機械技術與管理，2014,22 (1):101-103.

[8] 朱鶴年. 波爾共振儀受迫振動的運動方程[J].大學物理, 2006, 25(11): 40-48.

[9] 王 憶,楊玉屏,趙健生.受迫阻尼振動系統動力學性質的研究[J].大學物理,2007, 20(7) :20.

[10] 朱華澤.用波爾共振儀研究受迫振動特性[J].大學物理實驗, 2011, 24(3): 57-60.

[11] 丁 虎,陳立群. 軸向運動黏彈性梁橫向非線性受迫振動[J].振動與沖擊,2009,28(12):128-131.

[12] 方 凱,陳銘南.智能型波爾共振儀網絡系統的設計[J].實驗室研究與探索,2006. 25(7): 771-773

[13] 董 霖,王 涵,朱洪波.波爾共振實驗異常現象的研究[J].大學物理, 2010, 29(2): 57-60

[14] 郎 江.受迫振動實驗中幾個問題的探討[J].大學物理實驗,2013,26(5):55-56.

[15] 陳 思,陳駿逸. 音叉作受迫振動的速度共振幅頻響應曲線的研究[J].實驗技術與管理,2007, 24(12):48-50.

[16] 王 昊,陳立群. 強橫向激勵作用下屈曲梁的穩態幅頻特性[J].應用數學與力學，2014, 35(2):181-187.

[17] 杜全忠,任 曉. 低頻振子相頻特性的分析[J].大學物理實驗, 1998,11(4): 11-14.

[18] 王成會,程建春. 微管內氣泡的受迫振動[J].物理學報,2012,61(19): 194303-1-7.

[19] 舒 蕾. 車削加工中的振動原因分析及消振措施探討[J]. 自動化與儀器儀表，2014(9):142-144.

[20] 程敏熙,肖鳳平,李志為. 從受迫振動到混沌的實驗系統設計[J]. 大學物理，2014, 33(11):34-37.

Research by Forced Vibration of Damping Characteristics

DUQuan-zhong1,WANGPeng2,WANGXu-ming1,YAOMing1

(1.School of physics & Electrical Information Engineering, Ningxia University, Yinchuan 750021, China;2. School of General Studies, Northern University of Nationalities, Yinchuan 750021, China)

To interpret the phenomenon of different damping vibration, we used Boer’s instrument to research the phase-frequency characteristics and amplitude-frequency characteristics with different damping. Coupling system of phase-frequency and amplitude-frequency obtained different curves of characteristics from different position. The characteristic of amplitude-frequency is the single peak of distributed. When the angular-frequency ratio was equal to one, the amplitude-frequency reached extremes and the phase-frequency appeared crossover point. By analyzed the amplitude-frequency of extreme point, we found that the amplitude is depended on damping with the negative exponential power. Furthermore, the displacement by vibration and drive torque change is not the same phase, and the phase difference is equal to 90 degree when the resonance is occurs. The results of this experimental study have a theoretical reference for engineering realization of vibration and noise reduction technology.

damping characteristics; forced vibration; phase-frequency characteristics; amplitude-frequency characteristics

2015-01-15

國家自然科學基金項目(No. 61440050)

杜全忠(1962-),男,寧夏中寧人,副教授,長期從事大學物理實驗教學、實驗技術及實驗項目開發等研究工作。

Tel.:13895016068;E-mail:1341714525@qq.com

O 4-33

A

1006-7167(2015)11-0014-04