負荷相關的風電并網系統線路過載風險控制

路攀，李雪，王春亮

（1．上海大學機電工程與自動化學院，上海 200072；2．河南省中原油田采油一廠注水大隊，濮陽 457000）

風力發電作為新能源中最具有經濟發展前景的一種發電形式，逐漸受到各國的重視并得到廣泛的開發和利用。然而隨著大規模風電接入電網，其隨機性、間歇性和擾動性等特性給電力系統安全運行帶來很大挑戰，常常引起線路過載、電壓越限等事故的發生[1-3]。對線路過載、電壓越限等進行風險控制達到減小系統風險的目的，對電力系統安全穩定與運行具有非常重要的現實意義。

風險控制有多種實現方法。文獻[4-6]提出了用于靜態穩定預防控制的靈敏度方法；文獻[7-9]提出了基于連續線性規劃的靜態穩定預防控制方法；文獻[10]提出了電力系統最優潮流方法，在滿足系統運行和安全穩定約束的特定條件下，通過調整系統中的控制變量來實現預定目標最優的系統穩定運行狀態，該方法有效解決了非線性的優化問題，為電力系統預防控制提供了良好的應用工具；文獻[11]考慮了系統的故障情況，但是沒有考慮故障發生的概率；文獻[12]利用無序遺傳多目標最優化方法，能夠綜合考慮安全性和經濟性；文獻[13]提出了一種風險導向預防控制策略，能夠對線路過載進行預防控制。但是以上文獻都沒有考慮風電接入電網后對系統線路過載風險指標的影響。

大規模風電接入電網后，對電力系統風險控制模型及方法帶來挑戰，負荷、發電機和風電出力的不確定性[13-14]、以及負荷的相關性等，使得假設輸入變量相互獨立的傳統風險控制模型不再適用，有必要研究考慮負荷相關性的風險控制模型，并分析相關性對風險指標的影響。本文建立了以發電成本和線路過載風險指標為目標函數的風險控制模型，基于Cholesky分解法對負荷相關性進行建模，采用跟蹤中心軌跡內點法求解，得到系統的線路過載風險和發電成本值，并分析負荷相關性對線路過載風險指標的影響。

1 線路過載風險指標

1.1 風險的可能性

可能性指標是指當置信水平為r時，隨機變量樣本不滿足安全閾值的累積分布函數，即

式中：Lik（Zi）為可能性指標；Zi為第i條支路線路潮流；Zimin和Zimax分別為第i條支路線路潮流值的下限和上限值；γ為置信水平，當隨機變量的樣本服從“5σ原理”時，可表示為

式中，E（Zi）、D（Zi）分別為Zi的期望和方差。當樣本足夠大時，隨機變量的概率密度函數是連續的，所以累積分布函數可以表述為

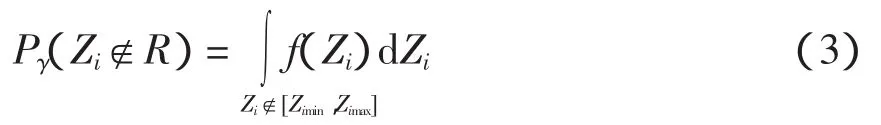
式中，f（Zi）為的概率密度函數。

1.2 風險的嚴重性

線路過載的嚴重性與線路的潮流分布和線路特性有關，流過線路的功率占其額定功率的百分比決定了線路的過載程度，文獻[14]提出了一種分析線路過載嚴重性的方法，線路過載的嚴重度函數如圖1所示。

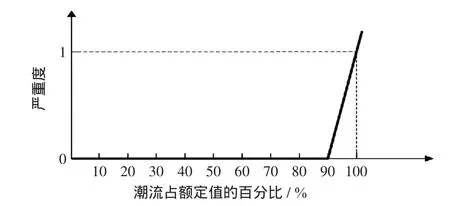
圖1 線路過載的嚴重度函數Fig.1 Gravity function of line overload

1.3 風險指標

基于風險理論和線路過載風險的定義，線路i的過載風險指標risk為線路潮流波動的可能性pr與波動的嚴重性se的乘積，其計算公式為

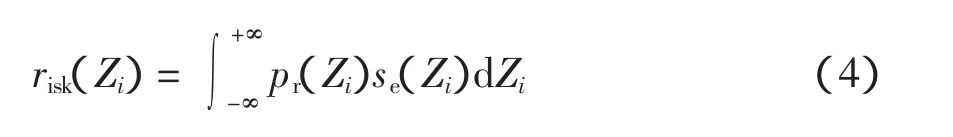
式中，pr（Zi）、se（Zi）和risk（Zi）分別為線路i潮流波動的可能性、嚴重性和過載的風險。

根據累加性，全系統線路過載風險指標rall為

2 線路過載的風險控制

式中：SG為發電機集合；a2i、a1i和a0i為發電成本系數；PG，i為常規機組有功電源出力。

（2）等式約束為

2.1 風險控制模型

發電成本與線路過載風險分別反映系統的運行成本及運行風險。常規的最優潮流計算僅對運行成本進行優化，無法反映由線路潮流波動引起的安全隱患；而僅考慮運行風險進行優化，則無法評價通過控制變量優選后系統的經濟性。因此，本文提出綜合考慮運行成本和運行風險作為優化目標的風險控制模型，兼顧系統的安全性與經濟性，通過調整發電機出力，對發電成本及線路過載風險同時進行優化。具體模型如下。

（1）目標函數為

式中：QG，i為常規機組無功電源出力；PD，i、QD，i分別為有功和無功負荷；Pi（）、Qi（）分別為節點電壓實部e、虛部f及有載調壓變壓器變比t的函數。

（3）風電節點i對應的潮流方程為

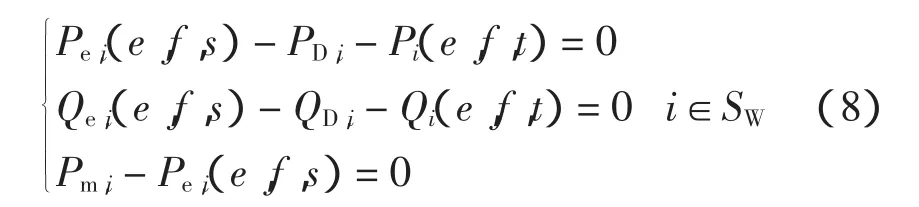
式中：Pm，i為風力機的機械功率；s為異步機的滑差；Pe，i、Qe，i分別為異步發電機發出的有功功率與吸收的無功功率，表達式見文獻[15]。

（4）不等式約束為

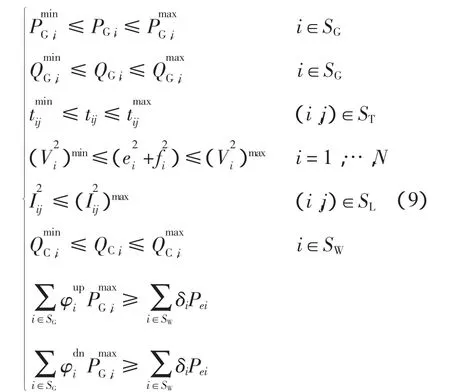
2.2 Cholesky分解方法

具有相關性的輸入變量樣本通過Cholesky分解法生成，其中包括負荷的有功和無功功率。對于電力系統中的一個N維隨機變量M，其協方差矩陣CM表示為

式中，R為一個對稱矩陣，可以通過Cholesky分解法得到[16]，R=LLT，其中L是一個下三角矩陣。假設W為一個相互獨立并且方差為1的N維隨機向量，且

式中，I為單位矩陣。

設M=LW，并且M的協方差矩陣為CM=E（MMT）=E（LMMTLT）=R（12）因此，隨機向量M具有了設定的相關性。具體實現步驟如下：

（1）生成一個相互獨立并且方差為1的N維隨機向量W；

（2）由已知的協方差矩陣R，根據Cholesky分解法得到L矩陣；

（3）根據M=LW，得到具有設定相關性的隨機向量M。

2.3 跟蹤中心軌跡內點法

內點法最初的基本思路是希望尋優迭代過程始終在可行域內進行。但是隨著系統規模的增大，初始點越來越難尋找，因此改進的跟蹤中心軌跡內點法[17，18]只要求在尋優過程中松弛變量和拉格朗日乘子滿足簡單的大于零或者小于零的條件，使計算過程大為簡化。具體過程見下：

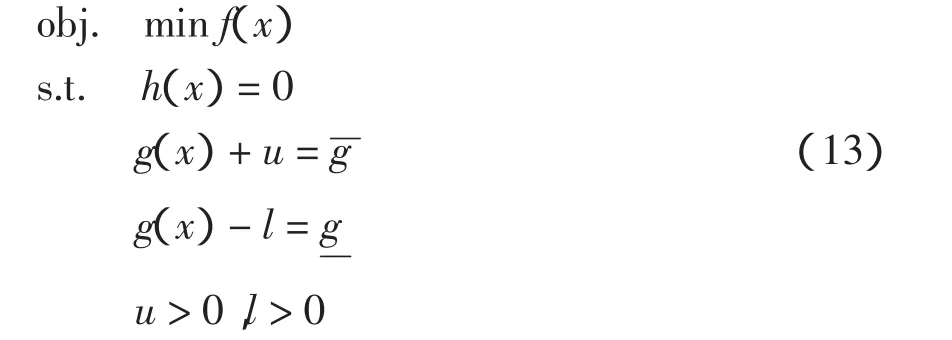
式中：μ為障礙常數[18]；y、z和w分別為等式和不等式約束的拉格朗日乘子。式（14）極小值的必要條件是拉格朗日函數L對所有變量及乘子的偏導數為0。

3 算例分析

圖2為風電機組接入IEEE-14節點系統，等值后的風電機組經升壓變壓器接入IEEE-14節點系統的14號節點。對該系統，利用Matlab編寫程序代碼，利用蒙特卡洛模擬方法求解包含不確定變量并考慮負荷相關性的過載風險控制問題。風電場詳細參數見文獻[15]。

假設功率的基準值為100 MVA，風速服從Weibull分布，其分布參數為k=10.7，c=6.289 2，母線電壓的上下界分別為1.10和0.95，發電機參數見表1。

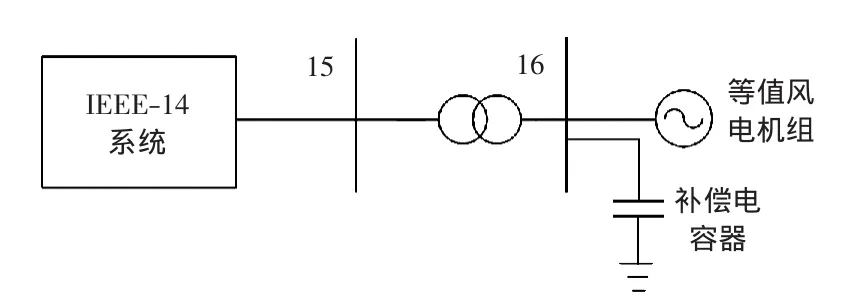
圖2 含風電場的IEEE-14節點系統Fig.2 IEEE 14-bus system connected with wind farms

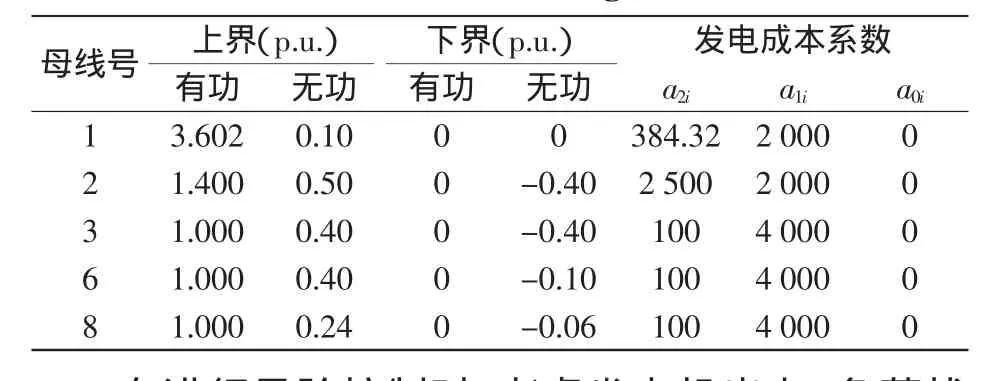
表1 發電機參數Tab.1 Parameters of generator

在進行風險控制時，考慮發電機出力、負荷擾動和風速的隨機性。并在假設負荷相互獨立和相關2種情形下進行仿真。經過線路過載風險控制后，2種情形下的線路過載風險值見表2。控制前后2種情形下的總成本和總風險值見表3。

表2 線路過載風險值Tab.2 Overload risk value of lines

從表2可知，考慮負荷相互獨立和相關2種情形下，各個線路的風險值均呈現不同程度的改變，個別線路風險值差異比較突出。例如線路4-5，負荷相關時風險值為0.226 4，獨立時為0.189 2，表明負荷相關性對線路過載風險值產生影響。

從表3可知，在負荷相互獨立時，通過對發電機出力進行調整，進行風險控制后系統的運行成本增加了2.4%，而線路過載風險減少了11.4%；負荷互相關時，控制后運行成本增加了2.1%，而線路過載風險卻減少了13.2%。表明通過風險控制，增加了少量的系統運行成本，但大大減少了運行風險。但無論控制前還是控制后負荷相關和獨立兩種情形下的系統總費用和總風險值也存在差異，表明相關性會對系統過載風險值和運行成本產生影響，在進行過載風險預防控制時應該考慮負荷之間的相關性。

表3 系統運行成本和過載風險值Tab.3 Total cost and overload risk value of system

4 結語

本文在考慮風速、發電機出力負荷不確定性以及負荷相關性的基礎上，提出了考慮相關性的風電并網系統線路過載風險控制問題；采用Cholesky分解法對相關性進行建模，以系統運行成本和過載風險指標為目標函數建立風險控制模型。算例結果表明，負荷之間的相關性會對發電機有功功率和無功功率產生影響，同時也會影響到系統運行成本和過載風險值。因此在進行風險控制時應該考慮負荷之間的相關性。

[1]張良棟，石輝，張勇軍（Zhang Liangdong，ShiHui，Zhang Yongjun）.電網事故原因分類淺析及其預防策略（Analysis of cause and prevention methods for power network accidents）[J].電力系統保護與控制（Power System Protection and Control），2010，38（4）：130-133，150.

[2]陳亦平，洪軍（Chen Yiping，Hong Jun）.巴西“11·10”大停電原因分析及對我國南方電網的啟示（Analysis on causes of blackout occurred in Brazilian power grid on Nov.11，2009 and lessons drawn from it to China southern power grid）[J].電網技術（Power System Technology），2010，34（5）：77-82.

[3]Amew.Power system operation corporation limited[R].New Delhi：National Load Despatch Centre，2012.

[4]Greene S，Dobson I，Alvarado F L.Sensitivity of loading margin to voltage collapse with respect to arbitrary parameters[J].IEEE Trans on Power Systems，1997，12（1）：262-272.

[5]Greene S，Dobson I，Alvarado F L.Sensitivity of transfer capability margins with a fast formula[J].IEEE Trans on Power Systems，2002，17（1）：34-40.

[6]李海濤，孫聞，趙兵，等（LiHaitao，SunWen，Zhao Bing，et al）．基于交流靈敏度的在線安全控制策略（Online security control analysis based on sensitivity method）[J]．電力系統及其自動化學報（Proceedings of the CSU-EPSA），2012，24（1）：32-36．

[7]Feng Zhihong，Ajjarapu V，Maratukulam D J.A comprehensive approach for preventive and corrective control to mitigate voltage collapse[J].IEEE Trans on Power Systems，2000，15（2）：791-797.

[8]Capitaneseu F，Van’Cutsern T.Preventive control of volt-age security margins：a multicontingency sensitivitybased approach[J].IEEE Trans on Power Systems，2002，17（2）：358-364.

[9]Wu Q，Popovic DH，HillD J，et al.Voltage security enhancementvia coordinated control[J].IEEE Trans on Power Systems，2001，16（1）：127-135.

[10]Carpentier J.Coniribution a l’etude du dispatching economique[J].Bulletin de la Societe Francaise des Eleetrieients，1962，3（1）：431-447.

[11]Song Hwachang，Lee Byongjun，Kwon Sae-hyuk，et al.Reactive reserve-based contingency constrained optimal power flow（RCCOPF）for enhancement of voltage stability margins[J].IEEE Transon Power Systems，2003，18（4）：1538-1546.

[12]Xiao Fei，McCalley JD.Power system risk assessment and control in a multiobjective framework[J].IEEE Trans on Power Systems，2009，24（1）：78-85.

[13]Wen Y F，Wang Y，Guo CX，et al.Risk-oriented preventive control of transmission lines overload[C]//IEEE Power and Energy Society General Meeting.San Diego，USA，2012.

[14]NiMing，McCalley JD，Vittal V，et al.Online risk-based security assessment[J].IEEE Trans on Power Systems，2003，18（1）：258-265.

[15]LiXue，Cao Jia，Du Dajun.Two-point estimate method for probabilistic optimal power flow computation including wind farms with correlated parameters[J].Communications in Computer and Information Science，2013，355：417-423.

[16]Morales JM，Conejo A J，Perez-Ruiz J.Simulating the impact of wind production on locational marginal prices[J].IEEE Transon Power Systems，2011，26（2）：820-828.

[17]王錫凡.現代電力系統分析[M].北京：科技出版社，2011.

[18]Jiang Quanyuan，Geng Guangchao，Guo Chuangxin，et al.An efficient implementation of automatic differentiation in interior point optimal power flow[J].IEEE Trans on Power Systems，2010，25（1）：147-155.