混合網格方法研究柵格翼亞跨超聲速氣動特性

涂正光，梁紀秋，周 錚

(中國航天科工集團第九總體設計部，湖北武漢 430040)

混合網格方法研究柵格翼亞跨超聲速氣動特性

涂正光*，梁紀秋，周 錚

(中國航天科工集團第九總體設計部，湖北武漢 430040)

采用基于結構/非結構混合網格的CFD方法對柵格翼的亞跨聲速氣動特性進行了研究，計算方法經過試驗數據的驗證，可達到工程精度。對單獨柵格翼的研究表明，跨聲速壅塞時，流動通過柵格前方亞聲速氣流減速從柵格外側溢流而實現流量調節;超聲速壅塞時，流動通過在柵格翼上產生網狀脫體激波使來流減速至亞聲速來進行流量調節，且計算結果與理論估算上下臨界馬赫數范圍一致。對某柵格翼氣動布局導彈的計算結果表明，在跨聲速壅塞區間內，壅塞有自我調節作用，通過溢流使柵格通道內維持相似流動，從而使柵格氣動性能保持基本平穩;同時由于溢流使流量下降，柵格翼升力效率下降，導彈靜穩定性減弱。

計算流體力學;柵格翼;混合網格;壅塞

0 引 言

柵格翼［1］是一種特殊的氣動構件，由小弦長的框架及在其內部交叉放置的細薄翼面構成。與傳統平板翼面相比，柵格翼將升力面由平面分布發展為空間分布，布局更為緊湊，因此具有鉸鏈力矩小、升力特性優良、結構承力合理等特性。柵格翼研究在航空航天領域日益得到重視［2］。前蘇聯在20世紀50年代開始研究柵格翼，柵格翼的應用最為廣泛，除了“聯盟號”飛船以外，在空空導彈、洲際彈道導彈等廣泛的領域都得到了應用。西方國家關于柵格翼的研究工作是從20世紀80年代中后期開始的。美國陸軍航空兵與導彈司令部研究發展與工程中心從1985年到1997年通過9項風洞試驗對柵格翼布局導彈的氣動特性進行了廣泛研究，內容包括基本性能研究、作為控制舵面氣動特性、減阻技術、參數影響分析、飛行器應用、滾轉阻尼研究、隔板和彈體的影響等。試驗馬赫數0.3～3.5，共涉及外形26種，其研究外形BOAR (火箭發射BAT反坦克彈)彈頭已進行了兩次飛行試驗和一次掛機投放飛行試驗。國內在神舟號飛船逃逸艙上也進行了應用，并參加了神舟1號到神舟7號飛船任務［3］。

早期柵格翼空氣動力特性的研究以風洞試驗和工程估算為主。近十幾年來，隨著計算機和計算技術的飛速發展，計算流體力學(CFD)已成為工程設計的有力手段。CFD技術在柵格翼氣動特性研究上的主要難點是:對于柵格翼的蜂窩式結構，多組翼片交錯排列，傳統的分區結構網格技術建模十分困難、生成的網格規模龐大。重疊網格［3］、混合網格［4］的技術發展，為柵格翼氣動特性數值模擬提供了較好的解決方案。

本文采用結構/非結構混合網格方法，研究了某柵格翼氣動布局，對典型狀態流場和氣動性能進行了分析，并且對跨聲速狀態下的柵格壅塞現象進行了解釋，數值計算情況與風洞試驗研究結果一致。

1 柵格翼氣動特性

柵格翼的空氣動力學特性依賴于來流條件和柵格幾何參數(如圖1所示)。一般認為，當來流從亞聲速到超聲速變化時，存在三個特征馬赫數，當氣流在柵格某截面達到聲速進而出現正激波時，伴隨阻力增大，稱第一臨界馬赫數(圖1a)。隨馬赫數增大至超過聲速的某值時，通道內正激波前移并脫體，使升力減小、阻力增大。馬赫數繼續增大，激波逐漸向柵格前緣靠近，至附體時稱第二臨界馬赫數(圖1b)。此后柵格內出現多次反射的斜激波系，當馬赫數增至第三臨界馬赫數(圖1d)，無反射激波，此后柵格舵的流動特性不再出現實質性的變化［6］。

亞聲速柵格(來流小于第一臨界馬赫數)和超聲速柵格(來流大于第二臨界馬赫數)具有良好的空氣動力線性特征，也是人們研究較多的情況。文獻［7］將亞聲速柵格看做一個空間分布的離散附著渦系和自由渦系的升力面系統，采用渦格法作工程估計。文獻［8］采用超聲速薄翼理論計算來流大于第三臨界馬赫數的情況，并對第二臨界馬赫數到第三臨界馬赫數時柵格間存在波系干擾的情況進行修正，獲得較好結果。

圖1 柵格流動狀態Fig.1 Grid fin flow regimes

跨聲速柵格(來流介于第一、二臨界馬赫數之間)流動狀態遠較其它兩種情況復雜，由于通過柵格的氣流受壁面約束明顯，存在跨聲速壅塞問題。由壅塞的定義，在通道流動中任一截面單位時間內流過的質量流量守恒。由于表征熱力學參量的密度和表征運動學參量的流速總成反變關系，流體在亞聲速和超聲速時壓縮性強弱不同，使質量流量密度隨流速增加呈先增后減趨勢，在聲速時存在拐點，有最大值。對于收縮-擴張通道，在最小截面即喉道處達到聲速，能獲得喉道處允許通過的最大質量流量，若進口處流量大于這個值，多余的流體無法通過喉道，即發生了壅塞。文獻［9］指出，在跨聲速臨界馬赫數附近，柵格翼上出現網狀激波和流動壅塞現象，使俯仰力矩和法向力發生劇烈變化，從而導致動態特性變差。

如果流動通道收縮主要由柵格格片厚度引起，可以采用一維等熵流關系式估計柵格進入壅塞狀態的臨界馬赫數，參見式(1)。等熵流關系式在數學上有大于1和小于1的兩個解，對應的物理現象為超聲速氣流和亞聲速氣流分別可以通過收縮通道達到聲速。因此壅塞問題應存在兩個臨界馬赫數，亞聲速解表示柵格進入壅塞的下臨界狀態，超聲速解表示柵格退出壅塞狀態的上臨界狀態［10-11］。

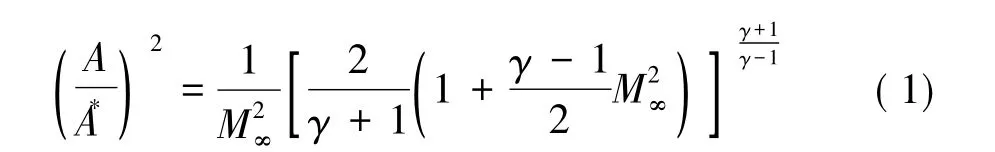
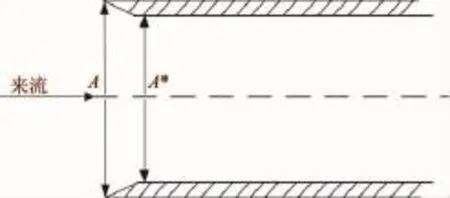
圖2 柵格中面積比Fig.2 Area ratio of grid fin

2 計算方法

2.1 混合網格

高質量的網格生成是CFD研究的關鍵因素。對柵格翼外形，由于多組翼片交錯排列，采用分區結構網格技術拓撲劃分極為困難，即使勉強生成也會出現網格量大、網格質量差等問題。文獻［12］采用非結構網格研究柵格翼，非結構網格由于摒棄了網格節點的結構性限制，具有很強的幾何靈活性，易于生成復雜外形網格，但缺點是存儲和計算效率低，粘性模擬能力差。

為揚長避短，結合結構網格和非結構網格各自的優缺點，人們提出了混合網格的思想。混合網格方法包括:三棱柱/四面體混合網格［13］、四面體/三棱柱/金字塔/六面體混合網格［14］、笛卡爾/四面體混合網格［15］和笛卡爾/四面體/三棱柱混合網格［16］等。

本文采用的混合方法是先對彈體和柵格翼分別獨立生成互不相交的結構網格子塊，各子塊網格采用非結構網格進行填充，滿足非結構網格和結構網格交接面的完全對接。當改變柵格翼的舵偏角時候，彈身和柵格翼上的結構網格保持不變，只需要重新自動生成填充部分的非結構網格。這種混合網格結構能較好處理柵格翼偏轉、任意柵格翼組合等復雜工況，簡化了網格生成難度、有效減少了網格生成人工工作量。

2.2 求解器

本文算例均求解雷諾平均NS方程，空間離散采用Roe的FDS格式，MUSCL插值方法和Van Albada限制器用于獲得二階空間離散精度;湍流模型采用SST模型;時間離散采用穩定性高的LU-SGS隱式計算方法。關于數值方法的詳細介紹參見文獻［17］。

3 計算模型

研究的某柵格翼氣動布局外形彈體由冪次曲線形頭部和圓柱后體組成，4片柵格尾翼呈十字布置。圖3、圖4是網格示意圖，彈體和柵格翼分別生成貼體結構網格，彈體網格數目為176.65萬，單個柵格翼為142.16萬。填充的非結構網格數目約237萬。

4 氣動特性研究

4.1 亞、超聲速特性研究

圖5是單獨一組柵格在亞聲速條件下流場等馬赫數云圖和壓力云圖。在亞聲速來流下，氣流能從柵格順暢通過，柵格對來流作用相當于薄物體擾動，格片前緣肩部處氣流加速作用明顯。在柵格通道內部，由于亞聲速氣流壓縮后熱力學參數減小、動力學參數增大，故通道內氣流相對未擾動氣流，壓力稍低而馬赫數略高。

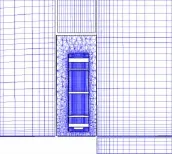
圖3 柵格翼縱截面混合網格Fig.3 Longitudinal section hybrid grid

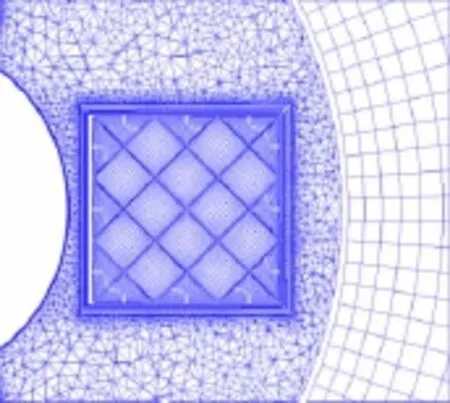
圖4 柵格翼橫截面混合網格Fig.4 Cross section hybrid grid

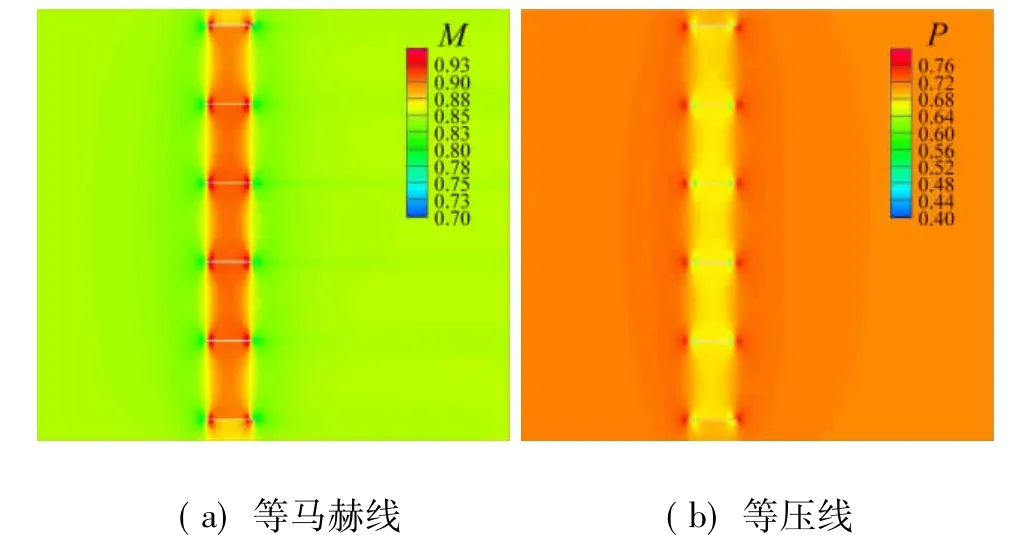
圖5 Ma=0.85柵格流場圖Fig.5 Ma=0.85 grid fin flow field

圖6是單獨一組柵格在超聲速條件下流場等馬赫數云圖和壓力云圖，可以看到當來流馬赫數介于第二臨界馬赫數和第三臨界馬赫數之間時，柵格前緣斜激波系角度較大，激波在相鄰柵格間發生相交、反射，并在通道內產生弱的壓縮波系和膨脹波系，以及結尾激波。

對第3節所述柵格翼氣動布局導彈在超聲速流動下，開展了不同控制舵偏條件的常規風洞測力試驗。圖7給出了部分工況下風洞試驗數據和混合網格計算結果的比較情況。由圖7可以看出，計算結果與試驗符合較好，數據曲線能正確反映氣動性能規律，其中軸向力系數誤差小于15%，法向力系數和俯仰力矩系數符合較好，證明對柵格翼一類復雜氣動構型，本文采用的混合網格方法達到了工程精度。

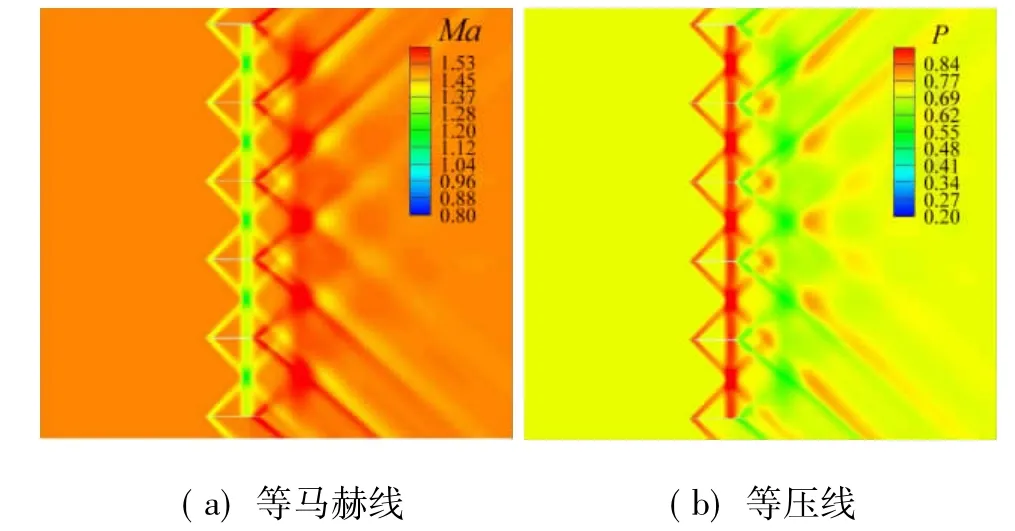
圖6 Ma=1.5柵格流場圖Fig.6 Ma=1.5 grid fin flow field

圖7 CFD和風洞試驗數據比較(Ma=2.5，=0°)Fig.7 Comparison of CFD and wind tunnel(Ma=2.5，=0°)

4.2 跨聲速流場特性

圖8～圖10是單獨一組柵格在跨聲速條件下流場等馬赫數云圖和壓力云圖。當來流馬赫數接近1時，通道內氣流出現壅塞，多余流量對入口前流動產生反饋，入口處馬赫數等值線逐漸密集，亞聲速來流減速，流管擴張，部分流量從柵格外側溢流。圖8中馬赫數0.95時，在格片楔面與腹板轉折處邊緣氣流發生擴張先達到超聲速，并引射出膨脹波系，使中心區域氣流加速至超聲速流動，同時在通道末端出現結尾激波。當馬赫數繼續提高時，結尾激波將經后楔面膨脹與尾跡區壓縮后，形成尾跡激波。

按一維理論，來流馬赫數小于1時，柵格通道經前部楔面壓縮不應出現超聲速流動，三維情況是邊緣氣流先達到超聲速，并使中心區域加速至超聲速，反映了三維與一維問題的不同。壅塞導致的流量過剩，通過柵格前方亞聲速氣流減速擴張，部分流量從柵格外側溢流而實現調節。

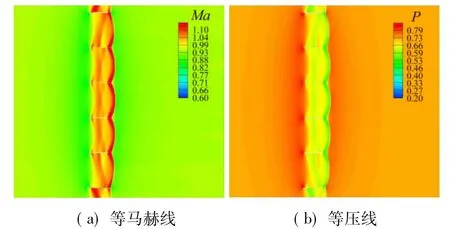
圖8 Ma=0.95柵格流場圖Fig.8 Ma=0.95 grid fin flow field

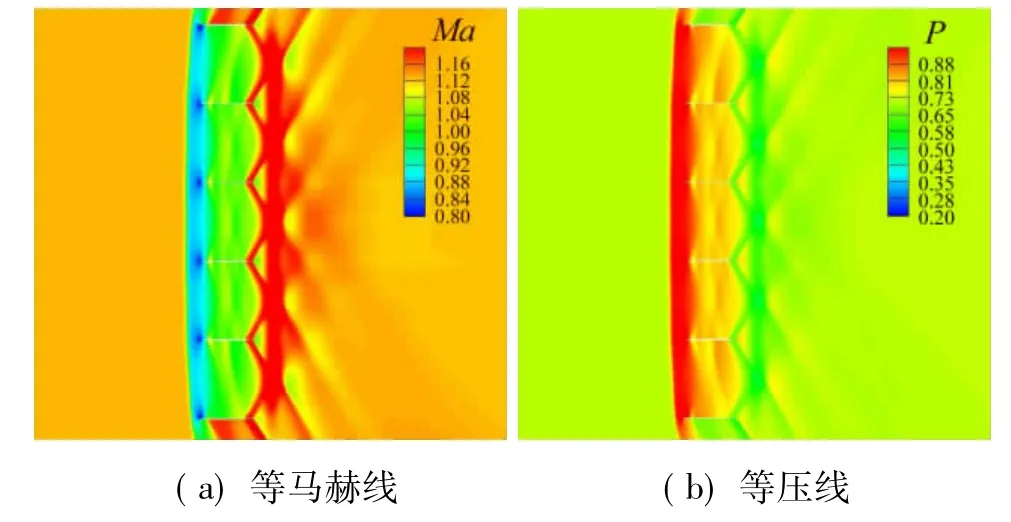
圖9 Ma=1.13柵格流場圖Fig.9 Ma=1.13 grid fin flow field

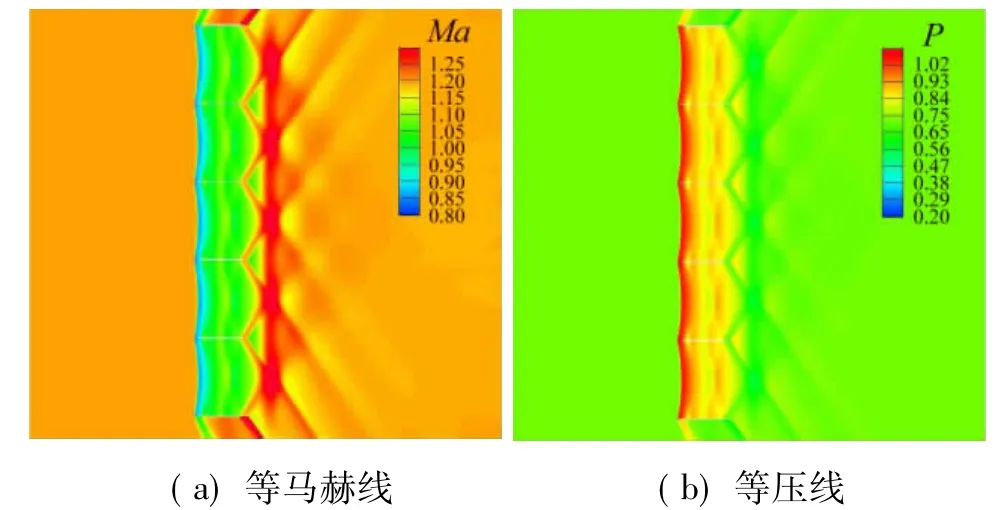
圖10 Ma=1.2柵格流場圖Fig.10 Ma=1.2 grid fin flow field

當來流大于1時，由于超聲速氣流“禁訊原理”，無法以擾動形式平緩地調整流量，而是通過激波改變入口流速和壓力。此時柵格翼前方出現弱的網狀脫體激波(如圖9所示)，同時由于外部流場條件達到超聲速，柵格翼后部的結尾激波消失。隨馬赫數提高，網狀脫體激波逐漸向柵格翼靠近，當大于壅塞的上臨界馬赫數時，超聲速氣流能通過收縮通道，此時激波被吸附在柵格前緣上，如圖10所示。

4.3 跨聲速氣動性能

柵格由下臨界馬赫數進入壅塞后，在來流馬赫數達到上臨界前，將一直維持壅塞狀態。由于上、下臨界馬赫數區間很窄，同時風洞試驗存在雷諾數模擬不準的問題，因此只能通過數值計算在該區間加密來研究柵格翼的跨聲速特性。事實上，文獻［9］也指出，柵格翼跨聲速壅塞只在數值模擬中出現，而風洞試驗中無法復現。因此通過CFD開展了柵格翼在跨聲速附件流動特性的研究。

為便于分析和比較，首先選取了一組柵格格片和單獨一個格片(如圖11所示)進行對比研究。圖12是柵格格片和單格片在不同馬赫數下氣動性能比較，兩者軸向力系數隨馬赫數均呈單峰變化趨勢，但法向力系數有較大差異。低馬赫速時柵格格片法向力系數小于單格片，柵格通道對格片的壁面約束類似于兩個“氣墊”，使法向力變化更加平緩，這也是柵格翼在大攻角時不易失速的原因。柵格進入壅塞狀態后，法向力系數急劇下降，直至退出壅塞時法向力系數回升，其間呈現一個變化平緩的凹坑形狀，即壅塞區間柵格氣動性能出現大幅度下降。

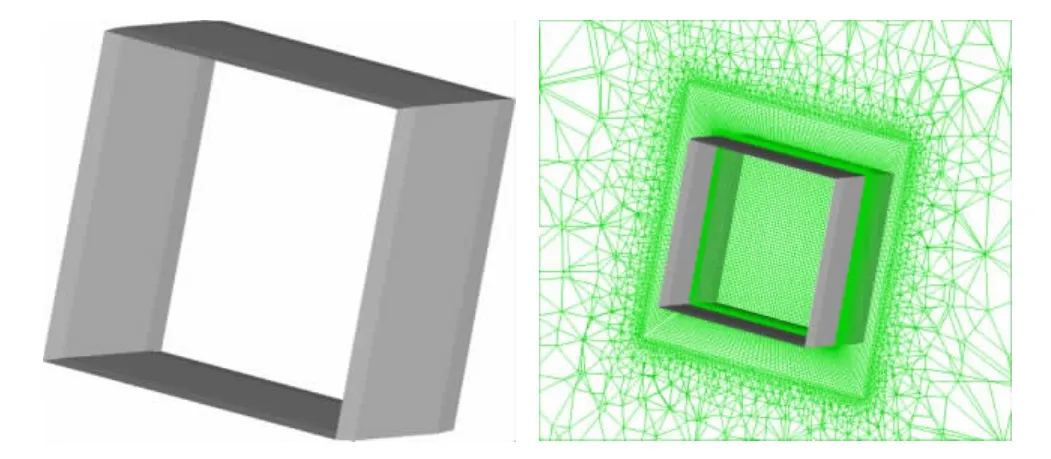
圖11 單柵格及其混合網格Fig.11 Single fin and hybrid grid

圖13給出了混合網格計算的柵格翼布局導彈的翼面氣動性能，參數變化趨勢與圖12中一組柵格格片的規律一致。CN在馬赫數0.9～1.2之間出現一個凹坑。結合前述流場分析可知，壅塞起一種自我調節的作用，通過溢流使通道內維持相似流動，使氣動性能相對單格片的劇烈變化能保持平穩。但同時也是因為溢流使流量下降，柵格翼升力效率有較大減少，使全彈氣動布局穩定性下降。

針對所研究的柵格翼，下臨界馬赫數為0.8869，上臨界馬赫數為1.1206。圖14給出了下臨界馬赫數以下、上臨界馬赫數以上及其間三個典型馬赫數的單個柵格內的流動圖畫。圖15為質量流密度隨馬赫數的變化。由流動圖畫、質量流密度變化曲線可見，CFD計算結果與理論分析一致。

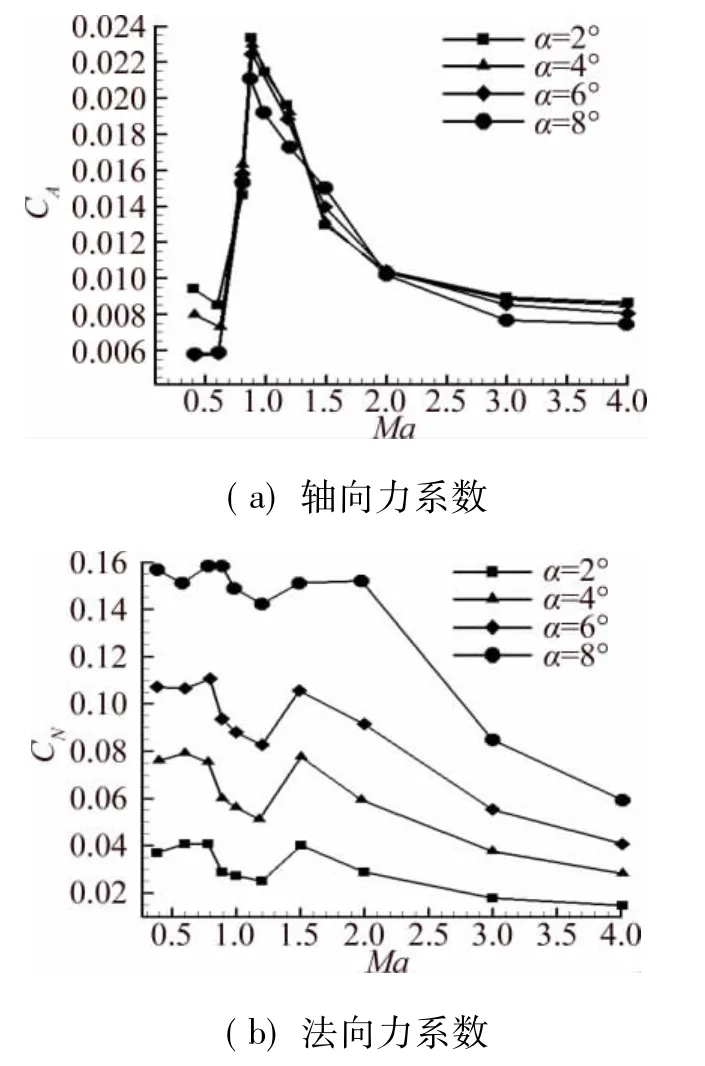
圖13 柵格翼布局導彈翼面氣動性能Fig.13 Grid fin aerodynamic characteristics of one missile

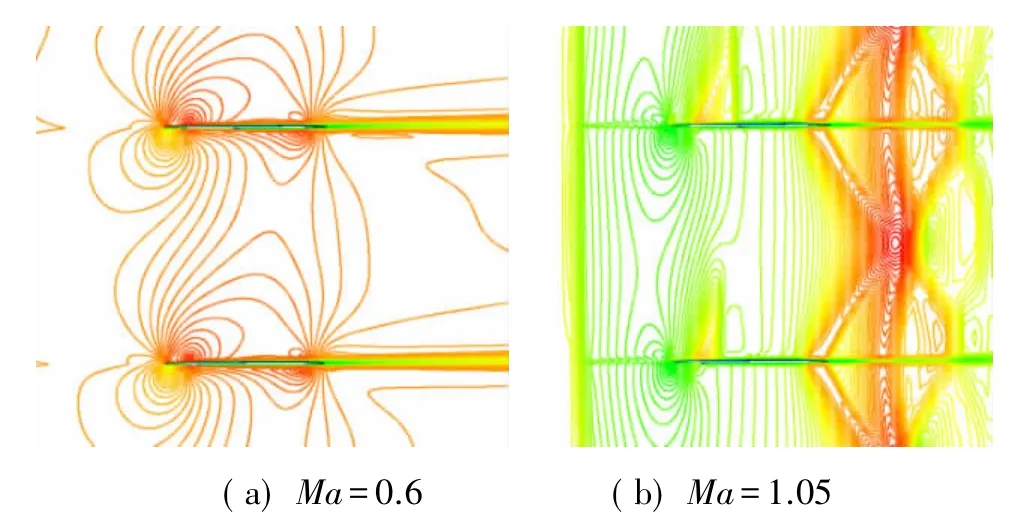
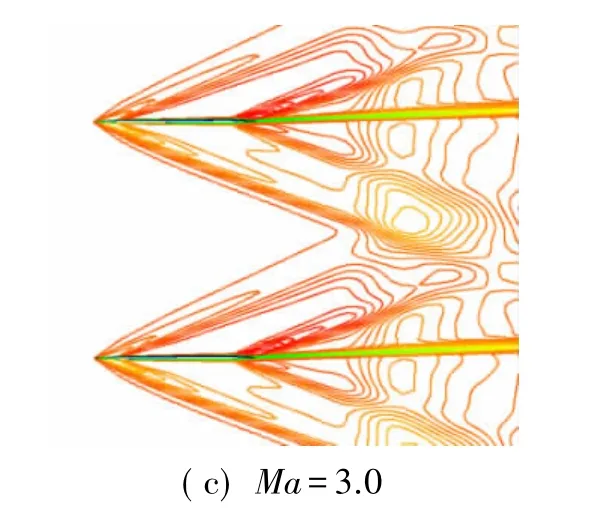
圖14 單個柵格內的等馬赫線Fig.14 Mach contours of single fin

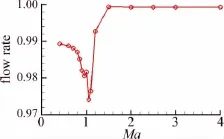
圖15 質量流密度隨馬赫數的變化Fig.15 Mass flow rate changing with Ma

5 結 論

本文采用結構/非結構混合網格方法對柵格翼外形進行了研究，與風洞試驗數據進行對比，驗證了計算方法的正確性。主要結論有:

(1)通過對柵格翼在亞跨超聲速范圍內典型流動狀態進行的分析，重點解釋了跨聲速區柵格壅塞特性，指出壅塞導致的流量過剩，通過柵格前方亞聲速氣流減速擴張，部分流量從柵格外側溢流而實現調節，超聲速壅塞時，柵格翼上將產生網狀脫體激波使來流減速再進行調節;

(2)由一維理論計算的上、下臨界馬赫數，分別對應柵格翼進入、退出壅塞的臨界點，估算值與數值模擬結果符合較好;

(3)柵格翼進入壅塞區間后，由于流量下降，升力效率有較大減少，使氣動布局穩定性下降。但由于壅塞的自調節作用，流動形態較為穩定，在壅塞區間內能保持氣動特性的平緩變化。

［1］ 貝洛齊爾科夫斯基.柵格翼［M］.中國運載火箭技術研究院，譯.1994.

［2］ Li H H，Shi Y H.Current status and development trend of grid fin［J］.Missile and Space Vehicle，2008，(6):27-30.(in Chinese)黎漢華，石玉紅.柵格翼國內外研究現狀及發展趨勢［J］.導彈與航天運載技術，2008，(6):27-30.

［3］ Cai Q Y，Ni J M.The aerodynamic simulation of max dynamic head test for the lattice wing of escape rocket［C］//Proceedings of the 1st National Conference on Mechanical Problems in the Field of Aerospace，2004:7-10.(in Chinese)

蔡巧言，倪嘉敏.逃逸飛行器柵格翼最大速度頭試驗的氣動模擬［C］.首屆全國航空航天領域中的力學問題學術研討會，2004:7-10.

［4］Fan J J.Complex overlapping grid method and multi-body movement of the unsteady flow dynamic simulation［D］.Beijing:Beihang University，2010.(in Chinese)

范晶晶.復雜重疊網格方法研究及多體運動的非定常流動模擬［D］.北京:北京航空航天大學，2010.

［5］ Liu G，Xiao Z Y，Jiang X，et al.Flow simulation of missile with grid fins using structured-unstructured hybrid grids［J］.Acta Aerodynamica Sinica，2007，25(2):277-280.(in Chinese)

劉剛，肖中云，江雄，等.混合網格方法在柵格翼數值模擬中的應用研究［J］.空氣動力學學報，2007，25(2):277-280.

［6］ Przemieniecki J S.Tactical missile design［M］.AIAA 2001.

［7］ Zhu Z X，Xu M.The aerodynamic calculation and analysis of subsonic grid fins［J］.Tactical Missile Technology，1998，(1):10-16.(in Chinese)

朱戰霞，徐敏.亞聲速柵格翼氣動計算與分析［J］.戰術導彈技術，1998，(1):10-16.

［8］ Xu M，Zhu Z X.Analysis of supersonic aerodynamic characteristics on grid fins［J］.Tactical missile technology，1999，(1):1-6.(in Chinese)

徐敏，朱戰霞.超聲速柵格翼空氣動力特性計算與分析［J］.戰術導彈技術，1999，(1):1-6.

［9］ Montgomery C H，Eric L B.Transonic aerodynamic analysis of lattice grid tail fin missiles［R］.AIAA 2006-3651，2006.

［10］ Karl O.Aerodynamic analysis of lattice grid fins in transonic flow［D］.Ohio:Department of the Air Force Air University，2004.

［11］Anderson J D.Modern compressible flow:with historical perspective［M］.New York:McGraw-Hill Companies Inc.2003.

［12］James D，Harris L E.CFD analysis of grid fins for maneuvering missiles［R］.AIAA2000-0391，2000.

［13］Kallinderis Y，Khawaja A，Mcmorris H.Hybrid pris-matic/tetraheral grid generation for complex geometries［J］.AIAA J.，1996，34: 291-298.

［14］Coirier WJ，Jorgenson PCE.A mixed volume grid approach for the Euler and Navier-Stokes equations［R］.AIAA Paper 96-0762，1996.

［15］Zhang L P，Zhang H X，Gao S C.A cartesian/unstrutured hybrid grid solver and its application to 2D/3D complex inviscid flow fields［C］//ZHUANG F G，edited.Proceedings of the 7th International Symposium on CFD.Beijing，China:International Academic Publish-ers，1997:68-83.

［16］Zhang L P，Yang Y J，Zhang H X.Numerical simulations of 3D inviscid/viscous flow fields on cartesian/unstructured/prismatic hybrid grids［C］//ZHANG H X，edited.Proceedings of the 4th Asian CFD Conference.Mianyang，China:University of Electronic Science and Technology of China Press，2000:93-103.

［17］ Yan C.Methods and application of computational fluid dynamics［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2006:245-248.(in Chinese)

閻超.計算流體力學方法及應用［M］.北京:北京航空航天大學出版社，2006:245-248.

Research on the aerodynamic characteristics of grid fin by hybrid grid method

Tu Zhengguang*，Liang Jiqiu，Zhou Zheng
(The 9th Designing of China Aerospace Science Industry Corp.，Wuhan Hubei 430040，China)

The aerodynamic characteristics of the grid fin are studied by employing CFD approach based on structured/unstructured hybrid mesh technique.The computational method is validated by the wind tunnel measurements to attain engineering accuracy.The research on one single grid fin indicates that，in the case of transonic choking，the coming subsonic airstream forward of the grid fin goes around its outer edge to achieve the mass flux adjusting，while in the case of supersonic choking，the coming supersonic flow is decreased to subsonic by the web-shaped detached shock waves produced by the grid fin and then the mass flux is adjusted，the computed results are in agreement with the range of upper and lower critical Mach numbers predicted by the theoretical estimations.The computational results show that，once the transonic flow past the grid fin presents choking phenomenon，the choking has a self-adjusting effect，which sustains a similar flow in the flow passage of the grid fin through outflowing and then preserve the aerodynamic characteristics essentrially steady;and for the decrease of mass flux，the lift efficiency drops and the static stability of the missile also decreases.

computational fluid fynamics(CFD);grid fin;hybrid grid;choked flow

V211.3;V224

A

10.7638/kqdlxxb-2013.0077

0258-1825(2015)03-0427-06

2013-07-17;

2014-07-01

涂正光*(1979-)，湖北英山縣人，研究員，主要研究方向:氣動布局設計.E-mail:can_tu1316@sina.com

涂正光，梁紀秋，周錚.混合網格方法研究柵格翼亞跨超聲速氣動特性［J］.空氣動力學學報，2015，33(2):427-432.

10.7638/kqdlxxb-2013.0077 Tu Z G，Liang J Q，Zhou Z.Research on the aerodynamic characteristics of lattice fin by hybrid grid method［J］.Acta Aerodynamica Sinica，2015，33(2):427-432.