矩形高層建筑平均風壓的風洞阻塞效應試驗研究

黃 劍，顧 明

(同濟大學土木工程防災國家重點實驗室，上海 200092)

矩形高層建筑平均風壓的風洞阻塞效應試驗研究

黃 劍，顧 明*

(同濟大學土木工程防災國家重點實驗室，上海 200092)

基于同步測壓技術，在同濟大學TJ-2建筑風洞中進行了單體矩形高層建筑的阻塞效應試驗研究。對阻塞度為4.1%、6.1%、8.4%、10.1%的剛性建筑模型在低湍流均勻風場中進行了測壓試驗，對結果進行了對比分析。主要研究了阻塞效應對模型表面平均風壓特性的影響。試驗結果表明:在均勻流中，阻塞效應對模型迎風面平均風壓系數的影響較小，除靠近角部測點外，影響幅度不足5%;阻塞效應使模型側面、背風面和頂面平均風壓系數降低較為顯著，但平均風壓系數分布規律沒有明顯變化。此外，基于風洞試驗結果提出了均勻流中矩形高層建筑平均風壓的阻塞效應修正公式。

阻塞效應;風洞試驗;高層建筑;平均風壓系數;阻塞修正

0 引 言

風洞試驗是結構風工程研究的重要手段之一。在風洞中模擬建筑的真實風環境，以確定建筑的氣動力特性和周圍的流場特性。建筑風洞通常是閉口直流式或閉口回流式，以壁面為邊界，而實際建筑在大氣流場中并無邊界。用風洞的有限空間來模擬實際大氣的無限空間必然伴隨著洞壁干擾，造成建筑氣動力和流場方面的差別。此外，結構風工程的研究對象多為鈍體，當氣流流經建筑時會產生較為寬闊的側面繞流和尾流，從而阻塞效應尤為顯著。風洞壁面對氣流繞流的約束稱為“實體阻塞”，對尾流的約束稱為“尾流阻塞”，上述兩種洞壁干擾即為阻塞效應［1］。

至今涉及建筑結構風洞試驗阻塞效應的研究較少。一些學者［2-6］在相同風洞中變化二維方柱模型縮尺比，分別提出二維方柱阻力系數的修正公式，但試驗條件和公式形式各不相同，無法為三維模型的阻塞修正提供指導。也有少數學者對三維模型阻塞效應研究。Hunt［7］對湍流邊界層流場中的立方體模型進行測壓試驗表明，8%的阻塞度對平均風壓的影響不足2%，對脈動風壓的影響不足10%。作者指出對于低矮建筑最大容許的阻塞度為10%。徐永定和呂錄勛［8-9］對切角三角形高層建筑分別進行測力和測壓試驗，研究了不同來流風向角和湍流度下的阻塞效應。謝壯寧等［10］對三種縮尺比的低矮房屋標準模型進行了測壓對比試驗，認為當阻塞度為4.9%時，阻塞效應不能忽視。Wang等［11］基于某高層建筑實際工程項目，對兩種縮尺比的剛性測壓模型進行風洞試驗，比較了建筑表面平均和脈動風壓系數。

關于建筑模型風洞試驗阻塞效應雖然有一定的研究，但至今并沒有獲得風工程研究人員的廣泛認識，也未有公認的阻塞修正方法。本文以不同縮尺比的單體矩形高層建筑模型為試驗對象，在低湍流均勻流中研究了模型表面平均風壓特性。對比了各模型迎風面、側面、背風面和頂面的平均風壓系數。采用二維方柱的修正方法對試驗結果進行修正。修正結果表明，二維方柱的修正方法并不能很好地適用于本試驗結果。在Peitzman方法的基礎上提出了適用于本試驗的平均風壓系數阻塞效應修正公式。

1 風洞試驗概況

1.1 風場模擬

試驗在同濟大學土木工程防災國家實驗室風洞試驗室TJ-2大氣邊界層風洞中完成。該風洞試驗段長15 m，寬3 m，高2.5 m，風速為0.5～60 m/s連續可調。在不同縮尺比模型試驗時采用相同的均勻風場，控制來流風速為14 m/s。圖1為風洞空載時擬安裝模型位置處的平均風速和湍流度剖面。由于風洞邊界層的影響，0.3 m以下的區域內平均風速和湍流度剖面的均勻性不如上部。

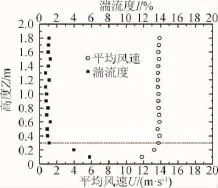
圖1 平均風速和湍流度剖面Fig.1 Mean wind speed and turbulence profile

1.2 模型概況

風洞試驗模型采用4種縮尺比，阻塞度變化范圍為4.1%～10.1%。模型尺寸見表1。各模型的測點布置圖見圖2～圖4。圖5為風洞試驗中基本坐標的定義。圖6為俯視圖及各面命名。本文僅在0°風向角(模型寬面迎風)的情況下進行數據分析。

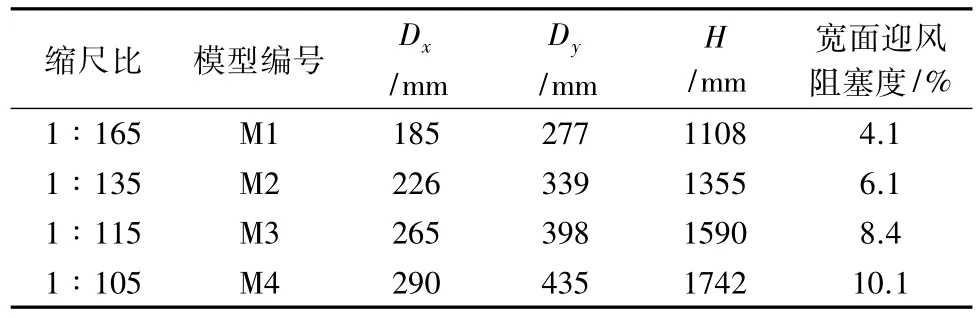
表1 模型尺寸Table 1 Size of the model

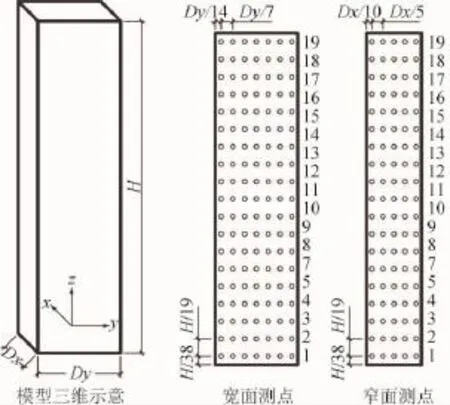
圖2 模型立面及測點布置Fig.2 Vertical view of the model and tap arrangement

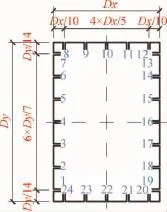
圖3 層測點布置Fig.3 Tap arrangement of layers

試驗模型采用5 mm厚有機玻璃板制作，測點直徑為1.1 mm，測壓管與掃描閥之間用PVC管連接。測壓管長度均采用1 m，以避免測壓管長度不同或管道過長所帶來的誤差。試驗數據采用相同的管道函數來修正［12］。

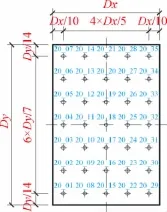
圖4 頂面測點布置Fig.4 Tap arrangement on the top

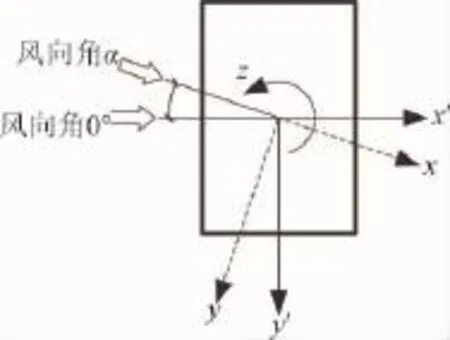
圖5 基本坐標定義Fig.5 Definition of the basic coordinate

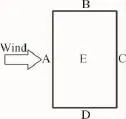
圖6 俯視圖及各面命名Fig.6 Top view and name of surface

2 試驗數據分析

2.1 平均風壓系數

各測點平均風壓系數為:

為方便分析，將各模型的平均風壓系數與模型M1的平均風壓系數差值與M1的平均風壓系數之比稱為各模型平均風壓系數的相對差值:

式中，SMi為模型Mi的平均風壓系數，i=2～4。

圖7為模型各面平均風壓系數，圖中橫坐標為測點序號，A、C面每層7個測點，B、D面每層5個測點，E面共35個測點，布置方法可參見圖2～圖4。圖7 (a)和圖7(c)中，測點1～7為第一層，測點8～14為第二層，以此類推。圖7(b)中，測點1～5為第一層，測點6～10為第二層，以此類推。對于迎風面A面測點，在較低的位置，M1的平均風壓明顯低于其它模型，主要由于邊界層的影響;在整個高度上，迎風面平均風壓系數受阻塞度的影響幅度較小。對于側面、背風面和頂面，隨著阻塞度增加平均風壓系數明顯降低，但各表面平均風壓系數的分布規律并沒有改變。

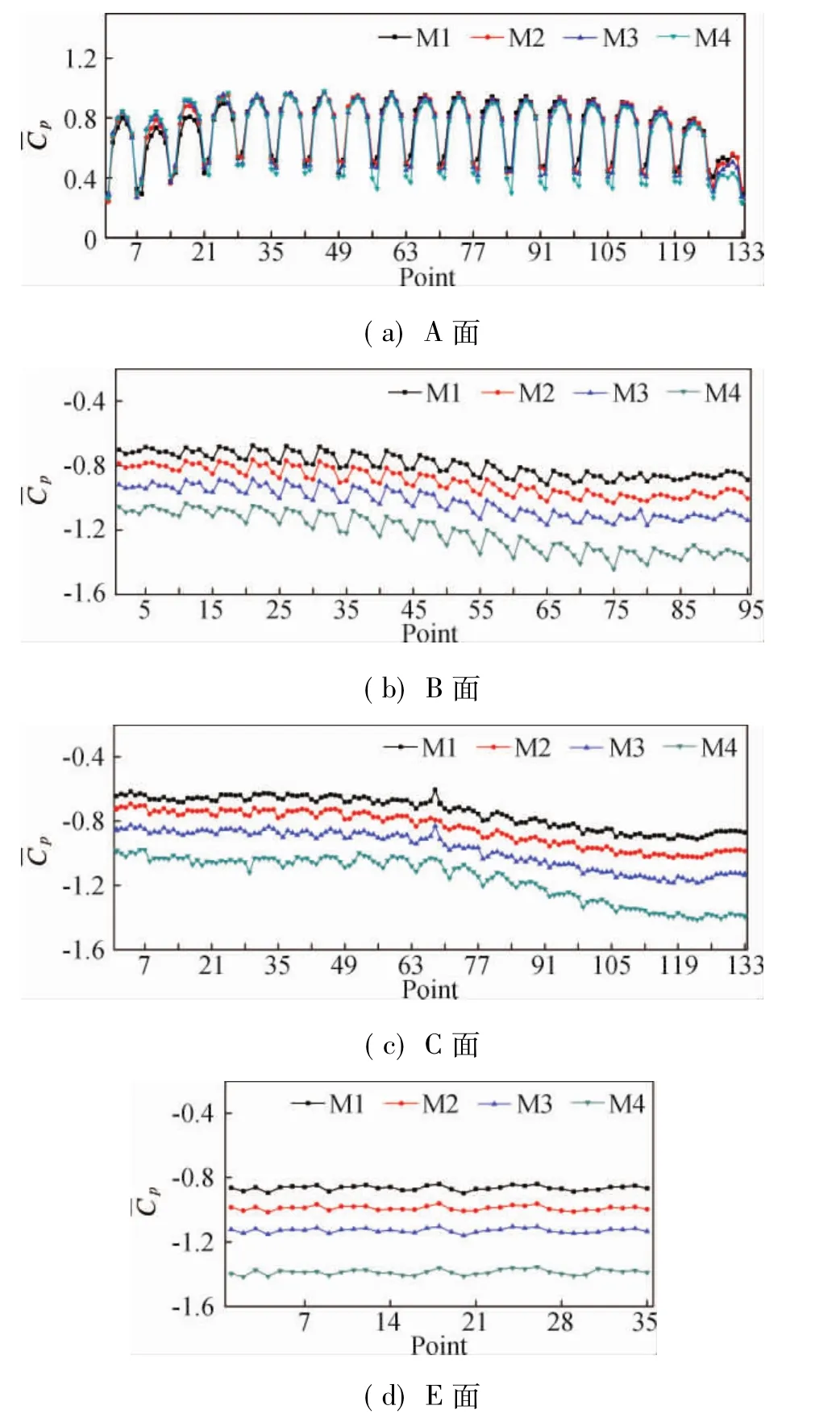
圖7 模型表面平均風壓系數Fig.7 Mean pressure coefficient on model surfaces

圖8為模型各面平均風壓系數與M1的相對差值。對于迎風面A面測點，模型M1～M4在較低位置、最高層和角部測點的相對差值較大，在其它位置的相對差值較小。在同一阻塞度時，側面、背風面和頂面平均風壓系數的相對差值都接近同一數值，阻塞度越大相對差值越大。但對于模型M4，側面和背風面的平均風壓系數的相對差值的在整個表面上的一致性不如模型M2和M3。

圖8 模型表面平均風壓系數相對差值Fig.8 Relative difference of mean pressure coefficient on model surfaces

表2列出了各模型迎風面、側面、背風面和頂面平均風壓系數相對差值的均值。由于邊界層影響，僅對10層以上的測點進行統計。在計算迎風面測點相對差值時每層靠近邊緣的兩個測點和19層測點不統計。由表可知，阻塞效應對模型迎風面平均風壓系數的影響不足5%，但側面、背風面和頂面的阻塞效應比較明顯。對比于阻塞度為4.1%的模型M1，當阻塞度為6.1%時，各面平均風壓系數的相對差值為13.4%～14.5%;當阻塞度為8.4%時，各面平均風壓系數的相對差值為29.2%～30.5%;當阻塞度為10.1%時，各面平均風壓系數的相對差值為52.9%～60.5%。可見，對于較大阻塞度的模型，負壓區測點平均風壓已產生較大的畸變。

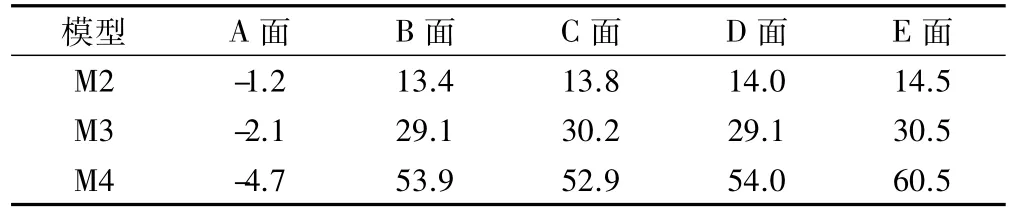
表2 模型表面平均風壓系數相對差值的均值(單位:%)Table 2 Mean relative difference of average pressure coefficient on model surfaces(unit:%)

試驗中的平均風速為14 m/s，模型的雷諾數范圍為Re=1.46×105～4.17×105，屬于同一量級。并且對于本文矩形柱這樣的帶有尖角的鈍體，分離點固定在迎風前緣的角部位置，且模型截面長寬比較小不會發生再附，所以雷諾數的影響可忽略［13］。在風場方面，試驗采用均勻流場，排除了來流給試驗結果帶來的差別。所以，阻塞效應是上述結果差別的主要原因。

2.2 試驗中皮托管的壓力

試驗中模型位置附近安裝兩個皮托管:Pitot_1安裝于模型前方2.5 m處的風洞壁面，距地面1.8 m;Pitot _2安裝于模型前方1 m處的風洞頂面，距地面2.2 m。

表3為試驗時風洞中皮托管處的平均風速和動壓的相對差。其中相對差值的計算參考式(2)。由表3可知，Pitot_1處的平均風速受阻塞度影響較小; Pitot_2處的平均風速隨著阻塞度的增加而增大。由Pitot_2處動壓的相對差可見，在所有阻塞度下，動壓的增幅均在4%以內。對比表3和表2可知，阻塞效應所引起的模型表面平均風壓系數的增大遠大于參考點動壓的增大，參考動壓的變化并不足以修正阻塞效應。

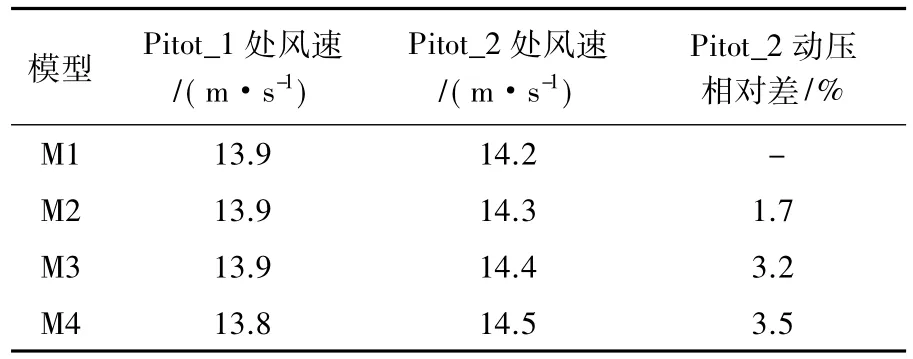
表3 皮托管平均風速及動壓的相對差Table 3 Mean velocity and relative difference of dynamic pressure on pitot tube

2.3 修正方法

2.3.1 前人的修正方法

對于類似于本文模型的鈍體結構的風洞試驗阻塞度修正方法主要有兩種:Maskell法［14］和Peitzman法［15］。

Maskell法是根據動量定理輔以經驗關系導出的修正公式:

式中，q為經過阻塞度修正后的模型處的動壓力;qu為風洞空載時流經模型處的動壓力;為阻塞比;Cxu為試驗測得的模型阻力系數。

Peitzman法是根據質量守恒定理推導，并進行簡化的修正公式:

上述兩種方法本質是一致的，均認為阻塞效應引起了模型處的風速增大。Maskell法在參考動壓修正時，除了考慮阻塞度外還將試驗測得的阻力系數作為參數。

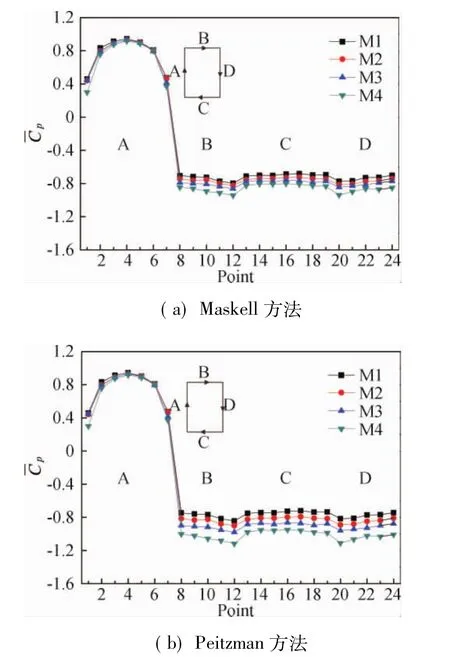
圖9 模型2/3H測點平均風壓系數修正結果Fig.9 Correction of mean pressure coefficient on 2/3H of the model

圖9為模型2/3H處測點平均風壓系數采用上述方法修正的結果，僅對側面和背風面平均風壓系數修正。由圖可見，經過Maskell法修正后，不同阻塞度下側面和背風面的風吸力的差異有所改善，但仍有一些差別;Peitzman法對阻塞效應的估計不足，各組數據間差別較大。總體看來，兩種方法對平均風壓系數的修正結果并不理想，需要發展更好的修正方法。

2.3.2 本文提出的修正方法

由于Peitzman方法形式簡單，原理易于理解，將其作進一步修正，提出適合于本文試驗的平均風壓系數的阻塞效應修正公式。根據前面的分析，在Peitzman法中引入阻塞效應調整因子k，公式如下所示:

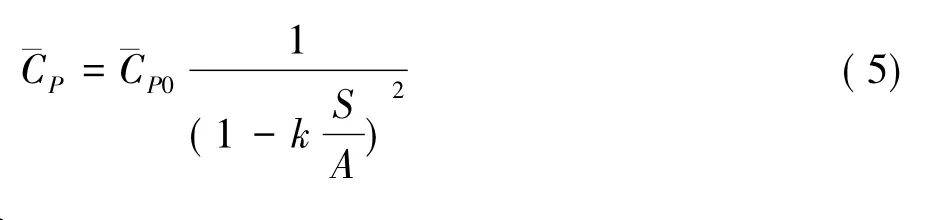
迎風面測點無需修正，通過式(5)對模型側面、背風面和頂面測點的數據最小二乘擬合，得到相應參數。基于1/2H高度以上平均風壓系數擬合參數，結果見于圖10。由圖可見，各面不同測點的擬合結果較為接近。對圖10中相同面上測點的參數擬合結果進行了平均處理，結果見于表4中。由表4可見，各面擬合的參數差別較小。為了方便實際應用，將k取為平均值2.84。新的修正公式可表示為:

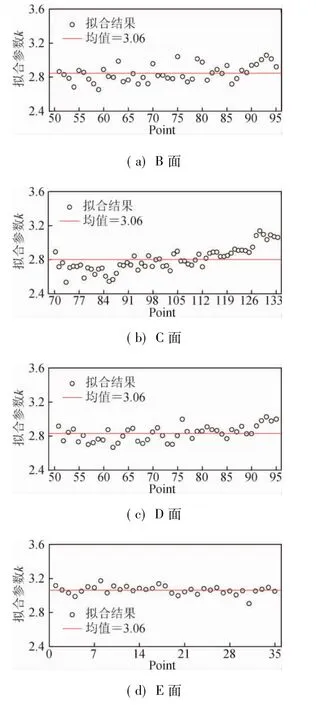
圖10 參數k的擬合結果Fig.10 Parameter fitting of k

采用式(6)分別對0°和90°風向角下2/3H處測點平均風壓系數修正，修正結果示于圖11中，可見修正結果較為滿意。

表4 各面測點擬合參數的平均值Table 4 Mean fitting parameters of measure points on all surfaces

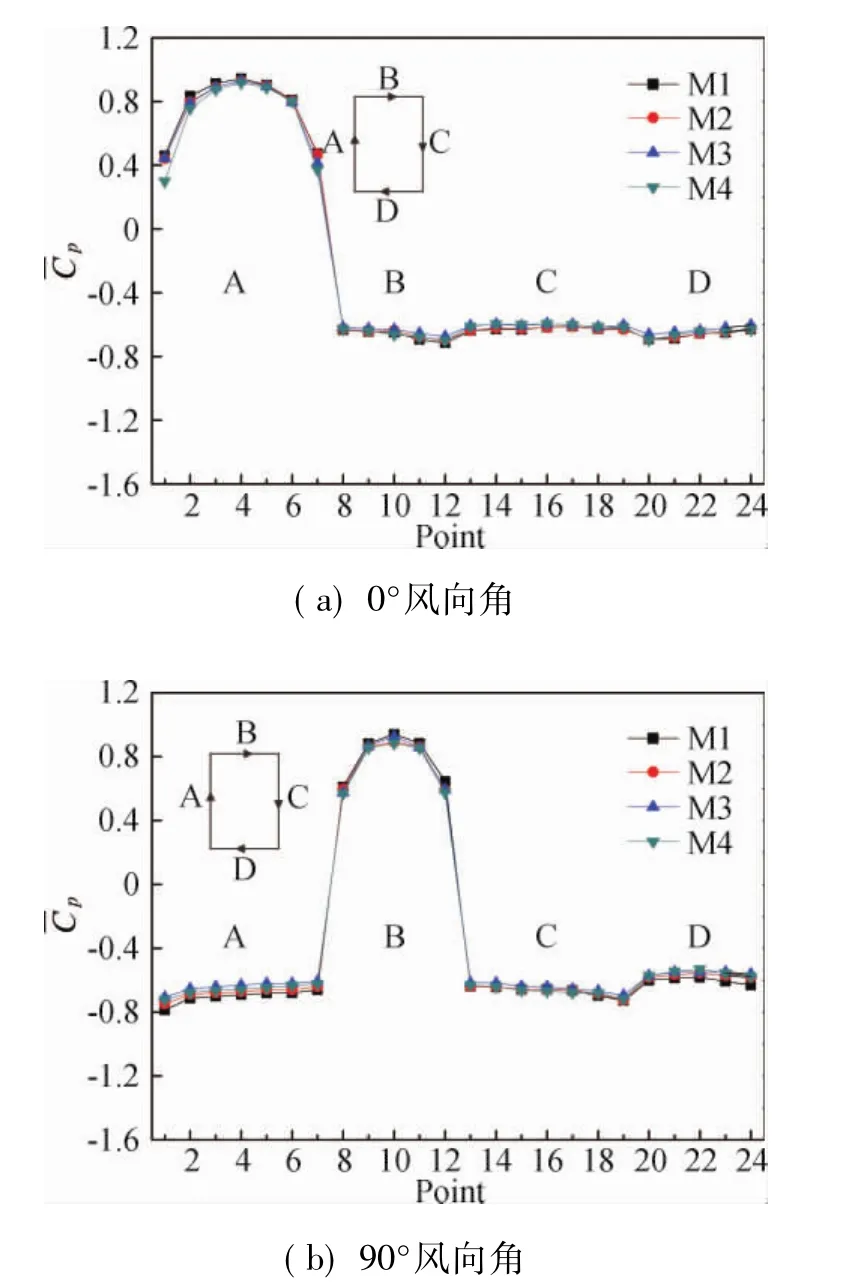
圖11 模型2/3H處平均風壓系數Peitzman改進方法修正結果Fig.11 Corrected mean pressure coefficient on 2/3H of the model by improved Peitzman method

3 結 論

本文通過剛性模型測壓試驗，研究了阻塞效應對均勻流場中單體矩形高層建筑表面平均風壓系數的影響，主要結論如下:

(1)模型迎風面平均風壓系數隨阻塞度的增大有所減小，除最接近角部位置測點影響較大外，迎風面平均風壓系數的影響不足5%，可忽略;

(2)模型側面、背風面和頂面平均風壓系數受阻塞效應的影響較大，阻塞度越大平均風壓系數明顯降低。對比于阻塞度為4.1%的模型，當阻塞度為6.1%、8.4%和10.1%時，各面平均風壓系數的增幅分別為13.4%～14.5%、29.2%～30.5%和52.9%～60.5%。但阻塞效應沒有顯著影響平均風壓系數的分布規律;

(3)依據現有試驗數據，提出了單體矩形高層建筑模型表面平均風壓的阻塞效應修正公式，修正結果較為滿意。

［1］ Cheng Houmei.Wind tunnel experiment interference and correction［M］.Beijing:National Defence Industry Press，2003.(in Chinese)

程厚梅.風洞實驗干擾與修正［M］.北京:國防工業出版社，2003.

［2］ Raju K G R，Singh V.Blockage effects on drag of sharp-edged bodies［J］.Journal of Wind Engineering and Industrial Aerodynamics，1975，1(3):301-309.

［3］ AwbiH B.Wind-tunnel-wallconstrainton two-dimensional rectangular-section prisms［J］.Journal of Wind Engineering and Industrial Aerodynamics，1978，3(4):285-306.

［4］ Laneville A，Trepanier J Y.Blockage effects in smooth and turbulent flows:the case of two-dimensional rectangular cylinders［J］.Journal of Wind Engineering and Industrial Aerodynamics，1986，22(2-3): 169-176.

［5］ Laneville A.Turbulence and blockage effects on two dimensional rectangular cylinders［J］.Journal of Wind Engineering and Industrial Aerodynamics，1990，33(1-2):11-20.

［6］ Noda M，Utsunomiya H，Nagao F.Basic study on blockage effects in turbulent boundary layer flows［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，54/55:645-656.

［7］ Hunt A.Wind tunnel measurements of surface pressures on cubic building models at several scales［J］.Journal of Wind Engineering and Industrial Aerodynamics，1982，10(2):137-163.

［8］ Xu Yongding，Lyu Luxun.Wind tunnel wall blockage effects on corner cut triangular prisms［J］.Aerodynamic Experiment and Measurement＆Control，1987，1(2):21-26.(in Chinese)

徐永定，呂錄勛.切角三角形柱體模型的洞壁阻塞干擾研究［J］.氣動實驗與測量控制，1987，1(2):21-26.

［9］ Xu Yongding，Lyu Luxun.Wind tunnel wall blockage effects on pressure distributions of hexagonal prisms［J］.Aerodynamic Experiment and Measurement＆Control，1989，3(3):21-25.(in Chinese)

徐永定，呂錄勛.多角柱體表面壓力洞壁阻塞干擾的試驗研究［J］.氣動實驗與測量控制，1989，3(3):21-25.

［10］Xie Zhuangning，Liu Shuai，Shi Biqing.Investigation into wind tunnel test of standard low-rise building model［J］.Journal of South China University of Technology(Natural Science Edition)，2011，39(6):106-112.(in Chinese)謝壯寧，劉帥，石碧青.低矮房屋標準模型的風洞試驗研究［J］.華南理工大學學報(自然科學版)，2011，39(6):106-112.

［11］Wang L，Liang S G，Tang H Q，et al.Investigation on wind tunnel blockage effect of super high-rise building［C］//The Seventh International Colloquium on Bluff Body Aerodynamics and Applications.Shanghai，China，2012.

［12］Zhou Xuanyi，Gu Ming.Optimization of dynamic pressure measurement of single-channel tubing systems［J］.Journal of Tongji University(Natural Science Edition)，2003，31(7):798-802.(in Chinese)

周晅毅，顧明.單通道測壓管路系統的優化設計［J］.同濟大學學報(自然科學版)，2003，31(7):798-802.

［13］Larose G L，D Auteuil A.On the Reynolds number sensitivity of the aerodynamics of bluff bodies with sharp edges［J］.Journal of Wind Engineering and Industrial Aerodynamics，2006，94(5):365-376.

［14］Maskell E C.A theory for the blockage effects on bluff bodies and stalled wings in a closed wind tunnel［R］.ARC R＆M 3400，1963.

［15］Peitzman F W.Low speed wind tunnel investigation to develop high attitude wall correction in the Northrop 7×10-foot low speed wind tunnel［R］.NOR 78-20，1978.

Experimental investigation of blockage effects on mean pressure of rectangular tall buildings in the wind tunnel

Huang Jian，Gu Ming*
(State Key Laboratory for Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China)

Blockage effects of an isolated rectangular tall building are investigated in the TJ-2 Boundary Layer Wind Tunnel in Tongji University using the synchronous wind pressure measurement technique.Pressure tests of rigid models with blockage ratios of 4.1%，6.1%，8.4%and 10.1%are conducted in the low turbulent uniform flow and results are compared and analyzed.Blockage effects on mean pressure characteristics on model surfaces are emphasized.The results show that in the uniform flow blockage effects on mean pressure coefficients on windward surface of the model are slight and less than 5%except for the corners.Blockage effects reduce mean pressure coefficients on side，leeward surfaces and roof obviously，while the distributions of mean pressure coefficients are almost unchanged.In addition，a new correction formula for mean pressure coefficients is proposed based on the test results.

blockage effect;wind tunnel test;tall building;mean pressure;blockage correction

TU 317+.1;TU 973+.32

A

10.7638/kqdlxxb-2013.0073

0258-1825(2015)03-0414-07

2013-07-04;

2013-11-02

國家自然科學基金(91215302，90715040)

黃劍(1986-)，男，江蘇南通人，博士研究生，主要研究高層建筑抗風.E-mail:huangjiannt@126.com

顧明*(1957-)，男，江蘇興化人，博士，教授，博士生導師，從事結構風工程研究.E-mail:minggu@tongji.edu.cn

黃劍，顧明.矩形高層建筑平均風壓的風洞阻塞效應試驗研究［J］.空氣動力學學報，2015，33(3):414-419.

10.7638/kqdlxxb-2013.0073 Huang J，Gu M.Experimental investigation of blockage effects on mean pressure of rectangular tall buildings in the wind tunnel［J］.Acta Aerodynamica Sinica，2015，33(3):414-419.