航空發動機螺栓連接薄層單元建模方法

姚星宇，王建軍，翟學

(北京航空航天大學 能源與動力工程學院，北京100191)

螺栓連接結構具有構造簡單、可操作性好等特點［1］，因此在機械結構系統中被廣泛應用，如航空發動機機匣和轉子的連接［2-3］.近年來，航空發動機不斷向高轉速、高推重比發展，使得螺栓連接結構對整機模型動力特性影響越來越大.從20 世紀80 年代開始，美國NASA 報告［4］和Sandia實驗室白皮書［5］就有關于螺栓連接結構的研究內容.可見，螺栓連接結構建模方法研究一直是結構動力學研究領域的熱點問題［6-8］.

起初，人們將螺栓連接結構接觸面設置為剛性連接，忽略所有接觸面對整體結構的影響，這樣處理使得結構剛度增加從而影響其動力學特性.隨著有限元法和接觸理論的發展，Liu 等［2-3，9］建立了三維實體有限元模型，即精細有限元模型.該模型保留了結構的幾何特征，需使用較小的單元尺寸進行網格劃分，從而導致模型自由度數目龐大，因此在航空發動機整機建模中不宜采用.為了降低問題規模，Ahmadian 等［10-11］利用彈簧、阻尼單元對螺栓連接結構進行建模，并通過試驗結果對剛度、阻尼系數進行修正，但是這些方法均將螺栓連接結構面—面接觸簡化為點—點接觸而且忽略了剪切剛度，因此運用到復雜機械模型中仍存在困難，特別是在航空發動機螺栓連接結構建模中，上述方法均存在局限性.

在復雜機械連接結構中，Ahmadian 等［12］運用薄層單元法［13-14］對AWE-MACE 機構中的連接部位進行動力學建模，將連接結構面—面接觸等效為厚度很薄的實體單元，并運用優化算法結合模態試驗結果對薄層單元材料參數進行修正;馬雙超等［15］將薄層單元法運用到航空發動機領域，對靜子機匣焊接部位進行動力學建模，并運用模態試驗結果對材料參數進行動力學修正.由此可知，薄層單元能夠模擬復雜機械中的連接結構并保持結構完整性，但薄層單元法還未應用到航空發動機螺栓連接結構建模領域中，更沒有從最基本的力學原理出發給出航空發動機螺栓連接結構薄層單元法建模原理、薄層單元材料參數理論推導以及應用前景.

因此，本文以薄層單元法為基礎，探討航空發動機螺栓連接結構薄層單元建模原理，確定薄層單元相關材料參數，并與精細有限元模型結果進行對比，從而驗證薄層單元法的正確性和應用前景.

1 薄層單元法建模原理

圖1 所示為某航空發動機典型螺栓連接，其中包括兩個部件間的連接，如進氣機匣與風扇機匣螺栓連接(圖1(a))和加力擴散器與加力筒體螺栓連接(圖1(b))，以及多個部件間的連接，如燃燒室后套壁、低壓渦輪機匣與渦輪后承力框架螺栓連接(圖1(c)).根據結構主要承載方式及連接件定位要求的不同，航空發動機螺栓連接可以分為以下3 種形式:①普通螺栓連接;②帶止口螺栓連接;③精密螺栓連接，詳細分類如表1 所示.這3 種連接形式有其共同點:①均帶有法蘭安裝邊;②螺栓連接的構件多為薄壁圓筒;③承受載荷主要為軸向載荷、彎矩、橫向載荷和扭矩.因此根據共同點可將其簡化為短粗薄壁圓筒螺栓連接結構(見圖2)作為分析模型.

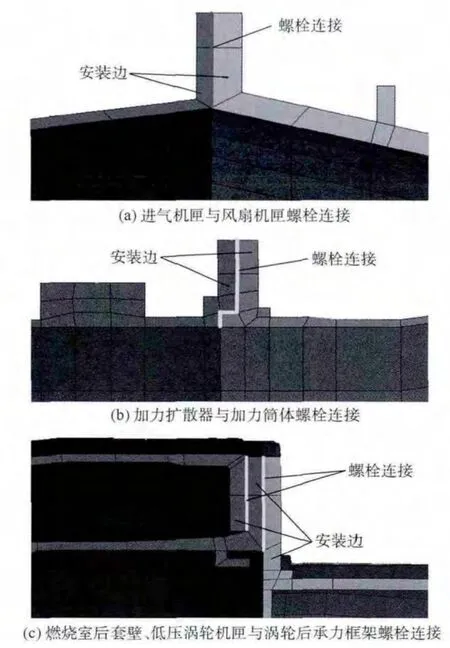
圖1 某航空發動機典型螺栓連接結構Fig.1 Typical aero-engine bolted joints structure

表1 航空發動機螺栓連接分類Table 1 Classification of aero-engine bolted joints

圖2 薄壁圓筒螺栓連接結構Fig.2 Bolt joints thin-walled cylinder structure

當螺栓預緊力足夠大或者外界激勵幅值相對小時［13，6］，可以忽略螺栓連接處的非線性性質并將其線性化.航空發動機螺栓連接在結構裝配、組裝和定位起重要作用，而且為了盡可能減小螺栓連接帶來的剛度損失，經常使用帶止口螺栓連接［2-3］和精密螺栓連接并使用較大預緊力進行預緊，因此忽略航空發動機螺栓連接結構的非線性，運用薄層單元法對航空發動機螺栓連接進行參數化建模，考慮3 個剛度作用，即軸向剛度、彎曲剛度、剪切剛度.首先介紹薄層單元法有限元計算方程的形成過程，然后給出螺栓連接結構軸向、彎曲、剪切剛度的數學表達形式，最后進行小結.

1.1 薄層單元法有限元計算方程形成

薄層單元可用通用四面體或六面體單元生成.假設薄層單元為8 節點六面體實體單元，節點坐標系為笛卡兒坐標系.8 節點六面體實體單元中任一點位移坐標(x，y，z)與節點坐標(xi，yi，zi)的關系可表示為

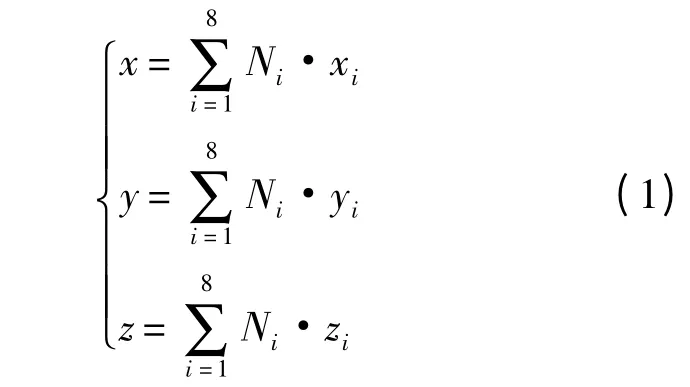
式中:Ni為形函數.

根據彈性力學基本方程，單元應變(ε)、單元應力(σ)與節點(a)的關系為

式中:B 為幾何矩陣;D 為彈性矩陣.

忽略螺栓連接結構對接面各方向耦合剛度［16-17］，則彈性矩陣為

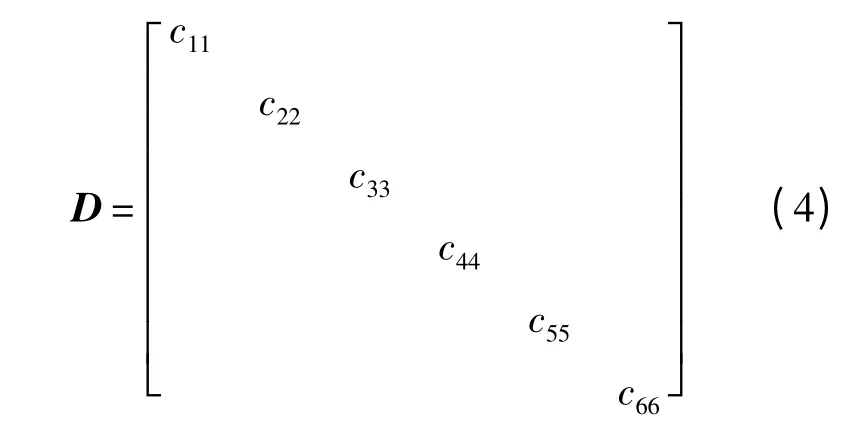
式中:c11、c22、c33為3 個方向的彈性模量;c44、c55、c66為3 個平面的剪切模量，彈性矩陣所在坐標系與節點坐標系一致.

根據虛功原理，單元剛度矩陣為

式中:V0為有限元單元的體積.

集合單元剛度矩陣Ke和節點力向量Fe形成螺栓連接結構剛度矩陣K 和節點載荷向量F，得到靜力學有限元計算方程:

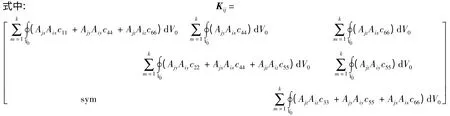
其中:i，j =1，2，…，n;?Ni/?x =Aix;?Ni/?y =Aiy;?Ni/?z=Aiz;k≤8 為某節點所在單元的個數.結構剛度矩陣K 是3n ×3n 階矩陣，包括了薄層單元和非薄層單元.

對于薄層單元厚度的選擇，Desai 等［14-15，18］都對其進行了研究.結果表明，如果不考慮界面的附加質量和阻尼，厚度的影響會很小.下面給出螺栓連接結構軸向、彎曲和剪切剛度的數學表達形式.

1.2 軸向剛度

螺栓連接結構軸向剛度定義如圖3 所示，假設薄壁圓筒一端固定，另一端在圓筒中心節點j上施加軸向載荷FN，其中x 為軸向方向，y、z 代表薄壁圓筒結構橫向方向.結構的軸向位移Δlx由節點i 的軸向位移值Xi表示，則螺栓連接結構軸向剛度定義為

代入邊界條件和載荷，求解式(6)可得

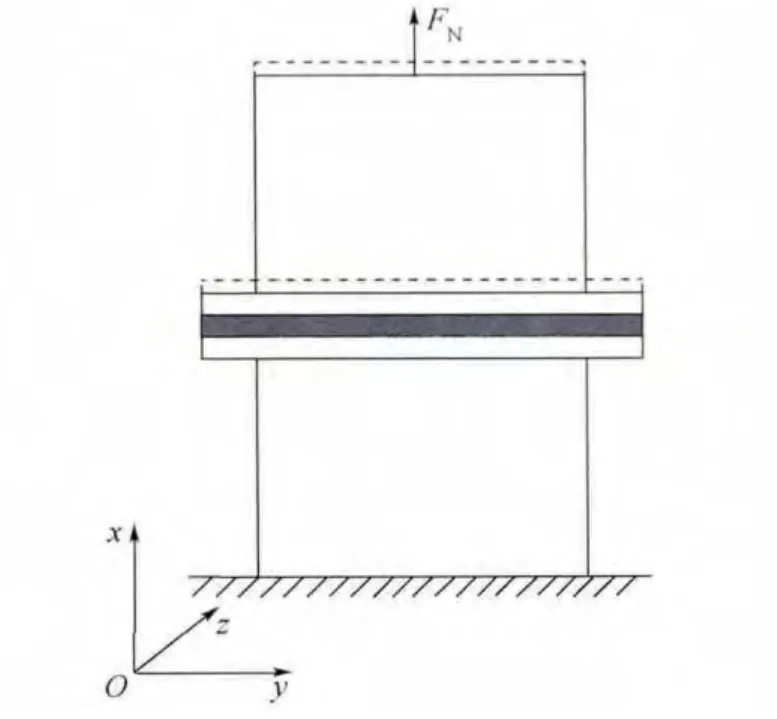
圖3 螺栓連接結構軸向剛度定義Fig.3 Definition of axial stiffness of bolted joints structure

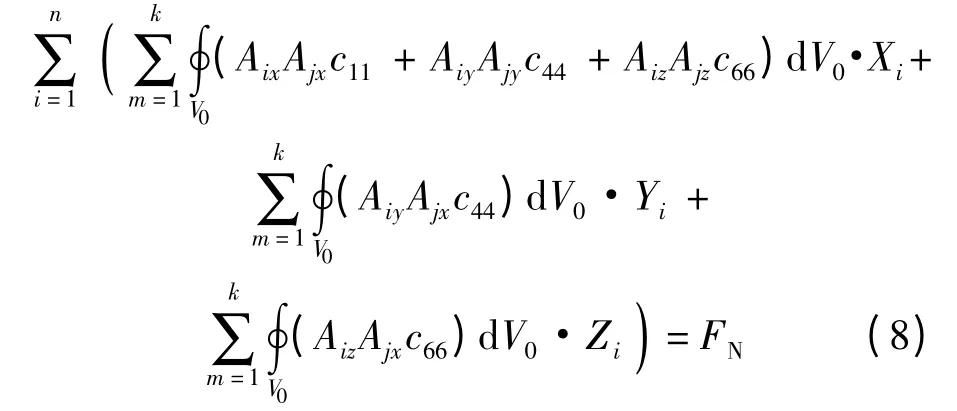
式中:Xi、Yi、Zi為節點位移.

對于薄層單元，厚度h 較單元其他兩個方向的特征尺寸小得多，所以在圖3 所示的節點坐標系xyz 下，可近似認為［19］

代入形函數Ni可得

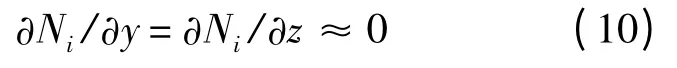
而且當螺栓連接結構受到軸向力作用時，結構的橫向位移幾乎為0，即

將式(10)和式(11)代入式(8)，軸向剛度簡化為

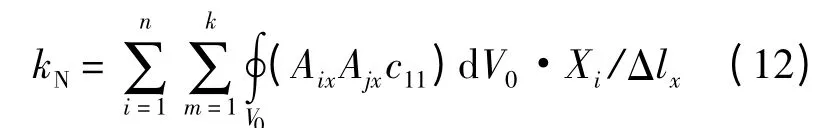
結構剛度矩陣K 包括薄層單元和非薄層單元.從式(12)可以看出，當結構的截面尺寸和單元類型確定時，軸向剛度kN由軸向彈性模量c11確定.因此，當非薄層單元材料屬性不變時，軸向剛度kN由薄層單元軸向彈性模量確定.

1.3 彎曲剛度

根據文獻［20］可知，當薄壁圓筒螺栓連接結構受到橫向載荷作用時，基于連接結構的軸向剛度，可以獲取其等效彎曲剛度，即連接結構的彎曲剛度可由軸向剛度表示:

式中:M 為彎矩;θ 為轉角;b 為圓筒的外徑.

從式(13)可以看出，螺栓連接結構彎曲剛度kM與軸向剛度kN、截面尺寸有關.因此在薄壁圓筒尺寸確定情況下，彎曲剛度kM由薄層單元軸向彈性模量確定.

1.4 剪切剛度

螺栓連接結構剪切剛度定義如圖4 所示，假設薄壁圓筒一端固定，另一端在圓筒中心節點j上施加y 向剪切載荷FSy.橫向剪切力作用產生的結構橫向位移由節點i'的y 向位移值Δly表示，則螺栓連接結構的y 向剪切剛度可定義為

圖4 螺栓連接結構剪切剛度定義Fig.4 Definition of shear stiffness of bolted joints structure

代入邊界條件和載荷，可得

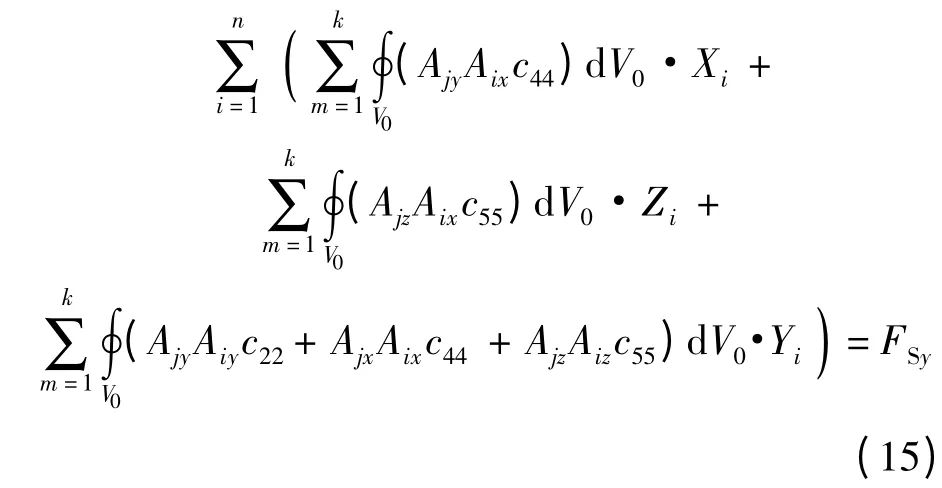
同理［21］，將式(10)代入式(15)，螺栓連接結構y 向剪切剛度簡化為

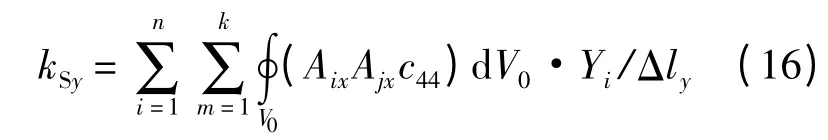
同理，螺栓連接結構z 向剪切剛度為

式(16)和式(17)表明螺栓連接的剪切剛度與剪切模量有關，因此當非薄層單元的材料屬性和結構截面尺寸不變時，剪切剛度kS由薄層單元剪切模量決定，其中xy 平面剪切模量決定y 向剪切剛度，xz 平面剪切模量決定z 向剪切剛度.

綜上所述，航空發動機螺栓連接結構的軸向剛度、彎曲剛度可由薄層單元軸向彈性模量確定，剪切剛度可由薄層單元橫向剪切模量來確定.

2 薄層單元對連接剛度影響規律

第1 節詳細敘述了航空發動機螺栓連接結構薄層單元法建模原理，現闡述薄層單元材料參數對連接剛度的影響規律.

2.1 建 模

圖5 所示為薄層單元薄壁圓筒螺栓連接結構有限元模型，單元類型為SOLID185.由于航空發動機螺栓連接結構軸向、彎曲剛度由薄層單元軸向彈性模量確定，剪切剛度由薄層單元橫向剪切模量確定，為了使薄層單元材料參數互不影響且忽略各個方向耦合剛度［13，17］，將其設置為正交各向異性材料，材料屬性設置如表2 所示.

圖5 薄壁圓筒螺栓連接有限元模型Fig.5 Finite element model of thin-walled cylinder bolted joints

表2 有限元模型材料屬性Table 2 Material properties of finite element model

在該模型中，x 軸代表圓筒的軸向，y、z 軸分別代表圓筒的橫向，那么薄層單元的Ex、Ey、Ez分別表征連接處軸向(x 向)、橫向(y 向、z 向)的剛度，Gxy、Gyz、Gxz分別表征xy 平面、yz 平面、xz平面的剪切剛度.因此在該模型中，對軸向、彎曲剛度起決定作用的是軸向(x 向)彈性模量Ex，對剪切剛度起決定作用的是xy、xz 平面的剪切模量Gxy、Gxz.由于航空發動機螺栓連接結構大多數是帶止口的螺栓連接或精密螺栓連接，剪切剛度可認為是無限大，因此本節中不對剪切剛度進行驗證，只驗證軸向剛度和彎曲剛度的建模原理.

2.2 軸向剛度影響規律

對圖5 所示的有限元模型一端完全約束，另一端施加載荷為2 kN 的軸向力，改變薄層單元材料參數，得到對軸向剛度的影響規律.

2.2.1 剪切模量對軸向剛度的影響

保證彈性模量E 不變，改變剪切模量G(3 個平面值一致).圖6 所示為軸向剛度隨剪切模量G改變的變化曲線圖.研究表明:①當薄層單元彈性模量E 分別為100、10、1 GPa 時，隨著剪切模量G的變化，軸向剛度幾乎不變，說明剪切模量對軸向剛度幾乎沒有影響;②當彈性模量E 較小時(1 GPa)，隨著剪切模量的改變，軸向位移有一定改變，但變化程度在3%以內.根據式(8)可以看出，當彈性模量E 較小時，Ai1Aj1c11、Ai2Aj2c44、Ai3Aj3c66的共同影響造成了這種結果，但這種影響可以忽略.

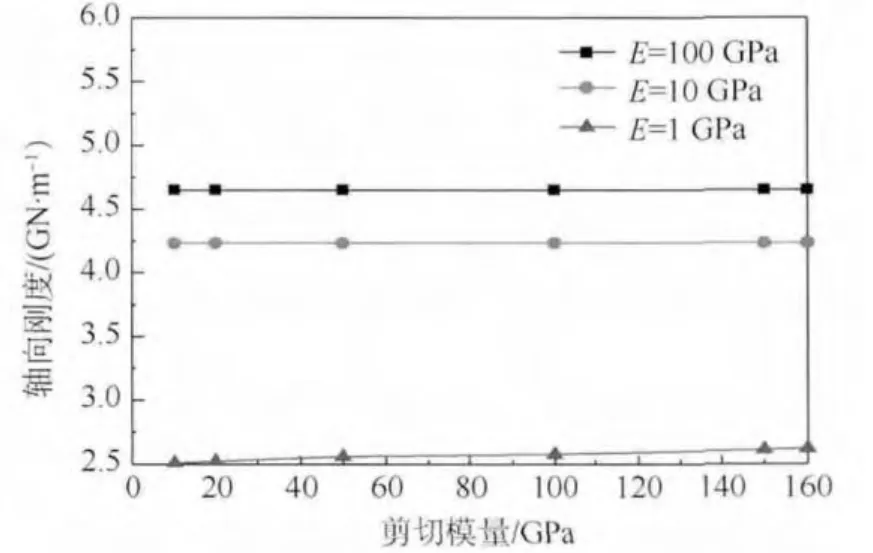
圖6 剪切模量對軸向剛度的影響Fig.6 Influence of shear modulus on axial stiffness

2.2.2 彈性模量對軸向剛度的影響

保證剪切模量G 不變(均取180 GPa)，然后依次改變Ex、Ey、Ez(值不變時取10 GPa).圖7 所示為軸向剛度隨彈性模量Ex、Ey或Ez改變的變化曲線圖.研究表明:①當剪切模量一定時，改變彈性模量Ey、Ez值，軸向剛度幾乎不變，說明Ey、Ez對機匣軸向剛度沒有影響;②當剪切模量一定時，改變彈性模量Ex，軸向剛度有明顯變化，說明軸向彈性模量對軸向剛度有很大影響，特別是當Ex較小時影響更大.

現分析軸向彈性模量對軸向剛度具體影響規律.從圖7 可以看出:①隨著軸向彈性模量的減小(160 ～18 GPa)，軸向剛度線性逐漸減小，但剛度變化趨勢并不明顯;②當彈性模量減小到一定時(18 GPa 附近)，軸向剛度突然減小，并存在一個明顯的拐點;③當通過拐點之后，機匣軸向剛度又線性減小，但剛度變化趨勢比160 ～18 GPa 間大很多.

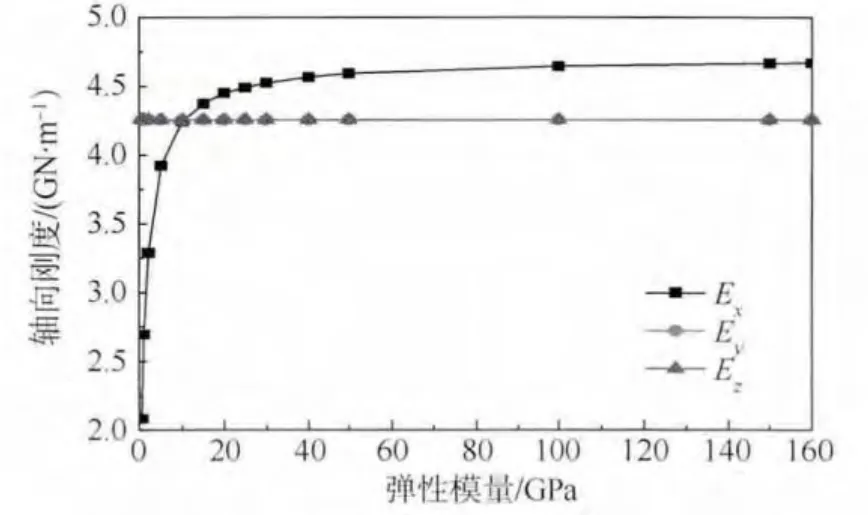
圖7 不同方向彈性模量對軸向剛度的影響Fig.7 Influence of elastic modulus on axial stiffness

圖8 Ex =160 GPa 和1.8 GPa 時機匣軸向位移圖Fig.8 Axial displacement when Ex is 160 GPa and 1.8 GPa

從上述分析可知，軸向彈性模量對機匣軸向剛度影響是存在兩段線性變化的區間，這主要是隨著軸向彈性模量的改變，整個機匣承受軸向力的部位發生了變化，造成軸向位移分布發生了變化.如圖8 所示，當軸向彈性模量較大時，薄層單元處的軸向剛度比較大，并且與圓筒部分軸向剛度值相差不大，因此整個圓筒結構共同承受軸向力，機匣軸向位移云圖是均勻分布的，如圖8(a)所示.隨著軸向彈性模量逐漸減小，此時薄層單元處軸向剛度也逐漸減小，并且與圓筒部分軸向剛度相差越來越大，因此逐漸從整個圓筒結構共同承受軸向力變為連接處薄層單元單獨承受，此時軸向變形主要發生在薄層單元，機匣圓筒部分主要發生軸向剛性位移，如圖8(b)所示.這也解釋了軸向彈性模量的改變引起整個結構軸向剛度非線性變化的原因.

2.3 彎曲剛度影響規律

對圖5 所示的機匣有限元模型一端完全約束，另一端施加載荷為2 kN·m 的彎矩，改變薄層單元的材料屬性參數，得到對彎曲剛度的影響規律.

2.3.1 剪切模量對彎曲剛度的影響

保證彈性模量不變，改變剪切模量G，圖9 所示為彎曲剛度隨著剪切模量G 改變的變化曲線圖.研究表明:①當薄層單元彈性模量E 分別為100、10、1 GPa 時，隨著剪切模量G 的變化，彎曲剛度幾乎不變，說明剪切模量對彎曲剛度沒有影響;②當彈性模量E 較小時(1 GPa)，隨著剪切模量的改變，彎曲剛度有一定改變，但變化程度在3%以內.這主要是因為當彈性模量E 較小時，Ai1Aj1c11、Ai2Aj2c44、Ai3Aj3c66共同影響造成的結果，但這種影響可以忽略.

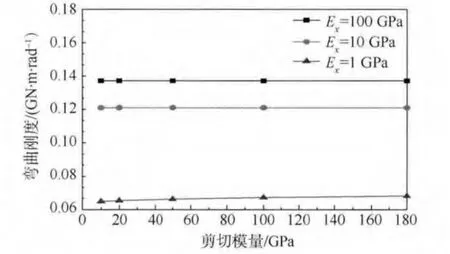
圖9 剪切模量對彎曲剛度的影響Fig.9 Influence of shear modulus on bending stiffness

2.3.2 彈性模量對彎曲剛度的影響

保證剪切模量G 不變(取180 GPa)，依次改變Ex、Ey、Ez(值不變時取10 GPa).圖10 所示為彎曲剛度隨著彈性模量改變的變化曲線圖.研究表明:①當剪切模量一定時，改變彈性模量Ey、Ez值，彎曲剛度幾乎不變，說明Ey、Ez對機匣彎曲剛度沒有影響;②當剪切模量一定時，改變軸向彈性模量，彎曲剛度有明顯變化，說明軸向彈性模量對機匣彎曲剛度有很大影響.

現分析軸向彈性模量對彎曲剛度的影響規律.從圖10 中可以看出:①隨著軸向彈性模量的減小(160 ～18 GPa)，彎曲剛度線性逐漸減小，但剛度變化的趨勢并不大;②當軸向彈性模量減小到一定程度(18 GPa 附近)，彎曲剛度突然減小，并存在明顯的拐點;③當通過拐點后，彎曲剛度又線性減小，但剛度變化趨勢比160 ～18 GPa間大.

圖10 不同方向彈性模量對彎曲剛度的影響Fig.10 Influence of elastic modulus on bending stiffness

圖11 Ex =130 GPa 和1.8 GPa 時機匣Von Mises 位移圖Fig.11 Von Mises displacement of casing when Ex is 130 GPa and 1.8 GPa

從上述分析可知，軸向彈性模量對彎曲剛度影響主要是存在兩段線性變化的區間，這主要是隨著軸向彈性模量的改變，整個圓筒承受彎矩的部位發生了變化，從而造成位移分布改變.如圖11(a)所示，當軸向彈性模量較大時，薄層單元處的軸向剛度較大，與圓筒部分的軸向剛度值相差不大，因此在受到彎矩作用時，整個機匣共同承受彎矩，螺栓連接結構和機匣作為整體發生彎曲變形，機匣Von Mises 位移云圖是均勻分布的.當軸向彈性模量逐漸減小，此時薄層單元軸向剛度逐漸減小，并且與圓筒部分軸向剛度相差越來越大，因此在受到彎矩作用時，彎矩逐漸從整個圓筒共同承受變為連接處薄層單元單獨承受，此時變形主要發生在薄層單元，為軸向變形，存在受拉側和受壓側，且受拉側和受壓側軸向位移一致，機匣圓筒部分主要發生剛性轉角位移，如圖11(b)所示.這也解釋了軸向彈性模量的改變引起整個結構彎曲剛度非線性變化的原因.

3 薄層單元法材料參數確定

第1 節和第2 節詳細闡述了航空發動機螺栓連接薄層單元法建模原理以及薄層單元材料參數對薄壁圓筒連接剛度的影響規律，本節給出薄層單元相關材料參數的理論表達式并研究螺栓連接結構參數對連接剛度的影響規律.

由于航空發動機螺栓連接結構大多數是帶止口的螺栓連接或精密螺栓連接，剪切剛度可認為是無限大，因此本節中不考慮結構的剪切剛度，只給出軸向彈性模量的理論表達式.

3.1 螺栓連接軸向剛度理論表達式

對于一般薄壁圓筒螺栓連接結構，去掉圓筒部分，保留安裝邊及螺栓，那么連接區域可以分為3 個部分:①螺桿連接區域;②螺栓預緊力夾緊區域;③安裝邊對接面連接區域，如圖12所示，其中螺栓連接結構的軸向連接剛度主要由①、②決定.

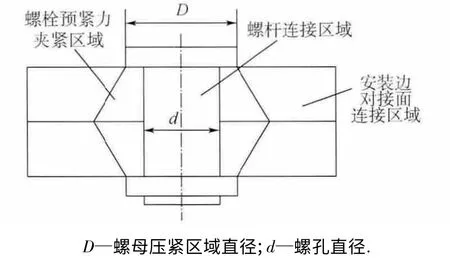
圖12 螺栓連接結構連接區域Fig.12 Connection region of bolted joints structure

對于螺桿連接區域，螺桿軸向剛度［21］可以表示為

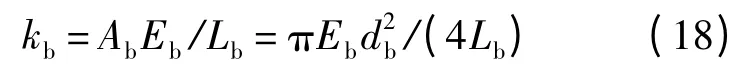
式中:Ab為螺桿截面面積;db為螺桿直徑;Lb為螺桿等效長度，可表示為Lb=L +(1.95 －β/2 －υ)db［22］，其中L、β 和υ 分別為螺孔長度、無量綱系數及螺桿泊松比，這充分考慮了螺母、墊片等對連接剛度的影響;Eb為螺桿彈性模量.在本文中Lb取L.

對于螺栓預緊力夾緊區域，該區域可近似為對稱的切去頂端的圓錐形區域，可得每塊安裝邊軸向連接剛度［23］為

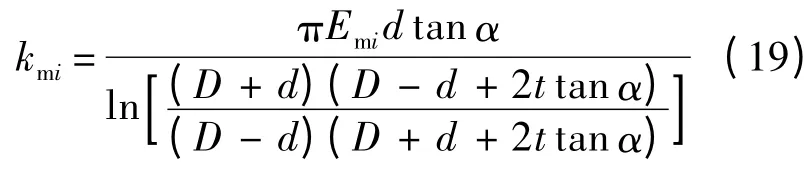
式中:Emi(i=1，2)為安裝邊彈性模量;t 為安裝邊厚度;α 為半錐形角，與螺栓預緊力Fp大小有關.

對于安裝邊厚度不同的螺栓連接結構，如圖13所示，螺栓預緊力壓緊區域為上下對稱的去頂端圓錐區域加中間的圓環區域，圓環柱狀區域的軸向連接剛度可表示為

式中:Ac為圓環面積;t'為圓環柱狀區域厚度.

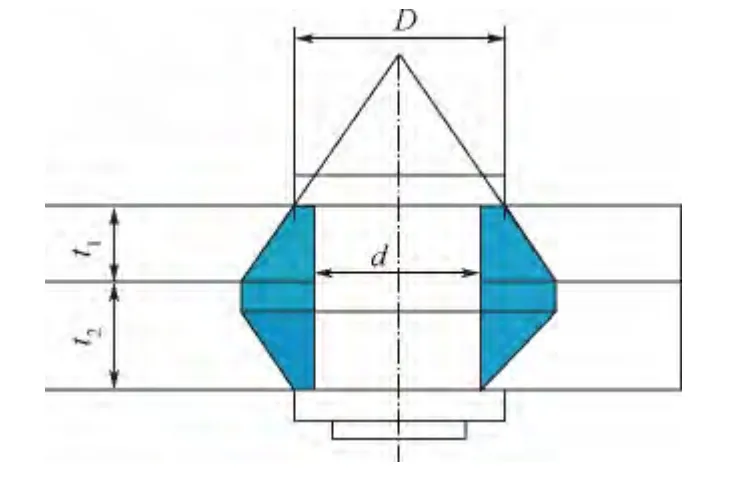
圖13 安裝邊厚度不同的螺栓連接結構Fig.13 Bolted joints structure of different thickness flange

因此整個螺栓預緊力夾緊區域軸向連接剛度為

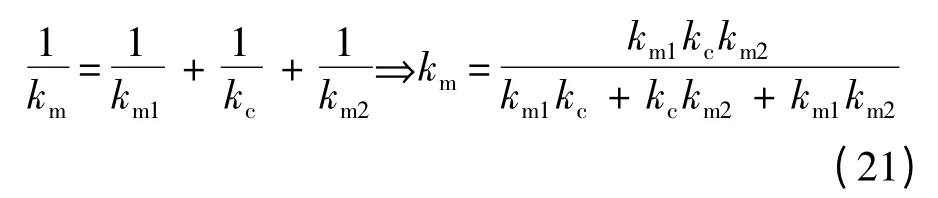
那么圖12 所示整個螺栓連接軸向剛度可表示為(式(7)為整個薄壁圓筒的軸向剛度)

式中:n 為整個法蘭邊周向螺栓的個數.

可見，整個螺栓連接軸向、彎曲剛度與螺桿彈性模量Eb、螺桿直徑db、螺孔長度L 以及安裝邊彈性模量Emi、螺栓預緊力Fp、螺母壓緊區域半徑D、螺栓數目n 有關.

3.2 結構參數對軸向剛度的影響

下面探討螺栓連接結構參數對軸向剛度的影響規律，主要研究螺栓數目n 和螺栓預緊力Fp對其的影響.

假設兩安裝邊的厚度一致，安裝邊以及螺栓的材料屬性一樣，其他結構參數如圖14 所示，那么螺栓連接軸向剛度可表示為

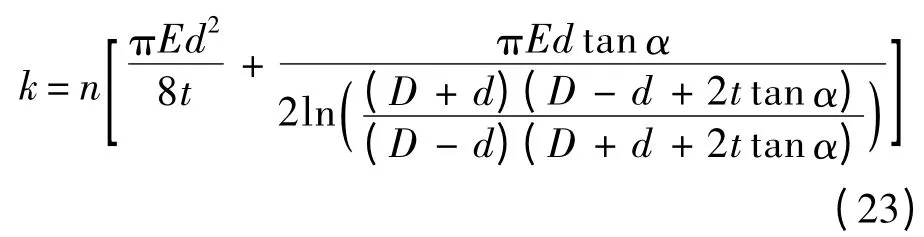
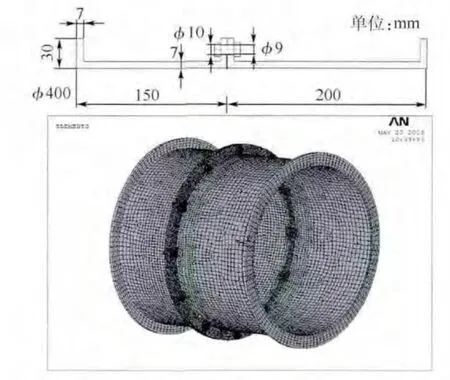
圖14 精細有限元模型Fig.14 Detailed finite element model

3.2.1 螺栓數目對軸向剛度的影響

當螺栓連接其他結構參數都確定，螺栓預緊力為3 kN 時，螺栓個數與連接剛度的變化曲線如圖15 所示.從圖中可以看出，軸向剛度隨著螺栓數目的變化線性增加，說明螺栓個數越多，螺栓連接軸向剛度越大.

圖15 螺栓個數對連接剛度影響Fig.15 Influence of bolt numbers on joint stiffness

3.2.2 螺栓預緊力對軸向剛度的影響

由于半錐形角α 與螺栓預緊力有關，因此通過半錐形角α 作為中介研究螺栓預緊力對連接剛度的影響規律.當螺栓連接其他結構參數都確定，螺栓個數為12 時，螺栓預緊力與連接剛度的變化曲線如圖16 所示.從圖中可以看出，當螺栓預緊力較小時，軸向剛度隨著螺栓預緊力的增加幾乎線性增加;當預緊力增加到一定程度時，軸向剛度趨近不變，說明此時螺栓連接已接近于剛性連接.

圖16 螺栓預緊力對連接剛度影響Fig.16 Influence of bolt preload on joint stiffness

3.3 薄層單元材料參數理論表達式

如圖17 所示，當用薄層單元法對航空發動機螺栓連接結構進行參數化建模時，結構軸向剛度可表示為(去掉圓筒，保留安裝邊和螺栓)

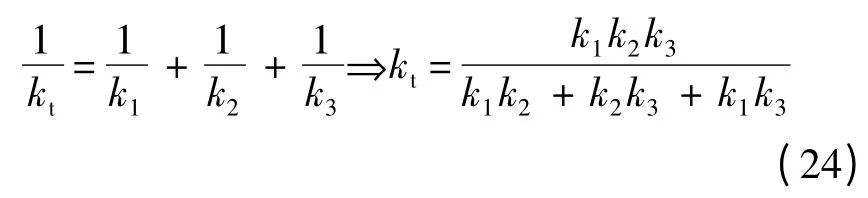
式中:k1、k2、k3分別為上安裝邊、薄層單元以及下安裝邊的剛度，表示為ki=EiAi/Li，其中Ei、Ai和Li分別表示各部分的軸向彈性模量、橫截面積以及厚度.

圖17 螺栓連接薄層單元Fig.17 Thin-layer element of bolted joints

因此，薄層單元軸向彈性模量與連接剛度的關系為

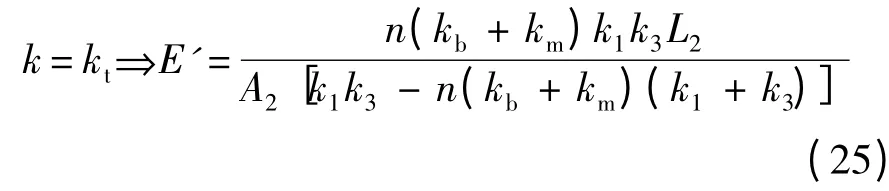
4 應 用

第1 ～3 節對薄層單元法的建模原理、材料參數對連接剛度的影響規律以及材料參數的確定進行了詳細的闡述.現在將薄層單元法應用到實際的結構中，并與精細有限元模型的結果進行對比，從而驗證薄層單元法的正確性和應用前景.

首先，通過精細有限元模型計算薄壁圓筒螺栓連接結構的軸向剛度和彎曲剛度以作為標準剛度;然后，通過第3 節內容得到薄層單元的材料參數，并計算出薄層單元薄壁圓筒的軸向、彎曲剛度;最后，將兩個模型的結果進行對比.

4.1 精細有限元模型方法

圖14 所示為薄壁圓筒精細有限元模型，法蘭邊周向有12 個M9 的螺栓，建模過程中充分考慮螺栓預緊力(PRETS179 單元模擬，設置為3 kN)、螺母與法蘭邊、螺栓頭與法蘭邊以及法蘭邊對接面間的接觸(TARGE170 和CONTA174 單元模擬)，單元類型為SOLID185，整個結構有88 333 個單元數和95 917 個節點數，結構的彈性模量為210 GPa，密度為7 850 kg·m－3，泊松比為0.3.

將該結構一端固定，另一端分別施加軸向載荷和彎曲載荷，從而得到軸向剛度和彎曲剛度(第1 節的定義)的變化曲線，如圖18 所示.

從圖18 中可以看出:①結構軸向位移隨著軸向載荷的增加線性變化，結構轉角隨著彎曲載荷的增加線性變化，說明結構的軸向剛度、彎曲剛度隨著外載荷的增加不改變;②通過計算，軸向剛度為3.35 GN/m，彎曲剛度為9.16 ×107N·m/rad.

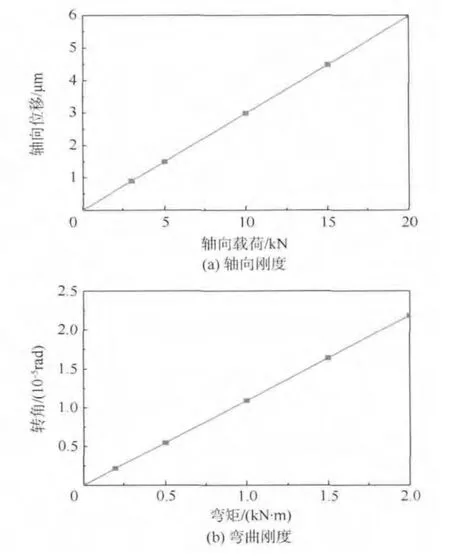
圖18 剛度變化規律Fig.18 Change law of stiffness

4.2 薄層單元法

運用薄層單元法對該結構建模，薄層單元厚度為h(h=3 mm)，單元類型SOLID185，整個結構共有19 927 單元數和28 161 節點數，薄層單元材料屬性為正交各向異性材料，橫向彈性模量為100 GPa，剪切模量為300 GPa，泊松比為0.尺寸如圖17 所示，螺桿直徑d =9 mm，安裝邊厚度t =7 mm，螺母壓緊區域直徑D =14 mm，薄層單元厚度h=3 mm，螺栓個數n =12，螺栓預緊力3 kN對應的半錐形角位α=16°，通過第3 節相關內容計算得到薄層單元軸向彈性模量E=2.62 GPa.將該結構一端固定，另一端分別施加軸向載荷和彎曲載荷，從而得到薄層單元模型的彎曲剛度為9.71×107N·m/rad，軸向剛度為3.58 GN/m.

4.3 對 比

將薄層單元薄壁圓筒螺栓連接結構的軸向剛度和彎曲剛度與精細有限元模型的結果進行對比，詳細的對比結果如表3 所示，可以得出以下結論:

1)通過薄層單元法建立的薄壁圓筒螺栓連接結構的軸向剛度、彎曲剛度與精細有限元模型(標準值)相比，彎曲剛度與軸向剛度分別只相差6%和6.8%.

2)精細有限元模型的軸向、彎曲剛度影響因素為螺桿直徑、螺栓數目、螺栓孔位置、法蘭邊厚度、預緊力，而薄層單元法模型的影響因素則只有軸向彈性模量.

3)薄層單元模型的單元數和節點數分別比精細有限元模型少78%和71%.

4)薄層單元模型的計算時間相對精細有限元模型少98%.

綜上所述，薄層單元法能夠很好地模擬航空發動機螺栓連接結構且能保證正確性，具有很好的應用前景.

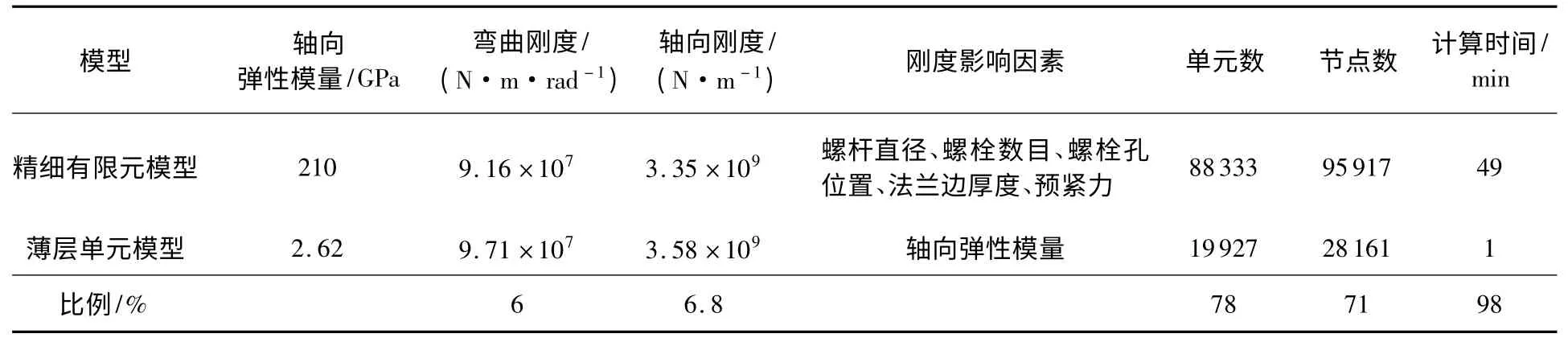
表3 薄層單元模型與精細有限元模型對比Table 3 Comparisons between detailed FE model and thin-layer element model

5 結 論

本文將薄層單元法應用到航空發動機領域，從航空發動機螺栓連接結構出發，以薄層單元法為基礎，給出了航空發動機螺栓連接結構薄層單元法參數化建模原理，研究了薄層單元材料參數對螺栓連接剛度的影響規律，并從理論上給出了薄層單元相關材料參數的表達式，最后將該方法應用到實際結構中，并與精細有限元模型結果進行對比，驗證了薄層單元法的正確性和應用前景.研究結果表明:

1)薄層單元法能很好地模擬航空發動機螺栓連接結構.

2)薄層單元剪切模量對軸向、彎曲剛度幾乎沒有影響;橫向彈性模量對軸向、彎曲剛度幾乎沒有影響.

3)薄層單元軸向彈性模量對軸向、彎曲剛度起決定作用;薄層單元剪切模量對剪切剛度起決定作用.

4)螺栓連接的螺栓數目與軸向連接剛度呈線性變化規律.

5)當螺栓預緊力較小時，軸向剛度隨著螺栓預緊力的增加線性增加;當預緊力增加到一定程度時，軸向剛度趨近不變，說明此時螺栓連接已接近于剛性連接.

6)通過精細有限元模型與薄層單元模型結果的對比，薄層單元模型剛度值與精細有限元模型相差在7%以內，而且計算時間、模型規模較精細有限元模型均大幅減少.

References)

［1］ Bickford J H.An introduction to the design and behavior of bolted joints［M］.2nd ed.New York:Marcel Dekker，Inc.，1990:1-8.

［2］ Liu S G，Wang J，Hong J，et al.Dynamics design of the aeroengine rotor joint structures based on experimental and numerical study［C］∥Proceedings of ASME Turbo Expo.New York:ASME，2010:GT2010-22199.

［3］ 樊寧.航空發動機連接結構剛度非線性及其對轉子動力學影響［D］.北京:北京航空航天大學，2013.

Fan N.Studies on dynamic characteristics of the joint in the aeroengine rotor system［D］.Beijing:Beijing University of Aeronautics and Astronautics，2013(in Chinese).

［4］ Belvin W K.Modeling of joints for the dynamic analysis of truss structures，NASA-L-16163［R］.Washington，D.C.:NASA，1987.

［5］ Gregory D L，Martinez D R.On the development of methodologies for constructing predictive models of structures with joints and interfaces，SAND2001-0003P［R］.Albuquerque:Sandia National Laboratories，2001.

［6］ Ibrahim R A，Pettit C L.Uncertainties and dynamic problems of bolted joints and other fasteners［J］.Journal of Sound and Vibration，2005，279(3-5):857-936.

［7］ Groper M.Microslip macroslip in bolted joints［J］.Experimental Mechanics，1985，25(2):171-174.

［8］ Gaul L，Nitsche R.The role of friction in mechanical joints［J］.Applied Mechanics Reviews，2001，54(2):93-106.

［9］ Kim J，Yoon J C，Kang B S.Finite element analysis and modeling of structure with bolted joints［J］.Applied Mathematical Modelling，2007，31(5):895-911.

［10］ Ahmadian H，Jalali H.Identification of bolted lap joints parameters in assembled structures［J］.Mechanical Systems and Signal Processing，2007，21(2):1041-1050.

［11］ Boeswald M，Link M，Meyer S.Experimental and analytical investigations of non-linear cylindrical casing joints using base excitation testing［C］∥2003 IMAC-XXI:Conference ＆ Exposition on Structural Dynamics.Kissimmee:Society for Experimental Mechanics，2003:1-9.

［12］ Ahmadian H，Mottershead J E，James S，et al.Modelling and updating of large surface-to-surface joints in the AWE-MACE structure［J］.Mechanical Systems and Signal Processing，2006，20(4):868-880.

［13］ Desai C S，Zaman M M，Lightner J G，et al.Thin-layer element for interfaces and joints［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1984，8(1):19-43.

［14］ Sharma K G，Desai C S.Analysis and implementation of thinlayer element for interfaces and joints［J］.Journal of Engineering Mechanics，1992，118(12):2442-2462.

［15］ 馬雙超，臧朝平，蘭海波.某航空發動機機匣的動力學模型修正［J］.航空動力學報，2013，28(4):878-884.

Ma S C，Zang C P，Lan H B.Dynamic model updating of an aero-engine casing［J］.Journal of Aerospace Power，2013，28(4):878-884(in Chinese).

［16］ Ahmadian H，Ebrahimi M，Mottershead J E，et al.Identification of bolted-joint interface models［C］∥Proceedings of the 2002 International Conference on Noise and Vibration Engineering.Leuven:Katholieke Universiteit Leuven，2002:1741-1747.

［17］ Iranzad M，Ahmadian H.Identification of nonlinear bolted lap joint models［J］.Computers and Structures，2012，96-97:1-8.

［18］ Pande G N，Sharma K G.On joint interface elements and associated problems of numerical ill-conditioning［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1979，3(3):293-300.

［19］ 黃耀英，吳中如，王德信.薄層單元基本假設和簡化探討［J］.力學與實踐，2008，30(2):49-52.

Huang Y Y，Wu Z R，Wang D X.Discuss on fundamental assumption and simplification of thin-layer element［J］.Mechanics in Engineering，2008，30(2):49-52(in Chinese).

［20］ 欒宇.航天器結構中螺栓法蘭連接的動力學建模方法研究［D］.大連:大連理工大學，2012.

Luan Y.Study on dynamic modeling of bolted flange connections in aerospace structures［D］.Dalian:Dalian University of Technology，2012(in Chinese).

［21］ Williams J G，Anley R E，Nash D H，et al.Analysis of externally loaded bolted joints:Analytical，computational and experimental study［J］.International Journal of Pressure Vessels and Piping，2009，86(7):420-427.

［22］ Pedersen N L，Pedersen P.Stiffness analysis and improvement of bolt-plate contact assemblies［J］.Mechanics Based Design of Structures and Machines，2008，36(1):47-66.

［23］ Oskouei R H，Keikhosravy M，Soutis C.Estimating clamping pressure distribution and stiffness in aircraft bolted joints by finite-element analysis［J］.Proceedings of the Institution of Mechanical Engineers，Part G:Journal of Aerospace Engineering，2009，223(7):863-871.