利用符號計算方法研究生物系統全時滯穩定性

柳君，牛薇

(北京航空航天大學 中法工程師學院，北京100191)

時滯微分系統的穩定性研究在理論和應用上都有其重要的意義，特別地，從控制理論的角度看，生物系統全時滯穩定即表明該系統對于時滯具有很好的魯棒性和可靠性.

長期以來，人們一直致力于尋找時滯微分系統全時滯穩定的代數判據，已取得了不少進展.秦元勛在文獻［1］中第1 次將單滯后多維系統的全時滯穩定判據由超越形式的檢驗轉化為代數形式的檢驗，并對n =1，2(n 為非線性時滯微分系統的維數)的情形具體給出了判定法則，雖然此方法對高維情形處理起來并不容易.在文獻［2］中，秦元勛和俞元洪根據Newton 遞推公式，對單時滯n=2 的情況進行了深入的研究.文獻［3］討論了一類線性定常時滯系統全時滯漸進穩定的充分代數判據.文獻［4-5］研究了單時滯線性系統漸進穩定的代數判據;在文獻［5］的基礎上，文獻［6］討論了多時滯線性系統漸進穩定性的代數判據.文獻［1-6］中的方法均針對線性系統，并均使用傳統的數學推導方法.模擬生物問題的動力系統通常是非線性的，較為復雜，利用傳統的數學方法很難分析其穩定性，需要借助更先進的計算方法和工具.隨著計算機科學與技術的發展，以精確計算為特點的符號計算逐漸成熟和完善，效率也逐步提高，成為數值計算的一種強有力的替代.

針對含參數的非線性生物系統，本文給出時滯微分系統全時滯穩定性的代數判據，研究如何利用符號計算方法分析多維生物系統正平衡點的漸進穩定性.文獻［7-8］提出了利用代數方法分析生物系統穩定性和分岔等問題的算法化方法，并且給出了軟件實現及實驗結果.不同于傳統的數學推導，符號計算使得求解生物系統的穩定性和分岔更加程序化和自動化.本文在作者工作的基礎上，進一步研究如何利用符號計算方法，如文獻［9］中的三角分解、文獻［10-11］中的Gr?bner 基和文獻［12］中的實解分類等方法，程序化地分析生物系統全時滯穩定性.

1 時滯微分系統正平衡點的穩定性

考慮如下n 維非線性多時滯微分系統:

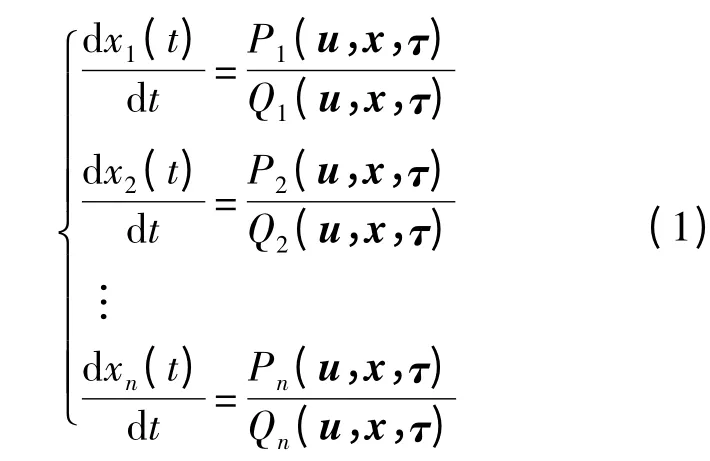
式中:P1，P2，…，Pn，Q1≠0，Q2≠0，…，Qn≠0 為多項式;u = (u1，u2，…，um)為參數;x = (x1(t)，x2(t)，…，xn(t))∈Rn為變元;τ=(τ，2τ，…，kτ)為系統的時滯，τ∈R+=［0，∞)為時滯;n、m、k為正整數.

為了計算式(1)的正平衡點，令τ=0，可得

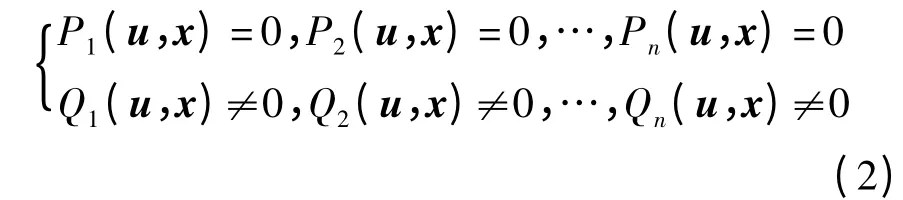
得出的解即為平衡點x*.在求出系統(1)的正平衡點之后，需要討論其平衡點x*處的穩定性.由于該系統是非線性形式，首先需進行線性化.據文獻［13］，線性化之后的系統零解的漸進穩定性與非線性系統正平衡點的漸進穩定性一致.

令y =x －x*，代入式(1)中，x*是系統的正平衡點，滿足式(2)，可得線性化之后的系統:

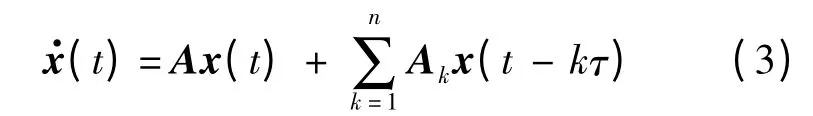
式中:A，Ak∈Rn×n為矩陣.

式(3)的特征方程為

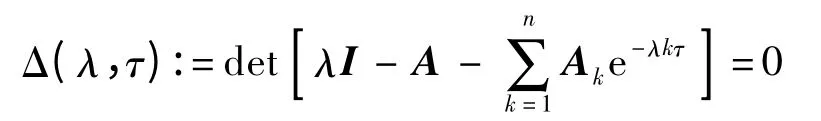
式中:I 為n×n 階單位矩陣;λ 為特征值.若特征方程的根對?τ∈R+均具有負實部，那么其零解漸進穩定，稱式(3)系統全時滯穩定.因此，式(1)系統正平衡點的漸進穩定性等價于式(3)系統零解的全時滯穩性.

2 時滯系統全時滯穩定的代數判據

時滯微分式(3)系統的全時滯穩定性，即多項式Δ(λ，τ)對?τ∈R+均Hurwitz 穩定.據文獻［14］，有

引理1 式(3)系統全時滯穩定的充分必要條件為

2)對?τ ＞0 及任意實數y，都有

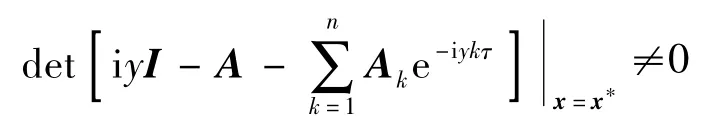
成立.其中，x*為式(2)求出的平衡點;i 為虛數單位.

對于條件1):令多項式M 為

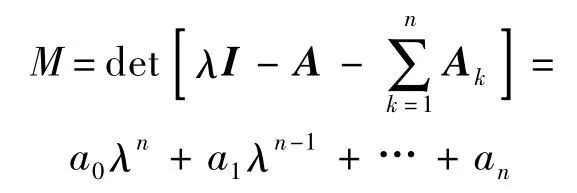
在此基礎上，定義M 的Hurwitz 矩陣:

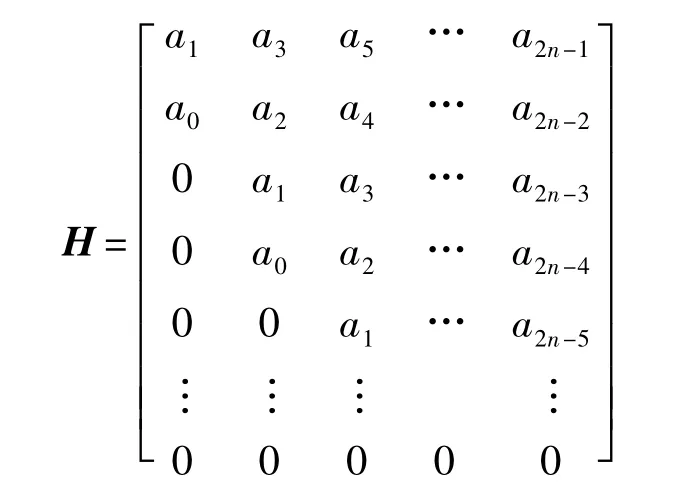
其中:當i ＞n 時，ai=0.H 的順序主子式Δ1，Δ2，…，Δn為M 的Hurwitz 行列式.根據文獻［15］Routh-Hurwitz 判據，多項式M 是穩定的，當且僅當下列條件成立:

Δ1＞0，Δ2＞0，…，Δn－1＞0，an＞0

對于條件2):對?τ ＞0 及任意y，有

成立.據文獻［14］，令－yτ =θ，則其他等價于:對?θ∈［0，2π］＞0 及任意實數y∈R－{0}，有

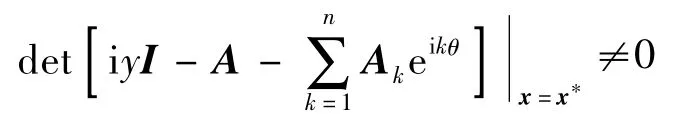
成立.作分式線性變換

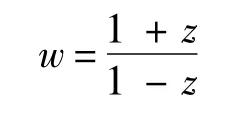
條件2)等價于:對?z∈R 及任意實數y∈R－{0}，都有

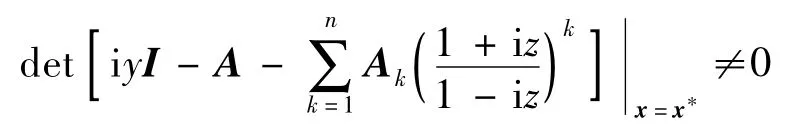
成立.在此，記

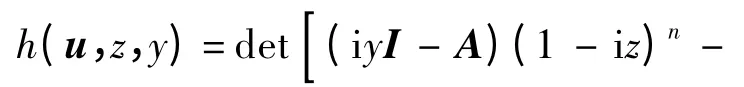
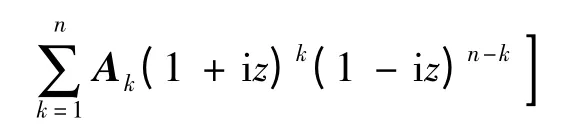
由h(u，z，y)=0 分離實部和虛部可得

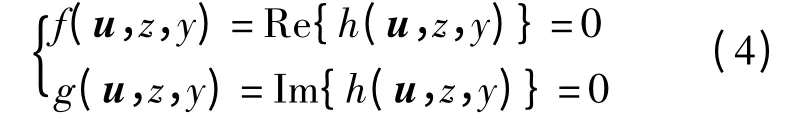
式中:f 和g 為關于z、y 的實系數含參數二元多項式，z∈R，y∈R－{0};Re 和Im 為實部和虛部.條件2)等價于式(4)無實根.由此，可得非線性多時滯微分系統全時滯穩定的充要條件.

引理2 式(1)系統正平衡點全時滯穩定的充分必要條件是式(5)系統有正實根且式(6)系統無實根:

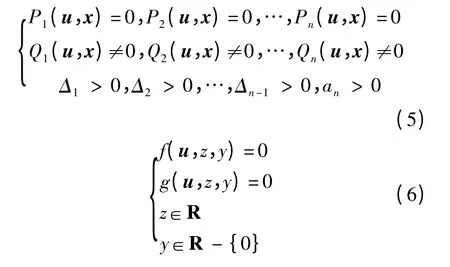
3 代數方法分析

第2 節描述了如何將時滯系統的全時滯穩定性問題化為代數問題，這里將研究如何將代數方法應用到求解這些代數問題上.

步驟1 構造半代數系統.

假設實際問題由式(1)系統來模擬，通過計算可得到含多項式方程及不等式的式(5)系統和式(6)系統.變元x 及參數u 可能需滿足一些實際問題中的附加約束:

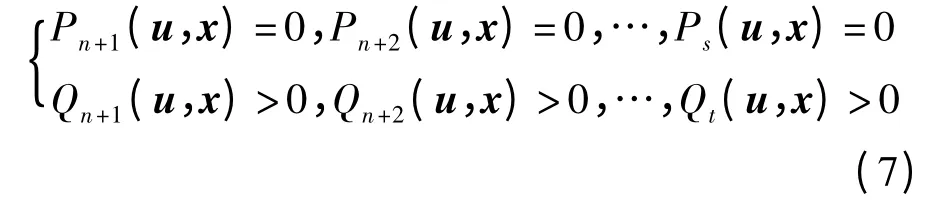
式中:s，t≥n.把約束條件式(7)加到式(5)系統和式(6)系統中，可得兩個含等式及不等式的系統，稱之為半代數系統.一般地，設半代數系統Ψ形如:

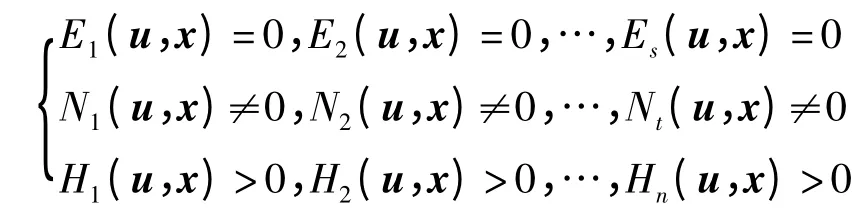
步驟2 計算三角列.

通過三角列或Gr?bner 基方法，可以把多項式集E={E1，E2，…，Es}三角化，得到三角列Tk.若參數u 出現，轉至步驟4.

步驟3 參數不出現.

如果參數u 不出現，可以用長度可無限小的有理區間來隔離每個Tk的實零點.令F = {N1，N2，…，Nt，H1，H2，…，Hn}為不等式多項式集.然后F 中的多項式在每個實零點上的符號可以通過計算它們在有理區間的端點的值來確定.由此得到用有理區間隔離的半代數系統Ψ 的實解.

步驟4 實解分類.

假設參數u 出現，令F 對于每個三角列Tk，可利用F 來計算一個關于u 的代數簇V，使得其將實參數空間Rm分為有限多個胞腔，滿足在每個胞腔上，Tk的實零點個數以及F 在這些零點處的符號不變.從每個胞腔中取一個有理樣本點，代入Tk消去參數，由步驟3 可計算Tk的實零點以及F 在該樣本點的符號.

步驟5 參數條件最后，根據多項式在Ψ 具有指定個數的實解的胞腔中樣本點處的符號，建立參數u 所需要滿足的條件.

在文獻［16］實解分類軟件DISCOVERER 的基礎上，算法步驟(見圖1)已在MAPLE 中實現.

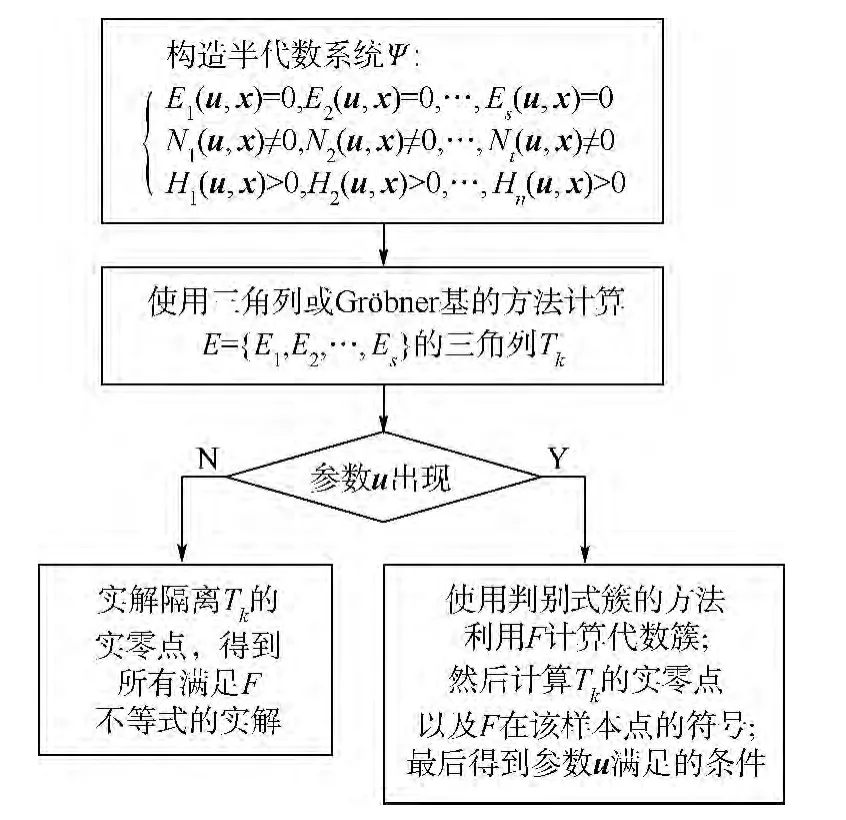
圖1 代數方法分析算法步驟Fig.1 Algorithmic steps using algebraic approaches

4 應用實例

4.1 實例驗證

文獻［13］中介紹了一種重要的生物模型:Lotka-Volterra 捕食-食餌系統.為了驗證本文中代數方法的可行性，使用這個簡單的捕食-食餌系統演示利用符號計算方法分析全時滯穩定性的流程.在此，考慮以下單時滯的捕食-食餌系統:

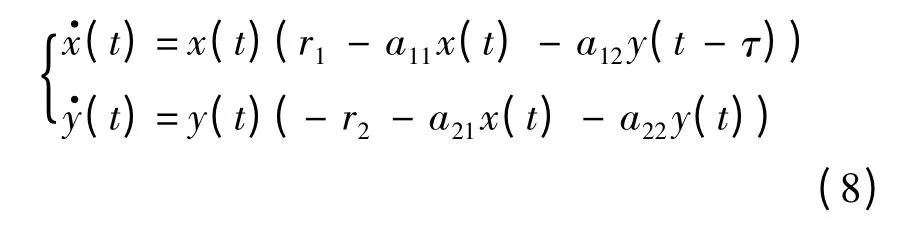
式中:x(t)＞0、y(t)＞0 為食餌、捕食者的種群密度;r1＞0、r2＞0 為食餌及捕食者的內稟增長率;aii(i=1，2)＞0 為兩種群密度作用的種群內作用系數;aij(i≠j)＞0 為兩種群相互作用的種群間作用系數;τ≥0 為捕食者的追捕時間.接下來計算該系統在平衡點處穩定的充要條件.

第1 步 分析正平衡點及線性化.

令τ=0，那么平衡點問題可化為

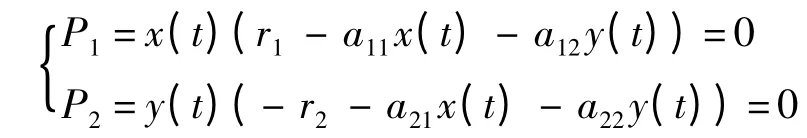
記由此求得的正平衡點x*=(x*，y*).

考慮2 ×2 階Jacobian 矩陣

式(8)系統可寫為矩陣形式:

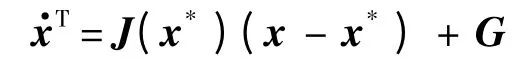
這里G 是非線性項，線性部分為

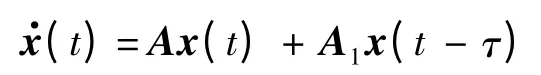
式中:

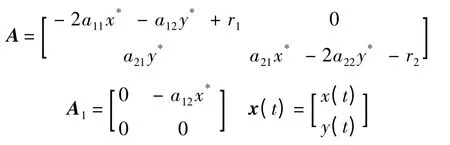
第2 步 分析條件1).

第2 節引理1 中的條件1)是det［λI －A －A1］=0 均具有負實根，在此，

M=det［λI － A － A1］=a0λ2+ a1λ + a2

式中:

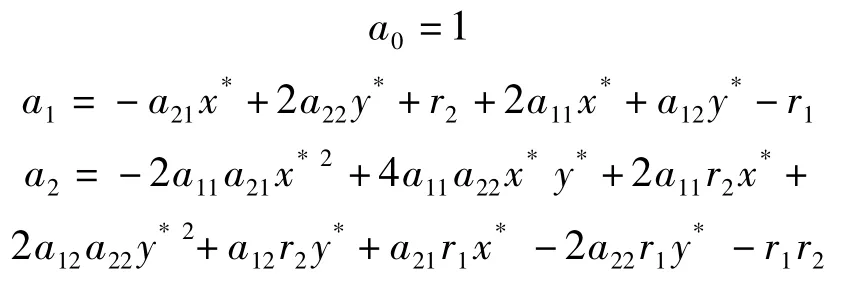
由多項式系數a0、a1、a2組成的Hurwitz 判據

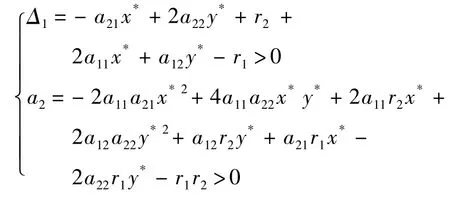
故而，可得半代數系統

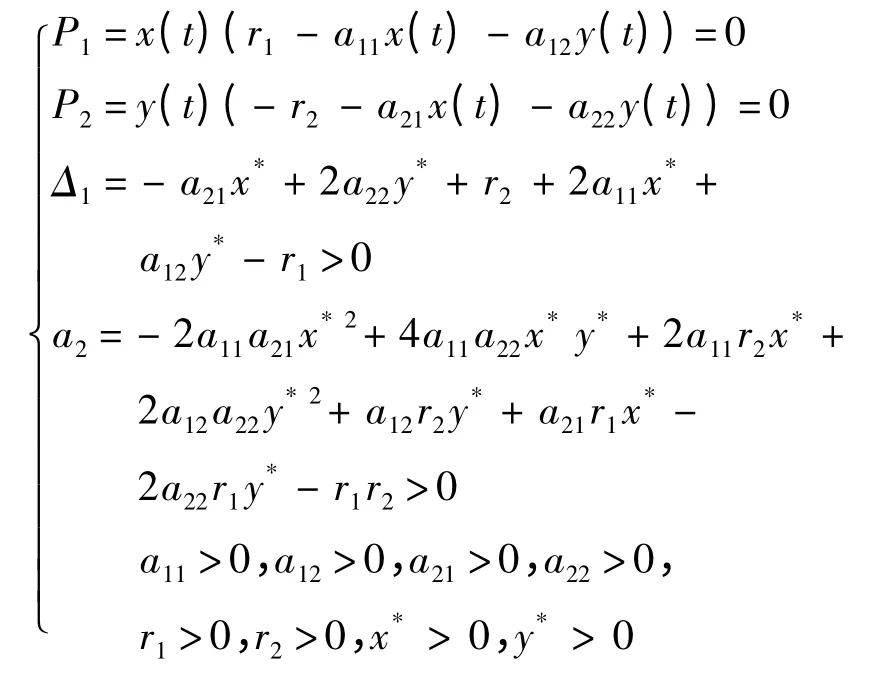
利用MAPLE 中實現的第3 節中的算法求解該半代數系統可得

R1=r1a21－ r2a11＞0

第3 步 分析條件2).

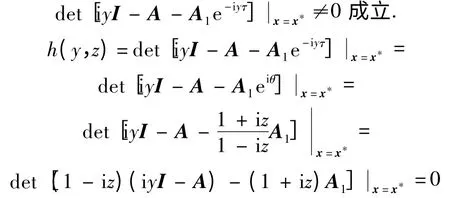
無實根.

分離h(y，z)的實部和虛部可得半代數系統

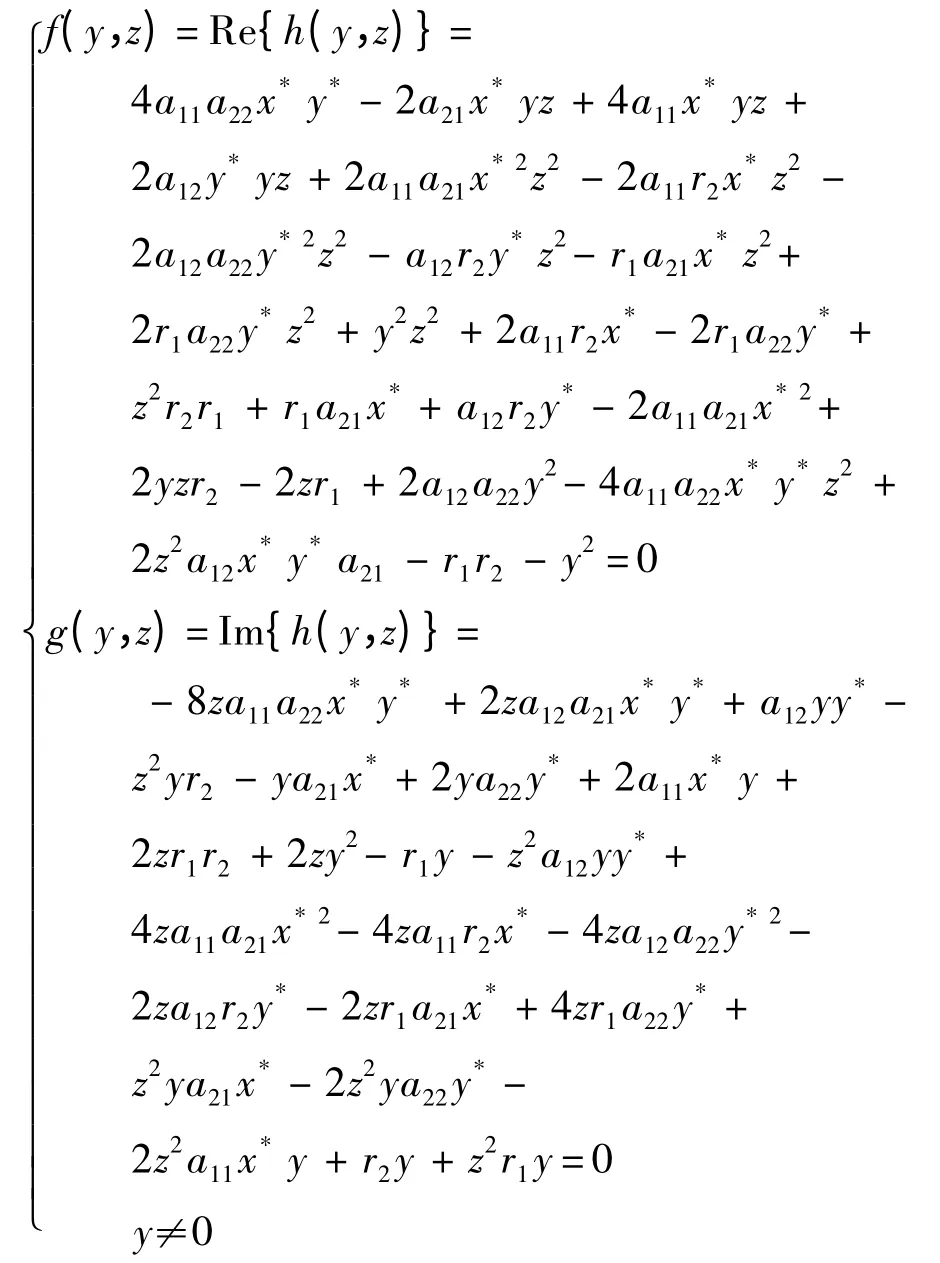
無實根.

求解該半代數系統可得

R2=a21a12－ a11a22≤0

滿足時，系統無實根.

綜上可得，當參數滿足

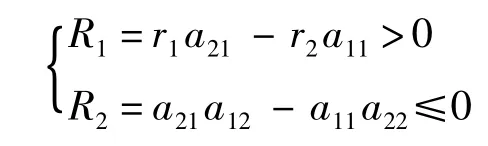
時式(8)系統在平衡點處全時滯穩定.

4.2 無選擇性的捕食-食餌系統

文獻［17］中的無選擇收獲的Lotka-Volterra捕食-食餌系統也是一種重要的數學生物模型.考慮以下二維系統:

式中:r(1 －x/k)(r，k ＞0)為無捕食者時食餌的增長率;βx/(1 + ax)(β，a ＞0)為捕食者的響應函數;d ＞0為捕食者的死亡率;α ＞0 為轉換系數;qx和Ey(q，E ＞0)分別為食餌和捕食者的收獲率.與第4.1 節的方法類似可以解決式(9)系統的全時滯穩定的問題.

第1 步 利用線性化方法和Hurwitz 判據可得半代數系統，即條件1):

求解該半代數系統可得

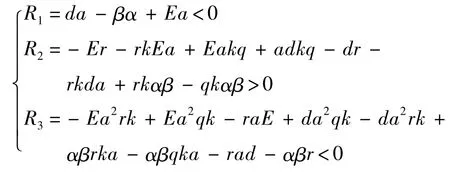
第2 步 分析條件2).

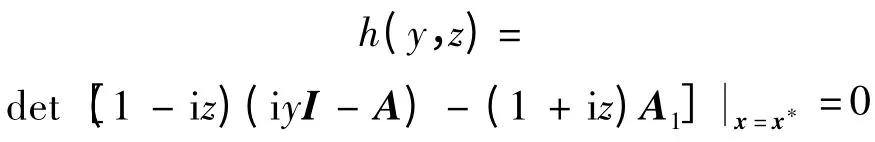
無實根.

分離h(y，z)的實部和虛部可得半代數系統

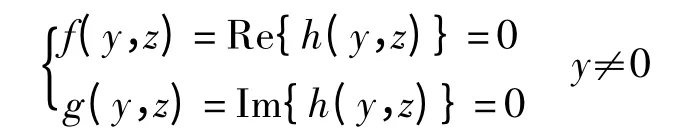
無實根.

f(y，z)和g(y，z)都是含有參數和變量的多項式.表1 中是f(y，z)和g(y，z)的項數和最高次數，該問題使用傳統的數學計算方法很難得出結果，而利用符號計算方法在幾秒之內，可得

R4= － ark + aqk － r≥0

滿足時，系統無實根.

表1 f(y，z)和g(y，z)的項數和最高次數Table 1 Number of terms and higher degree of f(y，z)and g(y，z)

所以，當參數滿足

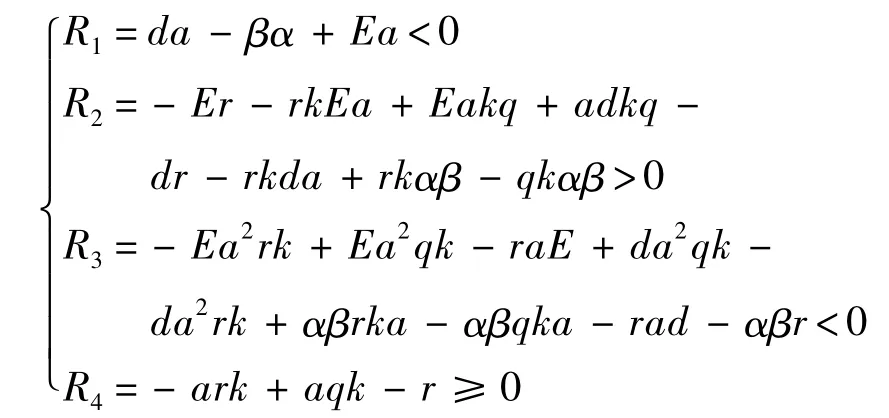
時，式(9)系統在平衡點處全時滯穩定.

4.3 SIR 傳染病模型

SIR 傳染病模型是一個重要的生物模型，Cooke 在文獻［18］中提出了時滯SIR 傳染病模型，并指出t 時刻的傳染能力為βS(t)I(t －τ')，其中，β ＞0 為每天每個感染者接觸的人數，τ'≥0為病毒在被感染者體內的作用時間.文獻［19］中時滯SIR 傳染病系統為

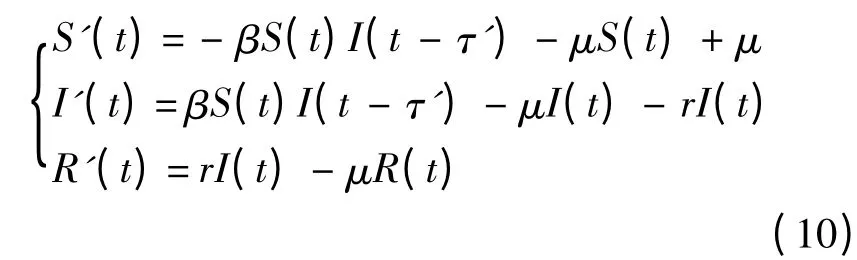
式中:μ ＞0 為死亡率;r ＞0 為日恢復速率.

第1 步 構造及分析條件1).

計算可得

R1=β － μ － r ＞0

第2 步 分析條件2).

分離h(y，z)的實部和虛部可得半代數系統

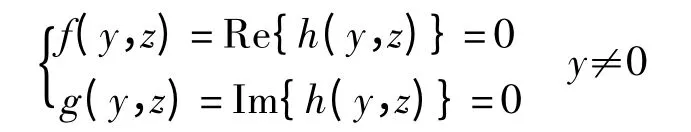
其中:f(y，z)有30 項，最高次數是7;g(y，z)有29項，最高次數是7.通過計算可得參數取任意值時該系統均無實根.

因此，當參數滿足R1= β － μ － r ＞0 時，式(10)系統在平衡點處全時滯穩定.

5 結 論

本文在Gr?bner 基、三角化分解和實解分類等符號計算原理基礎上提出了一種新的驗證生物系統全時滯穩定性的算法.

1)經實驗驗證表明該算法可實現較為優異的計算性能，例如計算含有62 項的多項式所用時間僅僅為幾秒，這是傳統的數學計算所達不到的.

2)此外，仍在進行任意多時滯微分系統的全時滯穩定性分析的算法研究及實驗.

References)

［1］ 秦元勛.有時滯的系統的無條件穩定性［J］.數學學報，1960，10(1):125-142.

Chin Y S.Unconditional stability of systems with time lags［J］.Acta Mathematica Sinica，1960，10(1):125-142(in Chinese).

［2］ 秦元勛，俞元洪.一類時滯微分系統無條件穩定的條件［J］.控制理論與應用，1984，1(1):23-35.

Chin Y S，Yu Y H.Unconditional stability conditions for a class of differential systems with time delay［J］.Journal of Control Theory and Applications，1984，1(1):23-35(in Chinese).

［3］ 周超順，鄧聚龍.線性定常時滯系統全時滯漸近穩定的充分代數判據［J］.自動化學報，1990，16(1):62-65.

Zhou C S，Deng J L.A sufficient algebra criteria for stability of linear constant time-delay system［J］.Acta Automatica Sinica，1990，16(1):62-65(in Chinese).

［4］ Cao D Q，He P，Ge Y M.Simple algebraic criteria for stability of neutral delay-differential systems［J］.Journal of the Franklin Institute，2005，342(3):311-320.

［5］ Hu G D，Hu G D，Cahlon B.Algebraic criteria for stability of linear neutral systems with a single delay［J］.Journal of Computational and Applied Mathematics，2001，135(1):125-133.

［6］ He P，Cao D Q.Algebraic stability criteria of linear neutral systems with multiple time delays［J］.Applied Mathematics and Computation，2004，155(3):643-653.

［7］ Niu W，Wang D.Algebraic analysis of bifurcation and limit cycles for biological systems［M］.Berlin，Heidelberg:Springer，2008:156-171.

［8］ Niu W，Wang D.Algebraic approaches to stability analysis of biological systems［J］.Mathematics in Computer Science，2008，1(3):507-539.

［9］ Wang D.Elimination methods［M］.Berlin，Heidelberg:Springer，2001:193-224.

［10］ Buchberger B.Gr?bner bases:An algorithmic method in polynomial ideal theory［J］.Multidimensional Systems Theory，1985:184-232.

［11］ Faugère J C.A new efficient algorithm for computing Gr?bner bases (F4)［J］.Journal of Pure and Applied Algebra，1999，139(1):61-88.

［12］ Yang L，Xia B.Real solution classification for parametric semialgebraic systems［C］∥Algorithmic Algebra and Logic［S.l.:s.n.］，2005:281-289.

［13］ 宋永利，韓茂安，魏俊杰.多時滯捕食-食餌系統正平衡點的穩定性及全局Hopf 分支［J］.數學年刊:A 輯，2005，25(6):783-790.

Song Y L，Han M A，Wei J J.Stability and global Hopf bifurcation for a predator-prey model with two delays［J］.Chinese Annals of Mathematics:Series A，2005，25(6):783-790(in Chinese).

［14］ Bhattacharyya S P，Chapellat H，Keel L H.Robust control-the parametric approach［M］.New York:Prentice Hall PTR，1995:446-472.

［15］ Lancaster P，Tismenetsky M.The theory of matrices:With applications［M］.Pittsburgh:Academic Press，1985:89-103.

［16］ Xia B.DISCOVERER:A tool for solving semi-algebraic systems［J］.ACM Communications in Computer Algebra，2007，41(3):102-103.

［17］ Kar T K，Pahari U K.Non-selective harvesting in prey-predator models with delay［J］.Communications in Nonlinear Science and Numerical Simulation，2006，11(4):499-509.

［18］ Cooke K L.Stability analysis for a vector disease model［J］.Journal of Mathmatics，1979，9(1):31-42.

［19］ Meng X，Chen L，Wu B.A delay SIR epidemic model with pulse vaccination and incubation times［J］.Nonlinear Analysis:Real World Applications，2010，11(1):88-98.