改進的模擬溫補晶振寬溫補償方法

韓艷菊，楊科 ，鄭鴻耀

(1.北京航空航天大學 電子信息工程學院，北京100191; 2.北京無線電計量測試研究所，北京100854)

模擬溫補晶體振蕩器(簡稱模擬溫補晶振)是一種利用模擬溫度補償電路補償頻率隨溫度變化，從而在較寬的溫度范圍內保持良好頻率穩定度的晶體振蕩器［1］，具有低功耗和低噪聲等特點.通常，模擬溫補晶振的溫度補償電路為電阻溫度補償網絡.對于如何提高模擬溫補晶振的頻率溫度穩定性，國內外開展了大量研究，提出了各種改進的溫度補償方法［2-7］.隨著集成電路的發展，又出現了集成式模擬溫補晶振和集成式數字溫補晶振.其中，集成式模擬溫補晶振內部集成了三次函數發生器，可根據環境溫度模擬產生補償電壓以補償頻率變化;集成式數字溫補晶振內部集成了存儲器或微處理器，可根據溫度變化查表或計算補償電壓以補償頻率變化［8-12］.這兩種溫補晶振都有效縮小了晶振體積，頻率溫度穩定性好，但其相位噪聲遠不能達到采用電阻補償網絡的模擬溫補晶振水平.例如，對于10 MHz 頻率，集成式模擬溫補晶振的相位噪聲僅能達到－140 dBc/Hz@1 kHz，集成式數字溫補晶振更差;而使用電阻補償網絡方法，相位噪聲可以達到－157 dBc/Hz@1 kHz［13-15］.同時，在短期頻率穩定度上，使用電阻補償網絡優于使用函數發生器或數字存儲器和數字處理器.并且，集成晶振的輸出多為方波，高頻頻譜分量豐富，不利于設備的電磁兼容性設計，集成芯片的耐輻照能力也較分立模擬器件差.因此，在對頻率穩定度和相位噪聲要求很高的儀器儀表、雷達、通信、導航等多個領域，采用電阻補償網絡的模擬溫補晶振依然得到廣泛應用，尤其是在空間工程中仍大量使用.

目前，對于采用電阻補償網絡的模擬溫補晶振，當要求工作在－40 ～+70℃或者更寬的溫度范圍內，且頻率溫度穩定性要達到±1 ×10－6時，一次溫度補償的成功率較低.一般首次安裝溫度補償網絡后，還需再經過2 ～3 次網絡參數調節才能使晶體振蕩器的頻率溫度穩定性滿足指標要求，既降低生產效率，又影響產品可靠性.對此，本文針對一次補償成功率低的問題，分析了影響溫度補償效果的因素，并在此基礎上提出改進的溫度補償方法［16］.

1 模擬溫補原理及分析

1.1 模擬溫補晶振工作原理

采用電阻溫補網絡的模擬溫補晶振由振蕩電路、變容二極管和電阻溫補網絡3 個部分組成，如圖1 所示.其中，電阻溫補網絡常采用橋式網絡型式，由負溫度系數熱敏電阻和固定電阻構成.

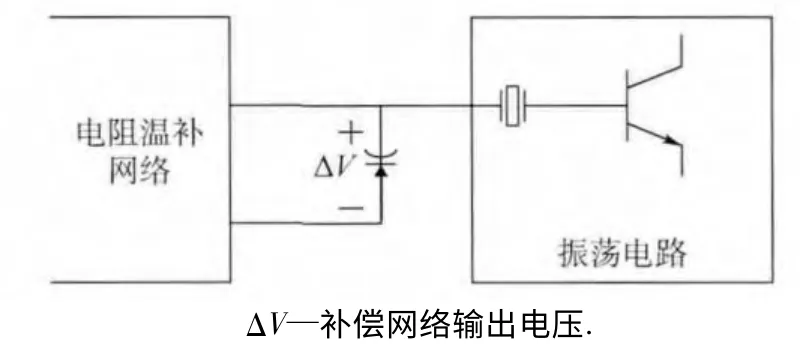
圖1 模擬溫補晶振工作原理框圖Fig.1 Analog TCXO working principle block diagram

工作時，溫補網絡產生與晶體振蕩器溫頻曲線形狀相反的電壓溫度曲線，并將其施加到變容二極管上，調節振蕩頻率使發生恰好反向于溫頻特性的變化，從而實現溫度補償，如圖2 所示.

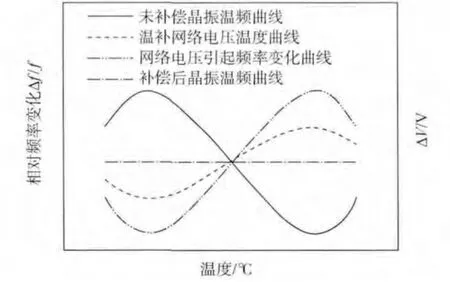
圖2 模擬溫度補償原理Fig.2 Analog temperature compensation principle

因此，溫度補償的關鍵就是通過補償網絡計算程序確定一組電阻值，使補償網絡的實際發生電壓與理想補償電壓之間的擬合誤差最小.

1.2 溫補精度影響因素分析

傳統溫度補償方法一次成功率低，主要是由于補償網絡計算程序中熱敏電阻模型不精確.

傳統補償方法中，熱敏電阻在窄溫范圍內測試，并使用式(1)進行建模.

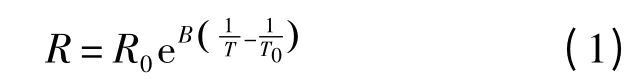
式中:T0和T 為絕對溫度，T0=298.15 K，T 為當前溫度;R0為T0時的電阻值;B 為材料常數.

當溫度范圍很寬時，式(1)中的計算模型不適用，而應如式(2)所示.

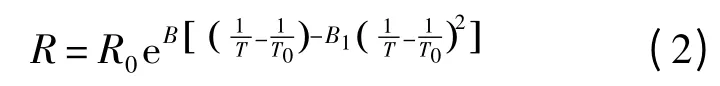
式中:B1為高階材料常數［17］.

此外，傳統方法中熱敏電阻溫度特性是在近似零功率條件下測量并計算或擬合得到的.實際上，熱敏電阻在溫補網絡中工作時并不能很好地滿足零功率條件.由于熱敏電阻具有耗散系數，因此消耗在熱敏電阻中的能量會引起溫升導致電阻值改變.而且，電路中還有其他器件或多或少的輻射熱量，引起溫度梯度.因而，熱敏電阻的計算模型和實際使用情況存在較大差距.如果將式(1)的熱敏電阻模型代入溫補網絡計算程序，必然引起大的誤差，造成實際補償效果惡化.

2 改進的溫度補償方法

新的模擬溫補晶振寬溫補償方法從熱敏電阻建模和補償網絡計算程序兩個方面進行改進.

2.1 熱敏電阻建模

改進溫度補償方法中，熱敏電阻采用在線測量和比例建模的方式.

首先，熱敏電阻測量中使用與補償網絡相同的電路形式和大致相當的電路參數，以及寬溫測試范圍，即盡量接近其實際使用情況，而非在零功率和窄溫條件下測量，如圖3 所示.其中，電阻符號上帶箭頭的為熱敏電阻(R4、R5、R7)，其余為固定電阻(R1～R3、R6、R8).

其次，在測試過程中，隨溫度變化，記錄圖3中各節點電壓.對于N 個溫度測試點，Vz、V1、V2、V3、V4均為N 維行向量.

然后，根據節點電壓和基爾霍夫定律、諾頓定律計算得到各熱敏電阻隨溫度變化的電阻值，并將熱敏電阻值表示為N 維向量R1×N.

圖3 熱敏電阻在線測量網絡Fig.3 On-line test network for thermistors

最后，將得到的熱敏電阻向量代入溫補網絡計算程序中使用.實際上，考慮到同批次熱敏電阻具有較好的一致性和工程應用的簡便性，可以采用熱敏電阻比例建模的方式.不必每只待使用的熱敏電阻都按圖3 進行實際測量，而是將上述測試完成的熱敏電阻作為參考熱敏電阻，其余相同類型、阻值相近的熱敏電阻建模為

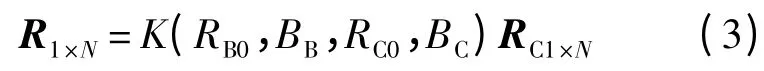
式中:K(RB0，BB，RC0，BC)為與待使用熱敏電阻和參考熱敏電阻特性參數相關的比例系數;RB0和BB為待使用熱敏電阻特性參數;RC0和BC為參考熱敏電阻特性參數，均可由傳統測試方法得到或廠家給出;RC1×N為參考熱敏電阻實測值，R1×N和RC1×N均為N 維行向量.

2.2 補償網絡計算程序

將式(3)建模的熱敏電阻代入溫補網絡計算程序中.溫補網絡輸出電壓ΔV 為N 維行向量，由圖3 可得

V1、V2和ΔV 的第k 個分量表達式為

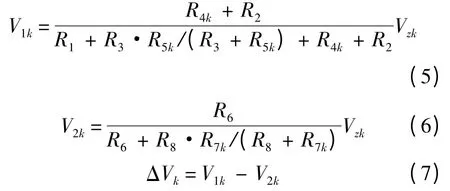
可見，V1、V2和ΔV 均為各電阻值的非線性函數.

使振蕩器溫頻特性得到完全補償的網絡電壓為目標補償電壓ΔM，N 維行向量.改進方法中，溫補網絡計算程序采用遺傳算法，通過優化計算求得一組網絡參數值，使網絡實際輸出電壓ΔV與目標補償電壓ΔM 之間的擬合誤差最小.

在算法中，染色體編碼采用實數編碼，將固定電阻值或固定電阻值和待使用熱敏電阻特性參數RB0、BB作為基因，依次排列構成染色體.

為了增強程序的實用性，目標函數包括3 部分:殘差平方和、最大偏差和常溫頻率準確度.這3 部分通過罰函數來折中［18］.

殘差平方和表達式為

最大偏差表達式為

常溫頻率準確度的表達式為

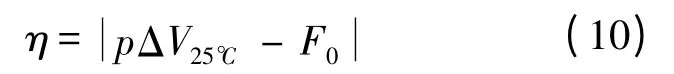
式中:p 為壓控靈敏度;ΔV25℃為25℃時補償網絡輸出電壓;F0為振蕩器標稱頻率.

在計算過程中通過選擇、交叉、變異等步驟，得到進化的染色體.并且，為了克服進化過程中的早熟和欺騙問題，獲得最佳結果，根據進化的不同階段，設置不同的群體選擇壓力，并實施最優保存策略［19］.

3 驗證試驗

3.1 熱敏電阻計算

根據熱敏電阻在線測量和比例建模方法，分別將2 組各3 只熱敏電阻連接到圖3 的測量網絡中，在－40 ～+70℃范圍內進行測量.

然后，將第1 組中的3 只熱敏電阻作為對應網絡位置的參考熱敏電阻.將第2 組的3 只熱敏電阻分別按照式(3)進行建模計算，建模計算值與其實測值和傳統方法計算值的比較結果如圖4所示.

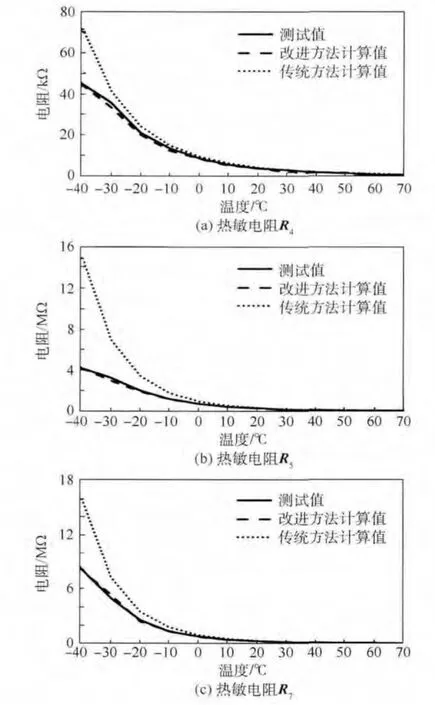
圖4 熱敏電阻計算值與測試值比較Fig.4 Comparison between compute values and test value of thermistor

由圖4 可見，相比于傳統方法，采用改進溫度補償方法計算得到熱敏電阻值更接近于實測值.因此，將該計算值代入溫補網絡計算程序可以有效提高計算準確度.

3.2 補償網絡參數計算

選取10 只10 MHz 晶體振蕩器進行溫度補償.要求補償后的晶體振蕩器在－40 ～+70℃的范圍內頻率溫度穩定性達到±1 ×10－6.

首先，選取10 組熱敏電阻，分別按式(3)進行建模，其中參考熱敏電阻與第3.1 節中參考熱敏電阻相同.

然后，將建模的熱敏電阻代入溫補網絡計算程序，并將待計算的固定電阻值按順序排列，組成實數編碼的染色體.在進化過程中，采用隨進化代數變化的交叉概率pc和變異概率pm.

目標函數表示為

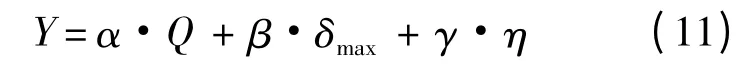
式中:α、β、γ 分別為Q、δmax和η 的權重.

迭代計算過程如圖5 所示，經過多次迭代計算達到收斂條件后，便得到一組最優的固定電阻值.為了進一步優化計算結果，計算程序中也可以將固定電阻和熱敏電阻特性參數RB0和BB同時作為待優化量進行實數編碼和優化計算.

圖5 補償網絡計算程序迭代過程Fig.5 Iteration process of compensation network computing program

3.3 頻率溫度穩定性測試

根據溫補網絡計算程序得到的固定電阻值，安裝溫補網絡.由于計算程序得出的電阻值通常為幾kΩ ～幾百kΩ 的任意實數，而實際電阻值為一系列離散值.因此，安裝時為了盡量接近計算值，網絡中每一個計算電阻由兩個實際電阻組合而成，并且組合精度不應低于1%.

將裝配完的10 只晶體振蕩器放入溫箱，進行頻率溫度穩定性測試，測試結果如表1 所示.表1中同時給出了采用傳統補償方法進行計算和裝配后的實測結果.

表1 傳統方法與改進方法測試結果對比Table 1 Results comparison between traditional method and modified method

可見，采用改進方法，10 只晶振進行一次溫度補償后，頻率溫度穩定性均達到并優于±1 ×10－6.以3 號晶體振蕩器為例，分別采用傳統方法和改進方法進行一次溫度補償后，得到頻率溫度穩定性如圖6 所示.補償前3 號晶體振蕩器的頻率溫度穩定性約為±15 ×10－6.

圖6 3 號晶振一次溫度補償結果Fig.6 Result of once temperature compensation for oscillator No.3

綜合表1 和圖6 表明，采用改進方法進行一次溫度補償的效果明顯優于傳統方法，不僅頻率波動大大減小，而且常溫下的頻率準確度也明顯提高.因此，改進方法可顯著提高晶體振蕩器的一次溫度補償成功率.

4 結 論

綜上所述，本文提出了一種改進的模擬溫補晶振寬溫范圍溫度補償方法.

1)改進方法中，熱敏電阻采用在線測試和比例建模，并將建模的熱敏電阻代入溫補網絡計算程序，提高了補償網絡參數計算的準確度.

2)溫補網絡計算程序中，通過遺傳算法優化獲得網絡參數解.該算法可適用多種復雜約束條件，且不依賴于初始解，因此使用靈活.

3)經試驗驗證，該方法可以有效提高溫度補償精度和一次溫補成功率，避免多次補償帶來的人員和設備占用，以及引入的不確定因素，因此可顯著提升生產效率和產品可靠性.

致謝 感謝劉宇婧和邢樹來同志在項目研究過程中給予的支持和幫助.

References)

［1］ GJB 1648A—2011.晶體振蕩器通用規范［S］.北京:總裝備部軍標出版發行部，2011:47.GJB 1648A—2011.General specification for crystal oscillators［S］.Beijing:General Armament Department Military Standard Publishing Department，2011:47(in Chinese).

［2］ John R V.Introduction to quartz frequency standards，ADA248503［R］.NJ:US Army LABCOM ETDL，1992:22-28.

［3］ 吳劍強.小型超寬溫度范圍模擬溫補晶振［J］.湖南大學學報，1993，20(6):34-38.

Wu J Q.The miniature temperature compensation crystal oscillator for ultra-wide range of temperature［J］.Journal of Hunan University，1993，20(6):34-38(in Chinese).

［4］ 靳寶安，袁桃利，賈玉霞.晶振溫補網絡研究［J］.陜西科技大學學報，2005，23(3):81-85.

Jin B A，Yuan T L，Jia Y X.Analyse and research on the temperature compensate net of crystal oscillator［J］.Journal of Shaanxi University of Science ＆ Technology，2005，23(3):81-85(in Chinese).

［5］ 鄧敏，陳衛.寬溫高穩定度的溫度補償技術［J］.電訊技術，2008，48(6):44-46.

Deng M，Chen W.Temperature compensation technology with wide temperature and high frequency stability［J］.Telecommunication Engineering，2008，48(6):44-46(in Chinese).

［6］ 李建文，祖兵.高準確度寬溫石英晶振熱敏網絡溫度補償［J］.傳感器技術，2004，23(5):68-71.

Li J W，Zu B.Temperature compensation to quartz crystal oscillator by thermistor net with high accuracy within wide temperature scope［J］.Journal of Transducer Technology，2004，23(5):68-71(in Chinese).

［7］ 黃顯核.最佳逼近法在晶體頻溫曲線擬合和TCXO 中的應用［J］.壓電與聲光，2005，27(4):452-454.

Huang X H.Application of the best approximation algorithms on frequency-temperature curve fit and TCXO［J］.Piezoelectrics and Acoustooptics，2005，27(4):452-454(in Chinese).

［8］ Mi Z，Wei X C.A 0.1 ppm successive approximation frequencytemperature compensation method for temperature compensated crystal oscillators (TCXO)［C］∥Proceedings of 2009 World Congress on Computer Science and Information Engineering.Piscataway，NJ:IEEE Press，2009:493-498.

［9］ Wei F，Xian H H，Feng T，et al.An improved microcontroller compensated low phase noise overtone TCXO［C］∥Proceedings of 2009 IEEE International Frequency Control Symposium and the 22nd European Frequency and Time forum.Piscataway，NJ:IEEE Press，2009:974-977.

［10］ 孫敏，黎敏強，陳中平，等.一種寬溫高精度溫補晶振的研制［J］.電子技術，2013，26(8):90-92.

Sun M，Li M Q，Chen Z P，et al.A high precision temperature compensated crystal oscillator in wide temperature range［J］.Electronic Science and Technology，2013，26(8):90-92(in Chinese).

［11］ 江玉潔，陳辰，伏全海，等.一種全集成化的溫補晶體振蕩器［J］.宇航計測技術，2003，23(3):52-57.

Jiang Y J，Chen C，Fu Q H，et al.A full-integrated temperature compensated crystal oscillator［J］.Journal of Astronautic Metrology and Measurement，2003，23(3):52-57(in Chinese).

［12］ 尹紅斌.基于模擬-數字相結合的新型溫補晶振的產業化設計［D］.西安:西安電子科技大學，2007.

Yin H B.Industrialized research of temperature compensated crystal based on analog-digital method［D］.Xi’an:Xi’an Eletronic Science and Technology University，2007(in Chinese).

［13］ 王艷，黃顯核，閻立群，等.高精度低噪聲集成溫度補償晶體振蕩器［J］.壓電與聲光，2010，32(6):909-911.

Wang Y，Huang X H，Yan L Q，et al.An integrated temperature compensated crystal oscillator with high-precision and low-noise［J］.Piezoelectrics and Acoustooptics，2010，32(6):909-911(in Chinese).

［14］ Asad A A.Phase noise and jitter in CMOS ring oscillators［J］.IEEE Journal of Solid-State Circuits，2006，41(8):1803-1816.

［15］ Behzad R.A study of phase noise in CMOS oscillators［J］.IEEE Journal of Solid-State Circuits，1996，31(3):331-343.

［16］ 韓艷菊，楊科，鄭鴻耀.一種用于模擬溫度補償晶體振蕩器的溫度補償方法:中國，201310739925.3［P］.2013-12-30.

Han Y J，Yang K，Zheng H Y.A temperature compensation method for analog temperature compensated crystal oscillator:China，201310739925.3［P］.2013-12-30(in Chinese).

［17］ 趙聲衡，趙英.晶體振蕩器［M］.北京:科學出版社，2008:316-322.

Zhao S H，Zhao Y.Crystal oscillator［M］.Beijing:Science Press，2008:316-322(in Chinese).

［18］ 孫艷豐，鄭加齊，王德興，等.基于遺傳算法的約束優化方法評述［J］.北方交通大學學報，2000，24(6):14-19.

Sun Y F，Zheng J Q，Wang D X，et al.A survey of constraint optimization method based on genetic algorithm［J］.Journal of Northern Jiaotong University，2000，24(6):14-19(in Chinese).

［19］ 呂善偉，韓艷菊，王偉.遺傳算法綜合陣列的幅度和相位方向圖［J］.北京航空航天大學學報，2005，31(9):1014-1017.

Lü S W，Han Y J，Wang W.Synthesis of the array’s amplitude and phase pattern using genetic algorithm［J］.Journal of Beijing University of Aeronautics and Astronautics，2005，31(9):1014-1017(in Chinese).