基于Pair Copula的隨機潮流三點估計法

吳 巍 汪可友 韓 蓓 李國杰

(電力傳輸與功率變換控制教育部重點實驗室(上海交通大學) 上海 200240)

?

基于Pair Copula的隨機潮流三點估計法

吳 巍 汪可友 韓 蓓 李國杰

(電力傳輸與功率變換控制教育部重點實驗室(上海交通大學) 上海 200240)

現有Copula等方法難以對多維風電功率準確建模，且傳統的點估計法無法直接應用于風電功率具有相關性的場合。針對這一問題，提出基于Pair Copula和概率積分變換的隨機潮流點估計法。首先采用Pair Copula對多維風電功率進行建模，然后使用點估計法在獨立正態概率空間中采樣，最后，依據概率積分變換，把采樣點變換到實際風電功率的概率空間中進行潮流計算，從而使點估計法能夠處理具有任意概率分布的多維風電功率。對澳大利亞多個風電場出力樣本的建模和分析驗證了Pair Copula模型的優越性，基于IEEE 118節點系統的算例驗證了所提方法的有效性。

Pair Copula 多維相關性 概率積分變換 點估計法 隨機潮流

0 引言

截止到2013年底，中國風能裝機容量已達到91.4 GW[1]，大量風電場接入到電力系統中。與傳統發電形式相比，由于自然因素(風速)固有的隨機性和波動性，風電功率呈現較強的間歇性。另外，由于風電場之間的復雜空間位置關系，風電場出力之間呈現多樣化的相關特性[2]。風電功率的這些特性會對電力系統運行造成一定影響[3]，因此在對電力系統進行隨機潮流(probabilistic load flow，PLF)計算和運行特性分析時，需綜合考慮多風電場風電功率的概率特性。

自1974年B.Borkowska[4]提出PLF的概念以來，國內外學者提出了多種隨機潮流計算方法。其中，蒙特卡羅法[5，6](Monte Carlo simulation，MCS)計算準確度高，但即使提高采樣效率，計算量仍然較大，一般作為驗證其他方法準確度的標準。解析法[7]基于單一運行點，對潮流方程進行線性化，這會引入一定誤差[8]。點估計法[9](point estimate method，PEM)無需知道輸入和輸出之間具體的函數關系表達式，僅通過少量確定性計算，即可得到較高準確度的輸出變量統計量，但點估計法需要假設輸入隨機變量相互獨立，無法處理風電功率具有相關性的情況。

目前，考慮輸入變量相關性的PLF方法，主要關注兩方面內容：①對相關性隨機變量的準確建模；②結合相關性概率模型，改進現有PLF方法，從而使其能處理隨機變量的相關性。

在相關性建模方面，文獻[10]提出三階多項式變換，采用線性相關系數表征隨機變量相關性。文獻[11]采用Spearman秩相關系數描述輸入隨機變量間的相關性。然而，隨機變量相關特性的完整表征方式是聯合概率分布，其具有諸多測度指標分別從不同方面考察相關特性，線性相關系數和秩相關系數只是諸多測度指標中的一部分[12]。因而上述方法不能完整地表征隨機變量的相關性。

Copula理論則是一種有效的聯合概率分布建模工具[13]，Nataf變換實際是Normal Copula[14]。已有的多種Copula函數能夠分別較好地描述各類二維相關性。然而，對于三維及以上維的隨機量，現有多維Copula函數[15]僅能使用單一類型的Copula函數，即僅能描述單一類型的相關性結構，因而難以對多維風電功率間可能存在的多樣化的相關性結構準確建模。另外，在多維Copula模型與現有PLF方法結合方面，目前僅有Normal Copula能夠與現有PLF方法結合使用[14]，因而概率建模的不準確會導致PLF計算誤差。

針對目前多維相關性風電功率難以準確建模和處理的問題，本文提出了基于Pair Copula和概率積分變換的隨機潮流點估計法。不同于現有多維Copula函數，Pair Copula針對隨機變量兩兩之間不同的相關特性，采用了相適應的多種類型的二維Copula函數進行描述，從而能對多維概率分布模型準確建模。概率積分變換依據隨機變量的聯合概率分布(cumulative distribution function，CDF)，將其變換到獨立正態概率空間中，從而使點估計法能較好地處理具有任意聯合概率分布的多維相關性風電功率，并進行PLF計算。最后，以澳大利亞風電場歷史數據和IEEE 118節點系統為例，驗證了所提方法的有效性。

1 基于Pair Copula 的風電功率相關性模型

1.1 Copula理論

Copula函數對隨機變量的邊緣分布和相關性分別進行建模，進而構建多元隨機變量的聯合概率分布，簡化了建模步驟，是描述隨機變量相依結構的有力工具[16]。Sklar定理奠定了Copula理論的基礎。

Sklar定理：記F是邊緣分布為F1，F2，…，Fn的隨機變量X=[X1，X2，…，Xn]的聯合概率分布函數。則存在一個Copula概率分布函數C，對任意X∈Rn有

F(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn))

(1)

目前常用的二元Copula函數有Archimedean-Copula函數簇和Ellipse-Copula函數簇兩類[12]。前者包括Gumbel-Copula、Clayton-Copula和Frank-Copula，后者包括Normal-Copula。這些函數各自具有不同的對稱性和尾部相關性等特性，能夠較好地對各類二元相關特性進行建模。

二維Copula函數的構建步驟如下：

1)確定隨機變量的邊緣分布。可以采用經驗分布或非參數密度估計[17]。

2)分別使用上述4種Copula函數對隨機變量進行擬合，使用極大似然估計法得到相應Copula函數的參數。

3)進行擬合優度檢驗，選擇最優Copula函數。在此采用文獻[18，19]推薦的Cramér-vonMises(CvM)距離進行擬合優度檢驗，CvM距離越小，則所建概率分布模型對風電功率的擬合效果越好。

1.2PairCopula模型

目前，文獻中多維風電功率建模方法包括基于線性和秩相關系數的建模，以及基于Copula函數的模型。其中，線性和秩相關系數只是相關性測度的一部分，實際上，還有尾部相關性等相關系數，因而，采用線性和秩相關系數難以全面反映相關特性，建模不準確。對于Copula函數，當面對三維及以上更高維隨機變量時，二維Archimedean-Copula函數簇難以拓展到多維，Ellipse-Copula函數簇只能描述特定相關特性，難以對多維風電功率準確建模[15]。

針對現有Copula函數難以對多維風電功率準確建模的難題，本文提出采用C藤PairCopula構建多風場風電功率的相關性模型。

PairCopula方法最早是K.Aas等[20]提出，是一種基于傳統Copula理論，靈活的多維概率分布構造方式，能較好地描述多維隨機變量間差異化的相關特性，從而實現較好的擬合效果。目前，PairCopula常用的結構包括C藤和D藤兩種結構，兩者建模準確度類似，其中，C藤結構更簡單，易于實現，因而在此采用C藤PairCopula，下文簡寫為PairCopula。n維Pair Copula結構圖圖1所示。

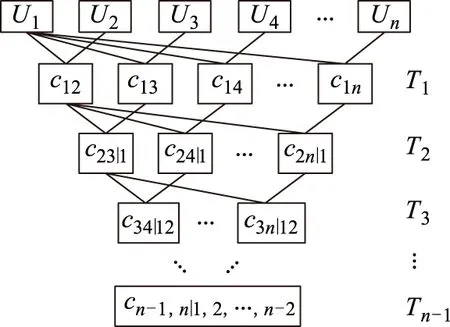
圖1 n維Pair Copula結構圖Fig.1 Structure diagram of n-dimensional Pair Copula

由圖1可見，n維Pair Copula有n-1層，Ti層有n-i個節點，其中第一個節點為根節點，與其余節點相連構造下一層的節點，通過逐層合并的方式構造多元概率分布。每個節點為一個二元Copula函數。

聯合概率密度f(x1，…，xn)為

(2)

式中，fi(xi)和Fi(xi)分別為Xi的概率密度函數(probabilistic distribution function，PDF)和CDF；c(·)為Copula的PDF，可表示為

c(u1,…,un)=?nC(u1,…,un)/(?u1…?un)

(3)

式中，ui=Fi(xi)，i=1，2，…，n。

依據Pair Copula理論[20]，c(·)可分解為二維Copula函數的乘積

(4)

式中

ci,j|1,…,i-1:=ci,j|1,…,i-1(F(ui|u1,…,ui-1),

F(uj|u1,…,ui-1))

(5)

式中，i=1時，ci，j|1，…，i-1為c1，j(u1，uj)。結合圖1和式(4)可以看到，Pair Copula中所有節點對應Copula函數的乘積即為式(4)。式(5)中條件分布性質為

(6)

(7)

Pair Copula把隨機變量兩兩合并，采用相應的二元Copula函數描述，能夠根據需要引入多種Copula函數來描述各類相關特性，使用靈活，適用范圍廣，從而可提高多維概率模型的擬合準確度。

1.3 Pair Copula建模方法

參照圖1，Pair Copula建模過程自上而下，采用1.1節中二維Copula函數最優擬合步驟，逐步估計出T1～Tn-1層中所有節點對應的二維Copula函數，從而確定Pair Copula。具體建模步驟如下：

1)基于風電功率X=[X1，X2，…，Xn]歷史數據，得到相應的邊緣概率分布Fi(xi)，i=1，2，…，n。

2)把X歷史數據帶入ui=Fi(xi)，得到均勻分布U=[U1，U2，…，Un]的樣本點。

3)基于U的樣本點，采用如下算法構建Pair Copula模型。

Forj=2，…，n

基于U1，Uj的樣本點，估計得到c1，j(u1，uj；θ1，j)；

計算v1,j=?C1,j(u1,uj)/?u1

Endfor

Fori=2，…，n-1

Forj=i+1，…，n

基于vi-1，i，vi-1，j的樣本點，估計得到ci，j|1，…，i-1(vi-1，i，vi-1，j；θi，j)

計算vi,j=?Ci,j|1,…,i-1(vi-1,i,vi-1,j/?vi-1,i)

Endfor

Endfor

其中，θ為Copula函數參數，vi，j=F(uj|u1，…，ui)。從而得到Pair Copula中所有節點對應的Copula函數。

4)基于式(4)，得到Copula PDF，令ui=Fi(xi)，得到風電功率概率模型，完成Pair Copula建模。

2 含風電的改進隨機潮流點估計法

2.1 隨機潮流問題

電力系統潮流方程為

(8)

(9)

式中，Pinj和Qinj分別為節點注入有功和無功功率；V和θ分別為節點電壓幅值和相角；Yij∠φij為系統導納矩陣第(i，j)個元素；K為系統節點數目。

實際電力系統中存在諸多隨機因素，如風電功率和負荷等，隨機潮流把這些不確定因素視作輸入變量，計算得到輸出變量(系統潮流和節點電壓)的概率特性，從而可以更全面地分析電力系統運行特性。

2.2 點估計法

點估計算法最早由H.P.Hong[9]于1998年提出，是一種分析隨機潮流等隨機響應問題的近似計算方法。點估計法利用輸入隨機變量的統計信息，構造特定的輸入隨機變量采樣點，針對這些采樣點，僅通過確定性計算少數次響應，即可得到輸出隨機變量的統計信息。

常用的2n+1點估計法要求隨機變量相互獨立。記xi的期望、標準差、偏度和峰度分別為λi，1、λi，2、λi，3和λi，4。點估計法前2n個采樣點中，每個采樣點僅一個分量分別選取2個采樣值，其余分量都取為對應期望值，采樣點為

Si,k=[λ1,1,…,λi,1+ξi,kλi,2,…,λn,1]
i=1,…，nk=1,2

(10)

式中

(11)

點估計法第2n+1個采樣點中，各分量為對應隨機量的期望值

S2n+1=[λ1,1,λ2,1,…,λn,1]

(12)

記h(·)為針對一個采樣點，進行確定性潮流計算得到的輸出樣本值，則輸出y的j階原點矩計算式為

(13)

式中權重系數為

(14)

得到輸出y的j階原點矩后，則期望μ和標準差σ為

(15)

2.3 隨機潮流的改進點估計法

實際電力系統運行中，風電功率具有相關性，如果忽略這種相關性，會帶來較大的計算誤差。由于點估計法要求輸入隨機量相互獨立，因此需要依據風電功率相關特性，對點估計法進行改進。

最準確描述輸入隨機量相關特性的模型是其聯合概率分布，而這可通過上文所述Pair Copula進行建模獲得。在此采用概率積分變換[21]，可把具有任意聯合CDF的輸入隨機變量，轉換到獨立標準正態分布的概率空間中。概率積分變換為

(16)

式中，Z=[z1，z2，…，zn]服從獨立標準正態分布；Ф-1為標準正態分布CDF的反函數。

此時，在獨立正態概率空間上，推導點估計法的采樣點，即式(16)中的Z，基于概率積分變換，將其轉換得到原始輸入隨機變量概率空間中的采樣點，并進行確定性潮流計算，即可得到輸出的各階矩。隨機潮流改進點估計法步驟如下：

1)基于1.3節Pair Copula建模步驟，對輸入隨機變量進行建模。

2)使用點估計法在獨立正態概率空間中進行采樣。相應的采樣點為

(17)

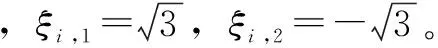
4)針對X的采樣點，計算得到相應的輸出量的樣本值。

5)依據式(18)計算得到輸出的各階矩。

(18)

3 仿真算例

3.1 Pair Copula模型驗證

以澳大利亞12個風電場2009年7月31日～2010年7月31日1h間隔的歷史數據[22]為例，驗證Pair Copula的有效性。按各自最大功率標幺化，分別記為P1，…，P12。由于樣本數足夠多，在此采用經驗分布獲得其邊緣概率分布。

首先，進行二維風電功率建模分析。分別采用Frank Copula和Normal Copula對U7和U8進行擬合，各Copula模型的散點圖和歷史數據的散點圖如圖2所示。由圖2a中可見，歷史數據的散點大多分布于45°斜率的直線附近，風電功率易同時較大或較小，具有明顯的相關性。圖2c與圖2a相比較，可以看到，Normal Copula有許多散點偏離了45°斜率的直線，因而對稱相關性的建模有一定偏差，另外，尾部相關性也有一定偏差。另一方面，可以看到，圖2b與圖2a的散點分布較為接近，因而Frank Copula擬合效果較好。

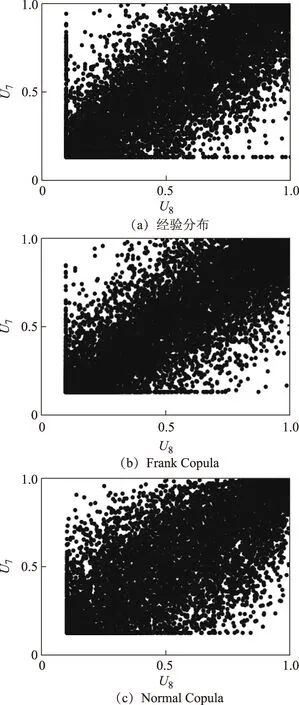
圖2 U7和U8的散點圖Fig.2 Scatter diagram of U7 and U8

對各二維風電功率，各Copula函數擬合的CvM距離如圖3所示。從圖3中可以看到，只有部分二維風電功率適于用Normal Copula建模，其余二維風電功率適用于Frank或Gumbel Copula建模，Clayton Copula誤差較大，不適于此算例。因而，針對不同的二維風電功率，應引入多種相適應的Copula函數進行建模，而不是僅僅使用單一的Normal Copula對風電功率進行建模。

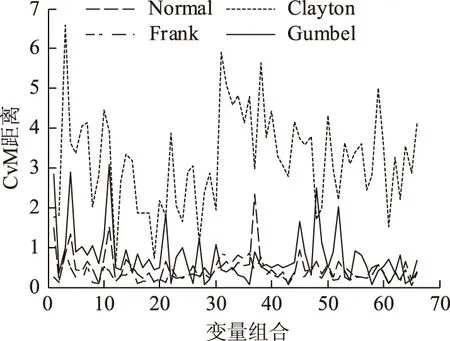
圖3 二維Copula函數CvM距離Fig.3 CvM distances of 2 dimensional Copula functions

然后，對所有風電功率建模，進行整體擬合效果檢驗，CvM距離及參數估計時間如表1所示，進行局部擬合效果檢驗，對所有6維風電功率組合檢驗得到的CvM距離如圖4所示。

表1 Normal Copula和Pair Copula的CvM距離及參數估計時間Tab.1 CvM distances and estimation time of Normal Copula and Pair Copula

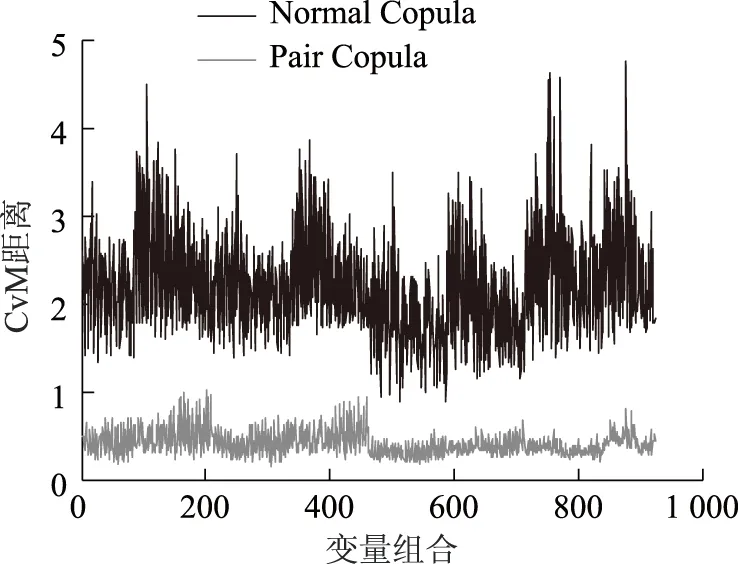
圖4 6維風電功率CvM距離Fig.4 CvM distances of 6 dimensional wind power outputs

由表1和圖4可知，Pair Copula的整體擬合CvM距離遠小于Normal Copula，擬合效果優于Normal。局部擬合檢驗中，Normal Copula的CvM距離始終較大，而Pair Copula的CvM距離則能保持在較低的值。這是由于Pair Copula中引入了多種Copula函數，可以描述各種類型的相關特性。因而，Pair Copula能同時實現最優的整體和局部擬合效果。

考察不同相關性模型的計算負擔。不同相關性模型與點估計法結合時，其潮流計算的計算量相同，不同的是建模和相關性處理(即配點轉換)的時間。其中，Normal copula配點轉換由于采用了Cholesky分解，僅涉及矩陣運算，計算很快。Pair Copula的配點轉換是把原始配點帶入解析式中進行計算，僅涉及代數運算，計算也很快[20]，與Normal Copula相近。因而，重點考慮建模的計算負擔。

理論上，Pair Copula建模估計的時間與節點數目(即(n2-n)/2)有關，單個節點的估計時間約為0.5 s，對于12維變量，建模時間約為(122-12)/2×0.5=33 s，與表1中結果一致。對于Normal copula，估計時間為0.14 s。這是由于Pair Copula需要對每個節點進行GOF檢驗，選取最優Copula類型導致的，從而獲取更高的建模準確度，而多元Normal Copula則不需要進行GOF檢驗和選型，且得到了Maltab的矢量化優化。另外，需要指出的是，在未來的工作中將研究truncated Pair Copula (tPC)，其在本文full Pair Copula (fPC)的基礎上對fPC做簡化，維持滿意的建模準確度，同時可以降低計算負擔，計算量可減少到約為(2n-3)×0.5[23]，從而對建模時間和準確度進行折中。

3.2 IEEE 118節點系統隨機潮流

采用IEEE 118節點系統[24]驗證本文模型在隨機潮流中的應用。IEEE 118節點系統有54臺發電機組，總裝機容量為9 966.2 MW，系統峰荷4 242 MW。12，31，46，54，80，87，103，111處的發電機分別替換為等容量的8個風場，剩余4個風場接入34，36，40，42節點，額定容量為50MW，風場全部采用恒壓控制。負荷有功服從獨立正態分布，均值為靜態平衡點處的值，標準差為均值的5%，負荷的功率因數恒定。

依據風電功率歷史數據計算得到的結果作為參考值，輸出變量期望和標準差的相對誤差如式(19)和式(20)所示。

(19)

(20)

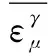
在進行PLF計算時，考慮現有文獻中PEM常用的兩種風電功率模型，分別為假設獨立的概率模型和Normal Copula[14]，與本文所提Pair Copula模型進行對比。對這三種風電功率模型分別進行PLF計算，計算結果如表2所示。

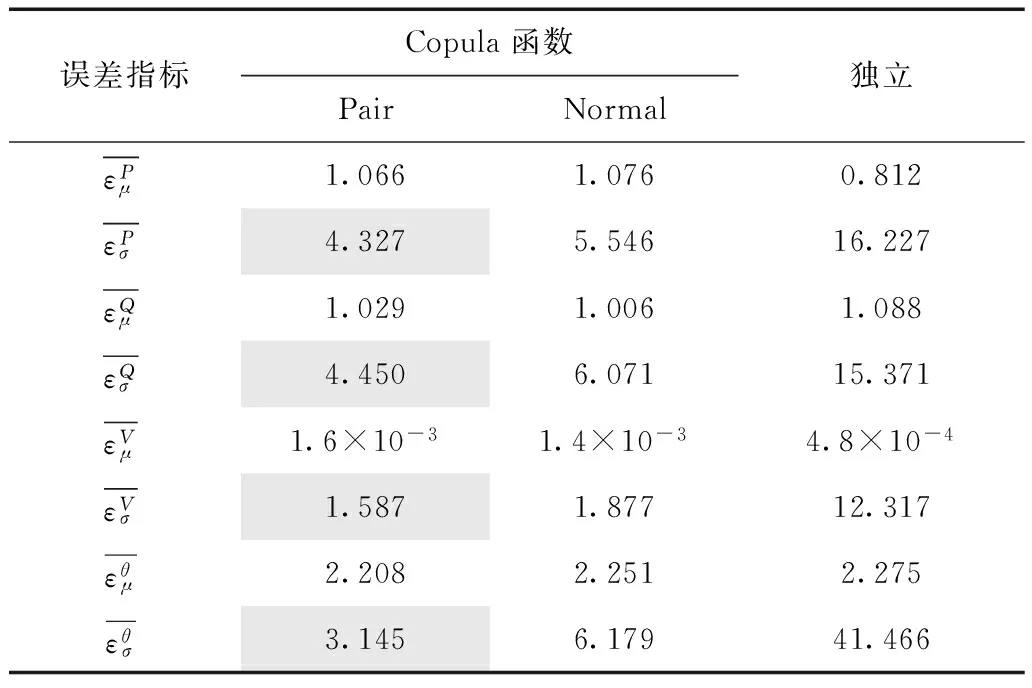
表2 IEEE 118節點系統平均相對誤差結果Tab.2 Average error indices of the IEEE 118-bus system (單位：%)

由表2可知，在不同風電功率模型下，對于期望的計算都能獲得較好的準確度，因而相關性對期望的影響較小。然而，在不同概率模型下，標準差的相對誤差具有比較大的差距。不考慮相關性時，PEM對于線路有功標準差的平均相對誤差高達16.227%，誤差較大。Normal Copula考慮了風電功率相關性，然而，由于其建模準確度不高，仍然具有一定的誤差。Pair Copula由于具有較高的建模準確度，其誤差最小。因而，在進行PLF計算時，是否考慮風電功率相關性以及風電功率建模的準確性對標準差的計算準確度具有顯著影響。

為了分析這一現象，在此借助半不變量法[7]的數學基礎進行分析。半不變量的數學基礎是潮流方程的近似線性化，輸出y表示為輸入xi的線性組合

(21)

由式(21)可得到期望E(y)

(22)

由式(22)可知，E(y)與輸入xi的期望有關，與相關性無關。因而，僅考慮各自的邊緣分布而不考慮相關性時，對于期望的計算影響較小。類似的，可得到方差D(y)

(23)

式中，ρij為xi、xj的相關系數。

與E(y)不同的是，D(y)不僅與D(xi)有關，即與邊緣分布有關，還與相關性有關，因而相關性對標準差的影響較大。

為了進一步考察本文所提方法的適用性，本文考察了不同負荷波動幅度下的誤差，計算結果如表3所示。可以看出，負荷波動幅度對誤差影響較小，誤差維持在較低的水平。

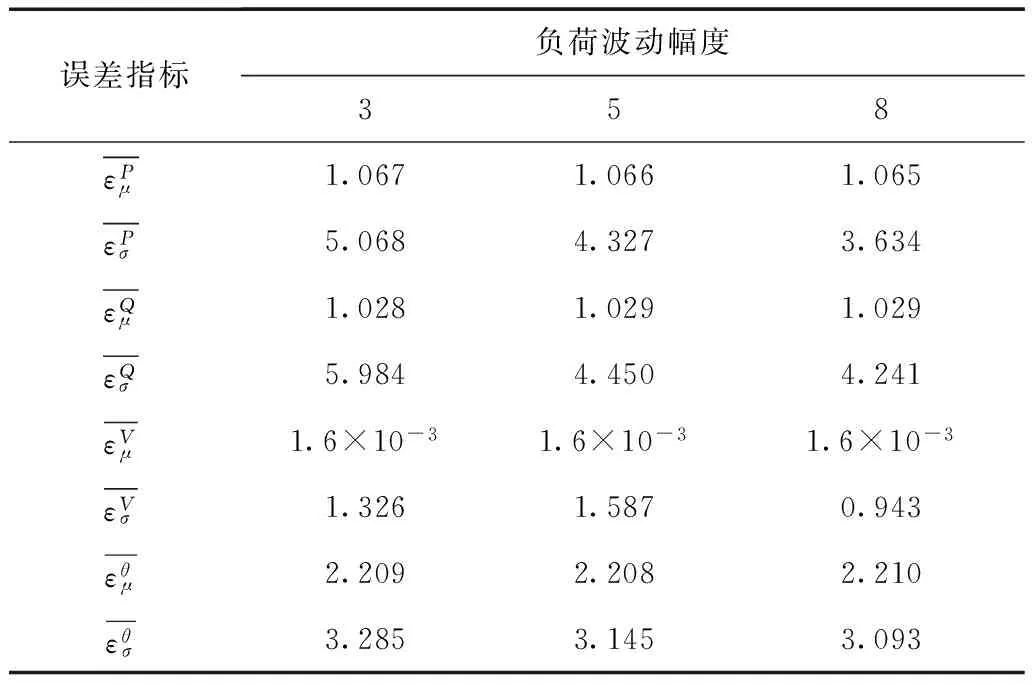
表3 不同負荷波動幅度時的平均相對誤差結果Tab.3 Average error indices under different fluctuations of load level (單位：%)

4 結論

針對PLF中，多維風電功率難以準確建模和處理的問題，本文提出了基于C藤Pair Copula和概率積分變換的隨機潮流點估計法。所提方法采用Pair Copula對多維風電功率概率分布進行建模，基于概率積分變換，將所建概率分布變換到獨立正態概率空間中，從而使點估計法能夠處理具有任意概率分布的相關性風電功率，具有較強的通用性。

多風電場歷史數據分析表明，相比于現有的Normal Copula模型，本文所建模型能夠更好地描述多維風電功率內部的相關特性，其概率分布的模型準確度更高。IEEE 118節點系統算例表明，忽略風電功率相關性會造成較大的誤差。同時，仿真結果驗證了所提改進隨機潮流點估計法的有效性和實用性，采用具有更高建模準確度的Pair Copula，能夠更準確地分析風電接入對電力系統的影響。

[1] Global Wind Energy Council(GWEC).Global Wind Report 2013-annual market update[EB/OL].2014-05-11.http：//www.gwec.net.

[2] Wan Y H，Milligan M，Parsons B.Output power correlation between adjacent wind power plants[J].Journal of Solar Energy Engineering，2003，125(4)：551-555.

[3] 蔣程，劉文霞，張建華，等.含風電接入的發輸電系統風險評估[J].電工技術學報，2014，29(2)：260-270. Jiang Cheng，Liu Wenxia，Zhang Jianhua，et al.Risk assessment of generation and transmission systems considering wind power penetration[J].Transactions of China Electrotechnical Society，2014，29(2)：260-270.

[4] Borkowska B.Probabilistic load flow[J].IEEE Transactions on Power Apparatus and Systems，1974，93(3)：752-759.

[5] 陳芳，張利，韓學山，等.配電網線損概率評估及應用[J].電力系統保護與控制，2014，42(13)：39-44. Chen Fang，Zhang Li，Han Xueshan，et al.Line loss evaluation and application in distribution network[J].Power System Protection and Control，2014，42(13)：39-44.

[6] 茆美琴，周松林，蘇建徽.基于風光聯合概率分布的微電網概率潮流預測[J].電工技術學報，2014，29(2)：55-63. Mao Meiqin，Zhou Songlin，Su Jianhui.Probabilistic power flow forecasting of microgrid based on joint probability distribution about wind and irradiance[J].Transactions of China Electrotechnical Society，2014，29(2)：55-63.

[7] 董雷，楊以涵，張傳成，等.綜合考慮網絡結構不確定性的概率潮流計算方法[J].電工技術學報，2012，27(1)：210-216. Dong Lei，Yang Yihan，Zhang Chuancheng，et al.Probabilistic load flow considering network configuration uncertainties[J].Transactions of China Electrotechnical Society，2012，27(1)：210-216.

[8] 朱星陽，劉文霞，張建華.考慮大規模風電并網的電力系統隨機潮流[J].中國電機工程學報，2013，33(7)：77-85. Zhu Xingyang，Liu Wenxia，Zhang Jianhua.Probabilistic load flow method considering large-scale wind power integration[J].Proceedings of the CSEE，2013，33(7)：77-85.

[9] Hong H P.An efficient point estimate method for probabilistic analysis[J].Reliability Engineering & System Safety，1998，59(3)：261-267.

[10]劉小團，趙晉泉，羅衛華，等.基于TPNT和半不變量法的考慮輸入量相關性概率潮流算法[J].電力系統保護與控制，2013，41(22)：13-18. Liu Xiaotuan，Zhao Jinquan，Luo Weihua，et al.A TPNT and cumulants based probabilistic load flow approach considering the correlation variables[J].Power System Protection and Control，2013，41(22)：13-18.

[11]徐瀟源，嚴正，馮冬涵，等.基于輸入變量秩相關系數的概率潮流計算方法[J].電力系統自動化，2014，38(12)：54-61. Xu Xiaoyuan，Yan Zheng，Feng Donghan，et al.Probabilistic load flow calculation based on rank correlation coefficient of input random variables[J].Automation of Electric Power Systems，2014，38(12)：54-61.

[12]蔡菲，嚴正，趙靜波，等.基于 Copula 理論的風電場間風速及輸出功率相依結構建模[J].電力系統自動化，2013，37(17)：9-16. Cai Fei，Yan Zheng，Zhao Jingbo.Dependence structure models for wind speed and wind power among different wind farms based on copula theory[J].Automation of Electric Power Systems，2013，37(17)：9-16.

[13]蔡德福，石東源，陳金富.基于Copula理論的計及輸入隨機變量相關性的概率潮流計算[J].電力系統保護與控制，2013，41(20)：13-19. Cai Defu，Shi Dongyuan，Chen Jinfu.Probabilistic load flow considering correlation between input random variables based on Copula theory[J].Power System Protection and Control，2013，41(20)：13-19.

[14]Zhang L，Cheng H，Zhang S，et al.A novel point estimate method for probabilistic power flow considering correlated nodal power[C].IEEE PES General Meeting|Conference & Exposition，National Harbor，MD，2014：1-5.

[15]Berg D，Aas K.Models for construction of multivariate dependence-a comparison study[J].The European Journal of Finance，2009，15(7)：639-659.

[16]Nelsen R B.An Introduction to Copulas[M].New York：Springer，1999.

[17]Soleimanpour N，Mohammadi M.Probabilistic load flow by using nonparametric density estimators[J].IEEE Transactions on Power Systems，2013，28(4)：3747-3755.

[18]Genest C，Rémillard B，Beaudoin D.Goodness-of-fit tests for copulas：a review and a power study[J].Insurance：Mathematics and economics，2009，44(2)：199-213.

[19]Berg D.Copula goodness-of-fit testing：an overview and power comparison[J].The European Journal of Finance，2009，15(7-8)：675-701.

[20]Aas K，Czado C，Frigessi A，et al.Pair Copula constructions of multiple dependence[J].Insurance：Mathematics and economics，2009，44(2)：182-198.

[21]Rosenblatt M.Remarks on a multivariate transformation[J].The Annals of Mathematical Statistics，1952，23(3)：470-472.

[22]Data[DB/OL].Sydney：AEMO，2010[2014-06-01].http：//www.oz-energy-analysis.org/data/generation_wind_farms.php.

[23]Brechmann E C，Czado C，Aas K.Truncated regular vines in high dimensions with application to financial data[J].Canadian Journal of Statistics，2012，40(1)：68-85.

[24]Power Systems Test Case Archive[DB/OL].Washington：University of Washington，1993[2014-11-01].http：//www.ee.washington.edu/research/pstca.

Pair Copula Based Three-point Estimate Method for Probabilistic Load Flow Calculation

WuWeiWangKeyouHanBeiLiGuojie

(Key Laboratory of Control of Power Transmission and Conversion， Ministry of Education Shanghai Jiao Tong University Shanghai 200240 China)

Current methods，such as Copula theory，are inadequate to model multiple dependent wind power outputs accurately.Moreover，the point estimate method cannot handle the correlation among wind power outputs.Thus，an improved point estimate method based on Pair Copula and probability integral transformation is proposed for probabilistic load flow studies.The probabilistic model of multiple correlated wind power outputs is firstly constructed by Pair Copula.The point estimate method is then used to generate samples in the independent normal domain.Finally，based on the probability integral method，the samples are transformed into the actual probabilistic domain in order to find the characteristics of the power system operation.In this way，the point estimate method can handle multiple dependent wind generations with arbitrary distributions.The modeling and analysis for the power outputs of adjacent wind farms in Australia verify the goodness-of-fit of Pair Copula.The probabilistic load flow of the IEEE 118-bus system is solved to demonstrate the effectiveness of the proposed method.

Pair Copula，multiple dependence，probability integral transformation，point estimate method，probabilistic load flow

國家高技術研究發展計劃(“863”計劃)(2014AA052003)，國家自然科學基金(51307107、51477098)，國家科技支撐計劃(2015BAA01B02)資助項目。

2014-12-29 改稿日期2015-02-14

TM315

吳 巍 男，1990年生，博士研究生，研究方向為微電網的安全穩定分析及優化運行。(通信作者)

汪可友 男，1979年生，博士，副教授，研究方向為電力系統分析與控制，新能源的不確定性分析。