基于端口阻抗的磁耦合諧振式無線電能傳輸特征參數(shù)仿真方法研究

毛世通 朱春波 宋 凱 魏 國 遲浩坤

(1.哈爾濱工業(yè)大學電氣工程及其自動化學院 哈爾濱 150001 2.中國海洋大學信息科學與工程學院 青島 266000)

?

基于端口阻抗的磁耦合諧振式無線電能傳輸特征參數(shù)仿真方法研究

毛世通1朱春波1宋 凱1魏 國1遲浩坤2

(1.哈爾濱工業(yè)大學電氣工程及其自動化學院 哈爾濱 150001 2.中國海洋大學信息科學與工程學院 青島 266000)

以單個自諧振線圈等效模型的端口阻抗及耦合線圈之間二端口網(wǎng)絡(luò)的等效模型為出發(fā)點，利用高頻有限元仿真軟件，結(jié)合無線電能傳輸技術(shù)自身的特點，提出分布參數(shù)諧振線圈仿真分析以及關(guān)鍵參數(shù)的提取方法，通過實驗對比驗證仿真方法的合理性。另外根據(jù)耦合線圈頻域阻抗分裂的特點提出耦合系數(shù)的計算方法，為進一步分析分布式參數(shù)線圈對無線電能傳輸性能影響的研究提供參考。

無線電能傳輸 磁耦合諧振 高頻有限元仿真 線圈參數(shù)提取

0 引言

近年來，無線電能傳輸技術(shù)由于其無需電線連接的新型電能供給特性而得到了廣泛關(guān)注。自2007年MIT的索爾加西克教授的研究小組提出基于磁耦合諧振式的近場無線電能傳輸?shù)母拍頪1]以來，這種利用線圈共振式的無線電能傳輸技術(shù)受到了廣泛關(guān)注，并且很多學者進行了更加深入的研究。目前，基于線圈諧振的無線電能傳輸系統(tǒng)的能量發(fā)射端和接收端大多是利用感應(yīng)線圈和電容構(gòu)成回路，通過自感線圈中存儲的磁場能量與電容中存儲的電場能量進行交換形成諧振腔體。根據(jù)耦合模理論，如果相互耦合的諧振體自諧振頻率相同，且同時能量供給源的頻率與線圈的自諧振頻率相同，將最大化彼此通過耦合交換的能量。所以線圈的諧振狀態(tài)將是無線電能傳輸系統(tǒng)工作性能的關(guān)鍵因素。

目前，關(guān)于近場耦合諧振式無線電能傳輸諧振線圈的構(gòu)成方式主要有兩種：①通過電線中的傳導(dǎo)電流激勵磁場，并利用集中式電容器存儲電場能量與線圈中的磁場能量相交換構(gòu)成諧振腔體；②通過線圈中的分布電感和分布電容構(gòu)成自諧振線圈的諧振腔體。

前者的特點在于：①線圈便于設(shè)計，可通過調(diào)整諧振電容器的電容值的大小來調(diào)整諧振體的固有頻率；可通過調(diào)整線圈匝數(shù)、大小以及形狀調(diào)整電感器的電感值，關(guān)于電感值的計算理論、經(jīng)驗公式都比較完備；②傳導(dǎo)電流會給線圈帶來熱損耗，尤其是在較高頻率下產(chǎn)生的趨膚效應(yīng)將導(dǎo)致這種損耗更加明顯；③集中式電容器內(nèi)存在介質(zhì)損耗，并且當品質(zhì)因數(shù)Q較高時將會在集中式電容器的兩端產(chǎn)生較大電壓。由于集中式電感和電容器所構(gòu)成的線圈系統(tǒng)的高頻損耗的存在，限制了其在高頻條件下的應(yīng)用。雖然能夠通過不同的電線材質(zhì)(如多股并繞線)，降低其趨膚效應(yīng)造成的損耗，但當頻率更高時(MHz級別)，其電磁行為以及內(nèi)部損耗的分析還尚不明確。盡管如此，這種集中參數(shù)線圈仍以其在低頻條件下的優(yōu)異性能在近距離以及大功率的無線電能傳輸?shù)膱龊系玫綇V泛應(yīng)用[2，3]，如非接觸變壓器[4]、電動汽車[5-7]無線充電技術(shù)以及無線傳感器無線供電[8]技術(shù)中。

后者的特點在于：①損耗低。根據(jù)文獻[1]，分布參數(shù)構(gòu)成的諧振線圈在10 MHz的品質(zhì)因數(shù)可達到2 500左右(實際在900以上)，這個量級的品質(zhì)因數(shù)是集中參數(shù)式的諧振線圈所無法達到的；②由于其可工作于高頻，所以基于分布參數(shù)的無線電能傳輸系統(tǒng)可工作于目前被廣泛認可的公共通信頻段內(nèi)(如ISM指出的6.78 MHz或13.56 MHz)；③線圈參數(shù)難于計算。由于線圈中的諧振腔體是由空間電流激磁所構(gòu)成的等效電感以及匝間電容所構(gòu)成的等效電容所產(chǎn)生，那么其諧振頻率以及品質(zhì)因數(shù)就難以計算得到。雖然可通過麥克斯韋方程組對空間電荷以及位移電流結(jié)合線圈結(jié)構(gòu)進行求解，但當線圈匝數(shù)較多，線圈形狀復(fù)雜，甚至線圈中含有鐵氧體結(jié)構(gòu)時，這種計算將會異常困難。由于分布參數(shù)的自諧振線圈相對于傳統(tǒng)的集中參數(shù)式線圈具有品質(zhì)因數(shù)高的特點，利用這種線圈進行無線電能傳輸?shù)募夹g(shù)依然受到重視[9-11]，并且應(yīng)用于例如筆記本電腦[12]以及體內(nèi)植入式醫(yī)療儀器[13-15]的無線充電的研究中。

值得注意的是，盡管有些研究將線圈固有頻率調(diào)節(jié)到較高等級(如MHz)，但將分布電容忽略且利用集中式電容進行調(diào)諧，那么這種線圈應(yīng)歸入第一種情況[16]。另外，有些研究盡管沒有在線圈中加入集中式諧振電容器，但其也沒有利用匝間電容建立諧振線圈，那么這種傳輸單純利用磁場感應(yīng)實現(xiàn)，不在下文的討論范圍之內(nèi)[17]。

針對分布參數(shù)的無線電能傳輸諧振線圈參數(shù)計算以及設(shè)計困難的問題，可借助于計算機的運算能力結(jié)合有限元(FEM)分析軟件對特定結(jié)構(gòu)的線圈進行仿真分析，以取代復(fù)雜繁瑣的空間微積分計算。但在目前研究中，如何利用仿真軟件得到自諧振線圈的有效參數(shù)，仍是亟待解決的問題。盡管一些研究提出了無線電能傳輸過程中的一些仿真結(jié)果，但其并沒有明確的參數(shù)提取方法的論述，難以與實際的傳輸系統(tǒng)相結(jié)合。

本文針對分布式參數(shù)的諧振線圈，基于線圈端口的等效電路結(jié)構(gòu)，結(jié)合有限元仿真軟件的計算結(jié)果，提出提取線圈等效電感、電容、內(nèi)阻以及諧振頻率和品質(zhì)因數(shù)的提取方法，并針對實際線圈進行測量對比。另外建立了耦合線圈的二端口阻抗網(wǎng)絡(luò)模型，根據(jù)頻域阻抗分裂的特性分析耦合系數(shù)的計算方法。通過這些研究，一方面可為基于分布參數(shù)的自諧振線圈設(shè)計提供參考，另一方面可為無線電能傳輸系統(tǒng)的整體分析提供重要的運算參數(shù)。

1 基于分布參數(shù)的單線圈仿真分析

應(yīng)用于無線電能傳輸發(fā)射端或接收端的典型的分布參數(shù)線圈如圖1所示，其等效電感以及等效電容為[18]

(1)

(2)

式中J(r)和ρ(r)分別為線圈r處微元dr的等效電流和電荷密度。這一原始定義表征了線圈中電感和電容的物理意義，但對特定結(jié)構(gòu)線圈參數(shù)計算來說缺乏一定的實用性。對于復(fù)雜電磁結(jié)構(gòu)的自諧振線圈來說，其匝間等效電容以及等效損耗電阻(介質(zhì)損耗和輻射損耗)缺乏足夠精確的經(jīng)驗公式，所以有限元分析(FEM)的數(shù)值計算方法成為分布參數(shù)線圈特征參數(shù)提取的最優(yōu)選擇。

圖1 典型的分布參數(shù)諧振線圈結(jié)構(gòu)

1.1 等效集中參數(shù)模型

為了能夠清晰地分析線圈在分布參數(shù)影響下的電磁行為，其等效的集中參數(shù)模型分析非常必要。需要指出的是，分布參數(shù)諧振線圈在全頻域的諧振頻率不惟一，即當激勵源的頻率改變時，自諧振線圈會出現(xiàn)多個諧振頻率點。對于基于近場諧振的無線電能傳輸應(yīng)用來說，由于其利用耦合場進行能量交換，必須避免振蕩頻率過高，導(dǎo)致波長接近于甚至小于傳遞距離以及線圈尺寸，所以在自諧振線圈的分析過程中應(yīng)選取最低的諧振頻率點附近的頻段建立集中參數(shù)模型。如果假設(shè)線圈兩端點為能量饋入端口的話，那么在相對低頻段成立的分布式參數(shù)自諧振線圈的等效集中參數(shù)電路[14]如圖2所示。

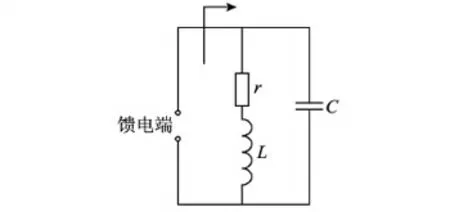
圖2 分布參數(shù)諧振線圈低頻段等效電路模型結(jié)構(gòu)

分布參數(shù)自諧振線圈等效電路從饋電端分析可等效為簡單的單端口網(wǎng)絡(luò)。進一步的，其等效的阻抗為

(3)

則當Im(Z(ω))=0時，可得到線圈諧振頻率為

(4)

式(4)中，諧振頻率可近似的前提是諧振線圈的品質(zhì)因數(shù)Q=ωL/r足夠高。

1.2 基于端口阻抗的參數(shù)計算方法

通過有限元軟件的端口激勵，對特定線圈模型可得到自諧振線圈單端口的等效阻抗曲線，如圖3所示。對于單個自諧振線圈來說，需要獲取諧振頻率以及品質(zhì)因數(shù)這兩個對傳輸系統(tǒng)影響最重要的參數(shù)，或獲得式(3)中的等效電感、電容以及內(nèi)阻進行計算。從曲線中可讀取Im(Z)=0的頻率點可直接獲得線圈的諧振頻率點。而對于線圈的品質(zhì)因數(shù)來說，需要對曲線進行進一步分析。這里由于參數(shù)模型結(jié)構(gòu)已知，可通過參數(shù)擬合的方法對仿真獲取的阻抗曲線進行擬合以獲得等效電路參數(shù)，再計算品質(zhì)因數(shù)。更便捷且體現(xiàn)物理意義的方法是通過尋找阻抗模衰減到3 dB時的頻率點，直接確定阻抗曲線的品質(zhì)因數(shù)，即

(5)

式中ω3dB+和ω3dB -分別為端口阻抗模衰減到3 dB時的頻率點，即

(6)

而線圈諧振時的阻抗模可通過仿真曲線直接讀取。其他參數(shù)計算可通過諧振頻率、品質(zhì)因數(shù)以及諧振阻抗計算得到

(7)

(8)

圖3 端口阻抗頻率響應(yīng)

1.3 分布參數(shù)線圈阻抗曲線仿真關(guān)鍵問題

有限元仿真方法對于無線電能傳輸線圈結(jié)構(gòu)以及耦合狀態(tài)的分析來說是非常理想的計算方法，但目前現(xiàn)有的與實際工程結(jié)合較好的仿真軟件都是針對某一特殊領(lǐng)域進行開發(fā)的，例如變壓器、電機或微帶傳輸線等。所以對于無線電能傳輸這種新興的電磁技術(shù)來說，不同的仿真軟件會有不同的計算效果。在仿真軟件的選擇中，要首先確定仿真軟件是否能考慮到目標系統(tǒng)的物理模型。對于集中式參數(shù)模型來說，其電場能量主要被儲存在集中電容器中，并可忽略位移電流，此時可選擇對于麥克斯韋全電流定律進行近似的仿真軟件。

而對于利用分布參數(shù)進行諧振的線圈來說，則必須考慮位移電流對線圈的影響。下文以高頻有限元仿真軟件HFSS為例簡單闡述仿真過程。 自諧振線圈仿真分析的最重要目的是獲得線圈的重要等效參數(shù)，其手段是通過迭代計算獲得線圈的端口阻抗曲線，進而通過上文所述的方法提取關(guān)鍵參數(shù)。仿真過程主要分為模型建立、端口激勵設(shè)置、邊界條件設(shè)置、分析過程設(shè)置以及后處理等。

與HFSS針對的應(yīng)用領(lǐng)域不同，無線電能傳輸技術(shù)在仿真設(shè)置上主要有3點值得注意的地方：①線圈端口設(shè)置應(yīng)以集中參數(shù)端口設(shè)置為主，以保證線圈的所有部分在求解域內(nèi)；②求解域(空氣包)的大小需要根據(jù)近場的衰減范圍決定。以HFSS為例，文獻[19]指出其空氣包尺寸至少大于1/4波長以保證計算準確度。 實際上應(yīng)用于近場耦合無線電能傳輸?shù)闹C振線圈相當于電小尺寸天線，即線圈尺寸小于工作頻率下的波長，也就是說頻率較低而線圈尺寸較小，如果仍保證1/4波長條件將會引發(fā)有限元軟件多尺度疊加(multi-scale)的問題。實際上求解域的尺寸在保證近場衰減3～4個數(shù)量級即可保證仿真結(jié)果的準確性；③根據(jù)之前的分析，掃頻范圍至少要包括阻抗參數(shù)衰減到其0.707倍的頻率范圍。

2 自諧振線圈參數(shù)計算對比實驗

下文以醫(yī)學應(yīng)用中的體內(nèi)植入式無線電能傳輸?shù)淖灾C振線圈為例，創(chuàng)建有限元仿真模型，同時比對實驗結(jié)果。

2.1 基于分布式參數(shù)的多層線圈(Multi-layer coil)

由于體內(nèi)植入式無線電能傳輸應(yīng)用的特點，電能接收端小型化是其最基本要求。由于線圈尺寸的限制，不能單純采用如圖1中的常規(guī)平繞式或螺線管式線圈結(jié)構(gòu)。一種更優(yōu)化的方式是多層平面螺旋線圈疊加的方法構(gòu)成自諧振線圈，并在加工方式上采用加工精度更高，設(shè)計過程更方便的印制電路板工藝構(gòu)建線圈。其空間結(jié)構(gòu)如圖4所示。

圖4 多層平面螺旋線圈結(jié)構(gòu)

仿真模型與實驗中諧振線圈均為圖4中的多層線圈壓制而成。圖4中FR- 4為構(gòu)成電路板為環(huán)氧樹脂和玻璃纖維結(jié)合的材料，這種材料相對介電常數(shù)為4.0～4.4，可有效增加匝間的寄生電容，降低自諧振頻率。實驗中應(yīng)用兩種不同線圈(Ⅰ型和Ⅱ型)，如圖5所示。

圖5 實驗中自諧振線圈

為了減少線圈輻射，降低頻率，在線圈的背部設(shè)計有調(diào)整其自諧振頻率的調(diào)諧銅片，如圖5所示。

2.2 仿真與實驗對比

實驗過程中，采用的Ⅰ型和Ⅱ型線圈分別根據(jù)單匝線圈的寬度設(shè)計了寬度w分別為1 mm、1.3 mm、1.5 mm的不同線圈。同時根據(jù)仿真獲得的阻抗曲線獲得自諧振線圈的諧振頻率以及品質(zhì)因數(shù)。根據(jù)圖5實驗線圈的尺寸與結(jié)構(gòu)，建立仿真模型，并根據(jù)2.3節(jié)所述設(shè)置端口激勵。線圈在近場的磁場分布如圖6所示。

圖6 根據(jù)實驗線圈進行仿真獲得的磁場分布結(jié)果

其阻抗曲線如圖7所示，其趨勢與圖3相類似。

根據(jù)阻抗曲線可提取出線圈在不同線徑寬度時的諧振頻率以及品質(zhì)因數(shù)，并與實驗結(jié)果相對比，如圖8所示。

圖8 線圈仿真結(jié)果與實驗結(jié)果比對

從圖8中可看出，仿真結(jié)果與實驗測量結(jié)果相近，基本可驗證仿真方法的準確性。其中仿真結(jié)果的諧振頻率以及品質(zhì)因數(shù)相比實驗結(jié)果來說相對較高，導(dǎo)致二者之間差異的原因主要有兩方面：①用于實驗的測量探頭與線圈端點之間存在接觸阻抗，在高頻情況下接觸阻抗帶來的影響將會非常明顯。其中接觸電阻降低了線圈的品質(zhì)因數(shù)，而接觸抗性(主要是容性)導(dǎo)致測量得到的諧振頻率較低；②仿真過程中影響仿真準確度的主要因素在于求解區(qū)域網(wǎng)格剖分的疏密程度，網(wǎng)格越密集計算準確度越高。尤其是在線圈模型的表面附近以及匝間網(wǎng)格剖分的密集程度直接影響寄生參數(shù)的計算準確度。但增加網(wǎng)格剖分(尤其是在線圈結(jié)構(gòu)復(fù)雜時)會增加運算器的計算負擔，所以有限元仿真計算的準確度受到計算機運算能力的制約。

3 耦合線圈的耦合系數(shù)分析

對于近場磁耦合諧振式無線電能傳輸系統(tǒng)中的諧振線圈來說，其本身的諧振頻率決定了系統(tǒng)的工作頻率，而根據(jù)耦合模理論[18]，其品質(zhì)因數(shù)與二者之間的耦合系數(shù)共同決定了傳輸效率。所以線圈之間的磁場耦合系數(shù)也是影響無線電能傳輸系統(tǒng)性能的關(guān)鍵參數(shù)。

3.1 耦合系統(tǒng)二端口阻抗分析

假設(shè)相互耦合的兩個線圈的自感分別為L1和L2，二者之間的互感為M，則耦合系數(shù)的定義為

(9)

基于分布參數(shù)的自諧振線圈在低頻段耦合模型如圖9a所示，其等效的二端口網(wǎng)絡(luò)模型如圖9b所示。

圖9 耦合線圈等效電路模型及其二端口模型

令V=(V1，V2)T，I=(I1，I2)T，則轉(zhuǎn)移阻抗為

(10)

根據(jù)近場諧振式無線電能傳輸性能最大化的基本要求，相互耦合的諧振線圈的諧振頻率應(yīng)一致，這里可假定相互耦合的線圈參數(shù)完全相同，即：L1=L2=L，C1=C2=C，ω1=ω2=ω0=(LC)-0.5。則阻抗矩陣Z為互易矩陣且對稱，通過分析Z11及Z21即可得到矩陣網(wǎng)絡(luò)的性質(zhì)

(11)

假設(shè)品質(zhì)因數(shù)Q遠大于1，通過方程(11)可發(fā)現(xiàn)當激勵源的頻率為如下值時

(12)

Re[Z11]達到極大值，Re[Z21]分別達到一個極大值和一個極小值(極小值為負)，且Im[Z11]和Im[Z21]為零，Z11與Z21的模同時也達到最大值。如圖10所示，此時端口阻抗出現(xiàn)頻率分叉現(xiàn)象。

圖10 端口阻抗隨頻率和耦合系數(shù)的變化

當耦合系數(shù)為1時，兩線圈達到緊密耦合，ω-為無窮大，端口阻抗只出現(xiàn)單峰ω+=ω0/20.5。但這種情況是基于圖9a模型化之后的結(jié)果，實際上當線圈距離較近時，線圈之間的電場耦合不可忽略，線圈間分布電容的存在將導(dǎo)致端口阻抗的變化更加復(fù)雜。

當耦合系數(shù)為0時，Z11由雙峰變?yōu)閱畏澹浞逯殿l率為單線圈固有的諧振頻率點，相當于沒有與另外的線圈發(fā)生耦合，同時Z21全頻域為0。

通過以上分析，可得到耦合線圈的端口阻抗與耦合系數(shù)k的關(guān)系。在仿真計算過程中，可根據(jù)端口阻抗，尋找阻抗雙峰的極值頻率點，在這里應(yīng)盡量選取ω+計算耦合系數(shù)，其原因是ω-高于諧振頻率點，尤其耦合系數(shù)較大時，ω-的阻抗特性較易與線圈下一個頻率點附近的阻抗相疊加，那么此時找到的阻抗峰值很有可能已經(jīng)受到更高頻時等效分布參數(shù)的影響。則根據(jù)式(13)反算的耦合系數(shù)為

(13)

值得注意的是，當端口阻抗由于線圈之間的耦合發(fā)生變化時，并不說明線圈本身的諧振頻率發(fā)生變化，傳輸系統(tǒng)的諧振頻率點仍應(yīng)選擇線圈的自諧振頻率點。

3.2 耦合系統(tǒng)實驗對比分析

以圖5中Ⅱ型線圈為例，建立雙線圈耦合系統(tǒng)，并進行仿真計算，其仿真過程與2.3節(jié)相似。同時通過實驗測量雙線圈之間的耦合系數(shù)。通過仿真得到的耦合線圈空間磁場分布如圖11所示，系統(tǒng)的端口阻抗如圖12所示，其計算得到的耦合系數(shù)與實驗對比如圖13所示。

可看出，通過有限元方法對于基于分布參數(shù)的無線電能傳輸系統(tǒng)的諧振線圈之間的耦合系數(shù)計算結(jié)果非常接近實際測量結(jié)果，說明通過HFSS結(jié)合端口阻抗特性計算耦合系數(shù)的方法可應(yīng)用于傳輸系統(tǒng)的設(shè)計中。

當獲得系統(tǒng)的耦合系數(shù)以及品質(zhì)因數(shù)后，實際上可根據(jù)耦合模理論或電路結(jié)構(gòu)計算無線電能傳輸系統(tǒng)的傳輸效率，這方面的研究已比較深入。通過仿真軟件雖然也能通過計算散射參數(shù)(S21)間接計算傳輸效率[20]，但其需要嚴格的阻抗匹配過程。這一過程需要考慮負載阻抗以及驅(qū)動源的端口阻抗，關(guān)于這方面的研究已比較完備。但此時系統(tǒng)的傳輸效率僅是端口的傳輸效率，忽略了電源內(nèi)部的損耗。另外，從圖11中可看到，當耦合線圈之間的距離發(fā)生變化時，端口阻抗同樣發(fā)生變化，那么就需要端口阻抗的自適應(yīng)匹配技術(shù)[11]。所以這種通過散射參數(shù)表征無線電能傳輸系統(tǒng)傳輸效率的方法尚需深入研究。

圖11 線圈耦合諧振時的磁場分布

圖12 耦合線圈端口阻抗仿真結(jié)果

圖13 仿真耦合系數(shù)與實驗對比

4 結(jié)論

針對磁耦合諧振式無線電能傳輸分布參數(shù)自諧振線圈參數(shù)提取的問題，建立在低頻段的等效集中參數(shù)模型，通過分析其端口阻抗特性，提出固有頻率及品質(zhì)因數(shù)的計算方法。進一步根據(jù)耦合線圈端口阻抗分裂特性提出耦合系數(shù)的計算方法。結(jié)合高頻有限元仿真軟件，利用建模仿真分析的方法提取了其關(guān)鍵特征參數(shù)。同時，結(jié)合人體植入式無線供電裝置中的實際線圈，實驗測量其分布參數(shù)，與仿真參數(shù)進行比對，驗證了計算方法的有效性。這種分布參數(shù)計算的方法可進一步應(yīng)用于分布參數(shù)無線電能傳輸系統(tǒng)的仿真設(shè)計中，為實際傳輸平臺的搭建提供了參數(shù)參考。

[1] Kurs A，Aristeidis K，Robert M，et al.Wireless power transfer via strongly coupled magnetic resonances[J].Science，2007，317(5834)：83-86.

[2] Ahn D，Hong S.A transmitter or a receiver consisting of two strongly coupled resonators for enhanced resonant coupling in wireless power transfer[J].IEEE Transactions on Industrial Electronics，2014，61(3)：1193-203.

[3] Meyer P，Germano P，Markovic M，et al.Design of a contactless energy-transfer system for desktop peripherals[J].IEEE Transactions on Industry Applications，2011，47(4)：1643-1651.

[4] Matsumoto H，Daisuke T，Kouichi I，et al.Trifoliate three-phase contactless power transformer in case of winding-alignment[J].IEEE Transactions on Industrial Electronics[J]，2014，61(1)：53-62.

[5] Jaegue S，Shin S，Kim Y，et al.Design and implementation of shaped magnetic-resonance-based wireless power transfer system for roadway-powered moving electric vehicles[J].IEEE Transactions on Industrial Electronics，2014.61(3)：1179-92.

[6] Lee S，Choi B，Rim C T.Dynamics characterization of the inductive power transfer system for online electric vehicles by laplace phasor transform[J].IEEE Transactions on Power Electronics，2013，28(12)：5902-5909.

[7] Budhia M，Boys J T，Covic G A，et al.Development of a single-sided flux magnetic coupler for electric vehicle ipt charging systems[J].IEEE Transactions on Industrial Electronics，2013，60(1)：318-328.

[8] Kuipers J，Bruning H，Yntema D，et al.Self-capacitance and resistive losses of saline-water-filled inductors[J].IEEE Transactions on Industrial Electronics，2014，61(5)：2356-2361.

[9] Kiani M，Jow U M，Ghovanloo M.Design and optimization of a 3-coil inductive link for efficient wireless power transmission[J].IEEE Transactions on Biomedical Circuits and Systems，2011，5(6)：579-591.

[10]Duong T P，Lee J W.Experimental results of high-efficiency resonant coupling wireless power transfer using a variable coupling method[J].IEEE Microwave and Wireless Components Letters，2011，21(8)：442-444.

[11]Park J，Tak Y，Kim Y，et al.Investigation of adaptive matching methods for near-field wireless power transfer[J].IEEE Transactions on Antennas and Propagation，2011，59(5)：1769-1773.

[12]Sample A P，Meyer D A，Smith J R.Analysis，experimental results，and range adaptation of magnetically coupled resonators for wireless power transfer[J].IEEE Transactions on Industrial Electronics，2011，58(2)：544-554.

[13]Wang H，Mao Z H，Xu Q，et al.Relay effect on wireless power transfer using resonant coupling[C].38th Annual Northeast Bioengineering Conference，Philadelphia，PA，2012：428-429.

[14]RamRakhyani A K，Mirabbasi S，Mu C.Design and optimization of resonance-based efficient wireless power delivery systems for biomedical implants[J].IEEE Transactions on Biomedical Circuits and Systems，2011，5(1)：48-63.

[15]Xu Q，Gao Z，He J，et al.A novel mat-based system for position-varying wireless power transfer to biomedical implants[J].IEEE Transactions on Magnetics，2013，49(8)：4774-4779.

[16]Johari R，Krogmeier J V，Love D J.Analysis and practical considerations in implementing multiple transmitters for wireless power transfer via coupled magnetic resonance[J].IEEE Transactions on Industrial Electronics，2014，61(4)：1774-1783.

[17]Choi B，Nho J，Cha H，et al.Design and implementation of low-profile contactless battery charger using planar printed circuit board windings as energy transfer device[J].IEEE Transactions on Industrial Electronics，2004，51(1)：140-147.

[18]Haus H A.Waves and Fields in Optoelectronics[M].Prentice Hall，Englewood Cliffs，NJ，1984.

[19]李明洋.HFSS電磁仿真設(shè)計應(yīng)用詳解[M].北京：人民郵電出版社，2010.

[20]Chen Q，Ho S L，F(xiàn)u W N.A new low radiation wireless transmission system in mobile phone application based on magnetic resonant coupling[J].IEEE Transactions on Magnetics，2013，49(7)：3476-3479.

Characteristic Parameter Simulation Method for Magnetic Coupling Resonance Wireless Power Transfer Based on Port Impedance

MaoShitong1ZhuChunbo1SongKai1WeiGuo1ChiHaokun2

(1.Harbin Institute of Technology School of Electrical Engineering and Automation Harbin 150001 China 2.Ocean University of China College of Information Science and Engineering Qingdao 266000 China)

Abstract Utilizing high frequency finite element simulation software and combining with the characteristics of wireless power transfer (WPT) technique，the key parameters extraction and the simulation method are proposed in this paper，based on port impedance analysis for the single self-resonance coil and two-port network equivalent model for coupled coils respectively.The practical coil is measured as a reference to verify the simulation result.Moreover，the impedance split characteristic has been studied in order to propose the calculation method for the coupling factor.Such work can provide the ideas of the coil design used in WPT system.

Wireless power transfer，magnetic coupling resonance，high frequency finite element method，parameter extraction

國家自然科學基金重點項目(51277037)資助。

2015-06-03 改稿日期2015-08-02

TM724

毛世通 男，1985年生，博士研究生，研究方向為無線電能傳輸。

朱春波 男，1964年生，教授，博士生導(dǎo)師，研究方向為儲能系統(tǒng)綜合測試與控制技術(shù)，無線能量傳輸技術(shù)。(通信作者)