基于傳感器丟包率不確定性預測的分布式H∞濾波算法*

林 楠，史葦杭，魏 斌

(1.鄭州大學 軟件技術學院，河南 鄭州450002;2.鄭州大學 計算機科學與技術學院，河南 鄭州450002)

0 引 言

近年來，越來越多的科學家對傳感器網絡的分布式濾波問題進行了研究［1，2］。分布式濾波中，傳感器通過拓撲網絡連接，且可以接收其自身感測的數據并通過互聯網傳輸信息。因此，如何處理傳感器之間的復雜耦合關系成為設計分布式濾波器的最重要的問題之一［3，4］。H∞濾波方法與其它濾波器相比提供了一個最壞情況下的估計誤差界限，并且不需要噪聲統計知識，因此，被廣泛地應用到實際工程中，并成為控制領域的一個研究熱點。

傳感器網絡的通信介質的可靠性受到外部環境的影響，并且數據包丟失在期望上的統計量很難獲取［5，6］。因此，需要在傳感器網絡分布式估計中對數據包丟失的不確定性進行分析，無論是本地傳感器還是相鄰傳感器的數據包丟失。

在分布式H∞濾波的研究上，吳博等人［7］通過使用穩態Kalman 濾波器對多個傳感器節點的輸出信號進行濾波，提出一種帶濾波的無線傳感器網絡(WSNs)的H∞控制算法。馮肖亮等人［8］利用測量值擴維的方法，提出基于多傳感器的序貫式融合有限域H∞濾波方法。李秀英等人［9］通過定義新的變量，將原系統轉化為隨機參數系統，提出一種具有一步隨機時滯和多丟包的網絡系統H∞濾波器設計方法。Dong Hongli 等人［10］提出一種有損傳感器網絡Markov跳躍非線性時滯系統的分布式H∞濾波器。Jiang Bin 等人［11］通過分析與設計全階H∞濾波器，提出基于網絡控制系統的T-S 模糊模型法的濾波器設計方案。

1 問題建模

采用Hn來表示n 維的歐氏空間，用Hn×k來表示所有n×k矩陣的集合。用x 表示隨機向量，用‖x‖表示向量x的歐幾里得范數，用I 表示單位矩陣［12，3］。E(x)，E(x|y)分別為隨機變量x 的期望和在條件y 下x 的期望。

x(t)為狀態向量，z(t)為被估計的信號，線性離散時間系統的表達如下

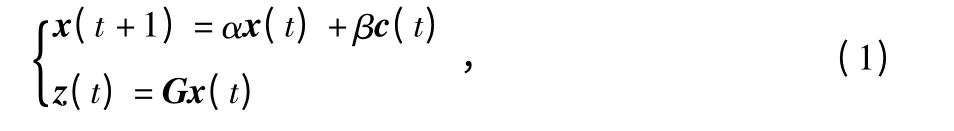
式中 c(t)為外界干擾輸入，而m 只傳感器服從隨機數據包丟失的情況如下

式中 ys(t)為通過傳感器s 接收到的來自線性離散時間系統的測量輸出。As(t)為伯努利分布隨機變量。

假設有N 個傳感器節點分布在空間并通過一個固定的拓撲結構的無線網絡進行連接。傳感器網絡通過一個有向圖G={V，E}進行表示，V=(v1，…，vN)表示傳感器網絡節點集合，E=(e1，…，em)表示鏈路集合。來自節點vj的信息有以下基于狀態跟蹤的形式來接收隨機丟包

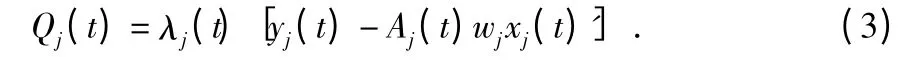
其中，xj(t)'為在傳感器vj的xj(t)估算值。λj(t)為Aj(t)伯努利分布的獨立隨機變量，它代表著傳感器之間的分組傳輸。

代入式(2)～式(3)中得到

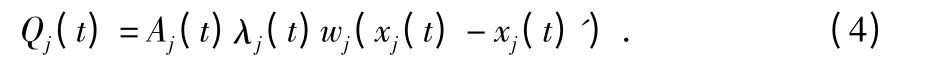
為了使分析更加方便，引入另一個符合伯努利分布的隨機參數Si(t)，定義

可以結合這兩個獨立的進程為一個，得到

根據實際環境的復雜性，討論不確定預期的丟包率。如果Sj(t)=1，則Ai(t)=λi(t)=1。可以得到

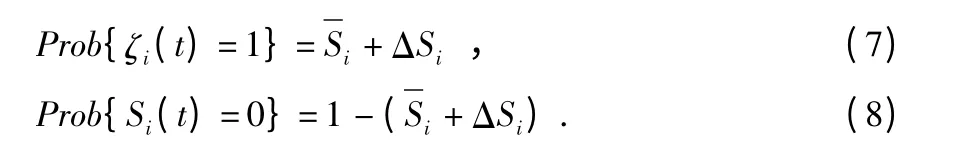
Si(t)的數學期望可以被描述如下

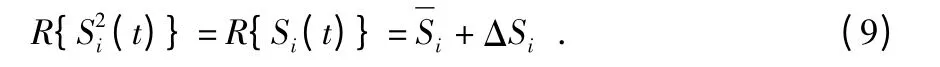
本文中，假設R{Si(t)}的不確定性是范數有界的，0≤|Si|≤γi≤1，定義，得到

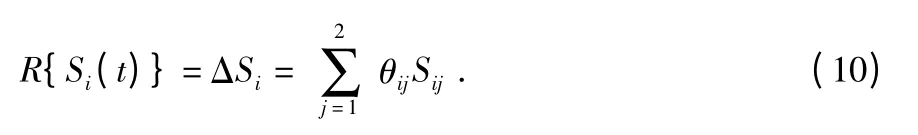
因此，通過傳感器i 所接收到的信息可以用線性離散時間系統表示為

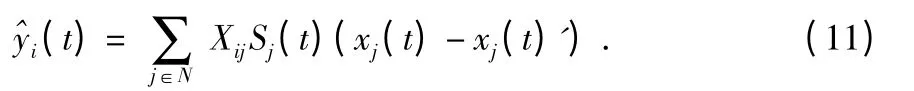
接著，在傳感器i 上采用濾波器

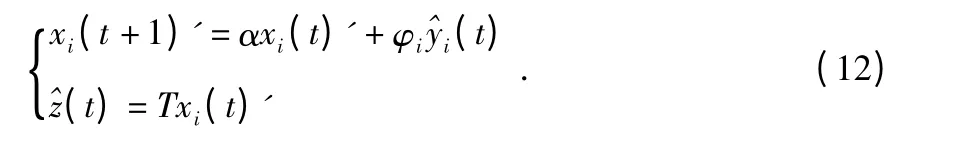
濾波器的初始值是xi(0)'=0，i=1，2，…，N。

將式(8)代入式(9)可得

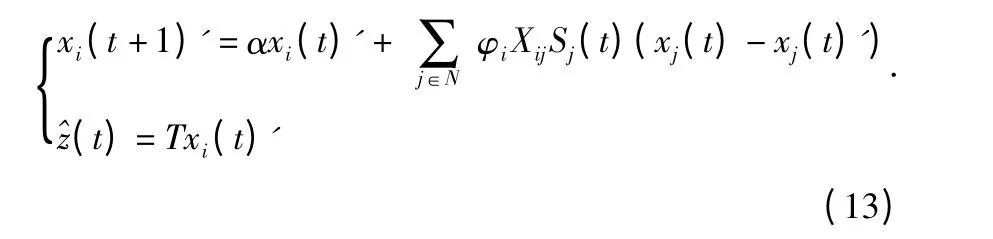
令估計誤差和濾波誤差分別為

對于節點i 可以得到管理濾波誤差的線性離散時間系統

2 分布式H∞濾波

在本節中，在均方意義上對于離散時間系統的隨機穩定性問題，采用一個丟包的不確定數學期望來進行討論。通過采用參數依賴Lyapunov 泛函的方法和隨機分析技術來獲取可驗證性條件，最終目的是找到最佳的濾波器參數φi。

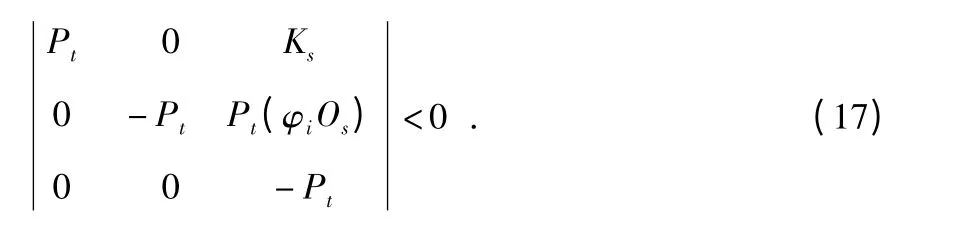
其中

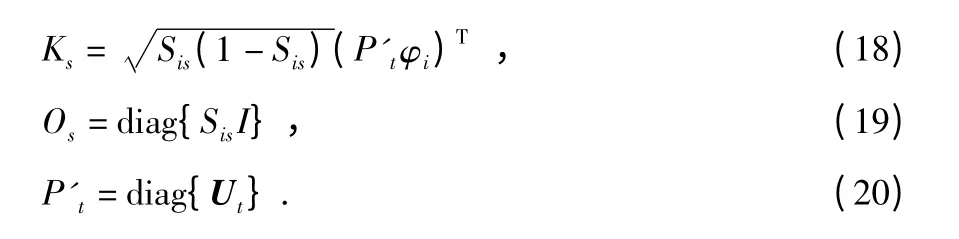
最后可以得到濾波器參數φi為

3 算例分析

假設有一個線性離散時間系統，如下所示

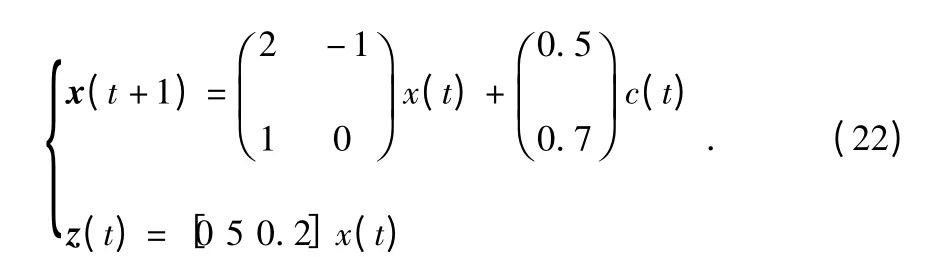
傳感器網絡的拓撲結構通過一個節點集合為V=(1，2，3)，鏈路集合為E={(1，1)，(1，2)，(2，2)，(2，3)，(3，3)}的有向圖G={V，E，L}表示，鄰接矩陣L 表示為

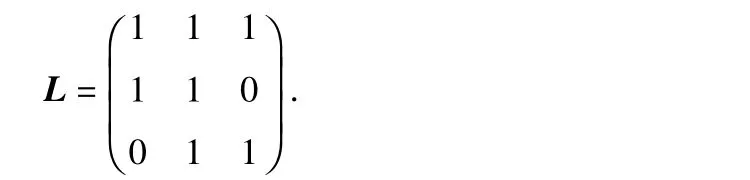
傳感器節點的動態性用參數描述為w1=［0，－0.2］，w1=［0.1，－0.2］，w1=［0.2，0.4］。

表1 對于不同的Si 況下γi 和φi 取值Tab 1 Value of γi and φi with different

表1 對于不同的Si 況下γi 和φi 取值Tab 1 Value of γi and φi with different

圖1 給出了在相同情況下，通過200 次Monte—Carlo 測試本文濾波器和文獻［10］的Markov 跳躍非線性時滯系統的分布式H∞濾波器、文獻［11］的T-S 模糊模型法的濾波器的比較結果。

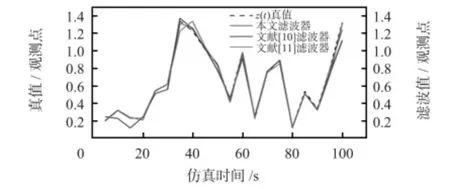
圖1 真值與濾波值的對比情況Fig 1 Comparison of true value and filtering value

從圖1 的對比結果可以看出:本文所提出的估計算法的濾波精度高于文獻［10，11］的濾波算法，其中，文獻［10］的濾波算法與真值的偏差較大，而本文算法的濾波曲線貼近于真值的曲線。由此可見，在網絡環境下，即當觀測數據存在不確定性丟包時，本文濾波算法更加有效。

對濾波器進行了100 次的蒙特—卡羅仿真，得到了估計值與實際值之間的誤差。如圖2 所示，隨著仿真步數的增長，三種濾波器的誤差值呈現不穩定的變化，本文濾波器的誤差在(0.005 4，0.015 4)包之間，文獻［10］濾波器在(0.007 8，0.017 2)包之間，文獻［11］濾波器的誤差在(0.009 4，0.018 9)包之間。由于信號干擾導致測量值的丟失，估算值與實際值往往存在著偏差，本文正是基于測量數據不確定丟失的問題進行了建模，并通過最佳的濾波器參數來減少估算誤差。從數值上可以看出:本文濾波器的絕對誤差估計比另外兩種濾波器更加有效。

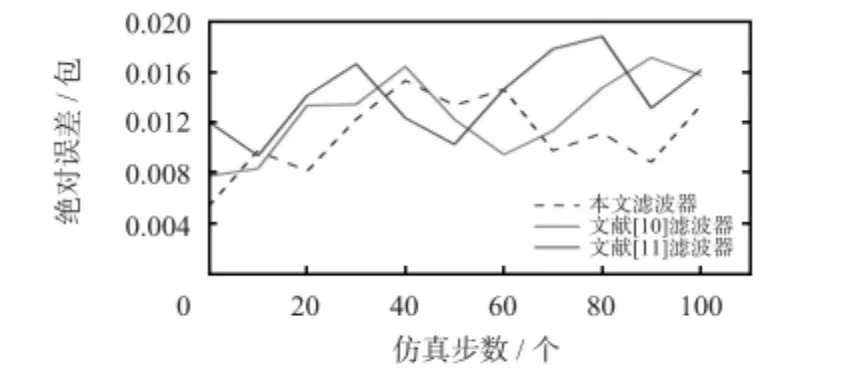
圖2 絕對誤差估計Fig 2 Absolute error estimation

為了進一步地分析網絡不確定性因素對濾波誤差動態系統穩定性的影響。在圖2 的基礎上，增加了網絡延時、數據丟包因素，設置網絡每發送一次數據延遲0.05 ms，數據丟包率為7.3%，在這種網絡狀態下算法濾波的誤差值。從圖3 中的結果可以看出:本文算法的濾波誤差值的變化范圍在(0.006 1，0.016 2)包之間，相比圖2 中的情況，受到網絡狀態變化后的誤差值有少許增加。文獻［10］的變化范圍為(0.009 2，0.018 4)包，受到網絡狀態影響時誤差值的變化最大。文獻［11］的變化范圍為(0.010 5，0.018 6)，在網絡狀態剛發生變化時，誤差值增大，之后最大的誤差值不超過之前的0.018 9，但從曲線的總體分布情況來看仍高于本文提出的分布式H∞濾波算法。

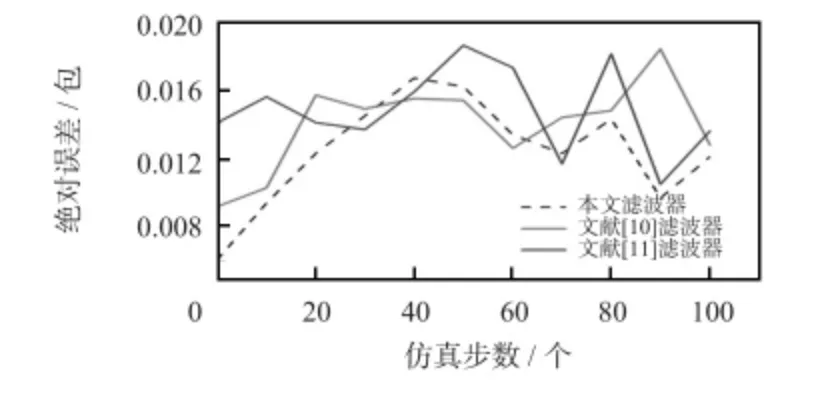
圖3 在其他網絡狀態下的絕對誤差Fig 3 Absolute error value in other network status

4 結 論

本文提出一種基于傳感器丟包率不確定性預測的分布式H∞濾波算法，通過管理濾波誤差的線性離散時間系統，在均方意義上對于離散時間系統的隨機穩定性問題進行了討論，并且采用參數依賴Lyapunov 泛函的方法和隨機分析技術來獲取可驗證性條件，通過找到最佳的濾波器參數來最終實現H∞濾波的穩定性和精確性。在實驗中通過與Markov跳躍非線性時滯系統的分布式H∞濾波器和T-S 模糊模型法的濾波器進行對比，體現出本文濾波算法的有效性。

［1］ Qin F，Dai X，Mitchell J E.Effective-SNR estimation for wireless sensor networks using Kalman filter［J］.Ad Hoc Networks，2013，11(3):944－958.

［2］ Demigha O，Hidouci W K，Ahmed T.On energy efficiency in collaborative target tracking in wireless sensor networks:A review［J］.Communications Surveys ＆ Tutorials，IEEE，2013，15(3):1210－1222.

［3］ Solouk V，Taghizadeh H，Akbari-Moghanjoughi A，et al.Tracking moving targets in wireless sensor networks using extended diffusion strategies of distributed Kalman filter［C］∥2013 IEEE Malaysia International Conference on Communications(MICC)，IEEE，2013:213－216.

［4］ Benini A，Mancini A，Longhi S.An IMU/UWB/vision-based extended kalman filter for Mini-UAV localization in indoor environment using 802.15.4a wireless sensor networks［J］.Journal of Intelligent＆Robotic Systems，2013，70(1－4):461－476.

［5］ Weeraddana D M，Walgama K S，Kulasekere E C.Dempster-Shafer information filtering in multi-modality wireless sensor networks［J］.World Academy of Science，Engineering and Technology，2013，79:644－651.

［6］ Torfs T，Sterken T，Brebels S，et al.Low power wireless sensor networks for building monitoring［J］.Sensors Journal，IEEE，2013，13(3):909－915.

［7］ 吳 博，關治洪，詹習生.帶濾波的無線傳感器網絡的H1 控制［J］.控制理論與應用，2013，30(2):261－265.

［8］ 馮肖亮，文成林，劉偉峰，等.基于多傳感器的序貫式融合有限域H∞濾波方法［J］.自動化學報，2013，39(9):1524－1532.

［9］ 李秀英，王金玉，孫書利.具有一步隨機時滯和多丟包的網絡系統H∞濾波器設計［J］.自動化學報，2014，40(1):155－160.

［10］Dong H，Wang Z，Gao H.Distributed H∞filtering for a class of Markovian jump nonlinear time-delay systems over lossy sensor networks［J］.IEEE Transactions on Industrial Electronics，2013，60(10):4665－4672.

［11］Jiang B，Mao Z，Shi P.Filter design for a class of networked control systems via T-S fuzzy-model approach［J］.IEEE Transactions on Fuzzy Systems，2010，18(1):201－208.

［12］Ma J，Sun S L.Information fusion estimators for systems with multiple sensors of different packet dropout rates［J］.In formation Fusion，2011，12(3):213－222.

［13］Sun Y G，Qin S Y.Stability and stabilization of networked control systems with bounded packet dropout［J］.Acta Auto matica Sinica，2011，37(1):113－118.

［14］Gao H，Li Z，Agarwal R.New result on H∞filtering for time-delay Markovian jump systems［C］∥2013 IEEE International Symposium on Industrial Electronics(ISIE)，IEEE，2013:1－6.