GPS高程擬合方法的研究和應用

王 珍，程 壘

(1．北京市勘察設計研究院有限公司，北京100038;2．中科遙感科技集團有限公司，北京100080)

一、引 言

對于線路長、高差大等地形情況復雜的工程，要完成地形圖測量任務，無論是采用常規的地形圖測量方法還是航空攝影測量技術，都需要在先完成首級平面和高程控制網測量的基礎上，完成次級的具有平面坐標和高程的圖根控制點測量。

常規的導線測量和水準測量的方式，外業測量和內業平差都耗時長且容易出錯。GPS全球定位系統具有測量快、布網靈活、平面精度高等優點，但高程控制網卻相對較弱一些。同時，GPS測定的高程是大地高，是地面點沿法線方向到參考橢球面的距離;而常見的工程采用的高程系統為正常高高程系統，正常高是地面點沿鉛垂線至似大地水準面的距離，通過水準測量確定。如何將GPS測得的大地高轉換為正常高，是線路長且面積較大項目的難點之一。如圖1所示。

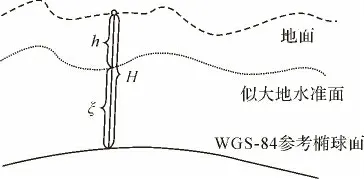
圖1 某點大地高與正常高的示意圖

二、GPS高程擬合的原理

GPS高程擬合的原理是利用既有GPS大地高H又有正常高的Hr的多個已知點，按式(1)求出這些公共點的高程異常值ξ。然后由公共點的平面坐標和ξ值，采用數學擬合的方法，擬合出測區內的似大地水準面。再根據其他GPS點的平面坐標擬合出各點的高程異常ξi，則按式(2)可求得GPS網中各點的正常高Hr

三、GPS高程擬合的方法

GPS高程擬合方法有函數模型、統計模型、組合模型、重力模型等方法。而目前最常用的方法是多項式擬合方法。

1．二次多項式擬合法［1］

多項式函數擬合法的基本原理是:在區域GPS網內，將似大地水準面看成曲面或平面，將高程異常ξ表示為平面坐標(x，y)或大地坐標(B，L)的函數，通過既有GPS觀測又有水準資料上點的高程異常確定測區內似大地水準面的模型或形狀，從而得到其他點上的高程異常，其數學模型為

式中，f(x，y)是擬合的似大地水準面模型;ε是擬合誤差。

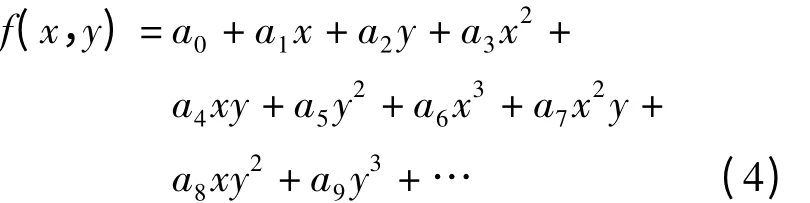
式中，a0，a1，a3，…，an為擬合待定參數;x、y為各GPS點的平面坐標，坐標x、y可改為經緯度B、L。合并式(3)、式(4)后便可得二次多項式曲面擬合模型

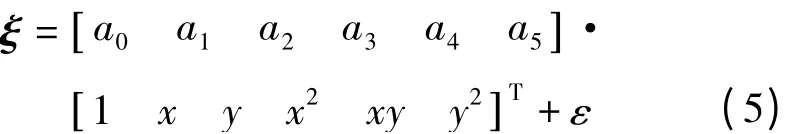
多項式擬合模型為

式中，

根據最小二乘原理(ε2=min)求得擬合系數，得到

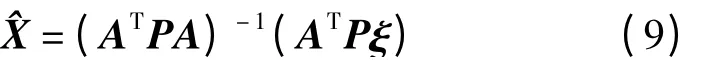
對于二次和三次多項式，則至少分別需要6個和10個以上已知點來確定模型中的參數。

2．雙線性多項式內插法［2］

雙線性多項式內插法的數學模型為

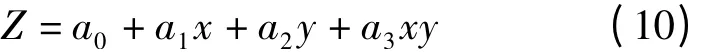
式中，x、y為平面坐標;Z為高程;a0、a1、a3為擬合待定參數。

四、GPS的精度評定

為了客觀地評定GPS高程轉換的精度，在布設幾何水準聯測點時，應適當多聯測幾個GPS點，其點位也應均勻分布，作為外部檢核。

1．內符合精度

根據參與擬合計算已知點的高程異常ξi與擬合值ξ'i，用vi=ξ'i－ξi求擬合殘差vi，按式(1)計算GPS高程擬合計算的內符合精度μ

式中，v為擬合(檢核)殘差;N為參與計算的點個數;T為必要觀測數。

2．外符合精度

根據檢核點值ξ'i與擬合值ξi之差，按下式計算GPS水準的外符合精度M

式中，n為檢核點數。

五、具體實例

Matlab集數值分析、矩陣運算和圖形為一體，可方便應用于數據分析和工程繪圖。本文采用Matlab環境中的二次多項式擬合法和雙線性多項式內插法進行運算。樣例數據為某平原地區100點(選擇50點擬合點，50點檢核點)及山地地區30點(23點擬合點，7點檢核點)，分別進行上述兩種擬合方式。部分數據見表1。

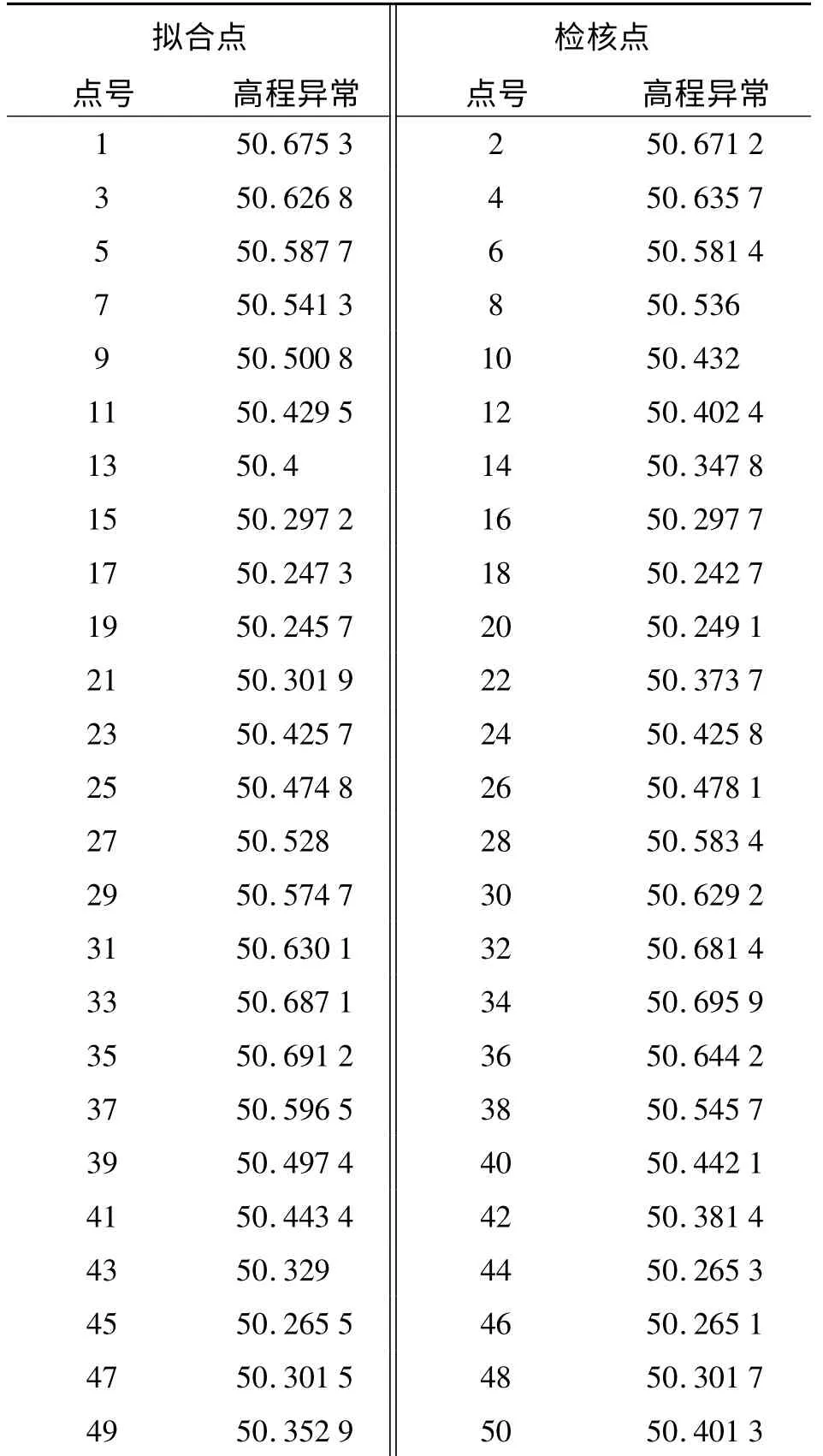
表1 平原地區高程異常

圖2 平原區采用雙線性擬合殘差圖

從圖2—圖5及表2中可以看出，二次多項式擬合法不適合平原地區擬合，最大高程異常的絕對值竟達1．903 m。而雙線性擬合法精度比較適應于平原地區，高程擬合精度較優。

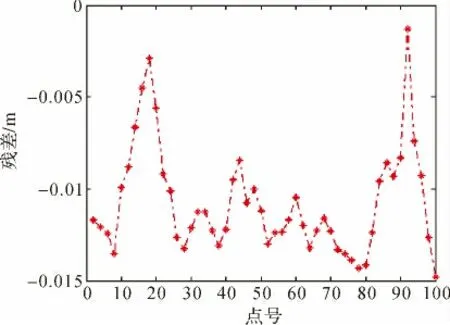
圖3 平原區采用雙線性擬合檢核殘差圖

圖4 平原區采用二次多項式擬合殘差圖

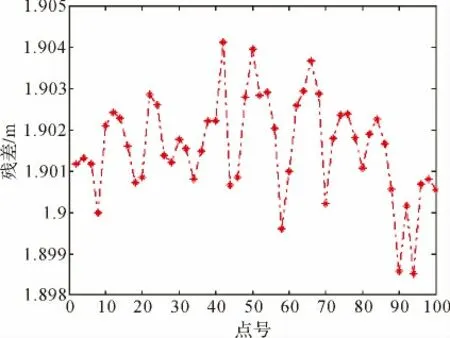
圖5 平原區采用二次多項式檢核殘差圖

表2 二次多項式擬合與雙線性擬合法的對比(平原地區)m

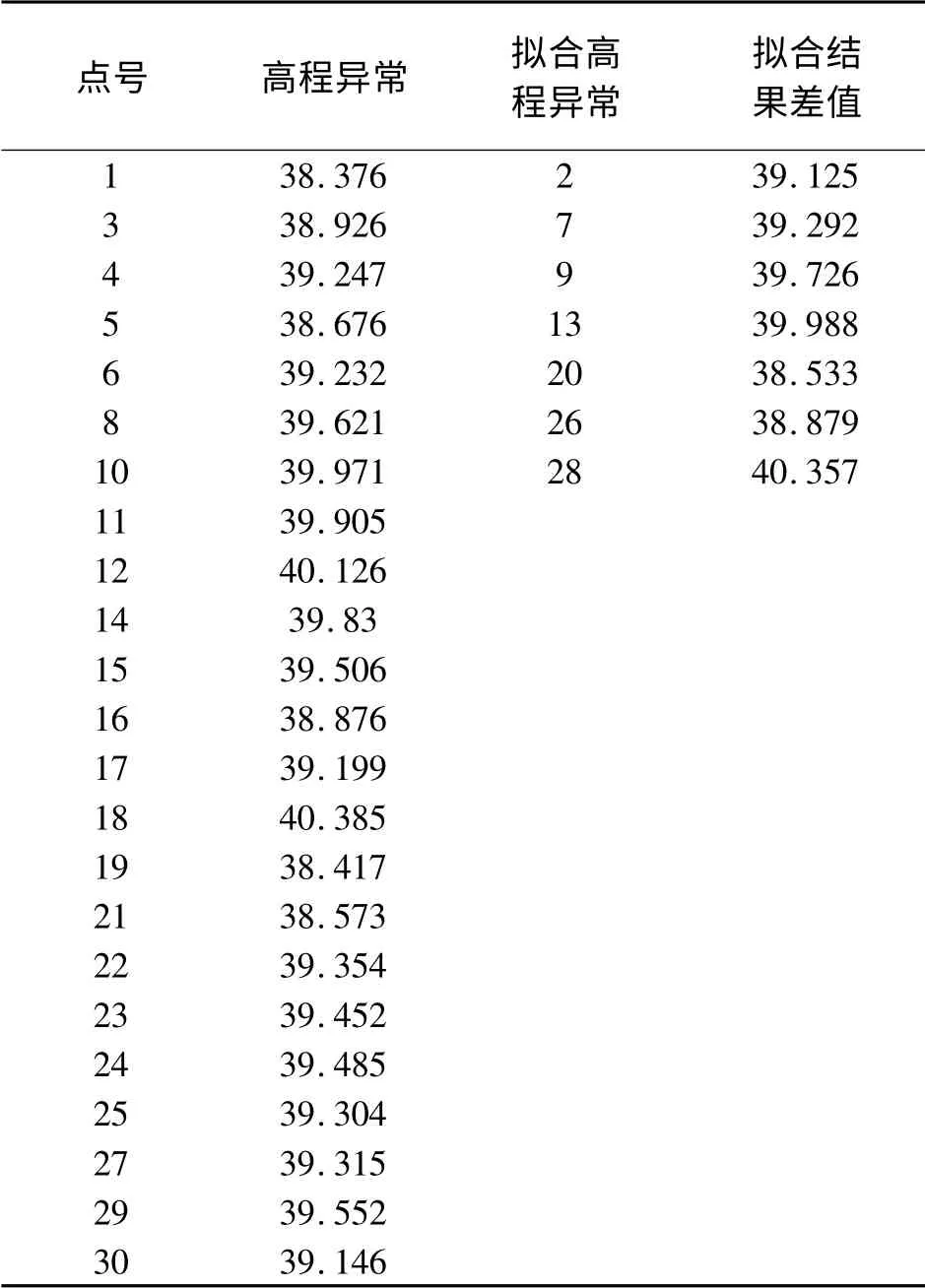
表3 山區的高程異常 m

從圖6—圖9及表4中可以看出，與二次多項式擬合法相比，雙線性擬合法不適合山區的高程擬合。二次多項式擬合法精度較好。

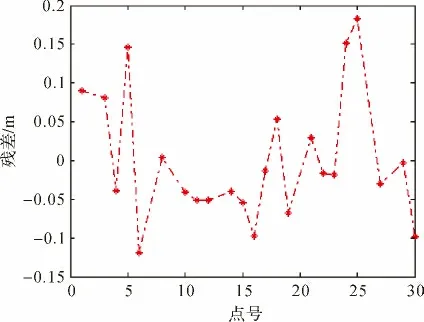
圖6 山區雙線性擬合殘差圖

表4 二次多項式擬合與雙線性擬合法的對比(山區)m

圖7 山區雙線性擬合檢核殘差圖

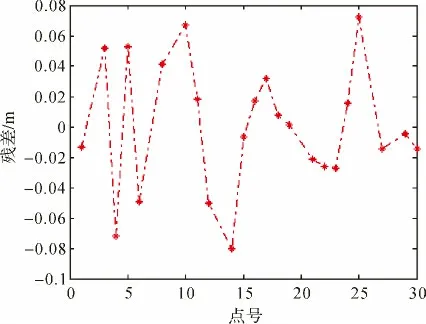
圖8 山區二次多項式擬合殘差圖

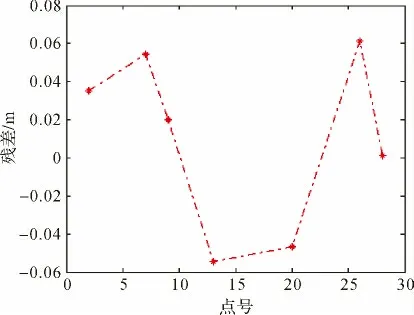
圖9 山區二次多項式檢核殘差圖

從表5中可以看出，雙線性擬合法能夠滿足平原地區的高程擬合精度，二次多項式能夠滿足山區的高程擬合精度，且能達到圖根測量精度。

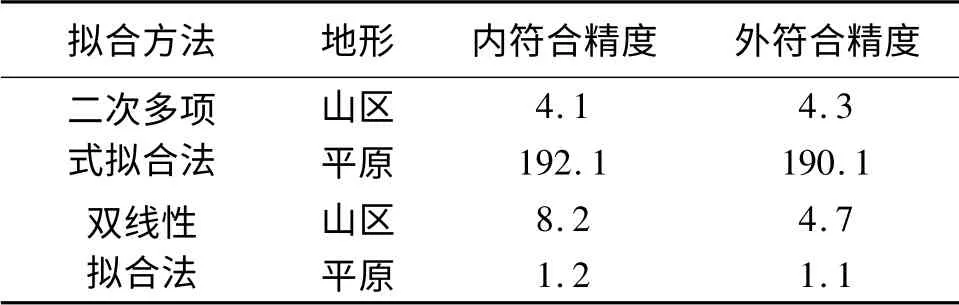
表5 二次多項式擬合法與雙線性擬合法精度比較cm

六、結束語

通過Matlab能夠快速實現GPS高程與水準高程的轉換，該方法可以降低外業工作量，同時滿足了高程精度測量的要求。在目前所內進行的興延路項目中也利用了該方法進行高程加密測量工作。上述擬合方法的數據驗證為類似工程的高程擬合提供了借鑒。

另外，在實際工程應用中，應結合現場的情況靈活運用二次多項式擬合法和雙線性擬合法進行高程擬合。同時，為提高GPS高程擬合的精度，除了選用最優的擬合方法外，還應保證擬合點間高程異常的精度，提高水準高和大地高的精度。

［1］ 黃征凱．確定區域似大地水準面方法的比較分析［D］．桂林:桂林理工大學，2013．

［2］ 張紅華，孫月問．GPS高程擬合方法及精度分析［J］．測繪與空間地理信息，2014(2):132-138．