標尺傾斜時精密水準測量方法研究
陳 波,李 航,綦曉杰,朱瑞琪,李玉寶
(東南大學交通學院,江蘇 南京211189)
一、引 言
在工程測量和變形監測的過程中,經常因工地上施工材料、渣土堆積、腳手架安裝、施工機械設置等各種因素致使埋設的監測目標點點位被部分遮擋或覆蓋。影響到儀器或標尺在點位上的正常整置和觀測,使得測量工作不能順利地進行和延續。為了使變形監測工作不間斷地延續下去,一般是采取移動點位、重新設置監測點等方法,但這樣會因點位移動需要重新測量初始值,使得監測工作不連貫,影響監測對象整體性的正確判斷和分析,同時也帶來一定經濟損失。
當采用水準測量進行沉降變形監測時,若由于前述的原因,不能正常整置標尺,可將標尺前后或左右傾斜放置到監測點位上。本文對這種非正常放置標尺的情況,通過在傾斜標尺上讀數以及距離偏離值等數據的采集,從而間接地計算出“高差偏心改正”,經改正后的讀數相當于在正常整置標尺時的正常讀數,并進行測量方法和精度,以及在球形監測標志上因傾斜整置標尺而對高差產生的高差偏心改正的分析和研究。
二、傾斜水準標尺觀測值采集
如圖1所示為標尺相對于儀器的視線方向前后傾斜的情況。在這種情況下由于障礙物的原因,在標志點位上無法正常地整置水準標尺,只能是使標尺傾斜,屬于標尺的非正常整置情況。若排除障礙后再測量,在當時還有一定的困難。變形監測的周期是有時間限制的,監測的時機不能耽誤。鑒于該種情況,如何在非正常整置標尺的情況下獲得觀測值、再通過一些必要的計算間接地獲取相當于在正常的情況下的正常觀測值,則需要進行探討和研究。
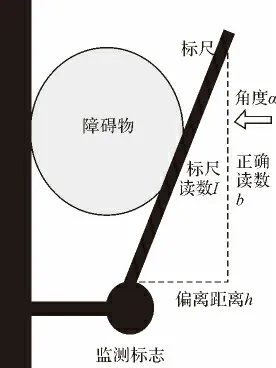
圖1 傾斜標尺示意圖(觀測方向從右至左)
如圖1中水準儀的傾斜觀測值為l,另外還要觀測輔助的參數——距離偏離值h或標尺傾斜角α(用鉛垂線配合小鋼尺解決h的測量;用掛傾斜儀和標尺側面的中軸的標志線量取α;依據觀測讀數和偏離距離計算α)。實際應用中因使用方便和更具有可操作性,測量距離偏離值h的情況較多。在這種情況下

三、水準測量數據處理方法
在標尺傾斜非正常整置標尺的情況下獲得的觀測值,通過一些必要數據處理工作,可間接地獲取相當于在正常情況下的觀測值。這里需要進行兩方面的工作,一是數據處理,獲取等價的觀測值;二是進行必要的精度分析。
1.間接計算的正常讀數和精度分析
如圖1所示,當獲取了l、h后,可按下式間接計算相當于正確的標尺讀數b

現在的問題是間接計算的數值b的精度是否能達到一定相應的要求。于是對式(2)進行全微分
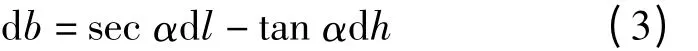
由誤差傳播定律得

設式(4)中右端的第一項的平方根為

右端的第2項的平方根為

現行規范要求二級變形監測,測站高差的中誤差為±0.5 mm。因實際高差計算是通過基本分劃和輔助分劃讀數計算,取高差平均值h站作為測站的測量結果,各讀數為同精度獨立觀測值、中誤差為m。結合誤差傳播定律,得到

綜合考慮式(4)—式(7),以及根據等影響原則,可判定式(5)、式(6)所表達的誤差無顯著的差異
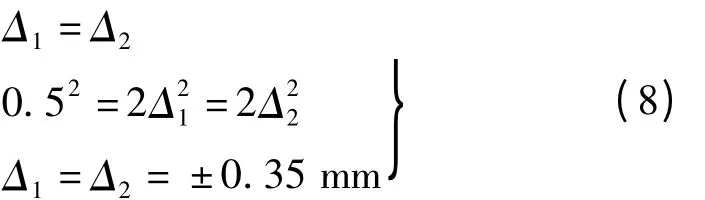
間接計算的正常標尺讀數b的誤差主要來自標尺的讀數誤差以及偏離距離的量測誤差,它們都以一定的傳播規律影響間接計算的標尺正常讀數b。
2.讀數誤差對間接正常讀數的影響
由(6)式,可分析Δ1、α、m1之間的關系和規律。由Δ1=±0.35 mm=m1secα計算分析數據可知:
當傾斜角度α為1°~9°時,在標尺傾斜情況水準儀在標尺上的讀數為l,讀數誤差對間接正常讀數的影響隨標尺傾斜程度的增加而增加,但增加的速度比較緩慢,影響并不顯著,在取位精度為0.001 mm的情況下,有Δ1=±0.35 mm=m1。
要保持Δ1數值精度不變,當傾斜角度α為10°~17°時,觀測精度在原來的基礎上需提高,即ml=±0.01 mm、ml=±0.02 mm的量級。如傾斜還要增大,則還需重新計算觀測讀數的精度需提高的量級并實施,才能保持Δ1數值精度不變。
另外指出,當標尺傾斜時,標尺與監測點標志的接觸點要以標尺底部中心處為準。
3.偏離距離誤差對間接正常讀數的影響
由式(6)分析Δ2、α、mh之間的關系和規律。由Δ2=±0.35 mm=mh·tanα計算分析數據可知:
在標尺傾斜的情況下,偏離距離h(圖1)的測量誤差對間接計算正常讀數的影響隨標尺傾斜程度的增加而增加、速度比較快;要保持Δ2數值精度不變,當傾斜角度α為1°、10°、17°時,h測量的精度要求在±20.05 mm、±1.98 mm和±1.14 mm。如傾斜還要增大,則還需重新計算觀測讀數的精度并付諸實施,量測的精度的要求將更加寬松。所以量測h時,只要采用一般檢驗合格的鋼卷尺就不難達到要求。
另外指出,當標尺傾斜時,標尺與監測點的接觸點要以標尺底部中心處為準。
4.高差改正
當監測標志為平頂形狀時(如圖2所示),測量計算的高差無高差偏心改正;但當監測標志為圓形時,在實際的工作中大多采用該球形的變形監測標志。在正常的觀測情況下,標志與標尺的接觸點在正上部,其接觸點為唯一的,且標尺厚度對觀測無影響。但當標尺為非正常整置,即傾斜的時候,標尺與標志的接觸點就發生了位移,偏離標志最高的部位,而總是比正常的標尺讀數偏大,而導致點的高程偏小。因此需加入因標尺傾斜而對測量產生的高差改正數。如圖2所示,為在球形監測標志上非正常整置標尺的情況,最后的正確標尺讀數還需要減去高差歸心改正數x、標尺厚度改正數y的修正。
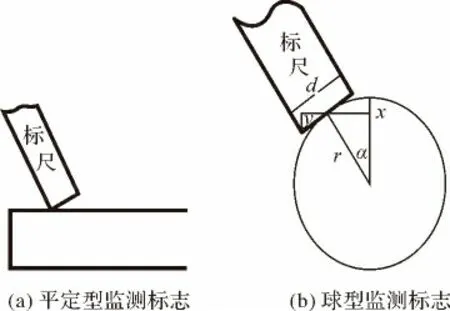
圖2 不同形狀標志偏心改正
根據圖1、圖2中所標出的符號尺寸不難得出其正確的間接計算標尺觀測值讀數b的數值為

式中,x為高差歸心改正數;y為標尺厚度改正數。設高差改正數δh=x+y,一般情況下標尺厚度較小,當標尺的傾斜角α較小、監測球形標志的半徑不是太大(一般r=5 mm,可用游標卡尺進行測量),當δh=≤m讀/3(m讀為讀數的中誤差)時,根據忽略不計原則,當高差改正數不大于m讀/3時,可無須考慮該項改正計算。按照這個思路,則有

考慮較為不利的情況,當r=5 mm、d=1 cm、m讀=0.5 mm、α=10°時,不符合上述條件。所以一般應根據測量球形標志的半徑、觀測的精度、高程成果的要求精度、標尺傾斜的程度等,考慮高差的偏心改正問題。當情況不滿足上述條件時,應按式(9)計算正常的間接正確標尺讀數,以保證所計算的高程成果的正確性和可靠性。
四、結束語
在地下工程及一些工地施工測量過程中,標尺傾斜是一個經常遇到的問題,本文對這個問題展開了較為詳盡的研究,開發了一個實用小程序運用于解決實際問題。
[1] 張正祿.工程測量學[M].武漢:武漢大學出版社,2005.
[2] 李玉寶.控制測量[M].北京:中國建筑工業出版社,2003.
[3] 中華人民共和國建設部.GB50026—93工程測量規范[S].北京:中國建筑工業出版社,1999.
[4] 武漢大學測繪學院測量平差學科組.誤差理論與測量平差基礎[M].武漢:武漢大學出版社,2014.

