基于次錨節點的無線傳感器網絡改進加權質心定位算法

張先超，劉興長，張春園

(后勤工程學院 后勤信息與軍事物流工程系，重慶401311)

0 引 言

無線傳感器網絡(wireless sensor networks，WSNs)是由隨機部署在目標區域內的數量巨大的離散傳感器節點組成，通過無線通信方式形成的一個多跳的自組織網絡系統［1］。節點的位置信息對無線傳感器網絡十分重要，是其支撐技術，并且具有廣泛的應用［2］。研究提高定位精度是當前無線傳感器網絡研究的熱點［3～7］。

無線傳感器網絡的定位技術可分為兩類:基于測距(range-based)的技術和無需測距(range-free)的技術［8］。到達時間差(time difference of arrival，TDOA)測距技術廣泛應用于無線傳感器網絡定位，在不考慮非視距(NLOS)誤差的情況下可取得較高的測距精度［9］。基于TDOA 測距的粒子群優化(PSO)無線傳感器網絡定位算法可比較準確地估計節點位置，但需要額外測距設備，增加了節點能耗。基于接收信號強度指示(RSSI)的加權質心算法通信開銷小，算法簡單［10］，但定位覆蓋率和定位精度受錨節點數目影響較大。

本文提出了一種基于次錨節點的改進加權質心定位算法(IWCLA-SAN)，以克服加權質心定位算法(WCLA)對錨節點數量要求較高和定位精度較低的缺陷。

1 粒子群優化定位算法

文獻［11，12］將粒子群優化算法應用于無線傳感器網絡定位中，驗證了該定位算法的可靠性。粒子群優化算法的實現原理如下:

假設在D 維的搜索空間內，存在一個種群大小為M 的粒子群，即無線傳感器網絡中的錨節點;存在一個數量為N的搜索目標群，即無線傳感器網絡中的未知節點。每個粒子在空間中的位置坐標xi=(xi1，xi2，…，xid)，搜索速度vi=(vi1，vi2，…，vid)，搜索到的個體最優位置為pi=(pi1，pi2，…，pid)，搜索到的全局最優位置為gb=(gb1，gb2，…，gbd)，其中，i=1，2，…，M，d=1，2，…，D。該算法采用下列公式對粒子操作

學習因子c1和c2是非負的常數，常設c1=c2=2;r1和r2是介于［0，1］的隨機數;w 為慣性權重，用來保持局部搜索和全局搜索的平衡，較大的w 有利于算法的全局搜索能力，較小的w 有利于算法的局部搜索能力;vid∈［-vmax，vmax］，vmax太大容易使粒子飛離最優解，vmax太小容易使粒子陷入局部最優，粒子的速度通常設為每維變換范圍的10%～20%;k 為當前迭代次數，T 為終止迭代次數;f 為適應度函數，di為未知節點到各錨節點的距離;錨節點的坐標Ai(xi，yi)，未知節點坐標Nj(xj，yj)，其中，i=1，2，…，M，j=1，2，…，N。

2 測距原理與質心定位算法

2.1 RSSI 測距原理

節點在通信時可以直接獲取RSSI 值，估計出未知節點與錨節點的距離。針對室外定位環境，文中采用自由空間傳播模型(free space propagation model)和對數—常態分布(log-normal distribution)模型，用于分析和仿真［13］。自由空間模型無線信道的數學模型如下

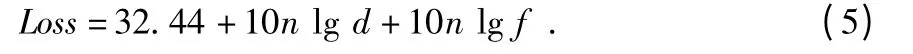
對數—常態分布模型無線信道的數學模型如下

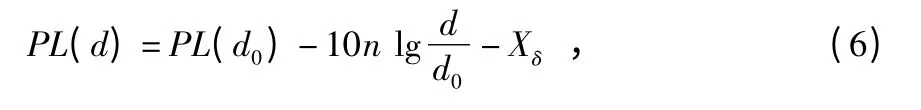
式中 PL(d0)為距離錨節點d0處的信號強度;PL(d)為距離錨節點d 處的信號強度;d 為未知節點與錨節點之間的距離;f 為頻率;d0為參考距離，一般取為1 m，將d=1 m 代入式(6)得到Loss，即PL(d0)的值;n 為信道衰減指數，一般取值2～4;Xδ為均值為零、方差δ 的高斯隨機噪聲變量。

通常情況下，測距誤差隨著測量距離的增加而增大［14］，即較大的RSSI 值計算得到的距離值誤差較小，而較小的RSSI 值計算得到的距離值誤差較大。

2.2 質心定位算法

圖1 CLA 示意圖Fig 1 Schematic diagram of centroid localization algorithm

2.3 WCLA

WCLA 通過對不同的錨節點賦予不同權值，達到了提高定位精度的目的。通常加權值是未知節點到錨節點距離的函數［15］，一般將未知節點與錨節點距離的倒數作為加權值，得到加權質心定位算法，其計算公式為

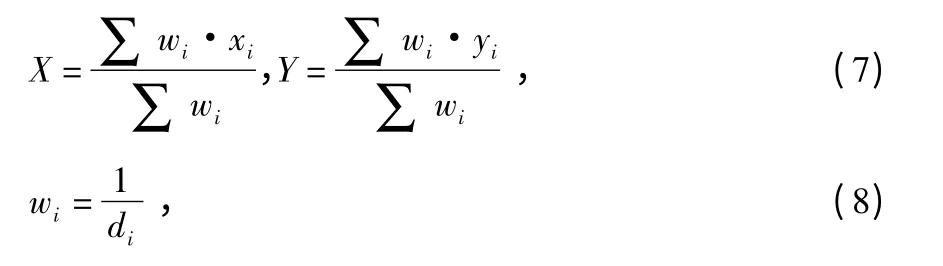
式中 (xi，yi)為錨節點的坐標，wi為加權因子，di為未知節點到錨節點的距離，i=1，2，…，n。

2.4 IWCLA

為了更加體現未知節點到通信范圍各錨節點距離對定位精度的影響，提出一種修正系數不固定的IWCLA。該算法對加權因子進行改進，設其為

其中，k 為修正系數，設定為

其中，D 為未知節點到通信范圍內錨節點距離集合元素方差的歸一化值，D 值的大小反映了未知節點通信范圍內各錨節點分布的均勻程度，分布越均勻D 值越小。根據D 值的不同設定k 的值，使得計算不同未知節點的坐標時，修正系數k 的值不同。如圖2 所示，對于錨節點分布均勻程度不同的兩種情況，圖2(a)的k 值大于圖2(b)的。本文根據通信范圍內各錨節點分布的均勻程度設定k 值，這樣更能增加距離未知節點較近的錨節點的權重，減少距離較遠的錨節點的權重。因此，與WCLA 相比，定位精度進一步提高。

2.5 IWCLA 描述

IWCLA 的定位步驟如下:

1)錨節點周期性發送自身節點ID 和自身節點位置信息，與鄰居節點進行通信。

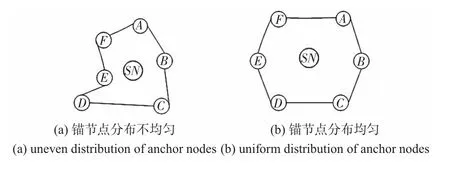
圖2 錨節點分布圖Fig 2 Diagram of anchor nodes distribution

2)未知節點收到錨節點信息后，分別記錄同一個錨節點的RSSI 均值。

3)根據公式(6)計算出未知節點到各錨節點的距離di。

4)當未知節點接收到的錨節點信息達到閾值N 時，建立以下3 個集合:

錨節點集合Sbeacon={a1，a2，…，an};錨節點位置集合Sposition={(x1，y1)，(x2，y2)，…，(xn，yn)};未知節點到錨節點的距離集合Sd={d1，d2，…，dn}。

5)對未知節點到錨節點的距離集合中的各元素按從小到大依次排序，組成新的集合;對應的新的錨節點位置集合。由2.1 節分析可知，距離值越小，測距越準確，故優選距離值較小的錨節點估計未知節點坐標，以提高定位精度。

7)根據公式(7)計算出未知節點的坐標(X，Y)。

2.6 仿真與分析

利用Matlab 軟件進行仿真。設錨節點數量為M，未知節點數量為N，錨節點和未知節點均隨機分布在室外100 m×100 m 的區域內;通信半徑r=30 m;信道衰減指數n=3.2，高斯隨機噪聲變量Xδ的標準差取為4，不考慮NLOS 誤差對定位結果的影響。

設錨節點數目為50，未知節點數目為20。圖3 為三種算法的定位誤差，對于大多數未知節點，IWCLA 的定位誤差明顯低于其它兩種CLA。

設定不同的錨節點個數，在每種錨節點個數情況下，獨立進行30 次實驗求出平均定位誤差。圖4 反映了三種定位算法平均定位誤差與錨節點數目關系。錨節點數目越多，三種定位算法的平均定位誤差越小，且IWCLA 定位效果始終優于另外二種定位算法。

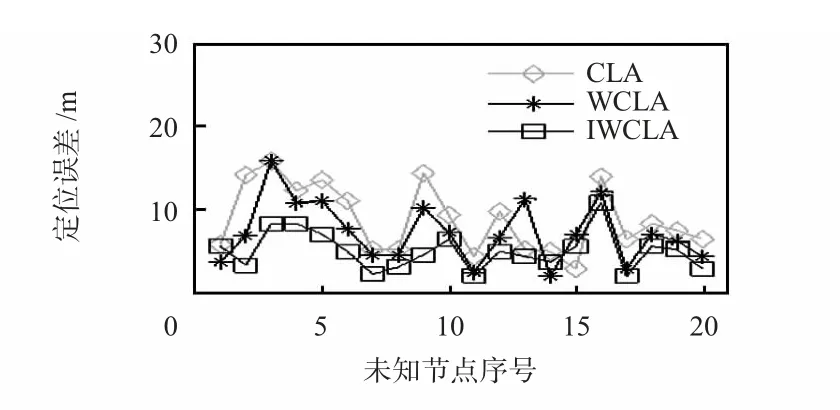
圖3 各未知節點的定位誤差Fig 3 Positioning error of each unknown node

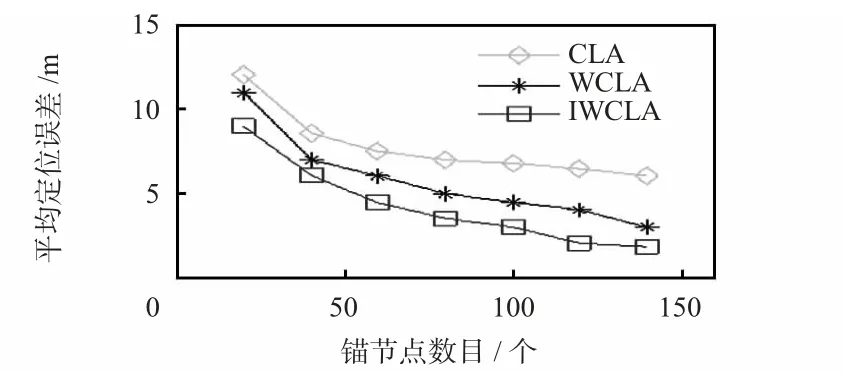
圖4 錨節點數目對定位精度的影響Fig 4 Influence of number of anchor node on positioning precision

3 IWCLA-SAN

3.1 算法描述

錨節點的數量對IWCLA 的定位精度和定位覆蓋率有很大影響，但帶有GPS 的錨節點造價是普通節點的10 倍，不適宜大規模部署。為了提高IWCLA 的定位精度和定位覆蓋率，本文將基于TDOA 測距的粒子群優化定位算法的未知節點升級為次錨節點(SAN)，再采用IWCLA 對其它未知節點進行定位。

3.2 仿真與分析

設錨節點數量為M，SAN 數為R，未知節點數量為N，錨節點、SAN 和未知節點均隨機分布在室外100 m×100 m的區域內;通信半徑r=30 m;信道衰減指數n=3.2，高斯隨機噪聲變量Xδ的標準差取為4，不考慮NLOS 誤差對定位結果的影響。

在錨節點數目有限的情況下，研究加入SAN 對定位精度的影響。設錨節點數目依次為10，20，30，40，50;SAN 數目為20;未知節點數目為20。分別獨立進行30 次實驗，求出平均定位誤差和定位覆蓋率。由圖5、圖6 可知，IWCLASAN 與IWCLA 相比可以一定程度上提高定位精度和定位覆蓋率。盡管將未知節點升級為SAN 會帶來一定的誤差累積，但基于TDOA 測距的粒子群優化無線傳感器網絡定位算法具有較高定位精度，將其作為SAN 具有一定可靠度。

4 結束語

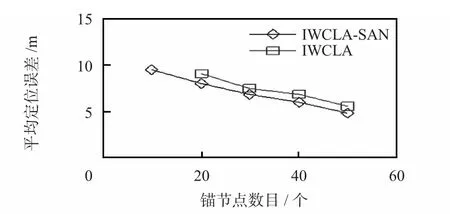
圖5 錨節點數目對定位精度的影響Fig 5 Influence of number of anchor node on positioning precision

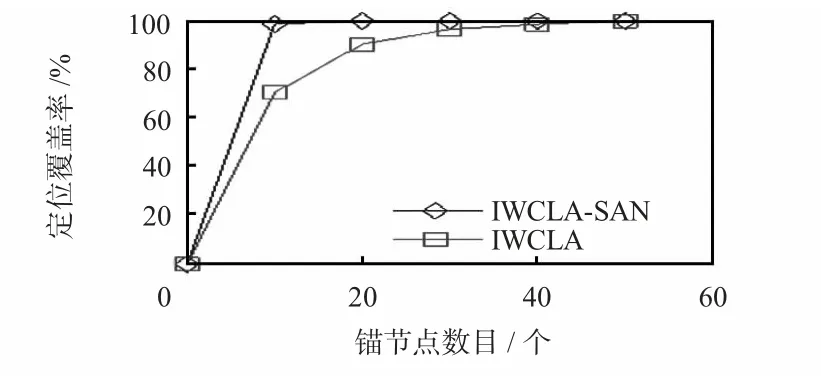
圖6 錨節點數目對定位覆蓋率的影響Fig 6 Influence of number of anchor node on localization coverage rate

本文針對定位精度較低的缺陷，在加權因子中引入了修正系數;針對CLA 對錨節點數量要求較高的缺陷，為減少錨節點數量，降低成本，將基于TDOA 測距的粒子群優化無線傳感器網絡定位算法的未知節點升級為SAN。本文提出的IWCLA 定位精度相較于WCLA 有較大提高;在錨節點數目有限的情況下，加入SAN 可以提高定位精度和定位覆蓋率。但本文并未考慮NLOS 誤差對定位精度的影響，這需進一步研究該算法在NLOS 環境中的可靠性。

［1］ 宋 文，王 兵，周應兵，等.無線傳感器網絡技術與應用［M］.北京:電子工業出版社，2007:1-10.

［2］ 孫利民，李建中.無線傳感器網絡［M］.北京:清華大學出版社，2005:135-154.

［3］ Li F F，Luo F，Wang J X，et al.An effective self-adapting localization algorithm in wireless sensor networks［J］.J of Applied Mechanics and Materials，2011，58-60:1013-1017.

［4］ Jian L R，Zheng Y，Liu Y H.Beyond triangle inequality:Sifting noisy and outlier distance measurements for localization［C］∥Proc of IEEE INFOCOM 2010，San Diego:IEEE，2010:1-9.

［5］ Kung H T，Lin C K，Lin T H，et al.Localization with snap-inducing shaped residuals:Coping with errors in measurement［C］∥Proc of MobiCom 2009，Beijing:ACM，2009:333-344.

［6］ Li Z，Trappe W，Zhang Y，et al.Robust statistical methods for securing wireless localization in sensor networks［C］∥Proc of IPSN 2005，Los Angeles:IEEE，2005:91-98.

［7］ Zhang Q X，Di Q L，Xu G Y，et al.A RSSI-based localization algorithm for multiple mobile robots［C］∥Proc of CMCE 10，Changchun:IEEE，2010:190-193.

［8］ 李曉維，徐勇軍，任豐原.無線傳感器網絡技術［M］.北京:北京理工大學出版社，2007:191-199.

［9］ 彭 宇，王 丹.無線傳感器網絡定位技術綜述［J］.電子測量與儀器學報，2011，25(5):389-399.

［10］方 震，趙 湛，郭 鵬，等.基于RSSI 測距分析［J］.傳感技術學報，2007，20(11):2526-2530.

［11］王曉樂，徐家品.基于粒子群優化算法的WSNs 節點定位研究定位［J］.計算機應用，2009，29(2):494-499.

［12］邢明彥，李臘元.粒子群優化算法在無線傳感器網絡中的應用［J］.計算機工程與應用，2009，45(32):72-74.

［13］陳維克，李文鋒，首 珩，等.基于RSSI 的無線傳感器網絡加權質心算法定位［J］.武漢理工大學學報，2006，30(2):265-268.

［14］Chen W，Mei T，Sun L，et al.Error analyzing for RSSI-based localization in wireless sensor networks［C］∥7th World Congress on Intelligent Control and Automation，WCICA 2008，IEEE，2008:2701-2706.

［15］楊新宇，孔慶茹，戴湘軍.一種改進的加權質心定位算法［J］.西安交通大學學報，2010，44(8):1-4.