一種基于SC-FDMA系統(tǒng)改進的LMMSE信道估計算法*

2015-03-25 05:16:14欒亞婷闞春榮杜昊陽

通信技術(shù) 2015年9期

欒亞婷，闞春榮，杜昊陽

(解放軍理工大學(xué)通信工程學(xué)院國家短波工程中心,江蘇南京 210007)

欒亞婷，闞春榮，杜昊陽

(解放軍理工大學(xué)通信工程學(xué)院國家短波工程中心,江蘇南京 210007)

對于LTE上行鏈路來說，尋求性能優(yōu)良的信道估計算法是十分必要的。傳統(tǒng)的最小平方(LS)和線性最小均方誤差(LMMSE)信道估計算法存在許多不足。其中，在研究過程中會發(fā)現(xiàn)傳統(tǒng)線性最小均方誤差(LMMSE)信道估計算法具有計算復(fù)雜度大的問題。然而，通過借助于雅克比迭代算法解決線性方程的理念，能夠?qū)鹘y(tǒng)的LMMSE算法做進一步的改進。同時，理論分析和仿真結(jié)果表明：該算法在低信噪比下表現(xiàn)出良好的性能，它不僅降低了計算復(fù)雜度，而且估計結(jié)果更精確。

信道估計；LMMSE算法；雅克比迭代

0 引言

在移動通信的快速發(fā)展中，LTE 技術(shù)將在通信領(lǐng)域占據(jù)越來越重要的位置[1]。針對未來通信的需求，為了降低峰平比，SC-FDMA已經(jīng)成為LTE上行鏈路的關(guān)鍵技術(shù)，而對于上行鏈路來說，研究信道估計是十分必要的。

在無線通信系統(tǒng)中，信道估計結(jié)果對接收機端的性能有著直接的影響。基于此，眾多學(xué)者研究出了各種各樣的信道估計算法，就總體而言，信道估計主要分為兩種：盲信道估計和非盲信道估計。實際中，我們主要采用基于導(dǎo)頻的非盲信道估計。傳統(tǒng)的估計算法主要有LS算法和LMMSE算法。其中LS算法操作最簡單，但是由于它忽略了噪聲的影響，在信道環(huán)境糟糕的情況下，它的性能就會急劇下降；LMMSE算法在增加復(fù)雜度的基礎(chǔ)上考慮了噪聲的影響，表現(xiàn)出比較優(yōu)越的性能，估計結(jié)果更為精確。所以LMMSE 算法在未來通信發(fā)展過程中存在著一定的優(yōu)勢，是值得我們深入研究的。傳統(tǒng)的基于奇異值分解(SVD)的低秩估計算法是利用信道的頻域或時域的相關(guān)性以及奇異值分解技術(shù)對LMMSE算法進行近似處理，降低了運算復(fù)雜度。因此，為了提高通信質(zhì)量，我們必須提出一種不僅操作簡便而且性能優(yōu)良的信道估計算法。依據(jù)文獻[2]，一種基于雅克比迭代改進的LMMSE算法被提出，該改進算法在低信噪比下不僅計算復(fù)雜度降低，而且估計結(jié)果也更為精確。

1 LTE上行鏈路系統(tǒng)模型

LTE的上行多址接入采用單載波頻分多址(SC-FDMA)方案，為了提高帶寬效率，使用DFT擴展OFDM生成SC-FDMA。在LTE上行傳輸資源結(jié)構(gòu)中，一個10 ms的無線幀被分成10個1 ms的子幀，每個子幀包含兩個0.5 ms的時隙，子載波間隔和下行鏈路一樣為15 kHz[3]。

SC-FDMA系統(tǒng)模型如圖1所示。

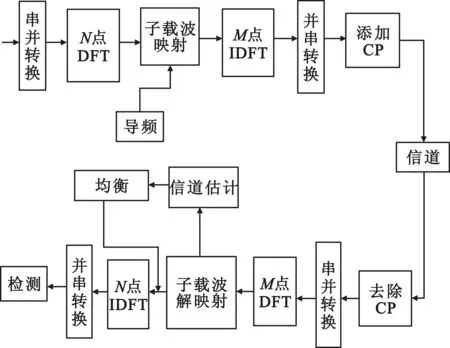
圖1 SC-FDMA系統(tǒng)

其中，在LTE上行鏈路中存在兩種子載波映射方式：集中式子載波映射和分布式子載波映射[3]。在此僅介紹一下仿真中采用的集中式子載波映射。如圖2所示：

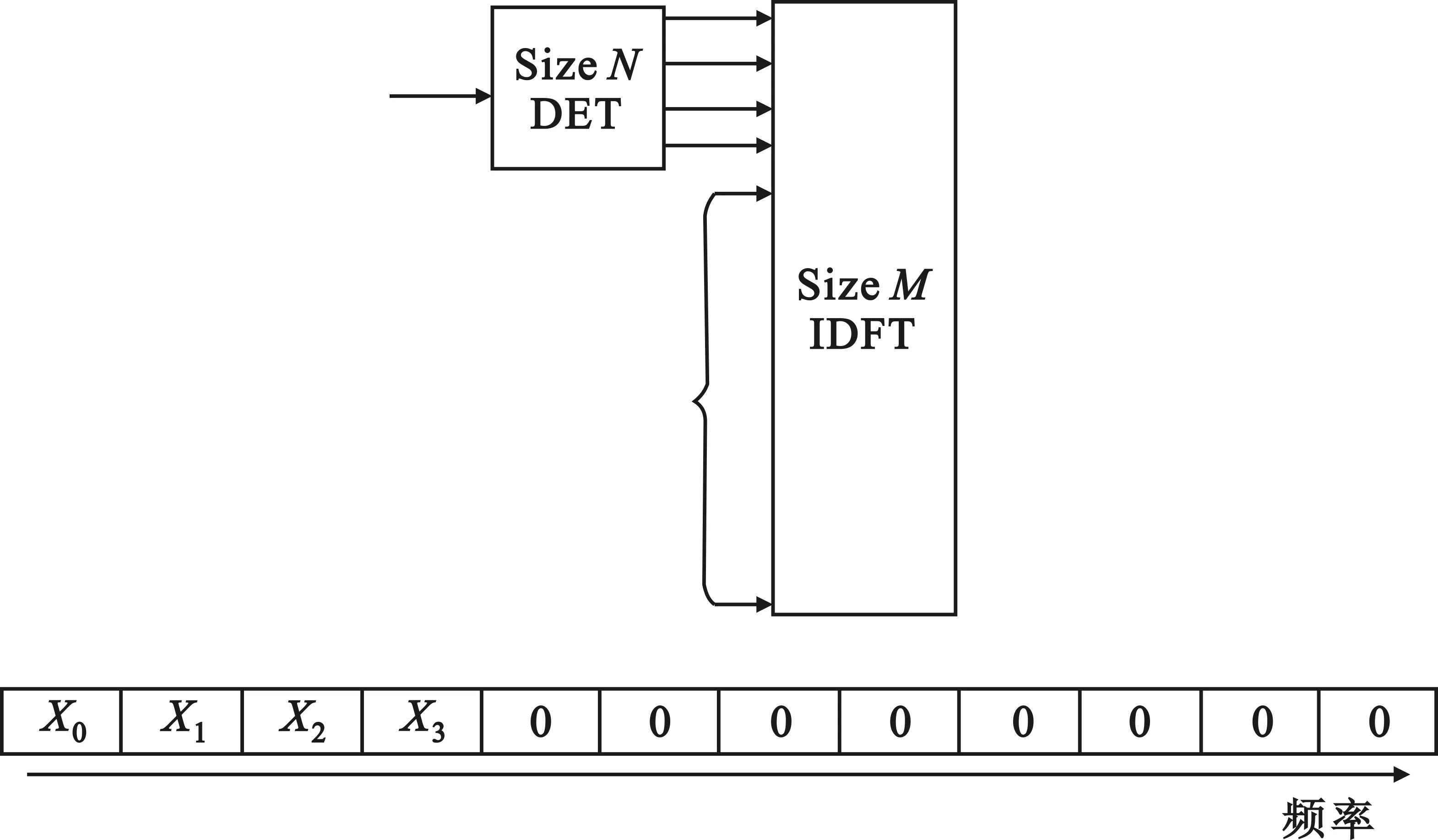
圖2 集中式子載波映射

LTE的上行導(dǎo)頻信號大多都是基于Zadoff-Chu(ZC)序列[4]。其中導(dǎo)頻序列的長度等于用戶子載波數(shù)，如果導(dǎo)頻序列的長度(Np)為奇數(shù)，它可以被定義為：

(1)

式中，q=1,2，…,NZC-1是ZC序列的索引，n=0,1,…,NZC-1，并且在LTE中，l通常取值為0。一般來說，在LTE中，NZC應(yīng)為小于或等于Np的最大質(zhì)數(shù)[4]。長度為NZC的ZC序列可以按照如下方式擴展成長度Np，即

(2)

通常，導(dǎo)頻插入方式有塊狀、梳狀和菱形狀[5-6]，其中在LTE上行鏈路中我們一般采用塊狀導(dǎo)頻插入方式，其插入方式如圖3所示。

圖3 塊狀導(dǎo)頻插入

2 信道估計算法

假定在接收端不存在同步誤差，則接收端的頻域信號可表示為：

Yi,k=Hi,kXi,k+Wi,kk=0,1,…N-1

(3)

式中，i表示接收到的第i個SC-FDMA 符號，k表示第i個SC-FDMA 符號上的第k個子載波，N表示總的子載波數(shù)[7]。在LTE上行鏈路中，我們通常是得出導(dǎo)頻處的信道估計結(jié)果，再根據(jù)導(dǎo)頻信道估計結(jié)果去對數(shù)據(jù)符號進行估計。下面分別介紹幾種傳統(tǒng)信道估計算法和改進的LMMSE算法。

2.1 LS算法

LS算法的估計準則就是確保接收到的信號和理想信號之間的距離的平方最小[8]，即

(4)

根據(jù)最小平方準則，導(dǎo)頻處的LS信道估計算法可以表示為：

(5)

LS算法盡管操作簡單，計算復(fù)雜度低，但是沒有考慮噪聲和子載波間干擾的影響，估計結(jié)果不是很理想。

2.2 LMMSE算法

LMMSE算法其實就是優(yōu)化的MMSE算法。而MMSE算法考慮到了噪聲的影響，其估計準則是使實際的信道脈沖響應(yīng)和理想的信道脈沖響應(yīng)的均方誤差最小[8]。LMMSE估計準則如下：

(6)

方程(6)可以被簡化為

(7)

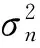
(8)

式中，I是單位矩陣。信噪比為：SNR=EX2/σ2，所以LMMSE估計可以表示為：

(9)

式中，β的取值與調(diào)制方式有關(guān)，當調(diào)制方式為QPSK時，β取為1，16QAM時β為17/9。但是，LMMSE算法需要求逆矩陣，這就加大了計算復(fù)雜度[9]。針對該缺陷，人們提出了基于SVD分解的降秩方法，信道的自相關(guān)矩陣可以表示為：

RHH=UΛUH

(10)

這里的U為酉矩陣，Λ=diag(λ0,λ1,…,λNP-1),它是由RHH由大到小的特征值排列構(gòu)成的對角矩陣，則基于SVD分解的降秩估計結(jié)果為：

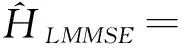
(11)

在方程(11)中：

(12)

其中，m為低秩的階數(shù)，一般取為循環(huán)前綴的長度。

2.3 改進的LMMSE算法

為了進一步改進LMMSE算法的性能，我們提出了一種基于雅克比迭代的LMMSE算法，改進的算法在低信噪比下不僅性能有所提升，并且估計結(jié)果也更為準確。由文獻[2]可知雅克比迭代算法如下：

假定線性方程Ax=b，即：

(13)

其中A是非奇異矩陣，并且aii≠0,i=1,2,…,n，則可以得到：

(14)

相應(yīng)的迭代方程為：

(15)

這里k代表迭代次數(shù)。

令A(yù)=D-L-U,L是下三角矩陣，U是上三角矩陣。

則方程Ax=b可以被表述為：

x(k+1)=D-1(L+U)x(k)+D-1b

(16)

其中B=D-1(L+U)，f=D-1b，這就是雅克比迭代算法。在迭代期間，我們可以設(shè)置初始值和終止條件。

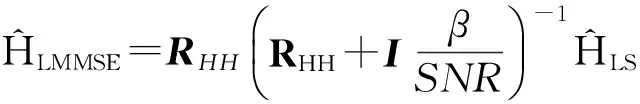
(17)

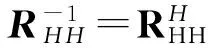
(18)

其中RHH是與信道統(tǒng)計特性相關(guān)的矩陣。但是在實際中我們通常無法準確了解信道的統(tǒng)計知識，在仿真中，我們一般采用服從指數(shù)分布的功率延遲來模擬實際信道。

(19)

(20)

RHH是正規(guī)矩陣，由式(19)可得：

(21)

其中R(0)=1,并且R(i)=R*(-i)，所以可得：

3 仿真結(jié)果和分析

該仿真環(huán)境設(shè)置為LTE上行鏈路，其仿真參數(shù)在表1中給出。

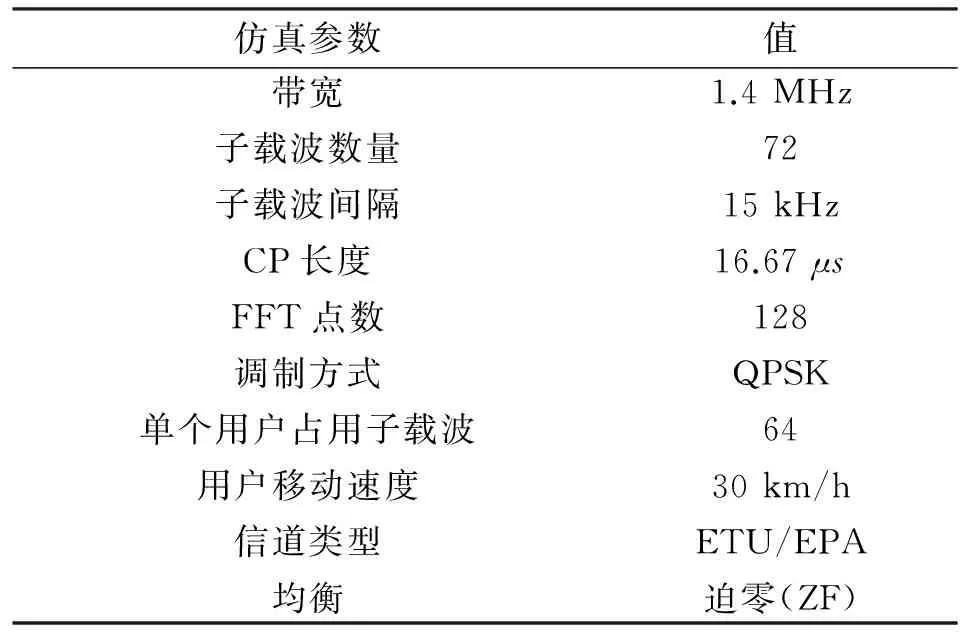
表1 仿真參數(shù)

其中ETU和EPA信道參數(shù)分別如表2和表3所示。

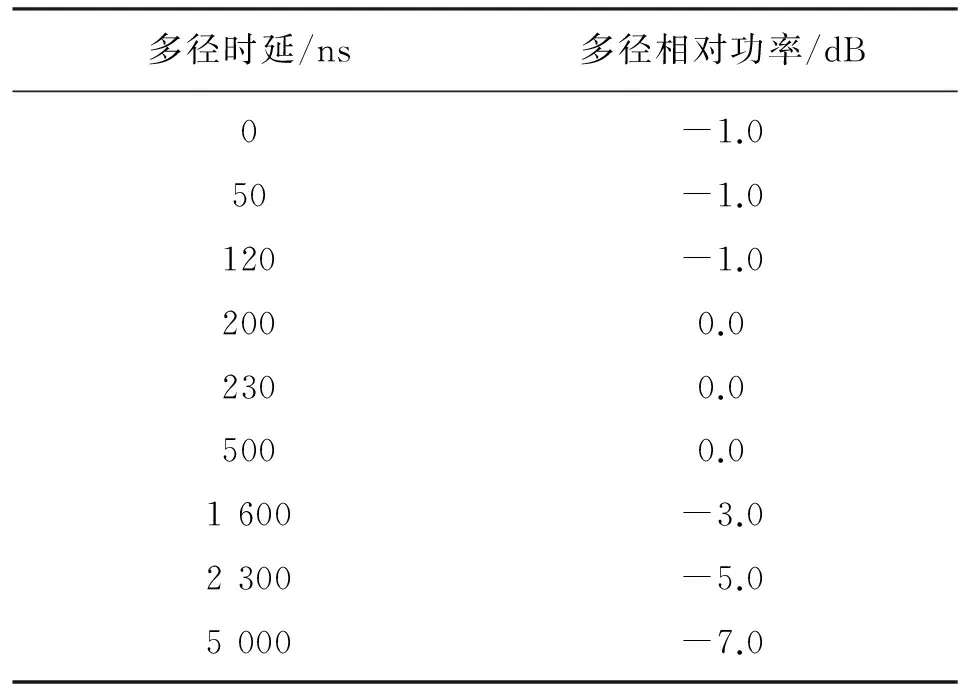
表2 ETU信道參數(shù)

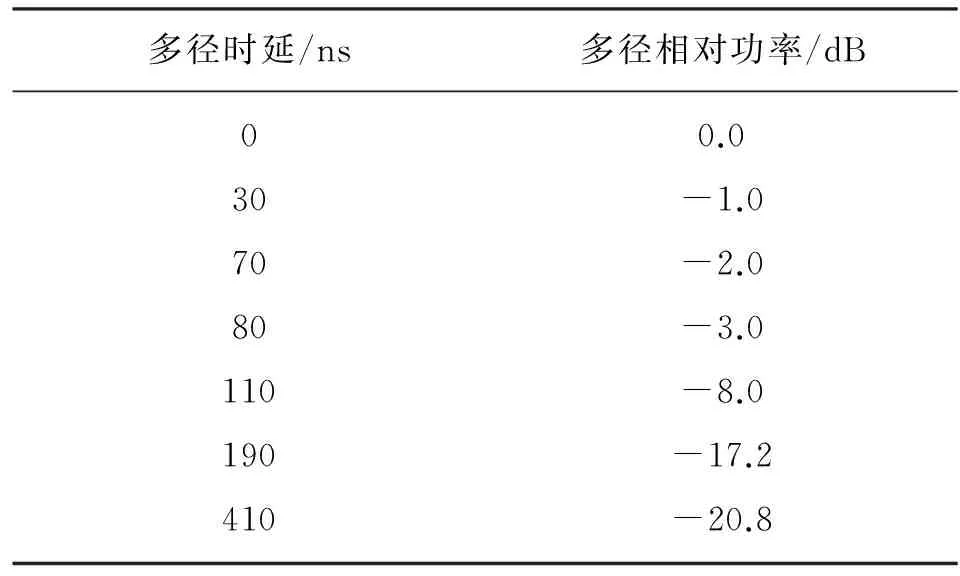
表3 EPA信道參數(shù)

仿真過程：

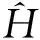
(3) 用導(dǎo)頻處的信道響應(yīng)估計出該時隙內(nèi)數(shù)據(jù)位置處的符號。

仿真結(jié)果如圖4和圖5所示。

圖4 ETU信道估計誤碼率性能曲線

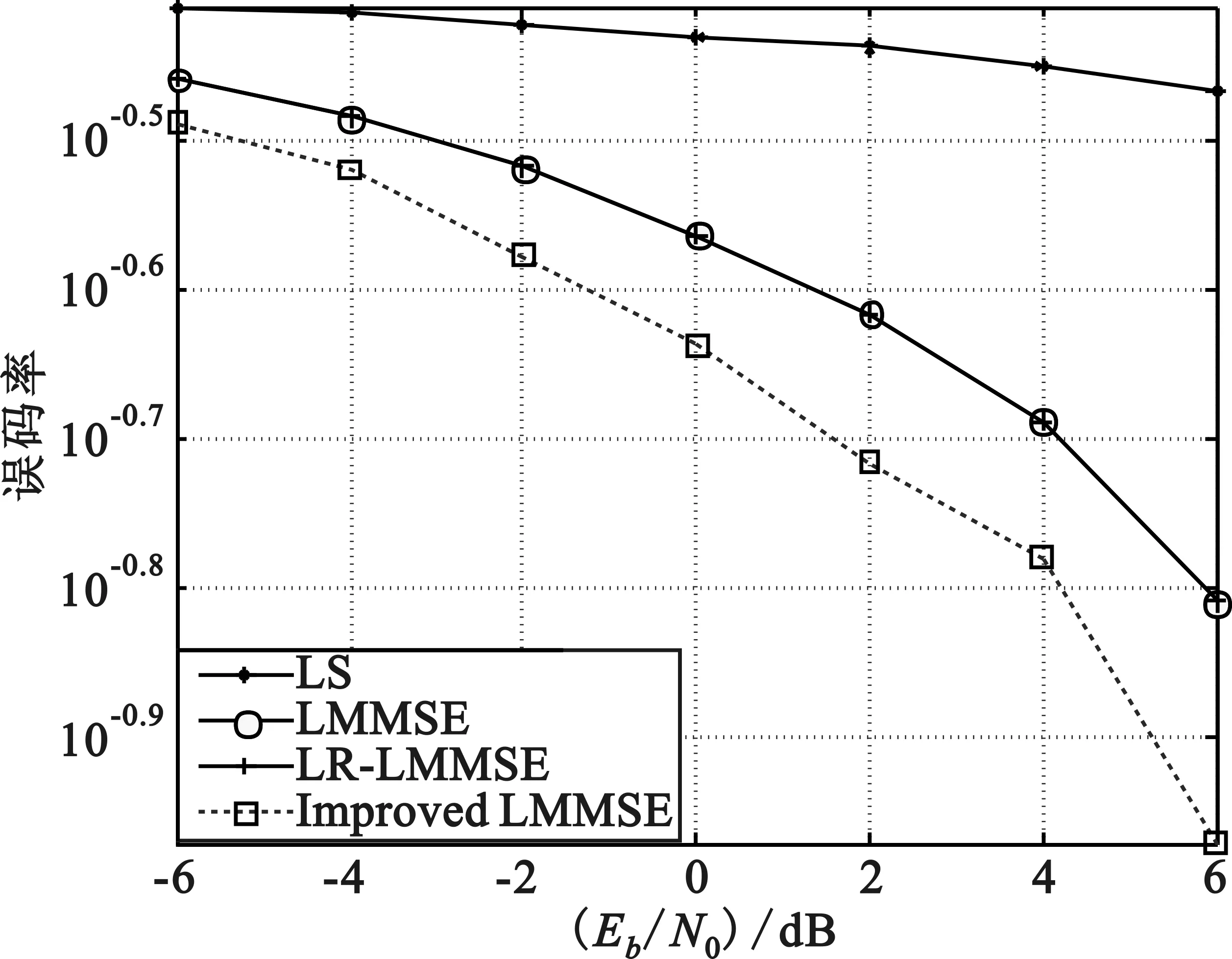
圖5 EPA信道估計誤碼率性能曲線

在實際中，我們以誤碼率作為評價準則[10]，圖4和圖5為誤碼率性能比較。從圖中可以看出我們提出的改進的LMMSE算法的性能在低信噪比的情況下性能是最好的，LS算法是最差的，而LMMSE算法和基于SVD分解的LR-LMMSE算法的性能沒有太大的差別，但性能略遜于我們提出的算法。

我們以估計一個導(dǎo)頻符號處的信道響應(yīng)為例，進行算法復(fù)雜度的比較。若用雅克比迭代改進的LMMSE算法計算，每次迭代只需計算一次矩陣和向量的乘法。設(shè)導(dǎo)頻長度為Np，迭代次數(shù)為1，則改進的LMMSE算法和傳統(tǒng)的LMMSE算法復(fù)雜度對比如表4所示。

表4 算法復(fù)雜度對比

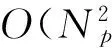
4 結(jié) 語

本文針對傳統(tǒng)的LMMSE算法，通過借助雅克比迭代算法求解線性方程組的理念，從一定程度上改進了傳統(tǒng)的LMMSE算法。理論驗證和仿真結(jié)果表明：改進的LMMSE算法的復(fù)雜度遠低于傳統(tǒng)的LMMSE算法，并且占用的硬件存儲空間也將降低，在低信噪比下其估計結(jié)果也更加精確。但是，未來如何在高信噪下針對LMMSE算法進行改進，還有待進一步研究。

[1] ZHOU Mei-li, JIANG Bin, GAO Xi-qi. Efficient Channel Estimation for LTE Uplink[C]. IEEE Wireless Communications & Signal Processing,2009:1-5.

[2] YI Xue, Numerical Analysis and Experiment[M]. Beijing Industrial University Press, March 2005.

[3] Stefania Sesia, Issam Toufik, Matthew Baker, LTE-The UMTS Long Evolution: From Theory to Practice[M]. Posts & Telecom Press, Dec 2009.

[4] WEN Yang, HUANG Wei, ZHANG Zhong-pei. CAZAC Sequence and Its Application in LTE Random Access[J].IEEE Information Theory Workshop, 2006:544-547.

[5] LI Ye. Pilot-Symbol-Aided Channel Estimation for OFDM in Wireless Systems[J]. IEEE Transaction on Vehicular Technology, 2000 July,49(4):1207-1214.

[6] Dae-Hong Lee, Se-Bin Im. Hyung-Jin Choi.A Novel Pilot Mapping Method for Channel-Quality Estimation in SC-FDMA System[C].Asia-Pacific Conference on Communications, 2007:307-310.

[7] Karakaya B and Arslan H. Channel Estimation for LTE Uplink in High Doppler Spread[C]. In Proc. WCNC, Mar.2008:1126-1130.

[8] LIU Wen-wen, LI Xiao-lin. An Improved LMMSE Channel Estimation Algorithm Of LTE System[C]. ICCIS,2012:231-234.

[9] Omar, Ancora S, Slock A. D.T.M.Performance Analysis of General Pilot-Aided Linear Channel Estimation in LTE OFDMA Systems with Application to Simplified MMSE Schemes[C]. IEEE 19th International Symposium on Personal, Indoor and Mobile Radio Communications,2008:1-6.

[10] K. Oh, Impact of Channel Estimation Error in Adaptive Wireless Communication Systems[M]. MS Dissertation, Polytechnic University, Jun.2006.

A Modified LMMSE Channel Estimation Algorithm for SC-FDMA

LUAN Ya-ting, KAN Chun-rong, DU Hao-yang

(State Shortwave Engineering Center, PLA University of Science and Technology, Nanjing Jiangsu 210007, China)

The channel estimation algorithm with excellent performance is essential for LTE (Long Term Evolution) uplink. Many defects usually exist in the traditional LS (Least Square) algorithm and LMMSE (Liner Minimum Mean-Square) algorithm. Research on the traditional LMMSE algorithm indicates its fairly large complexity. And with Jacobi iterative algorithm for solving linear equations, the traditional IMMSE algorithm could be further improved. Meantime theoretical analysis and simulation results show that the modified LMMSE algorithm performs fairly well at low SNR,and could reduce the computational complexity while achieving more precise estimation result.

channel estimation；LMMSE algorithm；Jacobi iterative algorithm

2015-03-20；

2015-07-05 Received date:2015-03-20；Revised date：2015-07-05

TN 929.5

1002-0802(2015)09-1015-05