采用確定性測量矩陣的寬帶壓縮采樣的研究*

王學玲,王華力,曾顯華,郭克鋒,孫久皓

(1.解放軍理工大學 通信工程學院 江蘇 南京 210007；2.遼寧沈陽鐵西區65040部隊 遼寧 沈陽 110005)

采用確定性測量矩陣的寬帶壓縮采樣的研究*

王學玲1,王華力1,曾顯華1,郭克鋒1,孫久皓2

(1.解放軍理工大學 通信工程學院 江蘇 南京 210007；2.遼寧沈陽鐵西區65040部隊 遼寧 沈陽 110005)

在對寬帶信號進行處理的過程中，常運用壓縮感知的理論來獲得有效的信息。而在實踐壓縮感知理論的壓縮采樣的結構中，調制寬帶轉換器的采樣結構更加適合用于處理寬頻帶信號。文中研究了調制寬帶轉換器的壓縮采樣原理，也介紹了隨機測量矩陣和確定性測量矩陣。分別將隨機矩陣和確定性矩陣作為該調制寬帶轉換器的測量矩陣，對比分析了該采樣結構的重構性能。研究了在確定性測量矩陣的基礎上，該采樣結構在折疊和非折疊條件下的信號重構性能，同時，也對系統的通道數目對性能重構和信噪比的影響進行了補充分析。

壓縮采樣；寬帶信號；調制寬帶轉換器；壓縮感知；測量矩陣

0 引 言

隨著信息技術的高速發展，為了滿足信息獲取的需求，需要對寬帶信號進行處理。若根據傳統的Nyquist采樣定理對寬帶信號進行信息提取，會由于硬件的限制，很難實現。所以，需要采用新的處理方式對寬帶信號進行處理。2006年，D. Donoho、E. Candes和T. Tao等人提出了壓縮感知(Compressed Sensing，CS)理論[1-3]。根據此理論，在對寬帶信號進行處理時，將具有有效信息的帶寬先壓縮，再采樣，在壓縮采樣后的信號中再獲得有效的信號。

在壓縮采樣的過程中，最先實現壓縮采樣的結構是隨機采樣(Random Sampling，RS)結構。其基本原理是利用采樣時鐘上的隨機性，使得每個采樣值都保持不同程度的頻譜信息。隨后，S. Kriolos等提出了隨機解調器(Random Demodulation，RD)[4]結構。Y. C. Eldar等提出了基于稀疏多帶模型的調制寬帶轉換器(Modulated Wideband Converter，MWC)結構。此外，目前壓縮采樣結構中的基于Sigma-Delta量化的模擬/信息轉換器[5]、非線性仿射編解碼(Nonlinear Affine Encoding/Decoding，NoLAff)結構[6]、時間編碼器(Time-Encoding Machine，TEM)結構[7]等仍處在研究中。

本文首先對調制寬帶轉換器的壓縮采樣[13-14]進行了研究，并對測量矩陣的內容進行了分析介紹。突出對比了隨機矩陣和確定性矩陣分別作為測量矩陣時，MWC系統的信號重構的效果。同時，在確定性矩陣作為系統測量矩陣的基礎上，顯著地對比分析了折疊和非折疊條件下，MWC系統的信號重構性能，也完整地研究了在非折疊條件下，MWC系統的通道數目對信號重構和信噪比的影響。其中，通過對比仿真分析，兼顧硬件實現的考慮，在確定性測量矩陣條件下，利用折疊的方式也可以達到很好的重構效果。

1 調制寬帶轉換器的寬帶壓縮采樣

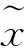
(1)

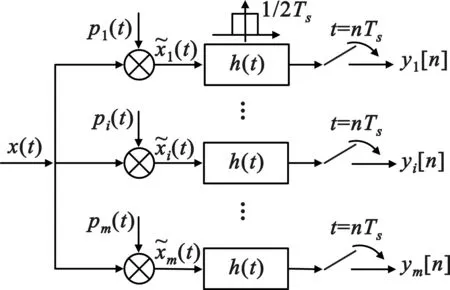
圖1 調制寬帶轉換器的結構

MWC中，輸入信號x(t)如圖2中上半部分所示。子帶帶寬為B，子帶個數為N，其中，fmax=N×B，且每個子帶信號的形式可以是任意形式的信號，如AM、FM、QAM信號等。圖2描述了稀疏多帶信號的頻譜壓縮測量。稀疏多帶輸入信號與周期信號pi(t)的混頻操作混疊了輸入信號x(t)的頻譜，使得所有頻帶的一部分能量出現在基帶。此外，混頻的結果是把各個頻帶以lfp的頻率調制到低頻段疊加起來，權重系數是傅立葉系數cil。

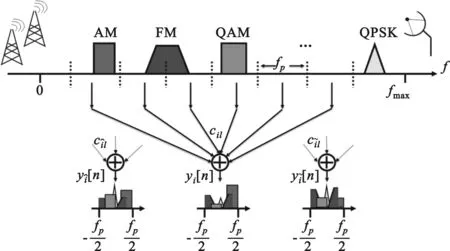
圖2 稀疏多帶信號的頻譜壓縮測量

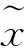
通過低通濾波器之后，信號頻譜已被調制壓縮到低頻段，普通的ADC器件就可以實現壓縮頻譜信號的低速率采樣，但此時ADC的采樣速率必須保證對調制濾波后信號的Nyquist 采樣，即fs≥fp。由于采用了低速率的ADC和便宜的RF混頻器從而允許以較低成本實現寬頻帶信號的壓縮采樣。

在MWC對寬帶信號進行壓縮采樣的過程中，測量矩陣的研究是核心內容之一。在測量矩陣的研究中，確定性測量矩陣和隨機測量矩陣的研究具有重要的研究價值。

2 測量矩陣

在調制寬帶轉換器系統的性能重構仿真中，作為測量矩陣的調制序列的選擇極為關鍵。目前，常用的測量矩陣大致可以分成隨機測量矩陣和確定性測量矩陣兩大類。隨機測量矩陣包括高斯隨機測量矩陣、伯努利隨機測量矩陣、部分正交測量矩陣、稀疏隨機測量矩陣等。隨機測量矩陣的共同特點是測量矩陣中的元素相互獨立且服從同一隨機分布。

本文提出了一個單層神經網絡模型用于求解含約束的l1-范數問題。與已有求解問題(1)的神經網絡模型相比,提出的模型需要神經元數少且層數少。利用Lyapunov函數,證明了該模型的Lyapunov穩定性和漸近穩定性。數值試驗結果表明,提出的模型具有良好性能且可以用于圖像恢復問題。

然而，隨機測量矩陣中的各個元素的產生具有隨機性，因而在產生隨機測量矩陣的過程中需要較大的存儲空間和較高的計算量。所以，在實際的壓縮采樣電路中，并不常使用隨機測量矩陣。

目前，壓縮采樣處理過程中采用的測量矩陣大多數為隨機測量矩陣，而隨機測量矩陣通常具有一定的隨機性，并且在硬件實現上具有一定的困難。在壓縮采樣處理過程中采用的測量矩陣大多并不是任意隨機的，而是確定的隨機矩陣，這類矩陣既具有隨機矩陣的一些特性，如性能不穩定，也包含了確定性測量矩陣的確定性。確定性測量矩陣是根據某一特定信號而構造的，例如，循環測量矩陣是由m序列構成的矩陣。相對于隨機測量矩陣，確定性測量矩陣的最大優點是測量矩陣的確定性和穩定性。其缺點在于重構效果沒有隨機測量矩陣好，且所需要的最小測量維度較多。

確定性測量矩陣主要包括Toeplitz矩陣、循環測量矩陣、多項式確定性矩陣、二值稀疏矩陣等。常用的確定性測量矩陣為Toeplitz矩陣和循環測量矩陣，其構造方式為：首先生成一個向量：

u=(u1,u2,…,uN)∈RN

(2)

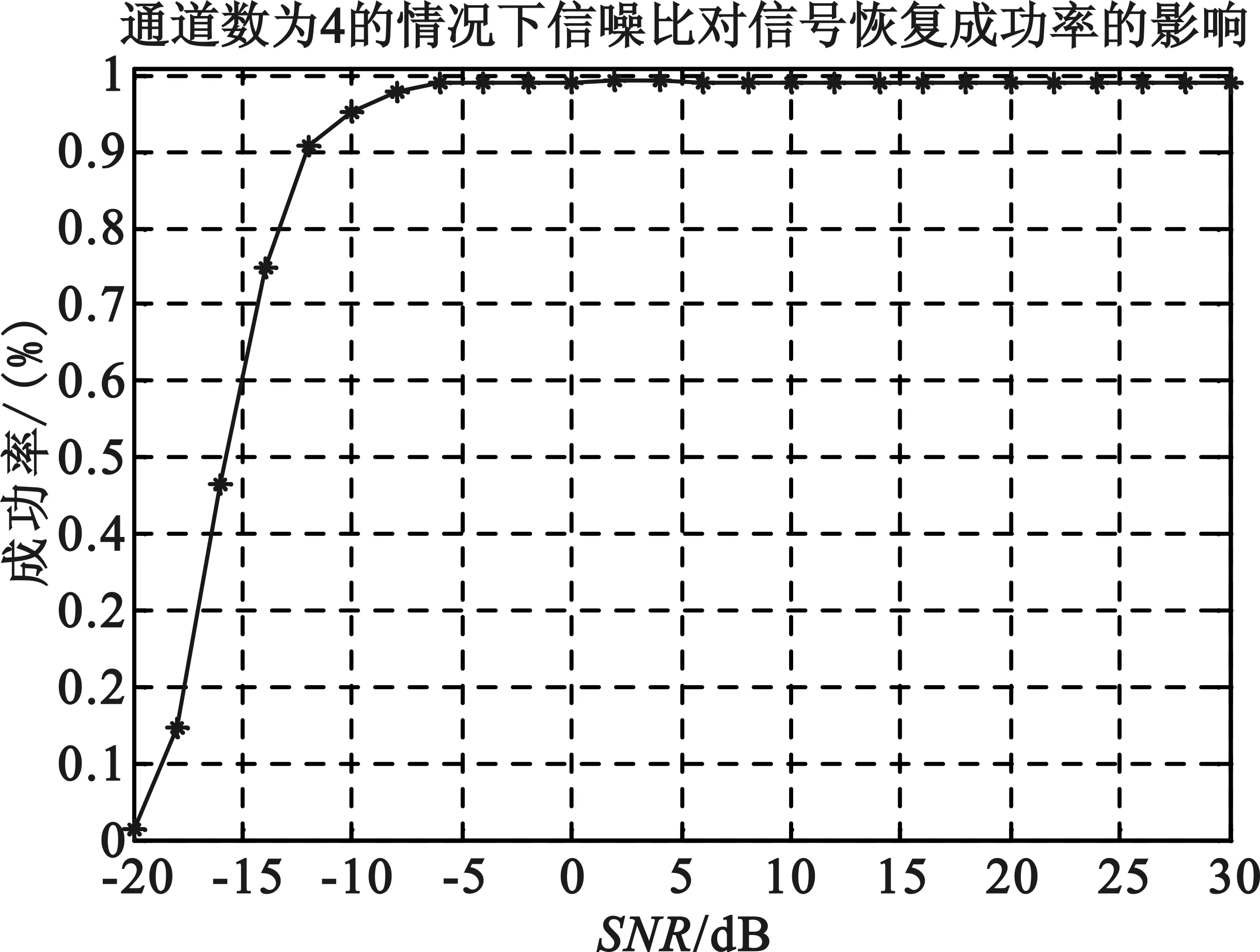
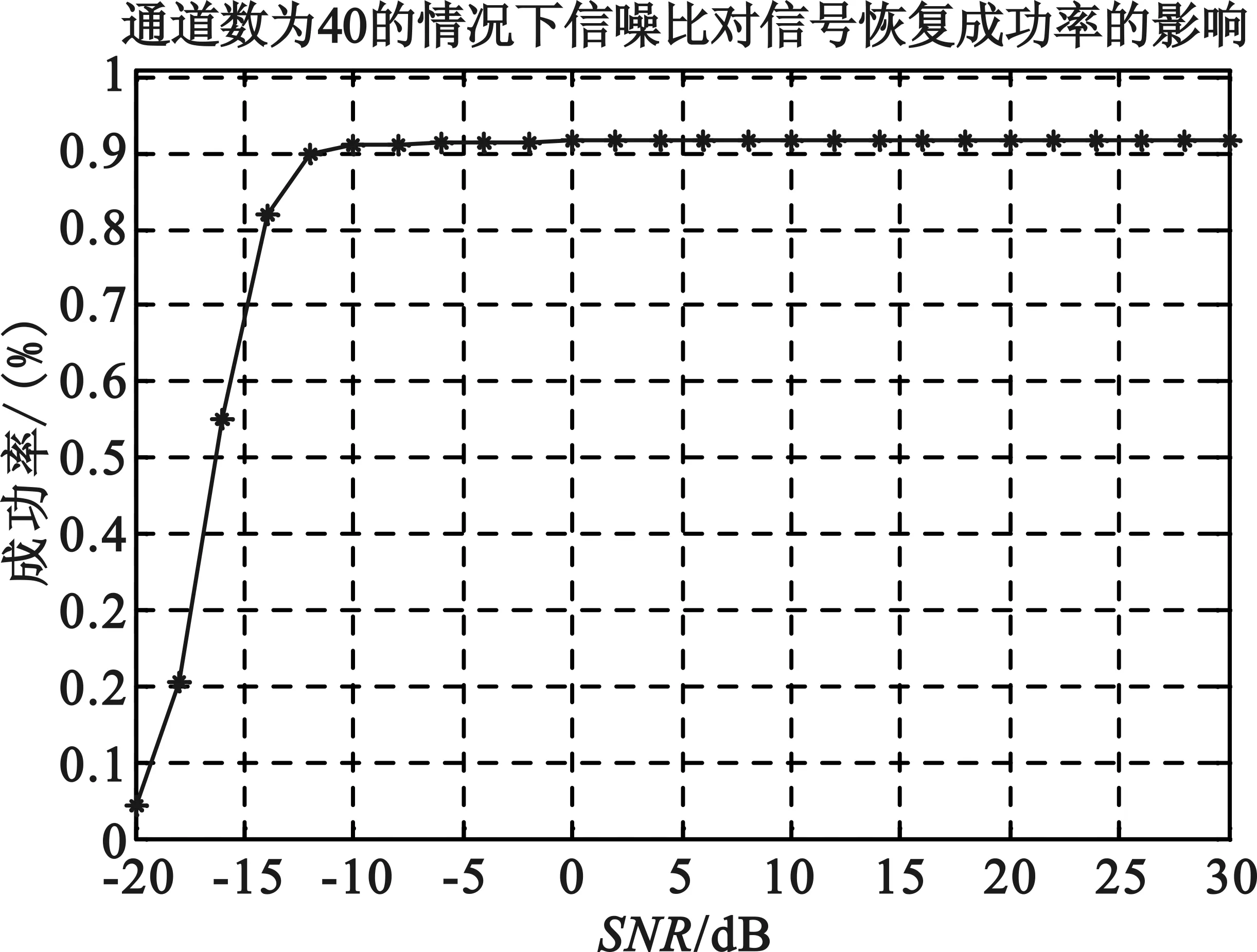
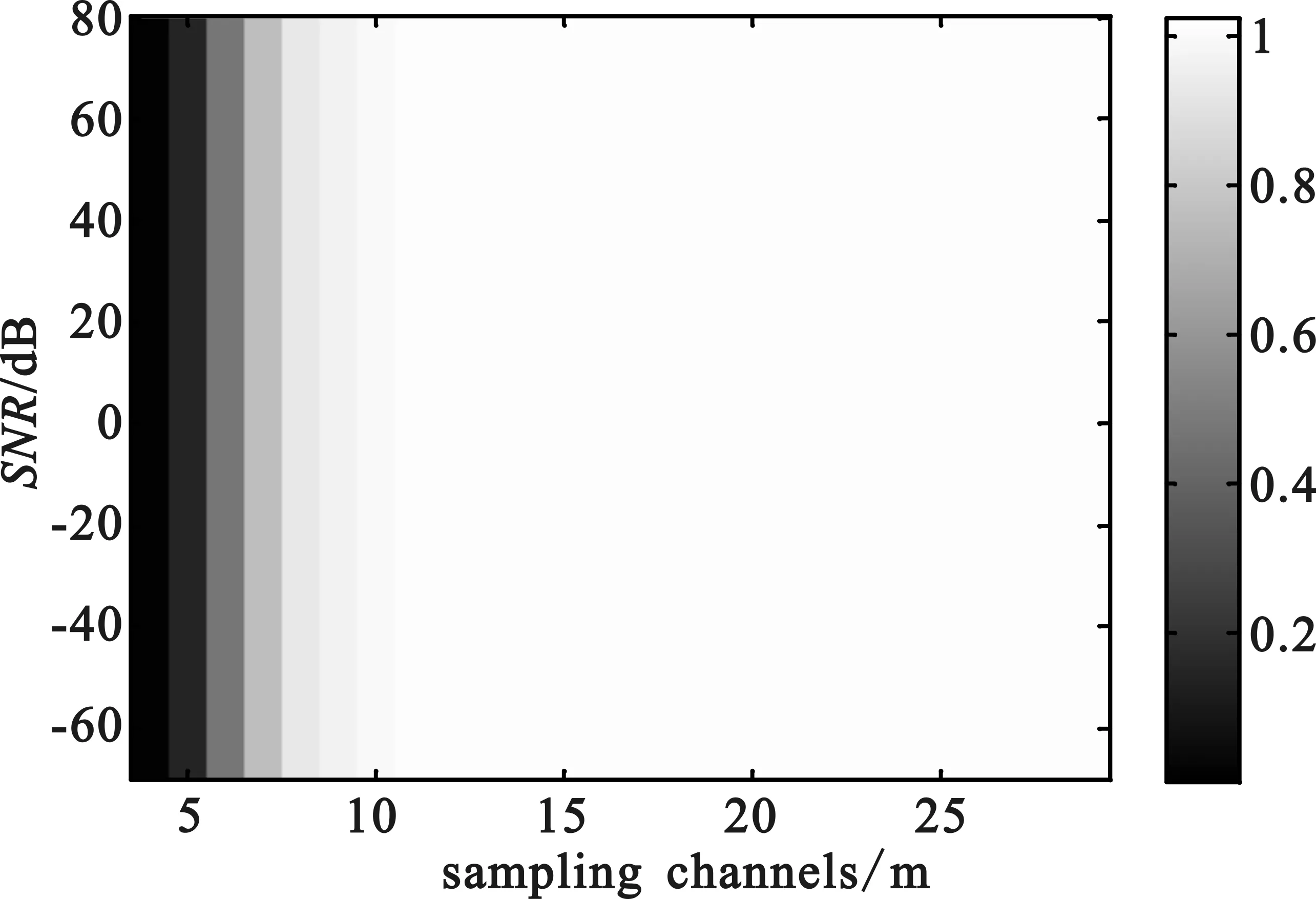
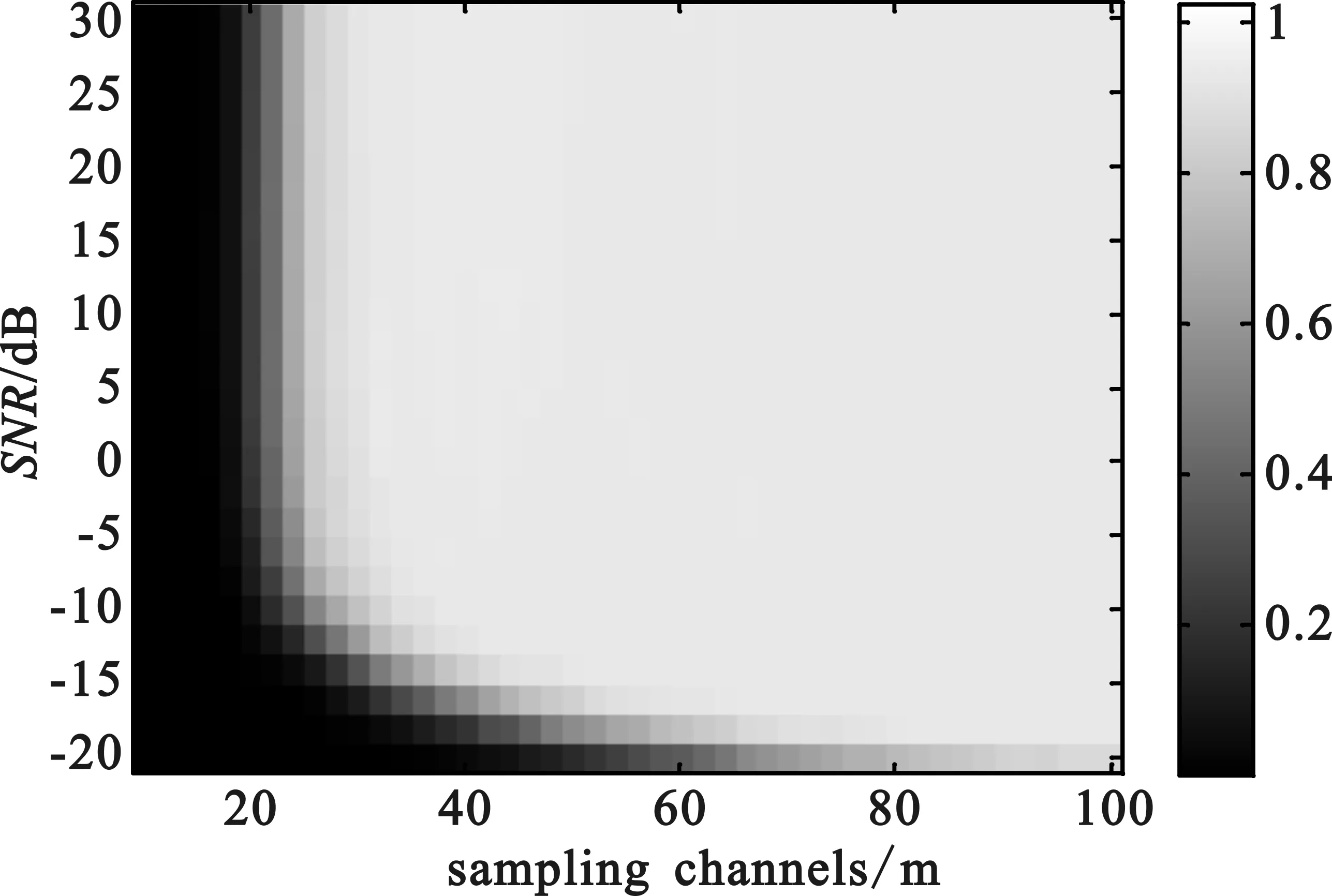
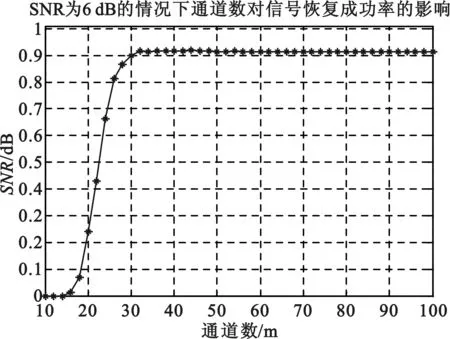
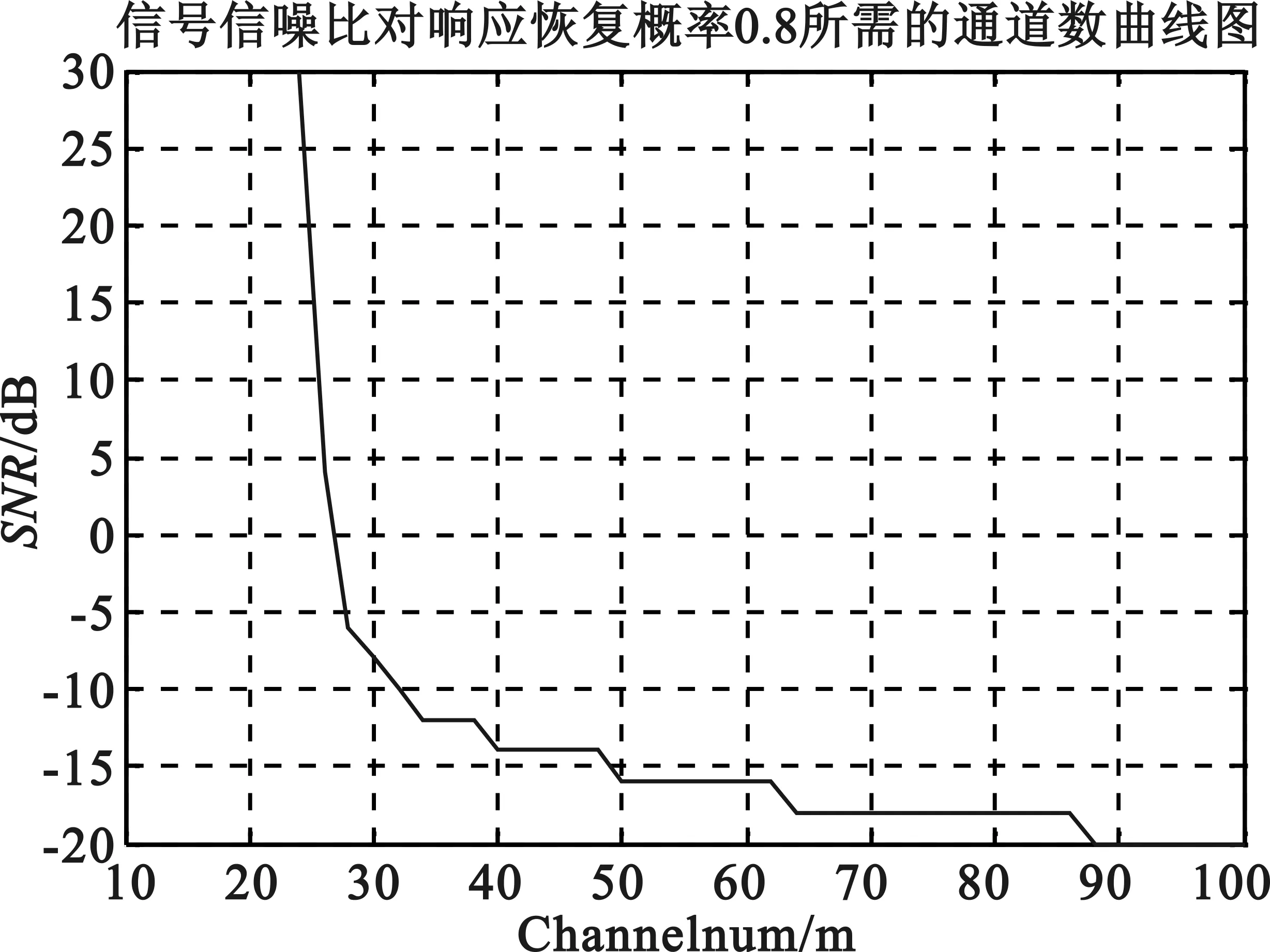
由向量u通過M(M

Toeplitz測量矩陣和循環測量矩陣通過采用行向量的循環移位的方式生成矩陣中所有的元素。也正是因為這種循環移位產生序列的方式便于硬件的實現，使得Toeplitz矩陣和循環測量矩陣能夠被廣泛地研究和應用。

3 性能仿真

MWC系統性能的仿真過程中，調制序列的選擇至關重要。MWC系統仿真參數分別為：折疊系數q=11，奈奎斯特采樣速率fnyq=480 MHz，輸入寬頻帶信號的子帶個數N=12，子帶寬度B=0.8 MHz，系統通道數目m=4。其中，序列seq127，seq255，seq511采用循環測量矩陣，而序列seq189則采用伯努利隨機測量矩陣。MWC采用隨機測量矩陣與確定性測量矩陣的性能重構仿真如圖3所示。

圖3 MWC重構性能的仿真

從仿真結果中可知：在4個系統采樣通道條件下，要達到90%的精確重構概率，調制序列分別為seq127，seq189，seq255，seq511的信號時，信噪比至少要分別達到-12 dB，-12 dB，-10 dB，-8 dB。同時，采用確定性測量矩陣的MWC系統的重構性能非常接近于隨機測量矩陣的重構性能，考慮硬件實現方面的因素，在實踐中可以考慮采用確定性測量矩陣代替隨機測量矩陣。

MWC系統在采用確定性測量矩陣時，在折疊系數q=11和非折疊條件下的性能重構仿真如圖4所示。

(a)折疊條件下的MWC性能重構仿真

(b)非折疊條件下的MWC性能重構仿真

圖4(a)為折疊條件下的MWC性能重構仿真，圖4(b)為非折疊條件下的MWC性能重構仿真。折疊條件下，當信號恢復概率達到90%時，所需信噪比至少要大于-12 dB；非折疊條件下，當MWC系統通道數目為40時，信噪比對信號恢復成功率的影響表明，在信噪比達到-12 dB以上時，信號恢復概率為90%以上。由此表明，MWC系統在折疊和非折疊的條件下，性能重構效果達到90%以上時，所需的信噪比均為-12 dB。

MWC系統在折疊和非折疊條件下的采樣通道數目與信噪比的關系如圖5所示。

(a)折疊條件下采樣通道數目與信噪比的關系

(b)非折疊條件下采樣通道數目與信噪比的關系

圖5(a)為折疊條件下采樣通道數目與信噪比的關系圖，圖5(b)為非折疊條件下采樣通道數目與信噪比的關系圖。折疊條件下，當達到80%以上的重構效果時，MWC系統通道數目需要大于7，而在系統通道數目低于5的條件下，性能重構概率大約為20%；非折疊條件下的采樣通道數目與信噪比的關系，大致呈負指數函數的形式，當采樣通道數目小于20時，性能重構概率為20%，而在通道數目大于20，且信噪比大于-10 dB時，性能重構概率保持在80%以上。

非折疊條件下，MWC的通道數目對信號恢復成功率和信噪比的影響如圖6所示。

(a)非折疊時MWC的通道數目對信號恢復成功率的影響

(b)非折疊時MWC的通道數目對信噪比的影響

圖6(a)為非折疊時MWC的通道數目對信號恢復成功率的影響，圖6(b)為非折疊時MWC的通道數目對信噪比的影響。非折疊條件下，當MWC系統的通道數目在30以上時，信號恢復概率可以達到90%以上；MWC性能重構仿真過程中，當信號恢復概率達到80%條件時，系統通道數目與信噪比之間的作用關系呈現負指數的形式。圖6(b)表明，隨著系統通道數目的增加，若達到80%的信號恢復概率，所需的信噪比逐漸降低。當信噪比低于-5 dB時，所需的通道數目至少為28。

上述的仿真結果表明，利用確定性矩陣作為測量矩陣時，系統性能的重構效果和隨機矩陣作為測量矩陣時的效果相當。在采用折疊的方式對信號進行壓縮采樣時，系統性能的重構效果上和非折疊條件下性能重構效果非常接近。另外，在此基礎上也減少了采樣通道的數目，節約了存儲和傳輸的空間資源，更加便于硬件的實現。

4 結 語

本文研究了MWC系統的壓縮采樣的過程，分析了常用的隨機測量矩陣和確定性測量矩陣的基本構成方式，分別將隨機矩陣和確定性矩陣作為MWC系統的測量矩陣，對MWC系統的信號性能重構做了對比，同時，也研究了在確定性測量矩陣的基礎上，折疊與非折疊條件下，MWC系統的信號重構性能的對比，以及MWC系統的通道數目對信號重構和信噪比的影響。研究結果表明，確定性測量矩陣的重構性能非常接近于隨機測量矩陣的重構性能，折疊條件下的MWC系統的重構性能也非常接近于非折疊條件下的系統的重構性能。通過仿真對比分析，兼顧硬件實現的因素，可以采用確定性的測量矩陣在折疊的方式下，對寬帶信號進行處理來獲取有效的信息。

[1] Mishali M,Eldar Y C. Blind Multi-Band Signal Reconstruction: Compressed Sensing for Analog Signals[J]. IEEE Trans. on Signal Processing, March 2009, 57(30):993-1009.

[2] 王薊翔，張揚.基于矩陣分解的壓縮感知算法研究[J].通信技術，2011，44(16)：138-140. WANG Ji-xiang，ZHANG Yang. Compressed Sensing Algorithm based on Matrix Decomposition[J]. Communications Technology，2011，44(16)：138-140.

[3] Mishali M,Eldar Y C,Dounaevsky O. Xampling: Analog to Digital at Sub-Nyquist Rates[J]. IET Circuits, Devices and Systems, 2011, 5:8-20.

[4] Kirolos S, Laska J,Wakin M. Analog-to-Information Conversion via Random Demodulation[C]. In Proceedings of the IEEE Dallas Circuits and Systems Workshop. Richardson, USA: IEEE, 2006:71-74.

[5] Boufounos P, Baraniuk R G. Sigma Delta Quantization for Compressive Sensing[C].Conference on Wavelets XII, 6701:70104-70104, 2007.

[6] Raz G M. Method and System for Nonlinear and Affine Signal Processing. U. S. Patent 7 173 555, 2007.

[7] Kong X, Petre P, Matic R, et al. An Analog-to Information Converter for Wideband Signals using a Time Encoding Machine[C]. In Digital Signal Processing Workshop and IEEE Signal Processing Educational Workshop, 2011:414-419.

[8] Mishali M,Eldar Y C. From Theory to Practice: Sub-Nyquist Sampling of Sparse Wideband Analog Signals[J]. IEEE Journal of Selected Topics on Signal Processing, Apr. 2010, 4:375-391.

[9] GAN Lu,WANG Hua-li. Deterministic Binary Sequences for Modulated Wideband Converter[C]. SAMPTA2013, Bremen German, 2013:264-267.

[10] ZHENG Shi-lian,YANG Xiao-niu. Wideband Spectrum Sensing in Modulated Wideband Converter based Cognitive Radio System[C]. Communications and Information Technologies (ISCIT), 2011 11th International Symposium on, 2011:114-119.

[11] 李浩. 用于壓縮感知的確定性測量矩陣研究[M]. 北京：北京交通大學. 2011. LI Hao.Research of Determinate Measurement Matrix Utilized in Compressed Sensing[M]. Beijing：Beijing Jiaotong University,2001.

[12] 李小波. 基于壓縮感知的測量矩陣的研究[M]. 北京：北京交通大學. 2010. LI Xiao-bo. Research of Measurement Matrix based on the Compressed Sensing[M].Beijing：Beijing Jiaotong University.2010.

[13] CHEN La-ming,JIN Jian,GU Yuan-tao. A Calibration System and Perturbation Analysis for the Modulated Wideband Converter[C]. Signal Processing (ICSP), 2010 IEEE 10th International Conference on,2010:78-81.

[14] Mishali M,Eldar Y C. Expected RIP:Conditioning of the Modulated Wideband Converter[J]. In Proc. Of IEEE Transactions on Signal Processing, 2009, 57:993-1009.

Broadband Compressive Sampling with Deterministic Measurement Matrix

WANG Xue-ling1, WANG Hua-li1, ZENG Xian-hua1, GUO Ke-feng1, SUN Jiu-hao2

(1.College of Communication Engineering, PLA University of Science and Technology, Nanjing Jiangsu 210007,China; 2.PLA Unit 65040 in Shenyang Tiexi District, Shenyang Liaoning 110005,China)

In the processing of broad signal, the theory of compressed sensing is usually used to acquire effective information. However,of among the compressive sampling structures in practicing this theory, the sampling structure for modulated wideband converter is more suitable to processing broadband signal. The compressive sampling principle of modulated wideband converter is described in this paper, random measurement matrix and determinate measurement matrix also discussed in this paper. With random matrix and deterministic matrix respectively as the measurement matrix of this structure, the reconstruction performances of these two matrixes are compared and analyzed,and based on deterministic measurement matrix, the reconstruction performances in folded and unfolded conditions technically explored. Meanwhile,the influence of channel numbers on the performance reconstruction and signal-to-noise ratio is also analyzed.

compressive sampling; broadband signal; modulated wideband converter; compressed sensing; measurement matrix

10.3969/j.issn.1002-0802.2015.10.003

2015-05-01；

2015-08-19 Received date:2015-05-01；Revised date：2015-08-19

國家自然科學基金(No.61271354)

Foundation Item:National Natural Science Foundation of China (No.61271354)

TN911

A

1002-0802(2015)10-1111-05

王學玲(1989—)，女，碩士，主要研究方向為壓縮感知與信號處理技術；

王華力(1967—)，男，博士，教授，主要研究方向為信息感知與信號處理；

曾顯華(1990—)，男，碩士，主要研究方向為壓縮感知與信號處理技術；

郭克鋒(1990—)，男，博士，主要研究方向為協同通信傳輸技術；

孫久皓(1988—)，男，學士，主要研究方向為一體化指揮專網。