Compton散射對激光等離子體通道天線特性的影響

禹定臣， 郝東山

(1.黃淮學院信息工程學院， 駐馬店 463000； 2.鄭州工業應用技術學院信息工程學院， 新鄭 451150)

Compton散射對激光等離子體通道天線特性的影響

禹定臣1， 郝東山2

(1.黃淮學院信息工程學院， 駐馬店 463000； 2.鄭州工業應用技術學院信息工程學院， 新鄭 451150)

應用多光子非線性Compton散射模型和數值計算方法，研究了激光等離子體通道天線傳播和輻射特性，結果表明：隨通道周圍介質損耗和傳輸模式階數的增大，傳輸模式THnm衰減常數明顯增大.這是因散射使通道內外電場和磁場增強，粒子間碰撞頻率增大，電場使更多分子電離而吸收更多能量的緣故.隨模式階數增大，電性有耗介質使相移常數明顯減小.這是因散射使高階模式可能存在被耦合電場俘獲的緣故.等離子體耦合頻率為0.7附近，衰減常數隨頻率增大而劇烈增大.這是因散射使介質分子發生二、三階電離，更多電子被耦合電場急劇加速的緣故.隨天線長度增加，天線輻射方向圖主瓣和副瓣數量、寬度和最大輻射方向發生明顯變化.這是因散射使天線頻率增大，輻射波長變短，粒子電離幾率增大，輻射波能量和頻率成分增大的緣故.

激光等離子體通道天線； 傳輸模式； 輻射特性； 耦合； 多光子非線性Compton散射

1 引 言

因大功率等離子體天線有重要應用，如大功率微波武器[1]、隱身技術[2]、核聚變快點火[3]等，故引起了人們的關注[4-7].Caillault等[8]設計出平面等離子體反射天線結構.Donald等[9]給出了該天線反射電磁波噪聲產生機制.鑒福升等[10]指出，等離子體碰撞頻率是影響反射波的主要因素.胡強林等[11]指出，圓和線極化行波輻射阻尼效應隨等離子體密度增大而增大，高激光脈沖重復率頻率可提高輻射阻尼效應[12].Petrova等[13]指出，注入不同條件激光可使通道壽命延長，不同線型脈沖對壽命影響較大[14].楊利霞等[15]提出新的電流密度拉普拉斯變換時域有限差分法計算等離子體球輻射.大多研究基于玻璃管封裝惰性氣體產生等離子體，使大功率等離子體天線增益受限[16,17].如何尋求大功率等離子體天線已成為亟待解決的重要課題.近期，夏新仁等[18]提出新概念激光等離子體通道天線構想.應指出的是，以上對等離子體通道天線研究均未考慮非線性Compton散射.文樺等[19]指出，等離子體內波強達1016W/cm2量級，非線性Compton散射開始顯現.可見，Compton散射對等離子體天線輻射影響不可忽略.本文正是對該問題進行了研究.

2 天線設計及工作原理

等離子體通道天線的設計原理圖如圖1所示，其工作原理是：激光器發出的超強激光使空氣電離且發生多光子非線性Compton散射，入射光和Compton散射光形成耦合等離子體通道，同步信號脈沖器的脈沖通過天線耦合到等離子體通道內，脈沖和通道以接近光速的速度同步向前傳輸，通過通道的側面向外輻射電磁波.

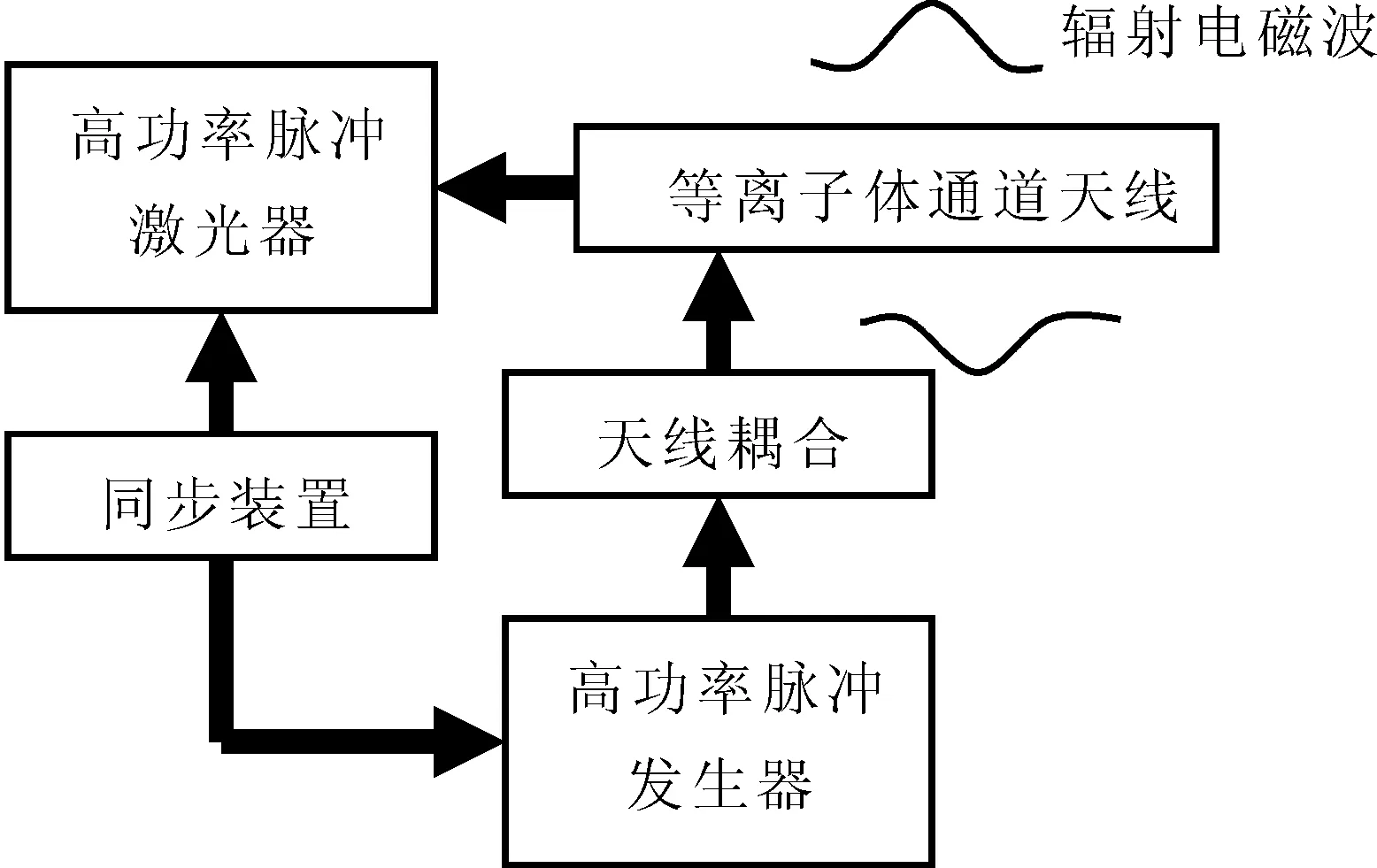
圖1 等離子體通道天線示意圖Fig.1 Sketch map of plasma channel antenna

3 天線傳播特性

因由通道導行傳輸的電磁波始終滯后激光脈沖極短時間，且通道可近似為半徑恒定、密度均勻的等離子體圓柱，故可將天線等效為周圍充滿有耗氣體的無限長圓柱體，其模型如圖2所示.

圖2 等離子體通道天線電磁模型Fig.2 Electromagnetic model of plasma channel antenna

若等離子體中發生非線性Compton散射(簡稱散射)，入射與散射光形成的耦合光頻為[6]

(1)

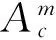
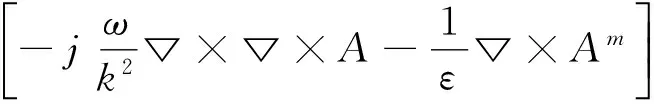
(2)

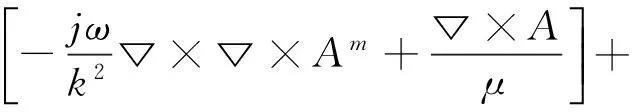
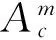
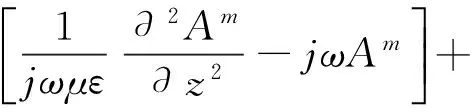
(4)

(5)

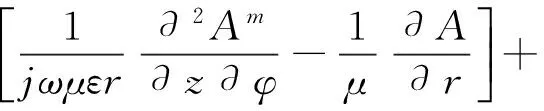
(6)

通道內外耦合矢量位可分別表示為

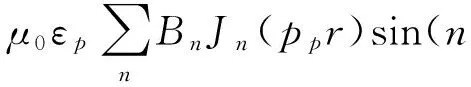
exp(-jkz)+(Δωμ0εp+ωμ0Δεp+ωμ0εp)

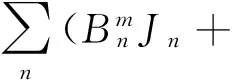
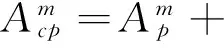
exp(-jkz)，r≤a

(7)

exp(-jkz)+j(ΔωμLεL+ωΔμL+ωμLΔεL)

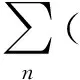
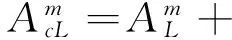
exp(-jkz)+j(ΔωμLεL+ωΔμL+ωμLΔεL)

(8)

ΔxpJnBn+

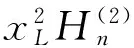
(9)

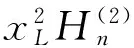
(10)

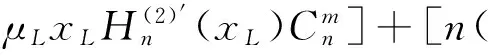
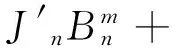
(11)

(12)

其中xp=ppa，Δxp=Δppa；xL=pLa，ΔxL=ΔpLa.由式(9)～(12)非零解條件，可得

(ΔμrH+μrΔH)](J-εLpH)-(J-μtH)[ΔJ-

(13)

取通道周圍有耗介質的電和磁性參數分別為Reεcr=5.5和μcr=1及Reμcr=5.5和εcr=1、ωcpe/ω=0.5、a/λ=6時，通道內THnm衰減和相移常數隨介質損耗變化如圖3～5所示.由圖3～5知，衰減隨通道周圍介質損耗和傳輸模式階數增大明顯增大，同階模式下，前者遠大于后者.這是因散射使電和磁場增強，碰撞頻率增大使更多電離分子吸收更多能量的緣故.同階模式下，前者對相移影響大于后者，隨模式階數增大，相移常數明顯減小.這是因散射使高階模式被電場俘獲的緣故.

圖3 電性有耗介質下傳輸模式衰減常數隨介質損耗的變化Fig.3 Changes on attenuation constant of propagation model along dielectric loss under electric dielectric

圖4 磁性有耗介質下傳輸模式衰減常數隨介質損耗的變化Fig.4 Changes on attenuation constant of propagation model along dielectric loss under magnetism dielectric

圖5 傳輸模式相移常數隨周圍介質介質損耗的變化Fig.5 Changes on phase moving constant of propagation model along near dielectric loss

取等離子體通道周圍的電性和磁性介質的參數分別為εcr=5.66(1-j)和μcr=1及μcr=5.66-5.66j和εcr=1、a/λ=6，THnm的衰減常數和相移常數隨著ωcp/ω的變化分別如圖6～8所示.由圖6知，同階模式的電性和磁性介質對相移常數的影響幾乎是相等的，隨著模式階數的增大，該常數發生了微小的減小.這是因為散射使電子的輻射阻尼增強效應導致高階模式吸收的能量減小，其被電場俘獲效應消失的緣故.由圖7和8知，ωcp/ω=0.7附近，衰減常數隨著ωcp/ω的增大而劇烈地增大.這是因為散射使分子發生了二階和三階電離，有更多的電子被電場急劇加速的緣故.

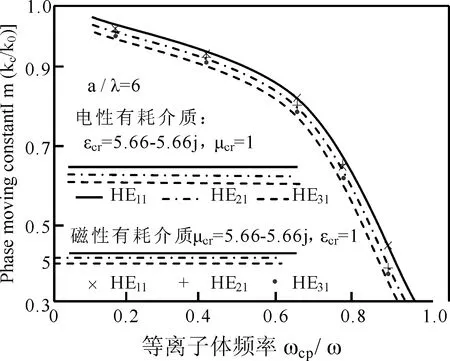
圖6 傳輸模式相移常數隨等離子體頻率的變化Fig.6 Changes on phase moving constant of propagation model along plasma frequency

圖7 通道周圍為電性有耗氣體介質時，傳輸模式衰減常數隨等離子體頻率的變化Fig.7 Changes on attenuation constant of propagation model along plasma frequency dielectric loss under electric dielectric near channel

圖8 通道周圍磁性為有耗氣體介質，模式衰減常數隨等離子體頻率的變化Fig.8 Changes on model attenuation constant along plasma frequency under magnetism dielectric near channel

4 天線輻射特性

將激光等離子體通道天線等效為周圍充滿空氣、密度均勻、半徑和長度為a和L的如圖9和10所示等離子體圓柱體，分別為從天線初始端耦合電磁波的單極式天線和從通道中間耦合電磁波的駐波對稱振子式天線.

圖9 單極式等離子體通道天線示意圖Fig.9 Sketch map of channel antenna of single polar laser plasma

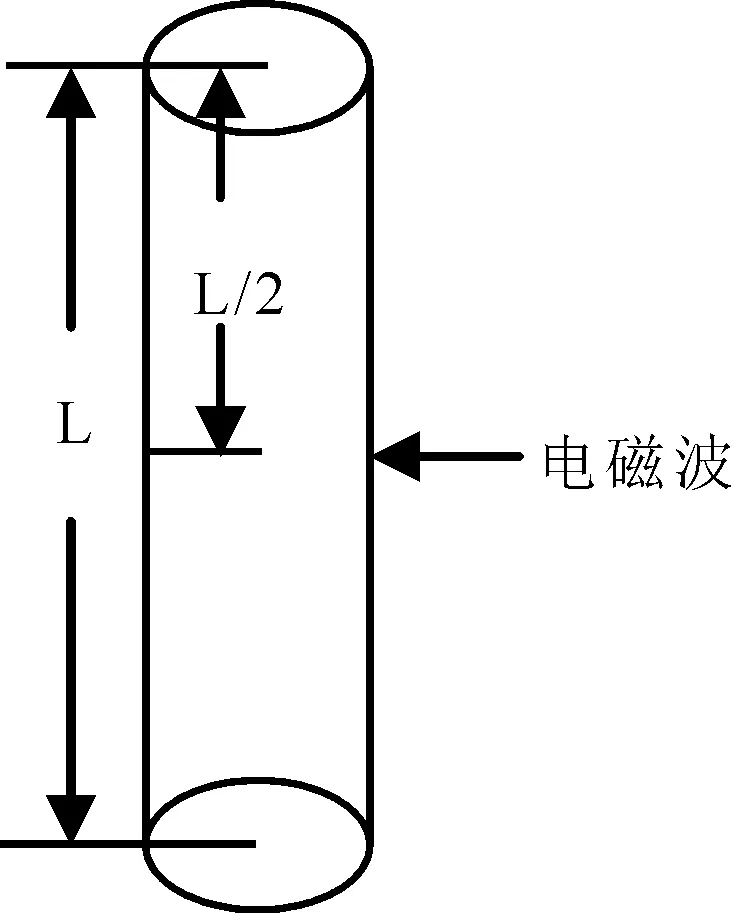
圖10 駐波對稱振子式等離子體通道天線示意圖Fig.10 Sketch map of channel antenna of laser plasma of standing wave symmetry oscillation

圖9天線，信號在通道表面以行波傳輸且與等離子體發生散射時，其表面耦合電流為

′)+ΔJx(Δz′)≈

J0exp[j(ωt-kz′)]+ΔJ0exp[j(ωt-kz′)]

(14)

式中，ω為信號頻率；J0和ΔJ0分別為散射前的電流振幅及其擾動.對于較短的天線，輻射電場方向函數為

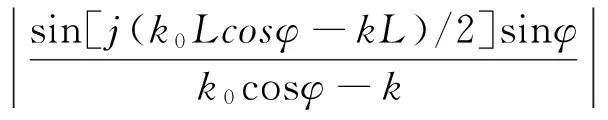
(15)

對圖10天線，其表面耦合電流為

(16)

由式(15)和(16)，可得

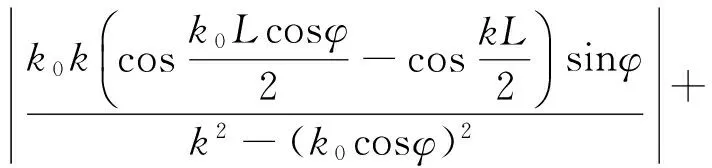
(17)

取εcr=μcr=1，結合輻射場對稱性及其主模式為n=0的TM表面波，得TM波在天線周圍空氣中的縱和橫向電磁場在圓柱坐標系中的關系為

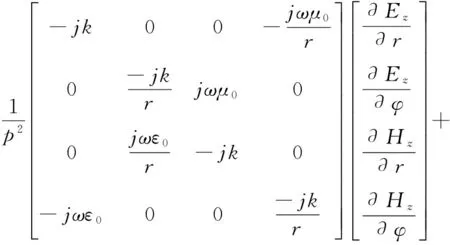
(18)

由式(18)，可得橫向電磁場切向分量及橫向電磁場分別為

(19)

Ecφ=0

(20)

Ecpz=Ac1J0(ppr)exp(-jkz)+

Ac1ΔJ0(Δppr)exp(-jkz)

(21)

Hcpz=0

(22)

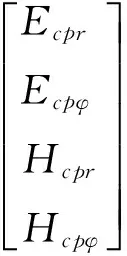
(23)

橫向電磁場的切向分量為

(24)

Ecpφ=0

(25)

對單極天線取ωcp=31.4 GHz,νcp=4 GHz,a=2 mm,ω=500 MHz，L=λ/4、λ/2、λ時，E面輻射方向和f(φc)隨φc=φ+Δφ變化如圖10和11所示.由圖10知，0

圖11 單極式天線的fcΦ隨Φ的變化Fig.11 Changes on f cΦ of single polar antenna

對于稱振子式天線取圖10和11中的參數，E面輻射方向隨著天線長度的變化關系如圖12所示.由圖12知，當0

圖12 對稱振子式天線方向圖隨天線長度的變化Fig.12 Changes on direction map of symmetry oscillation along antenna length

圖13 對稱振子式天線方向圖隨等離子體密度的變化Fig.13 Changes on direction map of symmetry oscillation along plasma density

圖14 對稱振子式天線方向圖隨通道半徑的變化Fig.14 Changes on direction map of symmetry oscillation along channel radius

5 結 論

本文基于多光子非線性Compton散射模型，分析了散射對天線特性的影響，得出如下結論：

1)與散射前相比，隨通道周圍介質損耗和模式階數增大，模式衰減常數明顯增大.電性有耗介質使較高階模式相移常數明顯減小.隨同階模式階數增大，兩介質對相移常數影響幾乎相等.

2)等離子體耦合頻率ωcp/ω=0.7附近, 衰減常數隨耦合頻率增大而急劇增大.

3)隨單極式天線長度增加, 其輻射方向圖主瓣寬明顯減小, 最大輻射方向由180°向90°方向明顯移動，主瓣和第一副瓣方向系數均明顯增大.對稱振子式天線長度0

4)隨電子密度增大, 輻射方向主瓣由2瓣變為1瓣, 最大輻射方向由0°和180°方向轉向90°方向, 主瓣明顯變寬.

5)隨等離子體通道半徑增大, 輻射方向主瓣由2瓣變為1瓣, 最大輻射方向由0°和180°方向轉向90°方向, 主瓣更寬.

對以上結論給出了初步物理解釋.這些結論對于人們設計和控制等離子體通道天線傳輸特性應具有一定的參考價值.

[1] Ginzburg N S, Korovin S D, Pegel I V,etal. Production of ultra-short high-power microwave pulses in Cerenkov backward-wave systems [J].LaserPhysics, 2006, 16(1): 79.

[2] Chen L S, Ma H X. Applying in aerial stealthy on plasma technology [J].RadarScienceandTechnology, 2005, 3(3): 375(in Chinese)[ 陳林松, 馬紅星. 等離子體技術在天線隱身中的應用[J]. 雷達科學與技術, 2005, 3(3): 375 ]

[3] Song Z X, He L M, Zhang J H,etal. 3D numerical simulation of supersonic plasma ignition process [J].HighPowerLaserandParticleBeams, 2013, 24(11)：1746(in Chinese)[ 宋振興, 何立明, 張建邦, 等. 超音速等離子體點火過程的三維數值模擬[J]. 強激光與粒子束, 2013, 24(11): 1746 ]

[4] Feng G H, Hao D S. A new model on photonic band gap structure in high power laser PPCs under Compton scattering [J].JournalofAtomicandMolecularPhysics, 2012, 29(1): 91(in Chinese)[ 馮光輝, 郝東山. Compton散射下激光PPCs光子帶隙結構新模型[J]. 原子與分子物理學報, 2012, 29(1): 91 ]

[5] Liu J T, Hao D S. Influence of initial velocity of ion on iplasma sheath thickness under Compton scattering [J].JournalofAtomicandMolecularPhysics, 2014, 31(3): 443(in Chinese)[ 劉經天, 郝東山. Compton散射下離子初始速度對等離子體鞘層厚度的影響[J]. 原子與分子物理學報, 2014, 31(3): 443 ]

[6] Liu A H, Hao X F, Hao D S. Influence of Compton scattering to propagation of oblique laser pulse in plasma [J].JournalofAtomicandMolecularPhysics, 2011, 28 (6): 102(in Chinese)[ 劉安輝, 郝曉飛, 郝東山. Compton散射對斜入射激光脈沖在等離子體中傳輸的影響[J]. 原子與分子物理學報, 2011, 28 (6): 102 ]

[7] Yu D C, Hao X F, Hao D S. Gain clan of cross -phase modulation instability of plasma under Compton scattering [J].JournalofAtomicandMolecularPhysics, 2013, 30(1): 167(in Chinese)[ 禹定臣, 郝曉飛, 郝東山. Compton散射下等離子體交叉相位調制不穩定性增益譜[J]. 原子與分子物理學報, 2013, 30(1): 167 ]

[8] Caillault L, Larigaldie S. Mechanisms of a linear hollow cathode used for the production of a helium plasma sheet [J].J.Phys. D:Appl.Phys., 2002, 35: 1010.

[9] Donald P M, Richard F F, Robert E P,etal. Microwave emission from plasmas produced by magnetically confined electron beams [J].IEEETrans.PlasmaSci., 2002, 32 (2): 426.

[10] Jian F S, Zeng H, Zou H Y. Simulation of plasma planar reflecting electromagnetic wave [J].ShipElectronicEngineering, 2011, 31 (4): 102(in Chinese)[ 鑒福升, 曾浩, 鄒勇華. 等離子體平面反射電磁波的模擬仿真[J]. 艦船電子工程, 2011, 31(4): 102]

[11] Hu Q L, Xiao G L, Yu X G. Radiation damping effects in ultra-intense laser-plasma interaction [J].HighPowerLaserandParticleBeams, 2013, 25 (6): 1379(in Chinese)[ 胡強林, 肖桂蘭, 余曉光. 強激光-等離子體相互作用過程中的輻射阻尼效應[J]. 強激光與粒子束, 2013, 25 (6): 1379 ]

[12] Chen J Z, Bai J N, Song G J,etal. Effects of laser shot frequency on plasma radiation characteristics [J].SpectroscopyandSpectralAnalysis, 2012, 32 (11): 2916(in Chinese)[ 陳金忠, 白津寧, 宋廣聚, 等. 激光脈沖重復率對等離子體輻射特性的影響[J]. 光譜學與光譜分析, 2012, 32(11): 2916 ]

[13] Petrova T B, Ladouceur H D, Baronavski A P. Numercial modeling of the electrical breakdown and discharge properties of laser-generated plasma channels [J].Phys.Rev. E, 2007, 76: 066.

[14] Wang H T, Fan C Y, Shen H,etal. Temporal evolution of plasma density in femto-second light filaments [J].HighPowerLaserandParticleBeams, 2012, 24 (5): 1024(in Chinese)[ 王海濤, 范承玉, 沈紅, 等. 飛秒光絲中等離子體密度時間演化特征[J]. 強激光與粒子束, 2012, 24(5): 1024 ]

[15] Yang L X, Shen D H, Shi W D. Analyses of electromagnetic scattering characteristics for 3D time-varying plasma medium [J].ActaPhy.Sin., 2013, 62 (10): 104101(in Chinese)[ 楊利霞, 沈丹華, 施衛東. 三維時變等離子體目標的電磁散射特性研究[J]. 物理學報, 2013, 62(10): 104101 ]

[16] Lu X.Researchonhighpowermicrowavepulseintheairbreakdown[C].6th International Symposium on Anten-nas, Propagation and EM Theory Proceedings, Beijing, 2003, 537.

[17] Yang J H, Niu Z X, Zhou D F,etal.Thetemporaldispersecharacterinthenonlinearpropagationofhighpowermicrowave[C]. Asia-Pacific Radio Science Conference, Qingdao, 2004, 459.

[18] Xia X R, Wang S J, Jin X L,etal. Theoretical study on new conception laser plasma channel antenna [J].JournalofCAEIT, 2011, 6(2): 147(in Chinese)[ 夏新仁, 王守杰, 金賢龍, 等. 新概念激光等離子體通道天線的研究[J]. 中國電子科學研究院學報, 2011, 6(2): 147 ]

[19] Wen H, Hao X F, Hao D S. Influences of Compton scattering on transverse dispersion of relativistic electron-positron plasma [J].LaserandOptoelectronicsProgress, 2012, 49(8): 081902(in Chinese)[ 文樺, 郝曉飛, 郝東山. Compton散射下等離子體初溫對質子產生的影響[J]. 激光與光電子學進展, 2012, 49(8): 081902 ]

Influences of Compton scattering on the properties of laser plasma channel antenna

YU Ding-Chen， HAO Dong-Shan

( 1. College of Information Engineering， Huanghuai University， Zhumadian 463000, China； 2. College of Information Engineering， Zhengzhou University of Industrial Technology， Xinzheng 451150, China )

By using the model of multi-photon nonlinear Compton scattering and the numerical computing means， the properties of the propagation and radiation of laser plasma channel antenna are studied. The results show that the attenuation constant of the propagation model THnmis clearly increased along the increases of the dielectric loss near the channel and the propagation model step number. The causes are that the electric field and magnetic field in and outside the channel are increased by Compton scattering， the collision frequency between the particle and particle is increased， and even more energies are absorbed by the even molecules ionized by Compton scattering. The phase moving constant is clearly decreased by the electric loss dielectric along the increasing model step number. This is dus to the possibility on the capture of the high step model by the coupling electric field. Near 0.7 coupling plasma frequency， the attenuation constant is acutely increased along the increasing frequency. The cause are that the 2nd and 3rd step ionizations of the medium molecule are taken by Compton scattering， and the even more electrons are sharply accelerated by the coupling electric field. The numbers of the main and vice piece， the widths and the maximum radiation directions in the map of the antenna radiation direction are clearly changed along the increasing antenna length. The cause are that because of the scattering，the antenna frequency is creased， the radiation wave length is decreased， the probability particle ionization is increased， and the energy and radiation wave frequency composition are increased.

Laser plasma channel antenna； Propagation model； Radiation characteristic； Coupling； Multi-photon nonlinear Compton scattering

2014-09-04

河南省基礎與前沿技術資助項目(092300410227)

禹定臣(1970—), 男，副教授，碩士，主要從事信號傳輸技術研究.

郝東山.E-mail: haodongshan@126.com

103969/j.issn.1000-0364.2015.10.016

TN011

A

1000-0364(2015)05-0815-08