PS(X2Πr)基態勢能函數與光譜常數研究

蔡昌梅, 趙 俊

(長江大學物理科學與技術學院, 荊州 434023)

PS(X2Πr)基態勢能函數與光譜常數研究

蔡昌梅, 趙 俊

(長江大學物理科學與技術學院, 荊州 434023)

根據群論及原子分子反應靜力學的有關原理,推導了PS基態分子電子態及其合理的離解極限.采用Gaussian 03 軟件中的密度泛函理論B3LYP和B3P86結合6-311++G (3df,3pd)、6-311++G、6-311G(3df, 3pd)、cc-pVTZ和D95基組,對PS分子基態平衡結構和諧振頻率進行了計算.通過比較計算結果,發現B3P86方法結合cc-pVTZ 基組計算所得結果與實驗值最接近.在該水平下對PS分子的基態進行了單點勢能掃描計算,利用正規方程組擬合三參數的Murrell-Sorbie函數和修正的Murrell-Sorbie+C6函數,得到了基態PS分子完整的勢能函數與相應的光譜常數ωe、ωexe、Be和αe的值.計算結果表明,利用三參數的Murrell-Sorbie函數計算所得的光譜常數與實驗數據吻合得更好.

基態PS； 分子結構； 勢能函數； 光譜常數

1 前 言

勢能函數不僅是分子本身的幾何結構與電子結構的完全描述[1,2],也是核運動的有效描述,同時它又是研究分子反應動力學的關鍵[3-5].勢能函數的提出和不斷的更改經歷了漫長的時間,Murrell和sorbiel[6]等人提出擴展的Rydberg勢能函數,也被稱為Murrell-Sorbie(M-S)函數.最近,有課題組報道了采用修正的Murrel-Sorbie+c6(M-S+ c6)函數進行研究并取得了較滿意的計算結果的研究工作[7].M-S函數和修正的M-S+c6函數是研究基態雙原子分子很好的勢能函數形式,它不僅廣泛應用于單價離子,而且也適用于電中性雙原子分子.

1955 年,Dressler及其合作者[8,9]最早發現PS自由基的電子光譜；1969 年,Narasimham 和Subramanian[10,11]等人證實了該譜線的存在并得到PS 自由基光譜；1977 年, Jenouvrier 和Pascat[12]首次報道了PS自由基的諧振頻率和非諧振頻率等光譜常數；1979 年,Balasubramanian 等人[13]得到了PS 自由基在各種紫外線波段的光學性質；同年,Huber 和 Herzberg[14]報道了實驗測定的PS 自由基的一些光譜常數；2012年,朱家偉[15]等對PS、PS+和 PS-的勢能曲線進行了能量掃描.雖然前期的理論和實驗研究工作得到了一些有意義的結論,但是采用M-S勢能函數以及修正過的M-S+c6勢能函數擬合PS基態分子勢能函數的研究工作尚未見報道,因此,我們有必要來進一步研究基態PS分子的精確勢能函數.

2 PS分子基態的離解極限

PS分子為異核雙原子直線型分子,屬于C∞v群.要想獲得其正確的勢能函數,需要合理的確定其離解極限.根據原子分子反應靜力學原理包含的四個基本要點Wigner-Witmer規則、微觀過程的可逆性原則、微觀過程的傳遞性原則和最優能量過程原則可以構造出上述分子可能的電子態.查表可知P原子基態電子態為4Su、2Du和2Pu,S原子基態電子態為3Pg,具體如表1所示.

由微觀過程的可逆性原理以及最優能量過程規則[16],P、S兩原子基態電子態的能量最低,可知PS分子基態X2Πr的合理離解極限為：

PS (X2Πr)→P(4Su) +S(3Pg)

(1)

3 計算結果與討論

3.1 方法和基組的優選

運用Gaussian03程序進行分子的相關能量計算時,采用不同的方法和基組將直接影響結果的可靠性,所以為了得到更為精確的結果,本文運用兩種密度泛函理論B3LYP和B3P86結合五種基組6-311++G、6-311++G(3df,3pd)、6-311G(3df,3pd)、cc-pVTZ和D95進行優化計算,并將計算結果與實驗值進行比較.優化計算的PS分子基態X2Πr的平衡核間距Re、諧振頻率ωe以及離解能De,所得結果如表2所示.

比較表2中各方法的計算值與實驗值,發現B3LYP/6-311++G和B3P86/cc-pVTZ的結果較為精確,結合能量最低原則,選取B3P86/cc-pVTZ方法進行下面的計算工作.

3.2 PS分子基態(X2Πr)的解析勢能函數與光譜常數的計算

在完成了幾何結構優化后,結合實驗值與相關理論選出的B3P86/CC-PVTZ水平上,對PS分子基態(X2Πr)進行單點能掃描計算.在掃描計算的過程中使用的各種參數,變化只有P原子與S原子的核間距離r,其它參數都與結構優化時保持嚴格一致,得到PS分子基態(X2Πr)一系列單點能掃描值,結果如表3所示.

在單點掃描的基礎上,分別用M-S函數和修正后的M-S+c6函數進行最小二乘擬合得到基態PS分子的勢能函數：

M-S函數：

V= -De(1 +a1ρ+a2ρ2+a3ρ3)exp(-a1ρ)

(2)

表1 P、S基態和激發態電子態的直積

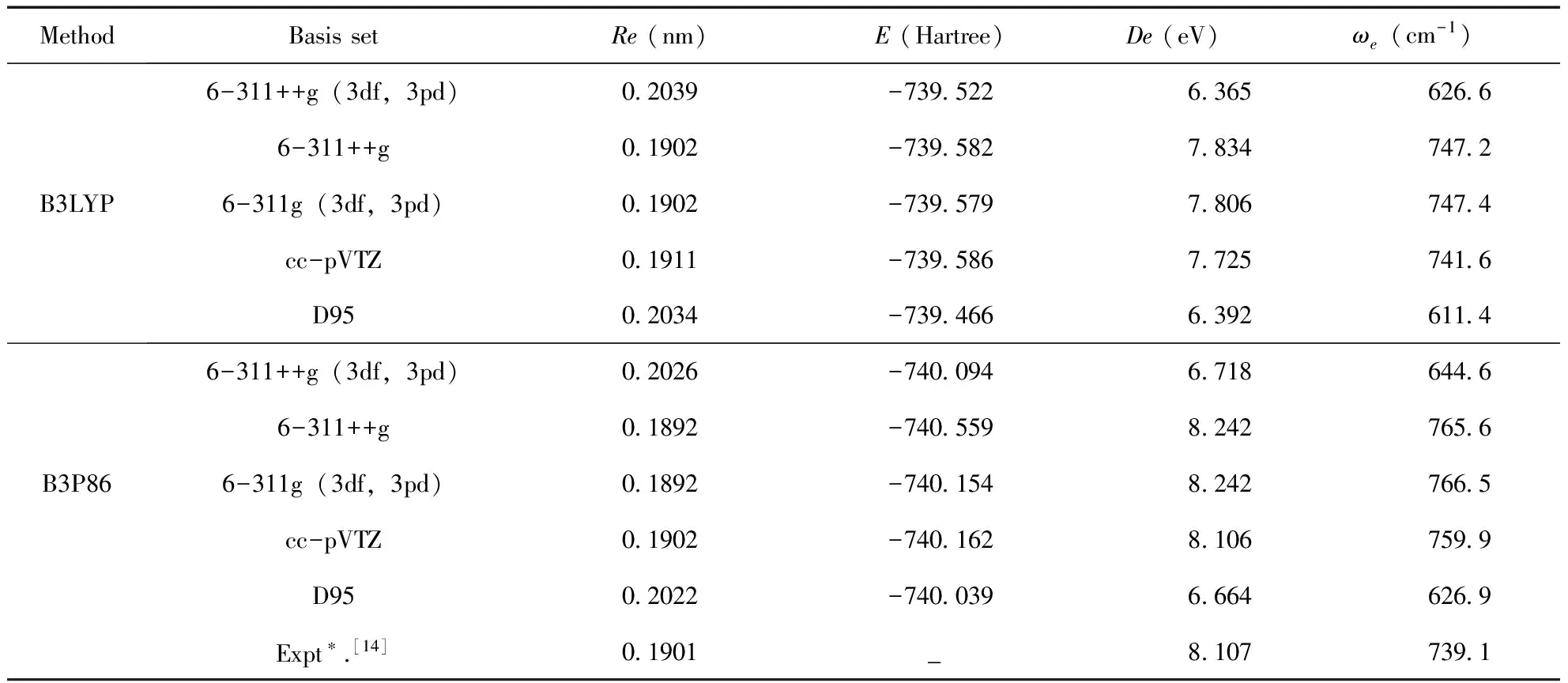
表2 PS分子基態(X2Πr)的優化計算結果

修正后的M-S+c6函數：

V= -De(1 +a1ρ+a2ρ2+a3ρ3)

exp(-a1ρ) -c6/R6

(3)

兩個式子中,ρ=R-Re,R為核間距,Re為平衡核間距,a1,a2,a3及c6為擬合參數.

勢能曲線的函數擬合范圍是 0.05-0.645 nm,步長取為 0.005 nm,一共120個點,在此范圍內擬合勢能函數完全收斂.擬合的勢能曲線圖如圖1、圖2所示,其中圖1是用M-S函數擬合PS分子基態(X2Πr)所得的勢能曲線,圖2是用修正后的M-S+c6函數擬合PS分子基態(X2Πr)所得的勢能曲線.兩個圖中圓圈均代表單點能掃描所得到的點,屬于計算值,曲線代表計算結果經過勢能函數擬合后的勢能函數曲線.觀察兩幅圖,我們很容易發現,兩幅圖中單點能掃描得到的點都很好的與經過函數擬合后的曲線重合,圖1中用M-S勢能函數擬合得到的勢能曲線擬合關聯度為0.99977,圖2中用修正的M-S+c6勢能函數擬合得到勢能曲線的擬合關聯度為0.99981.擬合參數見表4.

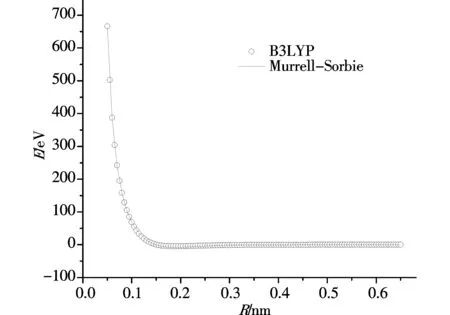
圖 1 用M-S函數擬合PS分子基態(X2Πr)所得的勢能曲線Fig.1 The potential energy curve of PS (X2Πr) fitted by M-S potential function

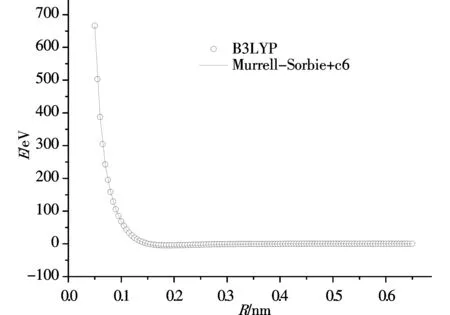
圖 2 用修正后的M-S+c6函數擬合PS分子基態(X2Πr)所得的勢能曲線Fig.2 The potential energy curve of PS (X2Πr) fitted by modified M-S+c6 potential function

雖然經過修正M-S+c6勢能函數擬合的擬合關聯度較高,但是由表4可以看出經過修正M-S+c6勢能函數擬合后,相關的擬合參數與實驗值相差更大.所以我們可以得到由標準的3參數M-S勢能函數擬合結果更好.由勢能函數與各階力常數的關系

(4)

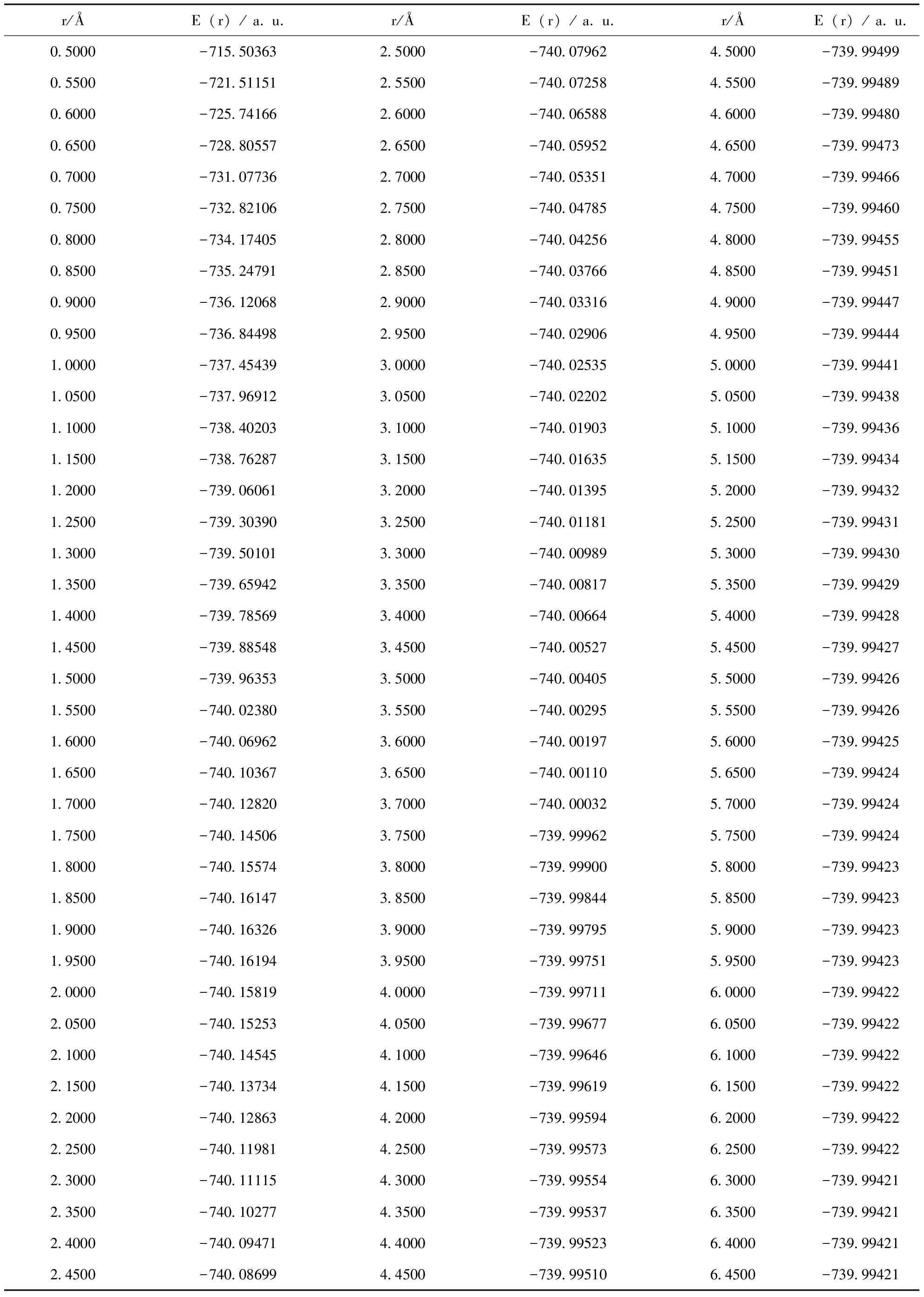
表3 B3P86/cc-pvtz理論方法下PS分子基態(X2Πr)

表4 PS分子基態(X2Πr)的M-S和M-S+c6勢能函數參數

表5 PS分子基態(X2Πr)的各階力常數

表6 PS分子基態(X2Πr)的光譜常數

和得到的勢能參數值,我們可以計算出二階f2、三階f3和四階f4力常數.由M-S函數我們可以推導出的f2、f3和f4的表達式分別為：

(5)

(6)

(7)

由修正的M-C+c6函數推導出的f2、f3和f4的表達式分別為：

(8)

336 c6/ Re9

(9)

3024 c6/ Re10

(10)

由表4中各勢能函數的擬合參數,則可以計算出PS分子的二階f2、和三階f3及四階f4力常數,計算結果列于表5中.

在得到如上各階力常數后,我們可以根據力常數與光譜常數的關系[17],運用下列公式可計算出PS分子基態(X2Πr)的光譜常數Be,ωe,αe,ωexe,

(11)

(12)

(13)

(14)

式中,Be為剛性轉動因子,ωe為諧振頻率,αe為非剛性轉動因子,ωexe為非諧振頻率,μ為分子的約化質量,c為光速,經過計算后得到的結果如表6所示.

4 結 論

采用Gassian03程序包中B3LYP和B3P86方法,結合6-311++G (3df, 3pd)、6-311++G、6-311g(3df, 3pd)、cc-pVTZ和D95基組對PS分子基態(X2Πr)進行了結構優化計算.通過與實驗值比較,優選出B3P86/cc-pVTZ方法為最合理的計算PS分子基態(X2Πr)勢能函數的方法.分別采用標準的M-S勢能函數和M-S+c6勢能函數進行最小二乘擬合,并得到了相應的光譜常數.通過與實驗值比較,用標準M-S勢能函數擬合后得到的光譜數據更靠近實驗值,這說明標準的M-S勢能函數能更精確地描述PS分子基態(X2Πr)的結構特征和能量變化.本文所得數據可用于進一步研究PS分子基態反應動力學過程,也為PS分子基態的實驗和理論研究提供了可靠的理論參考.

[1] Xie A D, Zhu Z H. Potential energy functions for the electronic states X1Σ+, A1P and B1Σ+of molecule BF [J].ActaChim.Sinica, 2005, 6: 2126(in Chinese)[謝安東, 朱正和. BF分子X1Σ+、A1P和B1Σ+態的勢能函數[J]. 化學學報, 2005, 63： 2126]

[2] Liu F L, Zhao Y F, Li X Y,etal. Density function study of potential energy function and stability of MT1(M=Cu,Au,Ag)[J].ActaChim.Sinica, 2006, 64: 157 (in Chinese) [劉鳳麗, 趙永芳, 李新營, 等．MT1(M=Cu,Au,Ag)分子的勢能函數與穩定性的密度泛函研究[J]. 化學學報, 2006, 64： 2157]

[3] Huang D H, Wang P H, Zhu Z H. Study of potential function for ground state N2O-[J].ActaChim.Sinica, 2007, 65: 994 (in Chinese) [黃多輝, 王藩侯, 朱正和． 基態N2O-的勢能函數研究[J]． 化學學報, 2007, 65： 994]

[4] Ni Y, Jiang G, Zhu Z H,etal. Structures and potential energy functions of PdYH molecule[J].ActaChim.Sinica, 2005, 63: 764 (in Chinese) [倪羽, 蔣剛, 朱正和, 等. PdYH分子的結構域勢能函數[J]．化學學報, 2005, 63： 64][5 ] Li Q, Wang H Y, Jiang G,etal. Potential energy function and stability of RuX2+(X=O, H,N, C) [J].ActaChim.Sinica, 2001, 59: 1376 (in Chinese) [李權, 王紅艷, 蔣剛, 等. RuX2+(X=O, H, N, C)分子離子的勢能函數與穩定性[J]． 化學學報, 2001, 59： 1376]

[6] Murrell J N, Sorbie K S. New analytic form for potential energy curves of stable diatomic state[J].J.Chem.Soc.FaradayTrans., 1974, 70： 1552．

[7] Xu M, Wang R K, Linghu R F,etal. Structures and potential energy functions of the ground states of BeH, BeD, BeT molecules [J].ActaPhys.Sinica, 2007, 56: 769 (in Chinese) [徐梅, 汪榮凱, 令狐榮鋒, 等. BeH、BeD、BeT分子基態(X2Σ+)的結構與勢能函數[J]. 物理學報, 2007, 56： 69]

[8] Dressler K. Ultraviolett- und schumannspektren der neutralen und ionisierten molekule PO, PS, NS, P2[J].Helv.Phys.Acta, 1955, 28: 563.

[9] Dressler K, Miescher E. Spectroscopic identification of diatomic PS and new band systems of PO and P2[J].Proc.Phys.LondonSoc. A, 1955, 68： 542.

[10] Narasimham N A, BalaSubramanian T K. Isotope shift studies in the spectra of NS and PS [J].J.Mol.Spectrosc., 1969, 29: 294.

[11] Narasimham N A, Balasubramanian T K.The ultra-violet bands of PS [J].J.Mol.Spectrosc., 1971, 37: 371.

[12] Jenouvrier A, Pascat B. Le spectre électronique de PS B2Π-X2Π [J].Can.J.Phys.,Premièrepartie:lesysteme, 1978, 56: 1088.

[13] Balasubramanian T K , Dixit M N, Narasimham N A. Rotational analysis of the ultraviolet bands of PS [J].Pramana, 1979, 12： 707.

[14] Huber K P, Herzberg G.Molecularspectraandmoleculastructure[M]. Vol.4, Constants of Diatomic Molecules, Van Nostrand Reinhold: New York, 1979： 544.

[15] Zhu J W 2012 M.S. Thesis (Henan: Henan Normal University) (in Chinese) [朱家偉. 2012 碩士學位論文 (河南：河南師范大學)]

[16] Zhu Z H.Atomicandmolecularreactionstatics[M]. Beijing: Science Press, 1996： 59 (in Chinese) [朱正和.原子分子反應靜力學[M]. 北京： 科學出版社, 1996： 59]

[17] Zhu Z H, Yu H G.Molecularstructureandmolecularpotentialenergyfunction[M]. Beijing: Science Press, 1997： 99(in Chinese) [朱正和, 俞華根. 分子結構與分子勢能函數[M]. 北京： 科學出版社, 1997： 99]

Study on the analytic potential energy function and spectroscopic constants of the PS molecule

CAI Chang-Mei, ZHAO Jun

(School of Physical Science and Technology, Yangtze University, Jingzhou 434023, China)

The ground electronic state and the reasonable dissociation limit of PS molecular ion have been correctly determined based on group theory and atomic and molecular reaction statics. The energy, equilibrium geometry and harmonic frequency of the ground electronic state of PS molecular ion have been calculated using the B3LPY and B3P86 method with 6-311++G (3df, 3pd), 6-311++G, 6-311G(3df, 3pd), cc-pVTZ and D95 basis sets. The whole potential curves for the ground electronic state are further scanned using the above method, the potential energy functions and relevant spectroscopic constants of this state are then first obtained by least square fitting to the Murrell-Sorbie function (n=3) and the modified Murrell-Sorbie+c6 function, respectively. The present results show that the calculated results based on the Murrell-Sorbie function (n=3) are in better agreement with the experimental values. Calculation results in the present work may provide theoretical supports for the further study of PS molecular ion.

PS； Molecular structure； Potential energy function； Spectroscopic constants

103969/j.issn.1000-0364.2015.02.004

2013-12-10

國家自然科學基金(11304022, 11347010)；湖北省教育廳科學研究項目(Q20131208, T201204)；長江大學優秀青年教師支持計劃(cyq201321, cyq201322)；長江大學基礎學科科學研究發展基金支持計劃(2013cjp10)

蔡昌梅(1973—)，女，湖北荊州人，講師，從事大學物理的教學.E-mail: cmcai@yangtzeu.edu.cn

趙俊. E-mail: zhaojun@yangtzeu.edu.cn

O64

A

1000-0364(2015)02-0195-06