多級壓縮錐導/吻切錐乘波體設計與對比分析

呂偵軍，王江峰

(南京航空航天大學 航空宇航學院，南京 210016)

對于以吸氣式超燃沖壓發動機為動力的高超聲速飛行器而言，需要飛行器前體為發動機提供氣流壓縮、減速增壓等，以確保超燃沖壓發動機的啟動與燃燒，而乘波體可以很好地擔當這一任務.自1959 年 Nonweiler［1］首先提出“乘波”概念以來，各種乘波體設計方法相繼被提出，國內外研究者已對其開展了廣泛的研究，乘波體也被應用到高超聲速飛行器的設計中去.Rasmussen等［2-3］提出的錐導乘波體設計方法和Sobieczky等［4-5］提出的吻切錐乘波體設計方法都是較為經典的乘波體設計方法.王卓、錢翼稷［6］對比分析了錐型流理論、吻切錐理論及吻切軸對稱理論生成的不同乘波機外形.劉嘉、王發民［7-8］、姚文秀等［9］提出了用相交楔錐流場構造乘波構型飛行器前體的方法，利用該方法可以生成二級壓縮乘波體.呂浩宇等［10］研究了乘波構型飛行器前體和磁流體進氣道一體化設計，得出對進氣道引入磁流體流動控制技術不僅可以將高溫高馬赫數來流中的部分能量轉化為電能，還有利于提高燃燒室的熱效能，磁流體流動控制技術可以有效地提高進氣道的性能.賀旭照等［11-12］提出密切曲面內錐乘波前體進氣道(Osculating Inward turning Cone Waverider Inlet，OICWI)的一體化設計方法.張紅文等［13］研究了乘波外形/軌跡一體化設計，獲得了滿足全局最大航程要求的最優氣動外形.

對于已經進行過飛行演示驗證的以吸氣式超燃沖壓發動機為動力的高超聲速飛行器來說，X-43［14］前體采用的是三級壓縮(Three Stage Compression，TSC)，X-51［15］前體采用的是二級壓縮.目前，主要設計方法設計出的乘波體都只能進行一次壓縮，壓縮效率明顯不夠，需要進氣道進行進一步的壓縮，這增加了進氣道的設計難度，也使進氣道內流動變得復雜.因此，開展具有多級壓縮功能的乘波體設計技術研究可以擴大乘波體在高超聲速飛行器設計方面的工程應用前景.本文將發展的多級壓縮乘波體設計方法同時應用到錐導乘波體和吻切錐乘波體設計中去，通過該設計方法設計得到了三級壓縮錐導乘波體(Three-Stage Compression Cone-derived Waverider，TSC-ConeWR)和三級壓縮吻切錐乘波體(Three-Stage Compression Osculating Cone Waverider，TSC-OSConeWR)，數值模擬計算了其在設計無粘條件下和粘性條件下的升阻力系數、流量系數和總壓恢復系數，并對三級壓縮錐導和吻切錐乘波體的性能進行了對比分析.

1 多級壓縮乘波體設計方法

1.1 基準流場

在多級壓縮乘波體設計方法中，基準流場采用的均是Taylar-Maccoll流動，即零攻角圓錐繞流，控制方程為

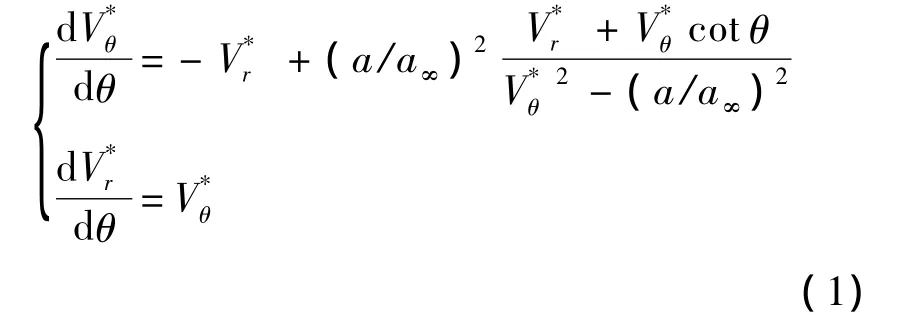
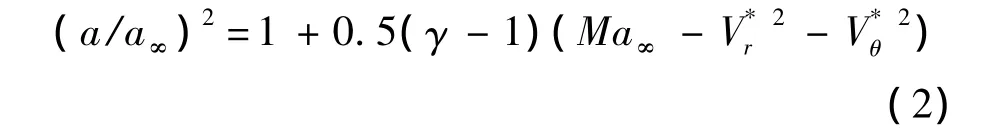
由斜激波關系式求出式(1)的初始條件為

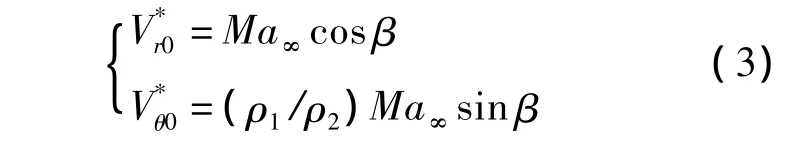
式中:β為激波角;ρ1為激波前密度;ρ2為激波后密度;Ma∞為來流馬赫數.通過式(1)和式(3)可以求得零攻角圓錐繞流的近似解.

1.2 設計方法

多級壓縮乘波體設計方法是基于吻切錐原理，吻切錐原理［4］指出一般三維超聲速流動運動方程都可以在二階精度范圍內用一個軸對稱流的運動方程來逼近.在多級壓縮乘波體設計方法中各級壓縮流場均用零攻角圓錐繞流流場來逼近.下文生成的多級壓縮錐導乘波體和多級壓縮吻切錐乘波體均是三級壓縮，因此以三級壓縮乘波體為例介紹多級壓縮乘波體的設計方法.

首先，構造如圖1所示的具有3道錐形激波的設計預期流場，3道錐形激波面相交于底部同一個圓上，3道錐形激波相對于來流的激波角分別為 β1、β2和 β3，并且需滿足:

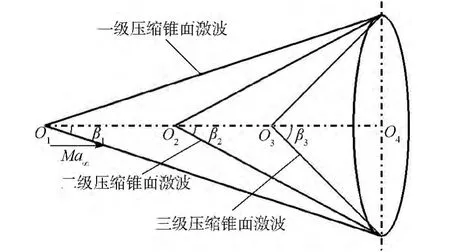
圖1 三級壓縮錐形激波的設計預期流場Fig.1 Design expected flow field of TSC conical shockwave

三級壓縮乘波體的第1級壓縮的基準流場如圖2，由于第1級壓縮基準流場是零攻角的，因此可以按照常規乘波體設計方法在零攻角圓錐繞流流場中流線追蹤獲得一級壓縮面.當流線追蹤至圖3所示的二級錐形激波面時，流線與二級錐形激波面有一個交點A，可以在一級壓縮基準流場中求出A點的流動參數，將其作為二級壓縮基準流場的來流條件，并將A點作為二級壓縮面流線追蹤的起始點.但A點流動方向與軸線O2O4之間存在攻角α1，在這種情況下不可以用零攻角圓錐繞流來構造二級壓縮基準流場.

多級壓縮乘波體設計方法主要解決的是二級及后面級壓縮基準流場的構造問題.應用吻切錐原理在圖3中將中軸線O2O4繞O2沿圖示方向旋轉α1度，使新得到的軸線O2O5與A點的流動方向平行.經過這樣處理后，A點流動方向相對于圖3中新的二級壓縮基準流場是零攻角的，因此新的二級壓縮基準流場可以用零攻角圓錐繞流(Taylar-Maccoll流動)來構造，其二級壓縮的實際激波角為β2－α1.三級壓縮的基準流場采用同樣的方法進行處理，如圖4，B點的流動相對于軸線O2O5存在攻角α2，經過上述處理后，新的三級壓縮實際激波角為 β3－α1－α2.

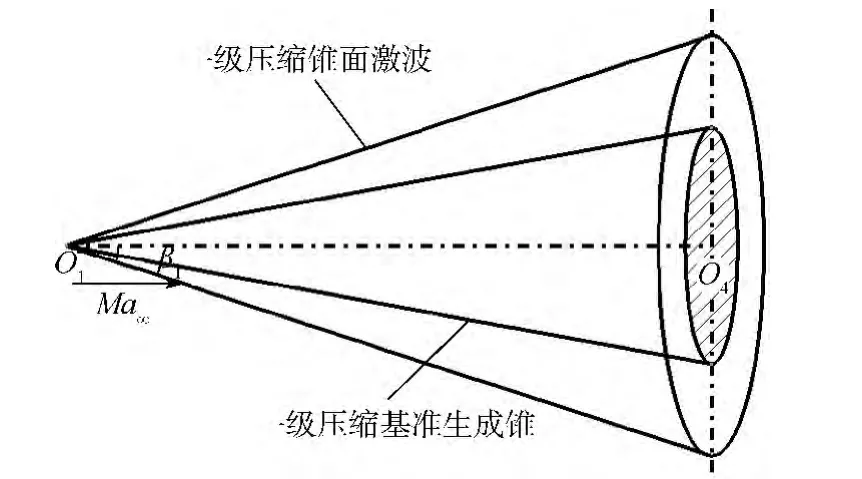
圖2 第1級壓縮基準流場Fig.2 Reference flow field for first-stage compression

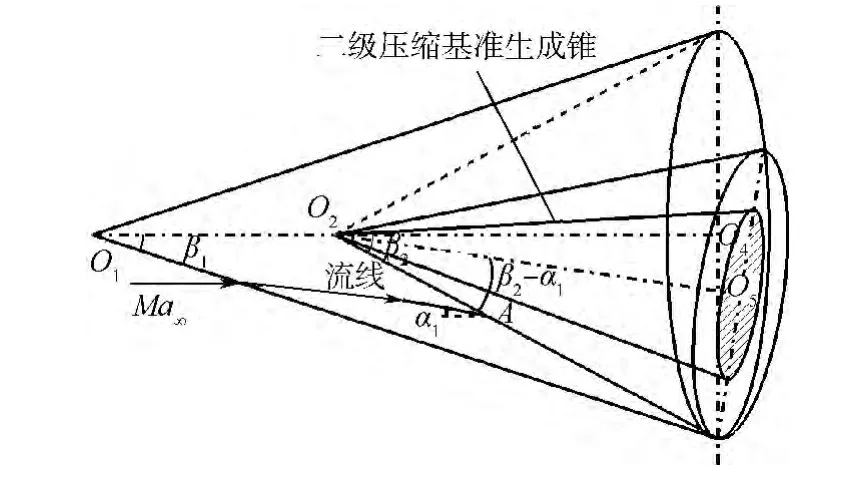
圖3 第2級壓縮基準流場Fig.3 Reference flow field for second-stage compression

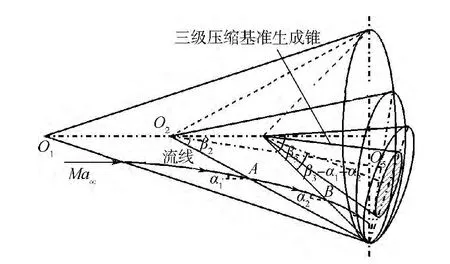
圖4 第3級壓縮基準流場Fig.4 Reference flow field for third-stage compression

2 多級壓縮錐導/吻切錐乘波體設計

吻切錐乘波體外形的生成是由流動捕獲曲線(Flow Capture Curve，FCC)和進氣道捕獲曲線(Inlet Capture Curve，ICC)決定的，構造如圖5所示的FCC曲線和ICC曲線，這兩條曲線的表達式為

FCC曲線:

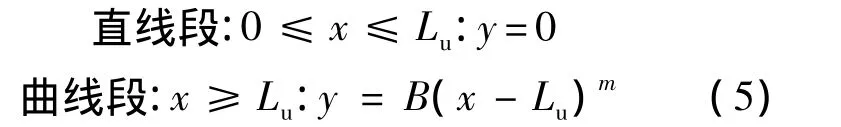
ICC曲線:

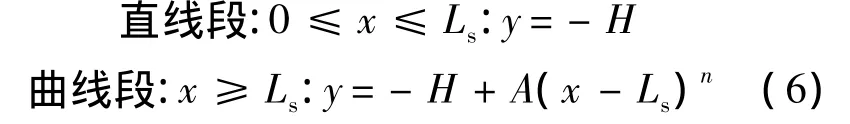
式中:Lu為FCC曲線直線段的長度;Ls為ICC曲線直線段的長度;H=L tanβ1，L為乘波體的長度，β1為一級壓縮激波角.給定Lu、Ls、指數m和n、系數k，A和B可以通過幾何關系求得;圖5中ycoj=－kH表示FCC曲線和ICC曲線交點的位置.

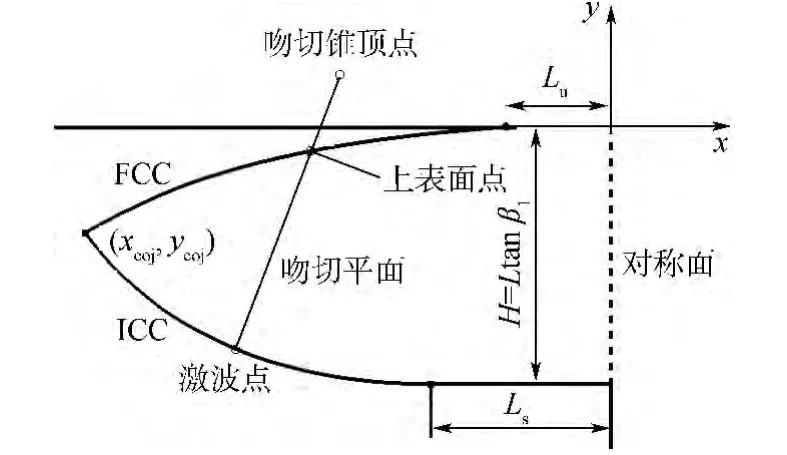
圖5 吻切錐乘波體ICC和FCC曲線定義Fig.5 Curve definition of ICC and FCC for osculating cone waverider

在過ICC曲線段的任意一點的吻切平面(Osculating Plane，OP)內，通過上述多級壓縮乘波體設計方法獲得該平面內的流線.ICC直線段的流線通過斜激波關系式求得.而錐導乘波體設計是吻切錐乘波體設計方法的一個特例，即相當于錐導乘波體的ICC曲線為一段圓弧，各點的曲率半徑為恒定值［16］.

選取吻切錐乘波體的幾何參數:乘波體長度L=5.0m;FCC直線段長度 Lu=0.2m;ICC直線段長度 Ls=0.35m;xcoj= －2.0m;指數 m=4、n=2.5;系數 k=0.45;β1=12°，將這些參數代入式(5)和式(6)并根據幾何關系即可得到FCC和ICC曲線.為了對比三級壓縮錐導和吻切錐乘波體的性能，使三級壓縮錐導乘波體的前緣在XY平面的投影與吻切錐乘波體的FCC曲線相同，即這兩種乘波體具有在XY平面的投影形狀相同的前緣.

根據多級壓縮乘波體設計方法，編寫設計程序設計得到了來流馬赫數6.0;壓強1 197 Pa;密度0.01841 kg/m3;溫度226.5K;三級激波角分別為 β1=12°、β2=18°、β3=25°設計條件下的 3 級壓縮錐導和吻切錐乘波體，如圖6、圖7所示.圖中綠色部分為一級壓縮面，淺藍部分為二級壓縮面，深藍部分為三級壓縮面.

圖6 三級壓縮錐導乘波體和吻切錐乘波體Fig.6 TSC cone-derived waverider and osculating cone waverider

圖7 三級壓縮錐導乘波體和吻切錐乘波體下表面Fig.7 Lower surface of TSC cone-derived waverider and osculating cone waverider

3 數值模擬分析

3.1 無粘條件

由于多級壓縮乘波體設計都是基于無粘條件的，為了驗證多級壓縮乘波體設計方法的正確性，采用Euler求解器對三級壓縮錐導和吻切錐乘波體進行了數值模擬驗證.圖8給出了三級壓縮錐導和吻切錐乘波體在設計條件下的下表面密度云圖，圖9為該條件下的激波結構圖.

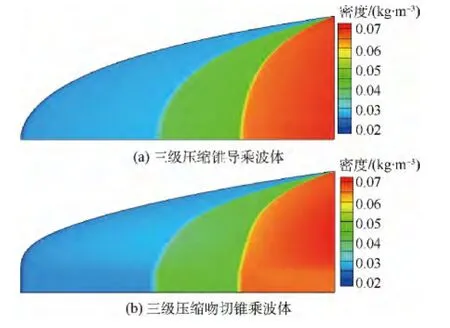
圖8 三級壓縮乘波體下表面密度云圖Fig.8 Density contours of TSC waverider’s lower surface

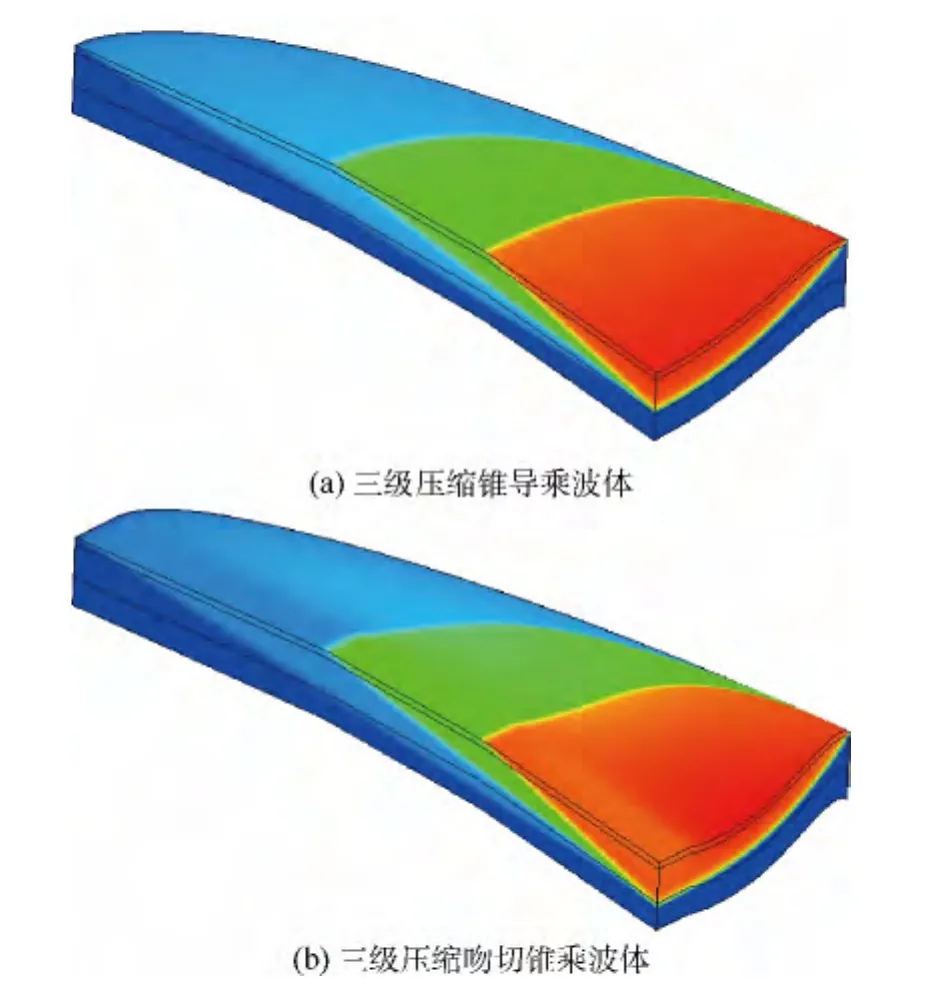
圖9 三級壓縮乘波體激波結構圖Fig.9 Shockwave structural diagram of TSC waverider

由數值模擬結果圖可以得出，三級壓縮錐導和吻切錐乘波體下表面產生激波的位置與圖7相吻合，并且3道激波按照設計預期相交于乘波體底部平面內.圖10給出了三級壓縮吻切錐乘波體底部截面的密度云圖，3道激波在圖中相交的位置與ICC曲線吻合較好.

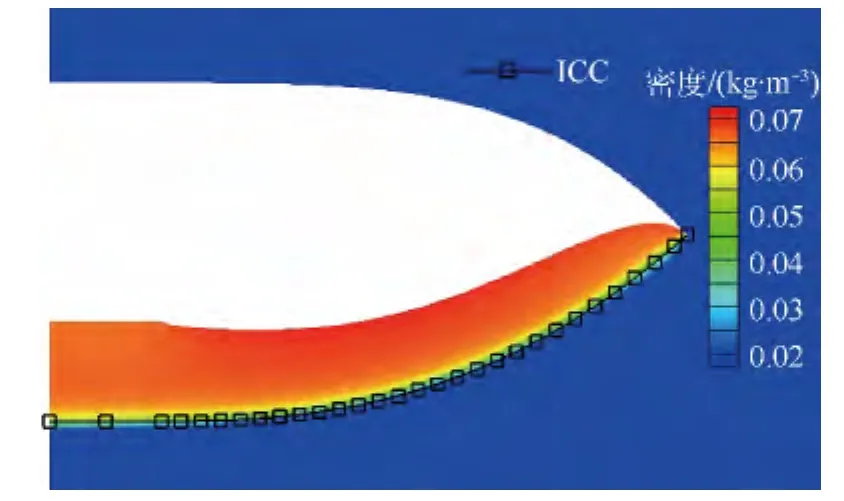
圖10 三級壓縮吻切錐乘波體底部截面密度云圖Fig.10 Density contours of TSC osculating cone waverider’s bottom section

預壓縮性能、總壓恢復系數、升阻比等性能是評價乘波體的重要性能指標.流量系數σ為前體預壓縮性能的評價參數，代表了氣流到達進氣道進口處的質量通量的相對變化率，表達式為σ=ρu/(ρu)∞.總壓恢復系數 η =P02/P01為底部切面內激波與乘波體間的面積平均總壓與來流總壓的比值，它反映了氣流經過前體后的能量損失.

通過數值模擬對三級壓縮錐導乘波體以及三級壓縮吻切錐乘波體的升阻力性能、流量系數和總壓恢復系數進行了計算，計算結果見表1和表2.參考面積取乘波體下表面的面積.

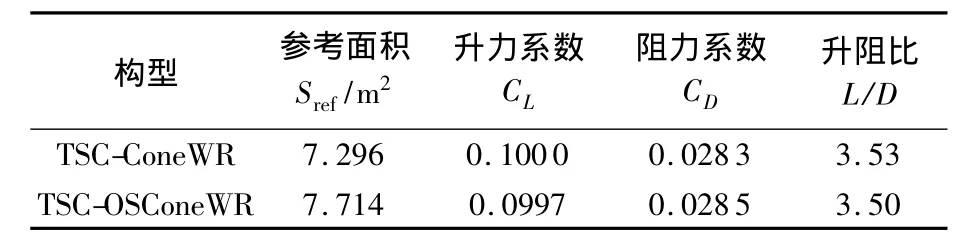
表1 三級壓縮乘波體無粘氣動性能參數Table 1 Inviscid aerodynamic performance parameters of TSC waverider

表 2三級壓縮乘波體無粘壓縮性能參數Table 2 Inviscid compression performance parameters of TSC waverider

在設計條件下，三級壓縮錐導與吻切錐乘波體的無粘性能參數基本一致，這是由于三級壓縮錐導乘波體3個壓縮面的面積分別為3.066、1.868和2.362m2，面積比為1∶0.609∶0.770;三級壓縮吻切錐乘波體3個壓縮面的面積分別為3.226、1.961 和 2.527 m2，面 積 比 為1∶0.608∶0.783，兩者 3 個壓縮面的面積比基本相同，并且其三級壓縮激波角相同，從圖8中看出密度云圖分布也一致，因此其性能參數基本相同.

3.2 粘性條件

以上三級壓縮錐導和吻切錐乘波體的設計與分析都是在無粘條件下的，但在實際應用時，粘性問題不可避免，因此需要研究多級壓縮乘波體在粘性條件下的性能，在研究多級壓縮乘波體粘性問題時，湍流模型選取S-A模型.

表3與表4分別為三級壓縮錐導和吻切錐乘波體在粘性條件下的升阻力與壓縮性能數據，與無粘條件下一樣，各項性能參數也基本相同.圖11為三級壓縮錐導和吻切錐乘波體在粘性條件下的等壓線圖.

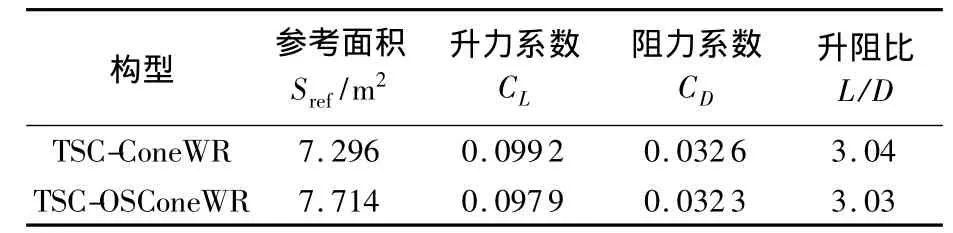
表3 三級壓縮乘波體粘性氣動性能參數Table 3 Viscous aerodynamic performance parameters of TSC waverider

表4 三級壓縮乘波體粘性壓縮性能參數Table 4 Viscous compression performance parameters of TSC waverider

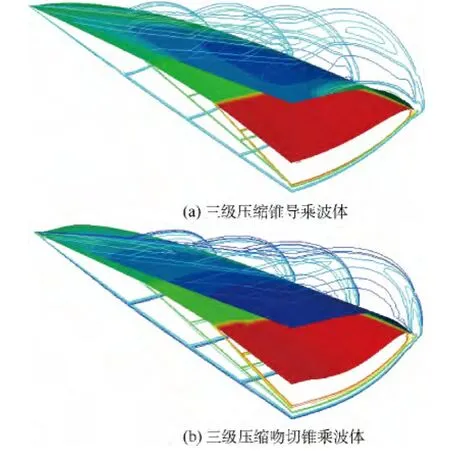
圖11 三級壓縮乘波體等壓線圖Fig.11 Pressure contours of TSC waverider

由表2和表4可以得出，三級壓縮錐導乘波體在無粘與粘性條件下的壓縮性能都要略優于三級壓縮吻切錐乘波體.相比于無粘條件，三級壓縮錐導和吻切錐乘波體的升阻比分別下降了13.88%和13.43%.在乘波體的前緣處出現了一些溢流，但對升力的影響較小，依然具有良好的乘波性能，升阻比的降低主要是由考慮粘性后阻力的增加導致的.由粘性產生的邊界層相當于增加了乘波體下表面的厚度，使各級激波角有所增大，如圖11所示3道激波在底部分別相距一段很小的距離，這個問題可以根據三級壓縮乘波體在實際應用時給定一定的攻角來克服.

為了研究多級壓縮乘波體在非設計狀態下的性能，對三級壓縮錐導乘波體(TSC-ConeWR)在馬赫數 6.0、攻角 4°和馬赫數 5.0、攻角 4°條件下的流場進行了計算.表5匯總對比了三級壓縮錐導乘波體在無粘和粘性設計條件下以及粘性非設計條件下的性能.

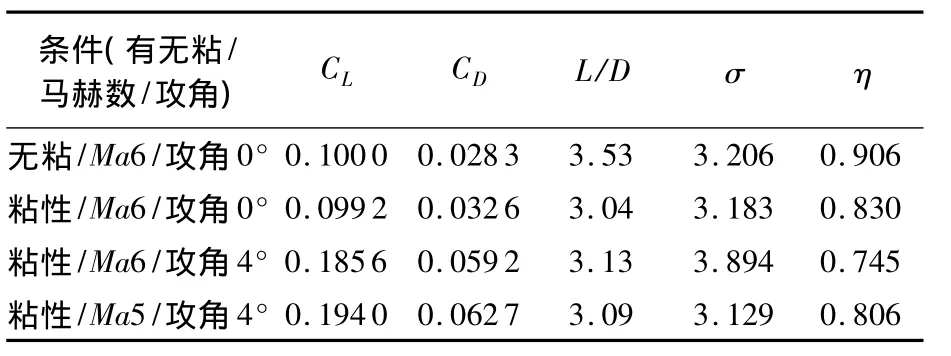
表5 三級壓縮錐導乘波體不同條件下氣動性能對比Table 5 Aerodynamic performance comparison of TSC cone-derived waverider in different conditions

計算結果表明，給定4°的攻角的情況下，攻角的增加相當于增大了激波角，使壓縮加劇，總壓損失變大.由于激波角增大，激波后壁面的壓力也增大，使升力和阻力同時增大，并且在馬赫數5.0和6.0的條件下，升阻比都有所增大.

圖12為三級壓縮錐導乘波體在來流馬赫數6.0、攻角 4°和來流馬赫數 5.0、攻角 4°條件下的等壓線圖.馬赫數6.0、攻角4°的等壓線圖中3道激波交匯在底部截面上，驗證了上文提到的通過給定一定的攻角可以克服在設計條件下考慮粘性后3道激波在底部截面上相距一小段距離的問題.馬赫數5.0、攻角4°的圖中，3道激波還相距很小的距離，可以繼續增大攻角來解決.從流場圖中看，相較于設計條件，前緣的溢流程度有所增大，但依然保持了良好的乘波性能.

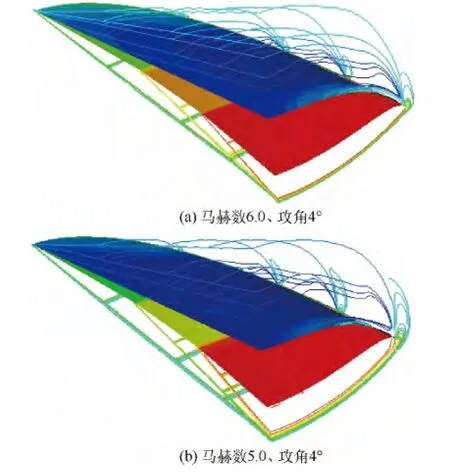
圖12 三級壓縮錐導乘波體非設計狀態等壓線圖Fig.12 Pressure contours of TSC waverider off design condition

4 結論

本文在吻切錐理論的基礎上發展了一種多級壓縮乘波體設計方法，對由該設計方法設計得到的多級壓縮乘波體進行了研究，研究結果表明:

1)將多級壓縮乘波體設計方法同時應用于錐導和吻切錐乘波體，獲得的三級壓縮錐導和吻切錐乘波體通過數值模擬結果驗證了設計方法的正確性.

2)在粘性條件下，三級壓縮錐導和吻切錐乘波體的流量系數分別為3.183和3.084，多級壓縮乘波體充分發揮了前體的預壓縮性能.

3)對于相同設計條件和具有相同前緣投影的三級壓縮錐導乘波體和吻切錐乘波體，其升阻力性能基本相同，壓縮性能三級壓縮錐導乘波體要略優于三級壓縮吻切錐乘波體，但錐導乘波體的進氣道入口曲線必須是圓弧形的，而吻切錐乘波體更能適應一般形狀的進氣道.在實際應用時，應按照具體要求選擇應用何種乘波體.

4)三級壓縮錐導乘波體在非設計狀態依然表現出良好的乘波性能和壓縮性能.

為使獲得的多級壓縮乘波體更接近工程應用條件，仍需要對乘波體普遍存在的尖銳前緣處氣動加熱問題開展研究，找到合適的前緣鈍化方法，既保證乘波體的性能，又能有效地降低前緣的氣動加熱.

References)

［1］ Nonweiler TR F.Aerodynamic problems of manned space vehicles［J］.Journal of Royal Aeronautical Society，1959，63(9):512-528.

［2］ Rasmussen M L，Jischke M C，Daniel D C.Experimental forces and moments on cone-derived waveriders for M∞=3 to 5［J］.Journal of Spacecraft and Rockets，1982，19(6):592-598.

［3］ Rasmussen M L，Jischke M C，Daniel D C.Waverider configurations derived from inclined circular and elliptic cones［J］.Journal of Spacecraft and Rockets，1980，17(6):537-545.

［4］ Sobieczky H，Dougherty F C，Jones K D.Hypersonic waverider design from given shock waves［C］∥First International Waverider Symposium.Maryland:University of Maryland，1990.

［5］ Jones K D，Sobieczky H，Seebass A R，et al，Waverider design for generalized shock geometries［J］.Journal of Spacecraft and Rockets，1995，32(6):957-963.

［6］王卓，錢翼稷.乘波機外形設計［J］.北京航空航天大學學報，1999，25(2):180-183.Wang Z，Qian Y J.Waverider configuration design［J］.Journal of Beijing University of Aeronautics and Astronautics，1999，25(2):180-183(in Chinese).

［7］劉嘉，王發民.乘波前體構型設計與壓縮性能分析［J］.工程力學，2003，20(6):130-134.Liu J，Wang F M.Waverider configuration design and forebody compressibility analysis［J］.Engineering Mechanics，2003，20(6):130-134(in Chinese).

［8］王發民，李立偉，姚文秀，等.乘波飛行器構型方法研究［J］.力學學報，2004，36(5):513-519.Wang FM，Li LW，Yao W X，et al.Research on waverider configuration method［J］.Acta Mechanica Sinica，2004，36(5):513-519(in Chinese).

［9］姚文秀，雷麥芳，楊耀棟，等.高超聲速乘波飛行器氣動實驗研究［J］.宇航學報，2002，23(6):82-85.Yao W X，Lei M F，Yang Y D，et al.An aerodynamic experiment research of the hypersonic waverider vehicle［J］.Journal of Astronautics，2002，23(6):82-85(in Chinese).

［10］呂浩宇，李椿萱，曹德一.乘波構型飛行器磁流體進氣道一體化概念設計［J］.北京航空航天大學學報，2008，34(10):1130-1134.Lü H Y，Lee C X，Cao D Y.Conceptual study on integrated design of magneto hydrodynamic by pass scramjet for a waverider based hypersonic vehicle［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(10):1130-1134(in Chinese).

［11］賀旭照，倪鴻禮.密切內錐乘波體設計方法和性能分析［J］.力學學報，2011，43(5):803-808.He X Z，Ni H L.Osculating inward turning cone(OIC)waverider design methods and performance analysis［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43(5):803-808(in Chinese).

［12］賀旭照，周正，毛鵬飛，等.密切曲面內錐乘波前體進氣道設計和試驗研究［J］.實驗流體力學，2014，28(3):39-44.He X Z，Zhou Z，Mao P F，etal.Design and experimental study of osculating inward turning cone waverider/inlet(OICWI)［J］.Journal of Experiments in Fluid Mechanics，2014，28(3):39-44(in Chinese).

［13］張紅文，張科南，陳萬春.帶靜態參數的高超聲速飛行器軌跡優化算法［J］.北京航空航天大學學報，2014，40(2):141-147.Zhang HW，Zhang K N，Chen W C.Indirect method for trajectory optimization of hypersonic vehicle with static parameters［J］.Journal of Beijing University of Aeronautics and Astronautics，2014，40(2):141-147(in Chinese).

［14］ Harsha P T，Keel L C，Castrogiovanni A，et al.X-43A vehicle design and manufacture，AIAA-2005-3334［R］.Reston:AIAA，2005.

［15］ Matthew P B，Steven P S.Effect of free stream noise on roughness-induced transition for the X-51A forebody［J］.Journal of Spacecraft and Rockets，2008，45(6):1106-1116.

［16］陳小慶，侯中喜，何烈堂，等.吻切錐乘波構型參數化設計與正交試驗分析［J］.推進技術，2010，31(4):385-389.Chen X Q，Hou Z X，He L T，et al.Parameterized design and orthogonal experiment analysis of osculating-cone waverider［J］.Journal of Propulsion Technology，2010，31(4):385-389(in Chinese).