含非對(duì)稱摩擦平面運(yùn)動(dòng)剛體動(dòng)力學(xué)LCP方法

王曉軍，王琪

(1.常州工學(xué)院 機(jī)電學(xué)院，常州 213002;2.北京航空航天大學(xué) 航空科學(xué)與工程學(xué)院，北京 100191)

物體間的接觸、碰撞和摩擦現(xiàn)象是普遍存在的.如航天器的空中對(duì)接、飛機(jī)的著陸、步行機(jī)器人在地面上行走、機(jī)械手抓取工件以及具有非理想約束鉸鏈(含間隙與摩擦)的機(jī)械系統(tǒng)運(yùn)轉(zhuǎn)等，都存在物體間的接觸與分離、接觸點(diǎn)的粘滯與滑移(stick-slip)等現(xiàn)象.如何描述物體間接觸或碰撞時(shí)的相互作用力，如何給出粘滯(stick)與滑移判別的計(jì)算方法，是建立系統(tǒng)動(dòng)力學(xué)方程并通過(guò)數(shù)值仿真分析其動(dòng)力學(xué)行為的重要問(wèn)題之一.

20世紀(jì)末和21世紀(jì)初，人們利用多種接觸力模型研究物體的接觸與碰撞問(wèn)題，如Kelvin-Voigt接觸力模型、Hertz接觸力模型、Hunt-Crossley接觸力模型和Lankarani-Nikravesh(L-N)接觸力模型等［1］.目前被廣泛使用的摩擦模型有Coulomb干摩擦模型、修正的Coulomb摩擦模型、粘性摩擦模型、Stribeck摩擦模型［2］和 Dahl摩擦模型［3］等，Coulomb摩擦模型被認(rèn)為是較簡(jiǎn)單的摩擦模型［1，4］.

文獻(xiàn)［5］利用修正的Kelvin模型研究了鄰近的兩個(gè)建筑物的碰撞問(wèn)題.文獻(xiàn)［6］利用L-N接觸力模型研究了含間隙轉(zhuǎn)動(dòng)鉸的速回機(jī)構(gòu)的動(dòng)力學(xué)建模與數(shù)值算法問(wèn)題，并給出了接觸點(diǎn)檢測(cè)的數(shù)值方法，該文獻(xiàn)未涉及摩擦問(wèn)題.文獻(xiàn)［7］利用L-N接觸力模型、線彈性接觸力模型和修正的Coulomb摩擦模型研究了含間隙滑移鉸機(jī)械系統(tǒng)的動(dòng)力學(xué)建模與數(shù)值算法問(wèn)題，當(dāng)滑移鉸中的物塊頂角與滑道碰撞時(shí)用L-N接觸力模型，當(dāng)物塊的一個(gè)邊(面)與滑道接觸時(shí)用線彈性接觸力模型.該文獻(xiàn)采用修正的Coulomb摩擦模型無(wú)法反映物塊與滑道間的stick-slip現(xiàn)象.文獻(xiàn)［8-10］分別研究了具有含摩擦轉(zhuǎn)動(dòng)鉸和滑移鉸平面多剛體系統(tǒng)動(dòng)力學(xué)的建模與數(shù)值算法問(wèn)題，文獻(xiàn)中均采用Coulomb干摩擦模型，應(yīng)用試算法或線性互補(bǔ)方法有效地解決了stick-slip運(yùn)動(dòng)狀態(tài)的切換問(wèn)題，但無(wú)法反映鉸鏈處的碰撞問(wèn)題，當(dāng)鉸鏈的間隙不能忽略時(shí)，該方法則不適用.文獻(xiàn)［11］研究了非對(duì)稱庫(kù)侖干摩擦模型對(duì)振動(dòng)驅(qū)動(dòng)機(jī)械系統(tǒng)動(dòng)力學(xué)行為的影響，豐富了非光滑系統(tǒng)動(dòng)力學(xué).

本文基于非光滑動(dòng)力學(xué)理論，給出了一種物體接觸點(diǎn)含對(duì)稱或非對(duì)稱Coulomb干摩擦的平面運(yùn)動(dòng)剛體動(dòng)力學(xué)的建模與數(shù)值計(jì)算方法.該方法是將研究對(duì)象視為剛體，考慮接觸點(diǎn)的局部變形，將物體間的法向接觸力表示成嵌入量與嵌入速度的函數(shù);摩擦模型采用對(duì)稱或非對(duì)稱的Coulomb干摩擦模型;利用事件驅(qū)動(dòng)法，將由于摩擦引起的stick-slip運(yùn)動(dòng)狀態(tài)切換的判斷問(wèn)題以及處于粘滯(stick)狀態(tài)時(shí)靜摩擦力的計(jì)算問(wèn)題轉(zhuǎn)化成線性互補(bǔ)問(wèn)題的求解.該方法與傳統(tǒng)方法相比，不包含與接觸-分離相關(guān)的互補(bǔ)量，因此線性互補(bǔ)方程的維數(shù)低，計(jì)算效率高，將適用于對(duì)稱Coulomb干摩擦的互補(bǔ)算法推廣到非對(duì)稱Coulomb干摩擦模型.最后通過(guò)數(shù)值算例分析了非光滑平面運(yùn)動(dòng)剛體的動(dòng)力學(xué)特性，并驗(yàn)證了該方法的有效性.

1 接觸力學(xué)模型

1.1 法向接觸力模型

當(dāng)物體間接觸或碰撞時(shí)，若考慮物體的局部變形，則一個(gè)物體會(huì)局部嵌入到另一個(gè)物體中，其法向嵌入量用δ表示，如圖1所示.用Hertz接觸模型，法向接觸力FN可表示［7］為

式中:K為廣義剛度系數(shù);n為指數(shù)，其通常的取值范圍為［1，1.5］.當(dāng)物體是點(diǎn)(局部)接觸時(shí)，該指數(shù)n=1.5，將接觸部位近似為半徑為R的圓弧，其廣義剛度系數(shù)可表示［7］為

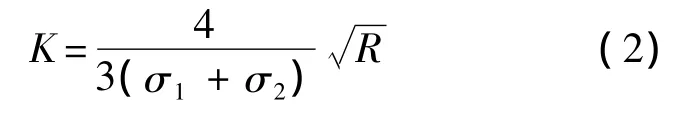
式中:

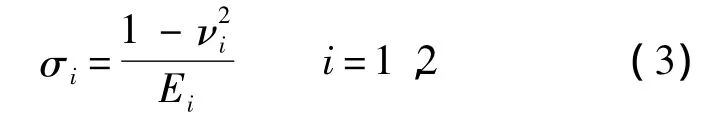
其中:Ei和νi分別為兩接觸物體的彈性模量和泊松比.

圖1 兩物體間的接觸模型Fig.1 Contact model between two bodies

由于Hertz接觸力模型中不含阻尼項(xiàng)，這與實(shí)際情況有一定的差距.文獻(xiàn)［12］給出了一種非線性粘彈性接觸力模型，其表達(dá)式為

式中:c為廣義阻尼系數(shù)，該接觸力模型中的彈性項(xiàng)δK為δ的線性函數(shù).文獻(xiàn)［13］使用另一種非線性粘彈性接觸力模型，其表達(dá)式為

該接觸力的彈性項(xiàng)和阻尼項(xiàng)均為非線性的，能較好地刻畫(huà)接觸力的特性.文獻(xiàn)［1］還給出了一種隱式的法向接觸力模型:

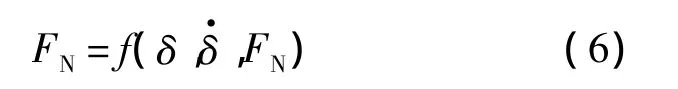
接觸力模型的研究還在不斷的深入和完善.

1.2 切向接觸力模型

機(jī)械系統(tǒng)中常用的摩擦模型有多種［2-3］，其中Coulomb摩擦模型又可分為Coulomb干摩擦模型和修正的Coulomb摩擦模型，前者是相對(duì)速度的非連續(xù)函數(shù)(數(shù)值計(jì)算存在困難)，后者是相對(duì)速度的連續(xù)函數(shù)(不易反映摩擦的靜動(dòng)態(tài)特性)［14］.本文將采用非對(duì)稱Coulomb干摩擦模型，該模型的數(shù)學(xué)表達(dá)式［11］為

式中:

其中:Fτ為作用在物體上的摩擦力在接觸面切向上的投影;μ+、μ－和 μ0+、μ0－分別為物體間的正、負(fù)向動(dòng)摩擦因數(shù)以及正、負(fù)向靜摩擦因數(shù)(當(dāng)μ+=μ－，μ0+=μ0－時(shí)，即為對(duì)稱的 Coulomb 干摩擦模型分別為接觸點(diǎn)的相對(duì)速度和相對(duì)切向加速度.由式(7)～式(9)可知，當(dāng)時(shí)，接觸點(diǎn)處于stick狀態(tài)，摩擦力的取值是一個(gè)范圍.

2 非光滑動(dòng)力學(xué)方程及其數(shù)值求解算法

2.1 非光滑動(dòng)力學(xué)方程

若設(shè)物體與固定面接觸時(shí)，其接觸面的法向量平行于y軸，用Newton-Euler方法可得平面運(yùn)動(dòng)剛體的動(dòng)力學(xué)方程:

因?yàn)榍度肓亢颓度胨俣瓤梢员硎緺顟B(tài)變量的函數(shù)，因此，從式(5)不難看出，法向接觸力FNi是狀態(tài)變量)的函數(shù);由式(7)和式(8)可知，當(dāng)時(shí)，摩擦力Fτi也是狀態(tài)變量的函數(shù).根據(jù)狀態(tài)變量可計(jì)算出FNi和Fτi.

2.2 Coulomb摩擦定律的互補(bǔ)關(guān)系

非光滑動(dòng)力學(xué)方程數(shù)值計(jì)算的難點(diǎn)在于物體間接觸點(diǎn)stick-slip狀態(tài)切換的判斷以及處于stick狀態(tài)時(shí)摩擦力的計(jì)算.本文通過(guò)建立非對(duì)稱Coulomb摩擦定律的互補(bǔ)關(guān)系，將上述計(jì)算問(wèn)題轉(zhuǎn)化為線性互補(bǔ)問(wèn)題的求解.

可將該摩擦余量的概念推廣到非對(duì)稱Coulomb干摩擦模型，對(duì)應(yīng)的正向摩擦余量和負(fù)向摩擦余量可分別定義為

由式(12)可得

由式(14)可得

2.3 動(dòng)力學(xué)方程的求解算法

由式(13)、式(15)、式(17)和方程式(10)聯(lián)立，可以得到線性互補(bǔ)方程:

式中:wi1、wi2、Hxi和 Hθi均為狀態(tài)變量的函數(shù).應(yīng)用線性互補(bǔ)問(wèn)題(LCP)的數(shù)值算法求解式(18)，可得，再由式(13)，可求出摩擦力 Fτi，將其代入動(dòng)力學(xué)方程式(10)中，然后用常微分方程的數(shù)值方法求解該方程.

3 算例

3.1 算例模型

設(shè)圖2所示箱體為均質(zhì)體，其質(zhì)量為m，邊長(zhǎng)分別是2a和2b，可與水平固定面發(fā)生接觸和摩擦，圖中C為箱體的質(zhì)心，其坐標(biāo)為(x，y)，用本文給出的方法對(duì)其進(jìn)行動(dòng)力學(xué)仿真.

圖2 算例中的箱體Fig.2 Slider in this example

該箱體頂角1和頂角2的嵌入量可分別表示為

箱體頂角1和頂角2與固定面接觸時(shí)的切向(沿x軸方向)速度可分別表示為

設(shè)系統(tǒng)參數(shù)為:m=2.0 kg，a=0.4m，b=0.3m;接觸力模型由式(5)給出，其中 n=1.5，K=2.96 ×107N/m1.5，c=1.89 ×106N·s/m2.

3.2 數(shù)值仿真分析

算例1 箱體在重力作用下自由下落并與地面發(fā)生接觸.設(shè)摩擦模型為對(duì)稱的Coulomb干摩擦模型，其摩擦因數(shù)為 μ+=μ－=0.3，μ0+=μ0－=0.4;初始條件為 x0=0，y0=0.8m，θ0=

圖3給出了箱體頂角1和頂角2的法向接觸力FN1和FN2的時(shí)間歷程圖;圖4給出了δ1和δ2的時(shí)間歷程圖.由此可以看出，箱體的頂角2先與地面發(fā)生碰撞，其碰撞速度為4.96m/s，然后該點(diǎn)發(fā)生第二次碰撞，其碰撞速度為0.65m/s;隨后頂角1與地面碰撞，其碰撞速度為3.16m/s;兩個(gè)頂角經(jīng)過(guò)幾次碰撞后，箱體最終靜止在地面上.由于碰撞速度不同，對(duì)應(yīng)的碰撞沖擊力的峰值也就不同.

圖5給出了x、y和θ的時(shí)間歷程圖，其運(yùn)動(dòng)狀態(tài)與箱體受力狀態(tài)吻合.圖6給出了箱體質(zhì)心速度以及箱體所受摩擦力的時(shí)間歷程圖.由于箱體頂角2前兩次與地面發(fā)生碰撞時(shí)，有向左的相對(duì)運(yùn)動(dòng)，因此摩擦力的方向向右，在其作用下，物體的質(zhì)心有向右的速度.當(dāng)箱體與地面再次發(fā)生碰撞時(shí)，由于運(yùn)動(dòng)速度向右，因此摩擦力向左.經(jīng)過(guò)幾次碰撞后，最終物體相對(duì)地面靜止.

圖3 F N1和F N2的時(shí)間歷程圖Fig.3 Time history diagram of F N1 and F N2

圖4 δ1和δ2的時(shí)間歷程圖Fig.4 Time history diagram ofδ1 and δ2

圖5 x、y和θ的時(shí)間歷程圖Fig.5 Time history diagram of x、y and θ

圖6 和Fτ的時(shí)間歷程圖Fig.6 Time history diagram ofand Fτ

算例2 箱體放在水平地面上，其上作用一個(gè)水平力 Fx=A sin t.設(shè)摩擦因數(shù)為 μ+=0.3，μ－=0.4，μ0+=0.5，μ0－=0.6，初始條件為

算例1和算例2均用試算法進(jìn)行了驗(yàn)證，試算法與本文給出的算法所得數(shù)值結(jié)果完全吻合.

圖7 當(dāng)A=11，12，18N時(shí)x和的時(shí)間歷程圖Fig.7 Time history diagram of x andwith A=11，12，18N

4 結(jié)論

基于非光滑動(dòng)力學(xué)方法，利用線性互補(bǔ)理論，給出了一種含非對(duì)稱Coulomb干摩擦的平面運(yùn)動(dòng)剛體動(dòng)力學(xué)的數(shù)值算法.

1)將物體間的法向接觸力表示成物體間嵌入量和嵌入速度的函數(shù)，無(wú)需引入互補(bǔ)量，更易于分析物體間的接觸與分離.

2)建立了非對(duì)稱摩擦余量互補(bǔ)關(guān)系，將原適用于含對(duì)稱Coulomb干摩擦的LCP算法推廣到非對(duì)稱Coulomb干摩擦系統(tǒng)，使其具有更廣泛的適用性.

3)數(shù)值仿真算例表明，該算法易于分析非光滑系統(tǒng)中物體間的接觸與分離和stick-slip現(xiàn)象.

References)

［1］ Flores P，Ambrósio J.Kinematics and dynamics of multibody systems with imperfect joints［M］.Berlin:Springer，2008:47-66.

［2］劉麗蘭，劉宏昭，吳子英，等.機(jī)械系統(tǒng)中摩擦模型的研究進(jìn)展［J］.力學(xué)進(jìn)展，2008，38(2):200-213.Liu L L，Liu H Z，Wu Z Y，et al.An overview of friction models in mechanical systems［J］.Advances in Mechanics，2008，38(2):200-213(in Chinese).

［3］ Pennestri E，Valentini P P，Vita L.Multibody dynamics simulation of planar linkages with Dahl friction［J］.Multibody System Dynamics，2007，17(4):321-347.

［4］ Pfeiffer F，Glocker C.Multibody dynamics with unilateral contacts［M］.New York:John Wiley ＆ Sons，Inc，1996:70-91.

［5］ Ye K，Li L，Zhu H P.A modified Kelvin impact model for pounding simulation of base-isolated building with adjacent structures［J］.Earthquake Engineering and Engineering Vibration，2009，8(3):433-446.

［6］ Flores P，Ambrósio J.On the contact detection for contact-impact analysis in multibody systems［J］.Multibody System Dynamics，2010，24(1):103-122.

［7］ Flores P，Ambrosio J.Translational joints with clearance in rigid multibody systems［J］.ASME Journal of Computational and Nonlinear Dynamics，2008，3(1):011007.

［8］莊方方，王琪.含摩擦柱鉸鏈平面多體系統(tǒng)動(dòng)力學(xué)的建模和數(shù)值方法［J］.工程力學(xué)，2012，29(5):193-199.Zhuang FF，Wang Q.Modeling and numerical algorithm for planar multibody system with friction on revolute joints［J］.Engineering Mechanics，2012，29(5):193-199(in Chinses).

［9］ Wang Q，Peng H L，Zhuang F F.A constraint-stabilized method for multibody dynamics with friction-affected translational joints based on HLCP［J］.Discrete and Continuous Dynamical Systems Series B，2011，16(2):589-605.

［10］ Zhuang F F，Wang Q.Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints［J］.Multibody System Dynamics，2013，29(4):403-423.

［11］ Fang H B，Xu J.Dynamics of a three-module vibration-driven system with non-symmetric Coulomb’s dry friction［J］.Multibody System Dynamics，2012，27(4):455-485.

［12］ Kisu L.A short note for numerical analysis of dynamic contact considering impact and a very stiff spring-damper constraint on the contact point［J］.Multibody System Dynamics，2011，26(4):425-439.

［13］劉才山，陳濱，王玉玲.考慮摩擦作用的多柔體系統(tǒng)點(diǎn)-面碰撞模型［J］.中國(guó)機(jī)械工程，2000，11(6):616-619.Liu C S，Chen B，Wang Y L.The point-surface impact model considering the friction effect in flexible multi-body system［J］.China Mechanical Engineering，2000，11(6):616-619(in Chinses).

［14］王琪，莊方方，郭易圓.非光滑多體系統(tǒng)動(dòng)力學(xué)數(shù)值算法的研究進(jìn)展［J］.力學(xué)進(jìn)展，2013，43(1):101-111.Wang Q，Zhuang F F，Guo Y Y.Advances in the research on the numerical method fir non-smooth dynamics of multibody systems［J］.Advances in Mechanics，2013，43(1):101-111(in Chinese).

［15］ Pfeiffer F，F(xiàn)oerg M，Uibrich H.Numerical aspects of nonsmooth multibody dynamics［J］.Computer Methods in Applied Mechanics and Engineering，2006，195(50):6891-6908.