柔性元件對同振式矢量水聽器接收性能影響研究*

謝 攀 張 愷

(海軍工程大學兵器系 武漢 430033)

?

柔性元件對同振式矢量水聽器接收性能影響研究*

謝 攀 張 愷

(海軍工程大學兵器系 武漢 430033)

建立了同振球型矢量水聽器的物理模型,利用該模型研究了柔性元件對水聽器工作頻率、振速幅值和相移等性能參數的影響規律。結果表明:水聽器尺寸一定時,柔性元件彈性系數越小,水聽器下限工作頻率越低,一般在零點幾到幾赫茲之間;柔性元件主要影響低頻段振速幅值測量,且彈性系數越大,影響越大,而振速測量過程中由柔性元件引起的相移幾乎為零,可忽略不計。

同振式矢量水聽器; 柔性元件; 下限工作頻率; 振速幅值; 相移

Class Number TP212

1 引言

矢量水聽器是由聲壓水聽器和質點振速水聽器復合而成的能同時測量聲壓信息和質點振速信息的新型水聽器[1～3]。其低頻指向性好,空間增益高[4],較傳統聲壓水聽器及其基陣體積更小,可設計為水下小尺度平臺聲學探測裝置。根據工作原理的不同,矢量水聽器可分為壓差式矢量水聽器和同振式矢量水聽器,其中,同振式矢量水聽器能夠直接測量聲場中的質點振速,本身不產生明顯的聲場畸變,可以視為點接收器,而且性能參數穩定,在民用和軍事領域都有著廣泛的應用前景。

同振式矢量水聽器一般由內置傳感器、外殼、與外殼連接的柔性元件組成,其中柔性元件通常采用橡皮繩或彈簧。實際工程應用中,同振式矢量水聽器通過柔性元件懸置于大質量框架上,從而能有效隔離平臺振動對矢量水聽器的影響,保證水聽器的時間平均位置[5～6]。國內外對同振式矢量水聽器的研究主要集中于內置傳感器設計與改進上,對于外圍柔性元件的研究較少。而作為矢量水聽器中的關鍵元件,其結構參數直接影響矢量水聽器的接收性能,因此,為了更好地掌握柔性元件對矢量水聽器接收性能的影響,本文以同振式矢量水聽器為研究對象,通過建立相應的力學模型和等效電路模型,分析柔性元件對工作頻率,振速幅值和相移等性能參數的影響,為其中柔性元件設計提供理論依據。

2 振動模型分析

目前國內外常用的矢量水聽器的懸掛方式有兩根柔性元件垂直懸掛、六根柔性元件互相垂直懸掛、八根柔性元件垂直懸掛和八根柔性元件傾斜懸掛[7]。本文考慮將同振球型矢量水聽器通過六根互相垂直的彈性系數為K的彈簧懸置于大質量框架上。如圖1所示,柔性元件的初始長度為l0,水聽器固定于原點O時柔性元件被拉伸變為l,此時各柔性元件的變形量均為Δl=l-l0。

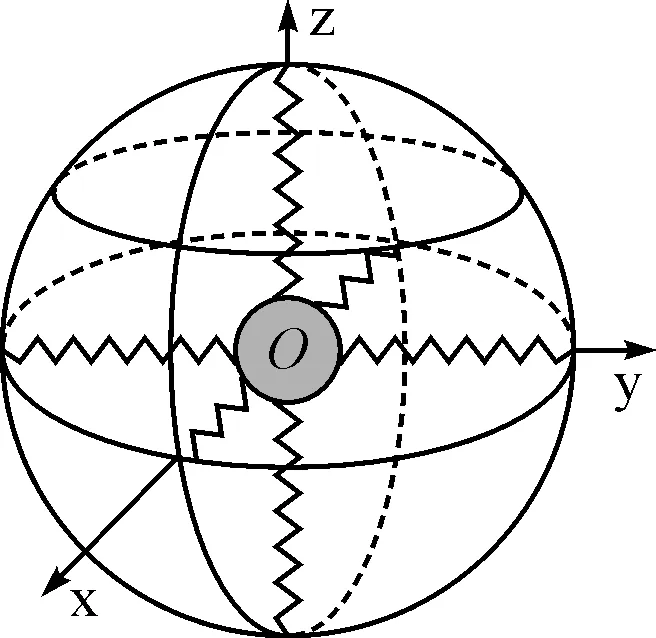
圖1 同振球型矢量水聽器懸置示意圖

圖2 同振球型矢量水聽器振動示意圖

為便于討論,本文根據同振球型矢量水聽器的工作原理以及懸掛系統的特性,假設:水聽器的外形尺寸遠遠小于聲波波長,幾何中心與重心重合,且平均密度等于水介質的密度;平面聲波在XOY平面內入射到水聽器上,水聽器在入射方向上以原點為中心做微幅振動,不做旋轉運動,且只考慮柔性元件的縱向拉伸力,而忽略其他方向作用力。圖2所示即為矢量水聽器的振動示意圖,它的動力學模型可以表示為一個單自由度的球體—柔性元件振動系統。為了直觀地表示矢量水聽器的受力情況,采用等效電路法分析此系統的動力學特性。

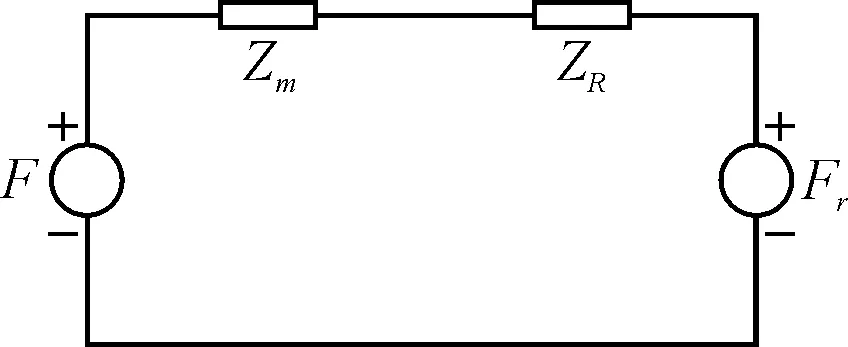
圖3 矢量水聽器等效電路模型

如圖3所示,F為聲壓作用于球體表面的作用力,Fr為柔性元件在外界刺激作用下對水聽器的總作用力,Zm和ZR分別表示自由球體在水中運動時的機械阻抗和輻射阻抗。

由聲學理論知識可知[8]:

(1)

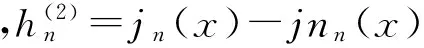
由文獻[9]可知作用力Fr為

Fr=j·2K(3-2l0/l)·Vc/ω

(2)

由于l0及l已知,所以當柔性元件彈性系數K一定時,Fr只與水聽器的振速幅值Vc和入射聲波角頻率ω有關。

耳聾分為神經性、傳導性和混合性三類，神經性耳聾是因感音神經出現障礙；傳導性耳聾是因內耳有炎癥，有積水；混合性耳聾是上面兩種因素交叉引起的。如果發現老人聽力下降，可進行純音測聽、聲導抗和耳聲發射等檢查，然后對癥下藥。

Zm,ZR分別為[10]

(3)

式中,M為矢量水聽器的質量,ρ水為水介質密度,c水為水中聲波傳播速度。

故矢量水聽器和柔性元件組成的球體—柔性元件振動系統總機械阻抗為[11]

(4)

當系統的總機械阻抗的虛部為零時,系統發生諧振,由此可求得此系統的諧振頻率為

(5)

當接收面在聲波作用下產生振動時,作用在接收器表面的作用力F與其接收面的實際振速幅值Vc之間的關系為:Vc=F/Z總。又入射聲波在球心處的質點振速為vw(t)=Vwejωt=(p0/ρ0c水)ejωt,故結合式(4)可得水聽器振速幅值與水質點的振速幅值比為

(6)

相位角φ為

(7)

其中E=2K(3-2l0/l)/ω2,它是一個與柔性元件彈性系數K及聲波頻率ω有關的參數。

在矢量水聽器實際使用過程中,內置傳感器的諧振頻率控制著矢量水聽器的上限工作頻率,而球體柔性元件振動系統的諧振頻率決定著矢量水聽器工作頻率的下限。由式(5)、式(6)可知:柔性元件對矢量水聽器接收性能的影響主要體現在兩個方面:一是水聽器工作頻率的下限,二是水聽器對質點振速的測量。

3 結果與分析

取l0=0.20m、l=0.25m,由式(5)可知矢量水聽器下限工作頻率f為

(8)

分別計算不同直徑水聽器的下限工作頻率f隨柔性元件彈性系數K的變化規律,結果見圖4。由計算結果可知:當柔性元件

3.2 柔性元件對振速測量的影響

取水聽器球體半徑a=0.04m,l0=0.20m、l=0.25m,分析柔性元件對水聽器所測振速幅值和相位的影響規律,結果見圖5。計算結果表明:柔性元件對矢量水聽器振速幅值測量的影響主要表現在低頻段,且柔性元件的彈性系數K值越大,影響越大;而振速測量過程中由柔性元件引起的相移幾乎為零,可忽略不計。

4 結語

本文以同振式矢量水聽器工作原理及懸掛系統基本要求為基礎,通過分析同振球型矢量水聽器水下振動的物理模型及等效電路模型,研究了柔性元件對同振式矢量水聽器接收性能的影響。研究結果表明: 1) 柔性元件對矢量水聽器接收性能的影響主要體現在兩個方面:一是水聽器工作頻率的下限,二是水聽器對質點振速的測量; 2) 水聽器尺寸一定時,柔性元件彈性系數越小,水聽器下限工作頻率越低,一般在零點幾赫茲到幾赫茲的范圍內; 3) 柔性元件對振速幅值測量的影響主要表現在低頻段,且柔性元件的彈性系數越大,影響越大; 4) 振速測量過程中由柔性元件引起的相移幾乎為零,可忽略不計。

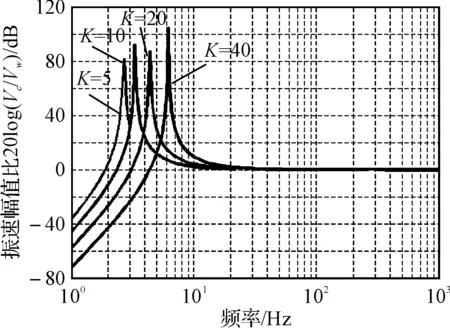
圖5 柔性元件對矢量水聽器振速測量的影響

[1] 孫貴青,李啟虎.聲矢量傳感器研究進展[J].聲學學報,2004,29(6):481-490.

[2] 孫貴青.矢量水聽器檢測技術研究[D].哈爾濱:哈爾濱工程大學,2001.

[3] Leslie C B, Kendall J M, Jones J L. Hydrophone for measuring particle velocity[J]. J. Acoust. Soc. Am,1956,28:711-715.

[4] 楊德森,洪連進.矢量水聽器原理及應用引論[M].北京:科學出版社,2009:1-2.

[5] Kim K. Investigation of an underwater acoustic vector sensor[D]. Pennsylvania: The Pennsylvania state University,2002.

[6] 賈志富.三維同振型矢量水聽器的特性及其結構設計[J].應用聲學,2001,20(4):15-20.

[7] 張俊.潛標平臺下的矢量水聽器懸掛系統聲學性能影響研究[D].哈爾濱:哈爾濱工程大學,2012.

[8] 何祚鏞,趙玉芳.聲學理論基礎[M].北京:國防工業出版社,1981.

[9] 時勝國.矢量水聽器及其在平臺上的應用研究[D].哈爾濱:哈爾濱工程大學,2006.

[10] Morse P, Ingard U. Theoretical Acoustics[M]. Princeton: Princeton University Press,1968:128.

[11] 時勝國,楊徳森.彈性元件對同振型振速水聽器的影響[J].應用聲學,2004,23(5):21-26.

Effect of Flexible Element on Receiving Performance of Co-vibrating Vector Hydrophone

XIE Pan ZHANG Kai

(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033)

A physical model of the vibrating sphere type vector hydrophone is established, and the flexible components influence on hydrophone frequency, vibration amplitude and phase shift performance parameters are studied by the model. The results show that when the hydrophone size is certain, the smaller elasticity of the flexible member, the lower limit on hydrophone lower working frequency, generally between a few tenths to a few hertz. Flexible components mainly affects the low frequency vibration velocity amplitude measurement, and the elastic coefficient is big, the greater the influence, and the phase shift caused by the flexible components in the process of velocity measuring is almost zero, negligible.

co-vibrating vector hydrophone, flexible components, lower working frequency, vibration amplitude, phase shift

2014年10月12日,

2014年11月29日

謝攀,男,碩士研究生,研究方向:武器系統運用與保障工程。張愷,男,博士研究生,研究方向:武器系統運用與保障工程。

TP212

10.3969/j.issn1672-9730.2015.04.038