一種基于線性近似的非線性系統(tǒng)模型預(yù)測(cè)控制方法*

蓋俊峰 趙國(guó)榮 周大旺

海軍航空工程學(xué)院，煙臺(tái)264001

模型預(yù)測(cè)控制(Model Predictive Control，MPC)是近年來(lái)崛起的一種成功的控制策略。MPC針對(duì)的是有優(yōu)化需求的控制問(wèn)題［1］，通過(guò)對(duì)某一性能指標(biāo)的最優(yōu)化來(lái)確定未來(lái)的控制作用［2］。由于現(xiàn)代工業(yè)生產(chǎn)過(guò)程的控制對(duì)象大多具有非線性特征，非線性系統(tǒng)的模型預(yù)測(cè)控制已成為當(dāng)前的研究熱點(diǎn)。而非線性系統(tǒng)預(yù)測(cè)控制的關(guān)鍵問(wèn)題在于如何處理非線性和降低在線計(jì)算量［1］。

非線性系統(tǒng)的設(shè)計(jì)和分析往往比線性系統(tǒng)困難得多，非線性微分方程通常不可能得到封閉形式的解析解，除非經(jīng)過(guò)特殊處理，而傅里葉變換、拉普拉斯變換和疊加原理等適用于線性系統(tǒng)的強(qiáng)有力的數(shù)學(xué)工具都不再適用于非線性系統(tǒng)的控制問(wèn)題。因此，對(duì)于實(shí)際工程操作人員來(lái)說(shuō)，最簡(jiǎn)單的方法就是把非線性動(dòng)態(tài)特性線性化，然后再用成熟的線性系統(tǒng)設(shè)計(jì)方法完成對(duì)控制系統(tǒng)的分析和綜合［3］。

文獻(xiàn)［4］用中值定理將非線性系統(tǒng)進(jìn)行線性化處理，用三次樣條函數(shù)來(lái)逼近線性系統(tǒng)的時(shí)變參數(shù)，并對(duì)樣條函數(shù)的常值參數(shù)進(jìn)行了辨識(shí);文獻(xiàn)［5］針對(duì)只含輸出非線性環(huán)節(jié)的系統(tǒng)沿期望的輸出軌跡用Taylor級(jí)數(shù)一階展開(kāi)近似線性化，但是該方法不能處理含有輸入非線性環(huán)節(jié)的系統(tǒng)。運(yùn)用Taylor級(jí)數(shù)展開(kāi)法對(duì)非線性系統(tǒng)進(jìn)行線性近似時(shí)，要求表征系統(tǒng)模型的輸入輸出函數(shù)必須連續(xù)可導(dǎo)，但有些物理系統(tǒng)并不滿(mǎn)足這一假設(shè)，因此Taylor級(jí)數(shù)展開(kāi)法對(duì)此不再適用。文獻(xiàn)［6］指出，利用Stirling插值公式對(duì)非線性函數(shù)進(jìn)行線性化處理的精度要高于Taylor一階近似，且不需對(duì)其進(jìn)行求導(dǎo)運(yùn)算，因此對(duì)不滿(mǎn)足連續(xù)可導(dǎo)假設(shè)的非線性系統(tǒng)，Stirling插值公式依然適用。

本文受文獻(xiàn)［6］的啟發(fā)，針對(duì)一類(lèi)非線性系統(tǒng)(尤其是系統(tǒng)模型的輸入輸出函數(shù)不滿(mǎn)足連續(xù)可導(dǎo)條件的非線性系統(tǒng))設(shè)計(jì)了一種基于線性近似的MPC方案。首先運(yùn)用Stirling插值公式對(duì)非線性函數(shù)進(jìn)行線性近似處理，并將模型預(yù)測(cè)控制性能指標(biāo)重構(gòu)為一個(gè)二次型最優(yōu)化問(wèn)題。最后，通過(guò)對(duì)二次型最優(yōu)化問(wèn)題的求解得到了模型預(yù)測(cè)控制的最優(yōu)控制序列。為了減少計(jì)算量，忽略了線性近似過(guò)程中產(chǎn)生的非線性高階項(xiàng)。仿真結(jié)果表明，該方案能達(dá)到滿(mǎn)意的控制效果，且具有降低控制能量消耗和縮短控制時(shí)間的優(yōu)點(diǎn)。

1 系統(tǒng)模型與問(wèn)題描述

考慮如下的非線性離散系統(tǒng):

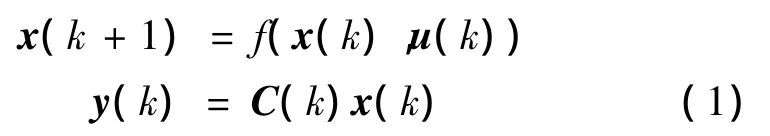
其中，x(k)∈Rn為狀態(tài)向量，u(k)∈Rm為控制輸入向量，y(k)∈Rp為輸出向量。f(·)為一連續(xù)的非線性函數(shù)，C(k)為一常數(shù)矩陣。

實(shí)際的工業(yè)過(guò)程中，受設(shè)備條件的限制，對(duì)系統(tǒng)的控制量和控制增量都有一定限制，需服從如下的約束條件:

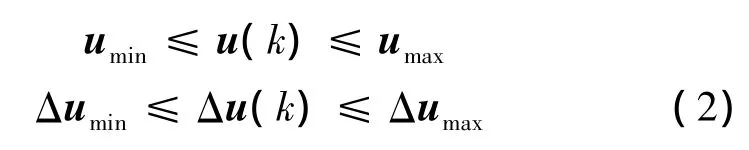
同時(shí)，為了避免系統(tǒng)輸出超過(guò)限制量，給出以下的輸出約束:

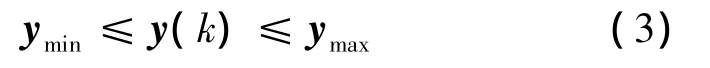
其中，umin≤umax，Δumin≤Δumax和ymin≤ymax分別為各向量的下界和上界。

模型預(yù)測(cè)控制是一種迭代最優(yōu)化方法:在每個(gè)采樣時(shí)刻k，測(cè)量或估計(jì)當(dāng)前狀態(tài)，然后通過(guò)對(duì)一個(gè)控制代價(jià)函數(shù)的最優(yōu)化來(lái)獲得最優(yōu)輸入向量。對(duì)模型(1)，給出以下滿(mǎn)足有限時(shí)域二次型規(guī)則的代價(jià)函數(shù):

2 系統(tǒng)的線性近似

當(dāng)非線性系統(tǒng)式(1)中的f(·)為一連續(xù)可微的非線性函數(shù)時(shí)，對(duì)于某些不太嚴(yán)重的非本質(zhì)非線性特性，用Taylor近似方法進(jìn)行分析和設(shè)計(jì)，在工作點(diǎn)的某一鄰域大體是正確的，產(chǎn)生的誤差也往往為工程上所接受。而當(dāng)f(·)為一不可微的非線性函數(shù)時(shí)，由于不能對(duì)其進(jìn)行求導(dǎo)運(yùn)算，Taylor近似方法在此不再適用。區(qū)別于Taylor級(jí)數(shù)展開(kāi)線性近似方法，用Stirling插值公式對(duì)非線性函數(shù)進(jìn)行線性近似時(shí)無(wú)需進(jìn)行求導(dǎo)運(yùn)算，只需用有限線性運(yùn)算來(lái)逼近該非線性函數(shù)［7-8］。由于Stirling插值公式能對(duì)余項(xiàng)直接進(jìn)行控制，這使得在某些應(yīng)用中其比Taylor近似更具吸引力。如果能選取合適的區(qū)間長(zhǎng)度，可以確保Stirling余項(xiàng)能接近完整Taylor級(jí)數(shù)的高階項(xiàng)［9］。鑒于上述優(yōu)點(diǎn)，本節(jié)采用Stirling插值公式法作為線性近似處理的數(shù)學(xué)工具。

下面用Stirling插值公式對(duì)非線性系統(tǒng)(1)進(jìn)行線性近似。首先定義如下函數(shù):

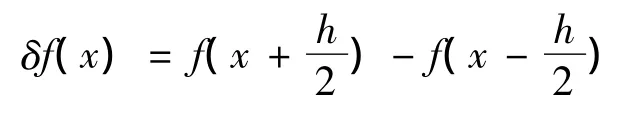
至此，當(dāng)非線性函數(shù)f()·不可微時(shí)，非線性系統(tǒng)式(1)可以通過(guò)Stirling插值公式法線性近似為如式(13)的形式。這種形式可為構(gòu)造二次型最優(yōu)化問(wèn)題提供方便，將在下節(jié)詳細(xì)說(shuō)明。

3 二次型最優(yōu)化問(wèn)題的重構(gòu)

此處，由于Q和R為正定陣，矩陣W也為正定陣，且所有的可行域都為凸的，因此最優(yōu)化問(wèn)題式(19)為一個(gè)凸二次規(guī)劃問(wèn)題。對(duì)二次規(guī)劃問(wèn)題式(19)求解，得到一個(gè)在控制域N上的控制增量向量Δˉu(k)，從而可計(jì)算出k時(shí)刻的最優(yōu)控制輸入。

4 仿真分析

本節(jié)選取某非線性對(duì)象系統(tǒng)，其非線性函數(shù)f(·)不滿(mǎn)足連續(xù)可微條件，Taylor級(jí)數(shù)展開(kāi)法不再適用于此處，故用Stirling插值公式法對(duì)其進(jìn)行線性近似處理。所選非線性對(duì)象系統(tǒng)描述如下:

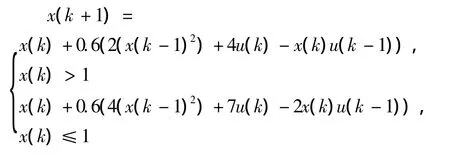
其中，預(yù)測(cè)域N=10，控制域Nu=3，控制時(shí)長(zhǎng)為t=100s。權(quán)值矩陣Q=2.5I，R=0.5I。輸入約束為 -35≤u(k)≤35，控制增量約束為 -40≤Δu(k)≤40，輸出約束為-10≤y(k)≤10。本例的參考輸出軌跡設(shè)置為一個(gè)方波信號(hào)。

本例對(duì)直接基于原非線性模型的情況和基于近似線性模型的情況分別進(jìn)行了仿真，結(jié)果如圖1～3所示。圖1中，Ref為參考輸出軌跡，y1為采用基于原非線性模型的MPC方案時(shí)系統(tǒng)的輸出軌跡，y2為采用基于本文近似線性模型的MPC方案時(shí)系統(tǒng)的輸出軌跡;圖2為2種不同情況下的控制輸入量曲線，其中u1為采用基于原非線性模型的MPC方案時(shí)的控制輸入，u2為采用基于本文近似線性模型的MPC方案時(shí)的控制輸入;圖3中，e1=y1-Ref，e2=y2-Ref，分別表示了采用2種MPC方案時(shí)的系統(tǒng)對(duì)參考輸出軌跡的跟蹤誤差。

仿真過(guò)程中，分別對(duì)2種方法進(jìn)行100步優(yōu)化計(jì)算所消耗的時(shí)間進(jìn)行統(tǒng)計(jì)求均值，可得到2種方法平均每步優(yōu)化計(jì)算所消耗的時(shí)間。

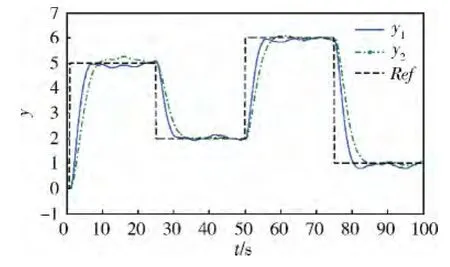
圖1 系統(tǒng)輸出跟蹤曲線

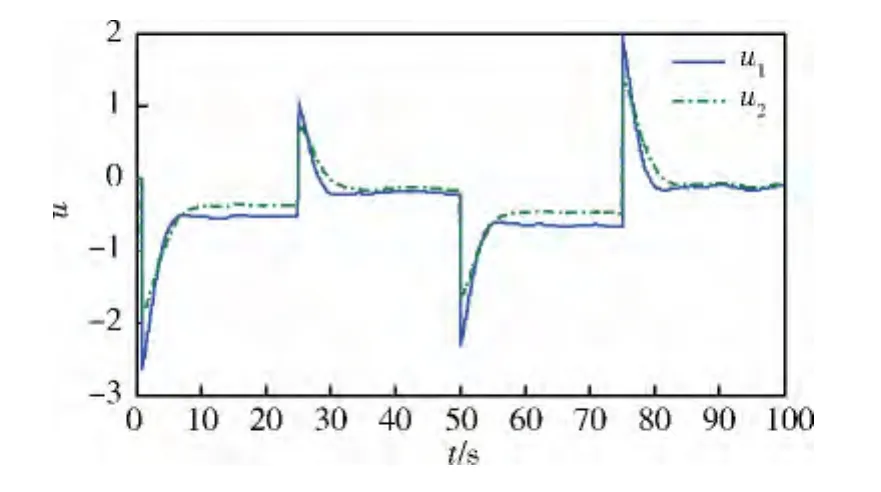
圖2 系統(tǒng)控制輸入曲線

經(jīng)計(jì)算，直接基于原非線性模型的MPC方案消耗時(shí)間為0.04672s;基于本文近似線性模型的MPC方案消耗時(shí)間為0.01925s。

由仿真結(jié)果可以看出，本文提出的方案跟蹤精度要比直接基于原非線性模型MPC方案的跟蹤精度略低。其原因是在對(duì)非線性模型進(jìn)行線性近似處理時(shí)，忽略了非線性高階項(xiàng)，這必然引入了線性化截?cái)嗾`差，使系統(tǒng)的跟蹤精度降低。但是，與直接基于原非線性模型的MPC方案相比，基于線性近似模型的MPC方案能減少控制能量的消耗，且大大節(jié)省了跟蹤時(shí)間。

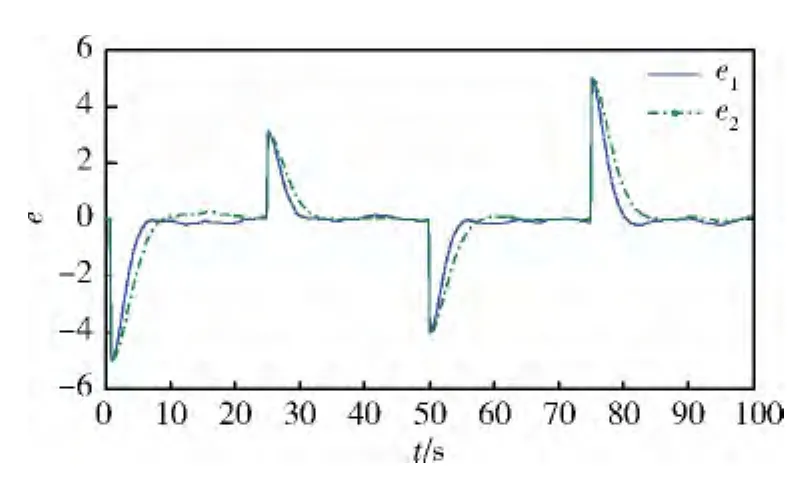
圖3 跟蹤誤差曲線

5 結(jié)論

提出了一種基于線性近似的非線性模型預(yù)測(cè)控制方法。首先運(yùn)用Stirling插值公式對(duì)非線性函數(shù)進(jìn)行線性近似處理，并將模型預(yù)測(cè)控制性能指標(biāo)重構(gòu)為一個(gè)二次型最優(yōu)化問(wèn)題。最后，通過(guò)對(duì)二次型最優(yōu)化問(wèn)題的求解得到了模型預(yù)測(cè)控制的最優(yōu)控制序列。為了降低計(jì)算的復(fù)雜度，該MPC方案忽略了線性近似過(guò)程中產(chǎn)生的非線性高階項(xiàng)。仿真結(jié)果表明，本文的MPC方案能達(dá)到較滿(mǎn)意的次優(yōu)控制效果，同時(shí)能降低控制能量的消耗，并且大幅縮短了控制時(shí)間。本文提出的方法僅為一種啟發(fā)性方法，在后續(xù)的工作中，需要對(duì)其穩(wěn)定性等作進(jìn)一步研究論證。

［1］ 席裕庚，李德偉，林姝.模型預(yù)測(cè)控制—現(xiàn)狀與挑戰(zhàn)［J］.自動(dòng)化學(xué)報(bào)，2013，39(3):222-232.(Xi Yugeng，Li Dewei，Lin Shu.Model predictive control-Status and challenges［J］.Acta Automatica Sinica，2013，39(3):222-232.)

［2］ 席裕庚.預(yù)測(cè)控制［M］.北京:國(guó)防工業(yè)出版社，1993.(XI Yugeng.Predictive Control［M］.Beijing:National Defence Industry Press，1993.)

［3］ 胡躍明，胡終須，毛宗源，李志權(quán).非線性控制系統(tǒng)的近似化方法［J］.控制理論與應(yīng)用，2001，18(2):160-165.(Hu Yueming，Hu Zhongxu，Mao Zongyuan，Li Zhiquan.Approximation methods of nonlinear control systems［J］.Control Theory and Applications，2001，18(2):160-165.)

［4］ 郭健，陳慶偉，朱瑞軍.一類(lèi)非線性系統(tǒng)的自適應(yīng)預(yù)測(cè)控制［J］.控制理論與應(yīng)用，2002，19(1):68-72.(Guo Jian，Chen Qingwei，Zhu Ruijun.Adaptive Predictive Control of a Class of Nonlinear System［J］.Control Theory and Applications，2002，19(1):68-72.)

［5］ Martin Rau，Dierk Schroder，Model predictive control with nonlinear state space models［C］.IEEE，AMC 2002-Maribor，Slovenia，2002，136～141.

［6］ 王亞鋒，孫富春，張友安，劉華平.一種跟蹤問(wèn)題中的次優(yōu)非線性預(yù)測(cè)控制算法［J］.控制與決策，2009，24(11)，1682-1686.(Wang Yafeng，Sun Fuchun，Zhang Youan，Liu Huaping.Suboptimal model predictive control for nonlinear system on tracking problem［J］.Control and Decision，2009，24(11):1682-1686.)

［7］ Magnus Norgaard，Niels K Poulsen and Ole Ravn［R］.Advances in Derivative-Free State Estimation for Nonlinear Systems，Technical report:IMM-REP-1998-15(revised edition)，Technical University of Denmark，Denmark，April 7，2000.

［8］ Schei T S.A finite difference method for linearization in nonlinear estimation algorithms［J］ .Automatica ，1997，33(11):2051-2058.

［9］ Magnus Norgaard，Niels K Poulsen and Ole Ravn.New developments in state estimation for nonlinear systems［J］.Automatica，2000，36(11):1627-1638.