海洋中深度與壓強(qiáng)的轉(zhuǎn)換方法

冀天宇，蔣國(guó)榮，史劍，周中剛，鄧波(.解放軍理工大學(xué)氣象海洋學(xué)院，江蘇南京0；.南京軍區(qū)氣象水文中心，江蘇南京0098; .解放軍98部隊(duì)，廣東湛江54000)

?

海洋中深度與壓強(qiáng)的轉(zhuǎn)換方法

冀天宇1，蔣國(guó)榮1，史劍1，周中剛2，鄧波3
(1.解放軍理工大學(xué)氣象海洋學(xué)院，江蘇南京211101；2.南京軍區(qū)氣象水文中心，江蘇南京210098; 3.解放軍91338部隊(duì)，廣東湛江524000)

摘要：介紹了海洋學(xué)計(jì)算中3種深度與壓強(qiáng)的轉(zhuǎn)化方法：（1）EOS-80（Equation of State of Seawater 1980，EOS-80）標(biāo)準(zhǔn)采用的方法；（2）最新發(fā)布的TEOS-10（Thermodynamics Equation of seawater 2010，TEOS-10）標(biāo)準(zhǔn)采用的方法；（3）通過(guò)海水吉布斯函數(shù)計(jì)算壓強(qiáng)與深度的關(guān)系的方法。對(duì)以上3種計(jì)算方法進(jìn)行了比較，結(jié)果表明：在一般的海洋學(xué)研究中，3種方法精度相差不大，均可使用。在要求計(jì)算效率的情況下，可以選用EOS-80標(biāo)準(zhǔn)采用的方法，在更高精度的海洋學(xué)研究中，應(yīng)該使用TEOS-10標(biāo)準(zhǔn)采用的方法或者吉布斯函數(shù)方法。

關(guān)鍵詞：深度壓強(qiáng)轉(zhuǎn)換；海水吉布斯函數(shù)；EOS-80；TEOS-10

1　引言

海洋中壓強(qiáng)與深度的換算關(guān)系是一種重要關(guān)系。在海洋調(diào)查儀器的觀測(cè)資料處理中，需要將海洋調(diào)查儀器測(cè)量得到的壓強(qiáng)轉(zhuǎn)化為深度；在海洋理論研究，海洋模式計(jì)算中，由于密度是壓強(qiáng)的函數(shù)，所以需要將等深度面上的格點(diǎn)資料中的深度值轉(zhuǎn)化為壓強(qiáng)值來(lái)計(jì)算密度。由于密度與壓強(qiáng)存在對(duì)應(yīng)的函數(shù)關(guān)系，所以對(duì)密度進(jìn)行鉛直向積分來(lái)計(jì)算壓強(qiáng)存在困難。壓強(qiáng)與深度的精確關(guān)系依賴(lài)于海水狀態(tài)方程的精確表達(dá)式。Saunder根據(jù)1980海水狀態(tài)方程（Equation of State of Seawater 1980，EOS-80），提出了一種實(shí)用的壓強(qiáng)與深度的轉(zhuǎn)換方法[1]，并且被EOS-80標(biāo)準(zhǔn)所采用[2]。但是這一方法忽略了溫度、鹽度對(duì)深度與壓強(qiáng)關(guān)系的影響。McDougall等根據(jù)最新提出的2010海水熱力學(xué)方程（Thermodynamics Equation of seawater 2010，TEOS-10）提出了壓強(qiáng)與深度轉(zhuǎn)換的一種新方法[3]，相比EOS-80標(biāo)準(zhǔn)而言包括了溫度、鹽度對(duì)壓強(qiáng)與深度的關(guān)系的影響，并被TEOS-10標(biāo)準(zhǔn)所采用[4]。鑒于目前探討海洋中深度與壓強(qiáng)的轉(zhuǎn)換關(guān)系的中文文獻(xiàn)較少，本文對(duì)上述計(jì)算方法進(jìn)行了介紹，并且在McDougall等工作的基礎(chǔ)上，根據(jù)海水熱力學(xué)定律[5]，依據(jù)海水吉布斯函數(shù)，實(shí)現(xiàn)了壓強(qiáng)轉(zhuǎn)換為深度的吉布斯函數(shù)方法，并對(duì)以上三種計(jì)算方法進(jìn)行了比較和討論。

2　EOS-80采用的壓強(qiáng)與深度的轉(zhuǎn)換關(guān)系

2.1從深度到壓強(qiáng)的轉(zhuǎn)換

Saunders[1]給出了根據(jù)1980海水狀態(tài)方程給出的實(shí)用的溫度壓強(qiáng)關(guān)系：

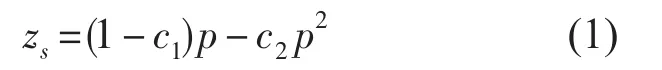
式中，c1=(5.92+5.25sin2?)×10-3[mdb-1]，c2= 2.21×10-6mdb-2。

根據(jù)（1）式得到（2）式，即為EOS-80標(biāo)準(zhǔn)采用的深度到壓強(qiáng)的標(biāo)準(zhǔn)算法：

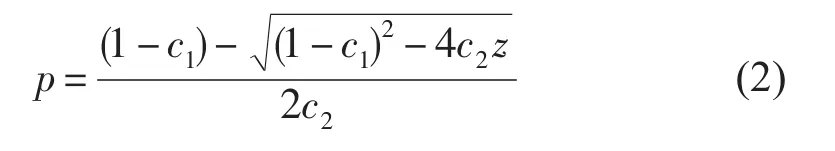
2.2從壓強(qiáng)到深度的轉(zhuǎn)換

EOS-80標(biāo)準(zhǔn)對(duì)從壓強(qiáng)到深度的轉(zhuǎn)換采取了擬合的方法，即

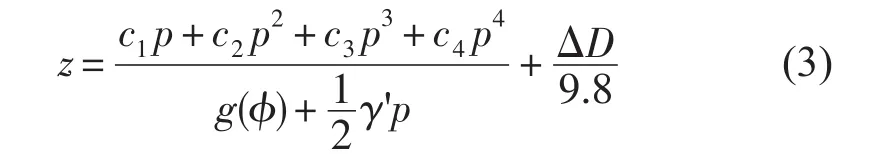
式中，c1=9.72659，c2=-2.2512×10-5，c3= -2.279×10-10,c4=-1.82×10-15,γ'=2.184×10-6ms-2/ db，ΔD=∫p0δdp'，δ=ν(S,T,P)-ν(35,0,P)，為比容偏差，g(?)=9.780318(1.0+5.2788×10-3sin2(?)+10-5× sin4(?))[ms-2]。

（3）式中的比容偏差項(xiàng)要比第一項(xiàng)小兩個(gè)量級(jí)[1]，這說(shuō)明在深度與壓強(qiáng)的關(guān)系中，溫度與鹽度的貢獻(xiàn)很小。EOS-80方法在壓強(qiáng)轉(zhuǎn)換為深度時(shí)略去了上式中的比容偏差項(xiàng)，一般而言這是可以接受的，但是在高精度的海洋學(xué)研究中，直接略去比容偏差項(xiàng)對(duì)深度與壓強(qiáng)的關(guān)系的影響，勢(shì)必會(huì)造成一定的誤差。

3　TEOS-10采用的壓強(qiáng)與深度的轉(zhuǎn)換關(guān)系

TEOS-10是在一個(gè)完善的理論體系中建立起來(lái)的具有一致性和完備性的新方程，參考聯(lián)合國(guó)教科文組織（United Nations Educational，Scientific，and Cultural Organization，UNESCO）對(duì)該方程的官方說(shuō)明，TEOS-10方法在進(jìn)行深度與壓強(qiáng)關(guān)系的轉(zhuǎn)換時(shí)，采用類(lèi)似EOS-80方法的做法，首先對(duì)靜力平衡方程=-ρg進(jìn)行垂直積分，得到：

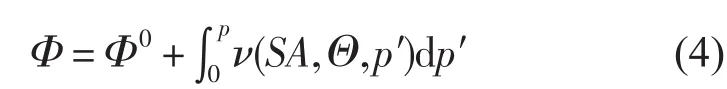
式中，Φ代表重力位勢(shì)，SA代表絕對(duì)鹽度，Θ代表守恒溫度（絕對(duì)鹽度、守恒溫度的定義、同實(shí)用鹽度和攝氏溫度的轉(zhuǎn)化參考UNESCO對(duì)TEOS-10的官方說(shuō)明[4])。

Feistel和Hagen（1995）導(dǎo)出了海水的吉布斯函數(shù)[6]，可以用來(lái)求解包括內(nèi)能，熵，比容，聲速，位溫等一些熱力學(xué)變量。Mcdougall對(duì)該吉布斯函數(shù)進(jìn)行了擬合，提出了包含25項(xiàng)的計(jì)算海水密度的表達(dá)式，并且被TEOS-10標(biāo)準(zhǔn)所采用[7]。該密度的擬合表達(dá)式能夠直接對(duì)比容進(jìn)行積分，從而直接求解出海水的比焓。與EOS-80標(biāo)準(zhǔn)中采用的方法不同，該方法在計(jì)算比容的鉛直積分時(shí)沒(méi)有略去比容偏差的貢獻(xiàn)。這樣，溫度、鹽度對(duì)深度與壓強(qiáng)的關(guān)系的影響就包括在了表達(dá)式中。對(duì)（4）式進(jìn)行積分后有：

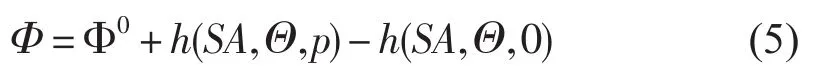
式中，h(SA,Θ,p)代表海水的比焓，Φ代表海水重力勢(shì)。根據(jù)Mcdougall擬合的25項(xiàng)密度計(jì)算公式可以直接求得海水的比焓[4]，即h(SA,Θ,p)，進(jìn)而得到深度與壓強(qiáng)的關(guān)系。

在進(jìn)行從深度到壓強(qiáng)的轉(zhuǎn)換時(shí)，TEOS-10方法根據(jù)上述從壓強(qiáng)到深度的轉(zhuǎn)換關(guān)系，采用Mcdougall等提出的改進(jìn)的Newton-Raphson迭代方法[8]求解從深度到壓強(qiáng)的轉(zhuǎn)換關(guān)系，其本質(zhì)上的原理同樣是Mcdougall等擬合出的，用于計(jì)算密度的25項(xiàng)表達(dá)式。

4　根據(jù)海水的吉布斯函數(shù)計(jì)算深度與壓強(qiáng)的關(guān)系

TEOS-10相對(duì)于EOS-80最大的區(qū)別就是利用海水的吉布斯函數(shù)計(jì)算海水的各種性質(zhì)。熱力學(xué)理論現(xiàn)在已經(jīng)證明：如果一個(gè)熱力學(xué)系統(tǒng)基本方程是已知的，那么通過(guò)相應(yīng)的微分和代數(shù)運(yùn)算就能夠求出整個(gè)系統(tǒng)的各種熱力學(xué)性質(zhì)。目前雖然沒(méi)法直接計(jì)算得到海水的吉布斯函數(shù)，但是可以分別求解出海水中水和鹽的吉布斯函數(shù)[5]。

首先定義比吉布斯能函數(shù)g，表示單位質(zhì)量海水的吉布斯能。其與海水的質(zhì)量無(wú)關(guān)。海水的比吉布斯能可以視為海水中純水的比吉布斯能和鹽的比吉布斯能之和，即：

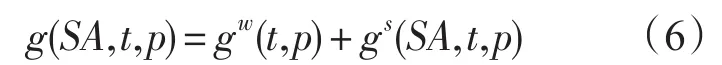
ν表示比容。根據(jù)熱力學(xué)關(guān)系：

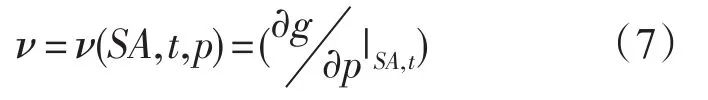
可以求得比容對(duì)壓強(qiáng)的積分為：

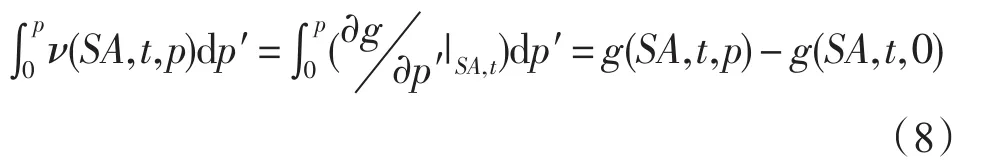
積分形式的海水靜力平衡方程為:

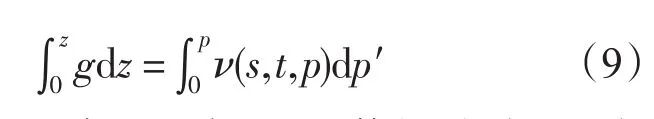
式中，ν表示比容。根據(jù)1979修訂公式，重力加速度隨著緯度和深度變化，即g=gs+γz，gs代表重力加速的地球表面值，是緯度的函數(shù)。gs與緯度的關(guān)系由下式給出：

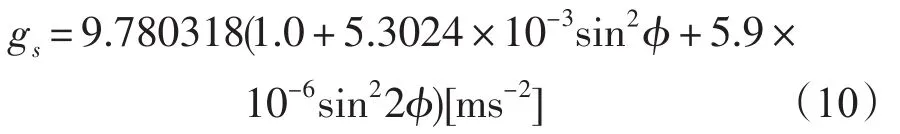
帶入（9），得到：

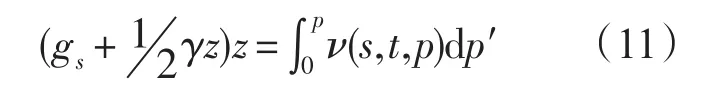
引入壓強(qiáng)修正項(xiàng)（Saunders，1981），根據(jù)SA與S的轉(zhuǎn)化關(guān)系：

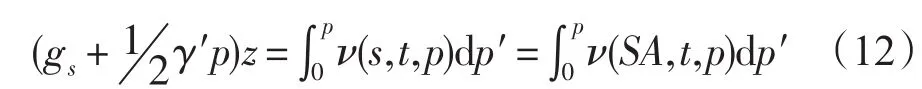
式中，γ′=2.226×10-6ms-2/db。

根據(jù)（8）和（11）式可以得到壓強(qiáng)、深度的轉(zhuǎn)化關(guān)系：

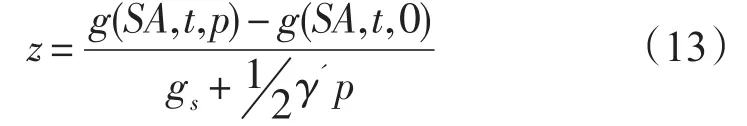
式中，海水的吉布斯函數(shù)g為多項(xiàng)式的形式，其系數(shù)可以參考UNESCO發(fā)布的TEOS-10官方使用手冊(cè)[4]。

由于壓強(qiáng)變量是海水的吉布斯函數(shù)的一個(gè)自變量，在求解從深度到壓強(qiáng)的關(guān)系便會(huì)遇到困難。因此吉布斯函數(shù)方法只適于求解從壓強(qiáng)到深度的換算關(guān)系。

5　計(jì)算結(jié)果的對(duì)比和討論

海洋研究中常用簡(jiǎn)單的線性關(guān)系進(jìn)行壓強(qiáng)與深度之間的換算，即：

式中，p0為標(biāo)準(zhǔn)大氣壓，ρref為參考密度，取為1025 kg/m3。為了說(shuō)明每種方法的計(jì)算精度，本文根據(jù)WOA09（World Ocean Atlas 2009）氣候態(tài)平均資料，選取分別選取太平洋，印度洋，大西洋中的三個(gè)站點(diǎn)，其經(jīng)緯度坐標(biāo)分別為（173.5°E，30.5°N），（29.5°W，26.5°N），（75.5°E，15.5°S）。所選站點(diǎn)的溫鹽垂直分布曲線見(jiàn)圖1。表1至表4列出了不同方法的計(jì)算結(jié)果。

圖1　所選擇站點(diǎn)的溫度、鹽度垂直分布

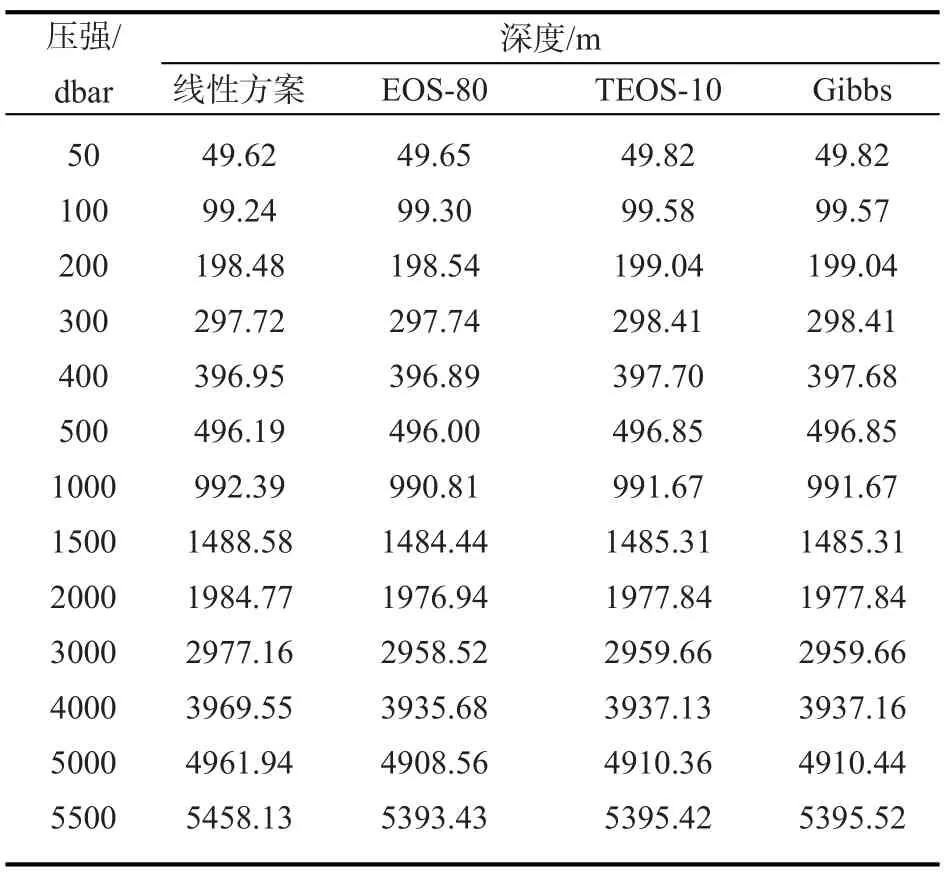
表1　太平洋中部站點(diǎn)壓強(qiáng)轉(zhuǎn)化為深度的結(jié)果的比較

表1、表2的第一列是常用的深度與壓強(qiáng)的線性關(guān)系的計(jì)算結(jié)果，比較幾種不同方法的計(jì)算結(jié)果，可以看出采取線性關(guān)系計(jì)算海洋中的壓強(qiáng)與深度關(guān)系與其他方法相比還是存在比較大的差異的，這種差異在海洋表層較小，隨著深度的增加而增加，最大差值能夠達(dá)到7%。鑒于公式（1）的簡(jiǎn)潔性，完全可以采用EOS-80標(biāo)準(zhǔn)使用的方法來(lái)估算海洋中深度與壓強(qiáng)的關(guān)系。

表1的第三四列表示在所取站點(diǎn)的溫鹽分布的情況下，不同壓強(qiáng)條件，TEOS-10標(biāo)準(zhǔn)采用的計(jì)算方法和吉布斯函數(shù)計(jì)算方法計(jì)算結(jié)果的差值（其余站點(diǎn)結(jié)果相似，未列出）。兩種方法的計(jì)算原理同屬于熱力學(xué)框架。從表1中可以看出，在小于2000 db的壓強(qiáng)條件下，這兩種方法的計(jì)算結(jié)果幾乎完全一致，隨著深度的增加，一直5500 db的深度，二者的計(jì)算差值僅為0.2 m左右，因此可以說(shuō)明根據(jù)吉布斯函數(shù)的計(jì)算壓強(qiáng)到深度的轉(zhuǎn)換關(guān)系的方法是可行的，適用的。

表3和表4分別表示使用EOS-80方法和TEOS-10方法進(jìn)行深度與壓強(qiáng)轉(zhuǎn)換的計(jì)算結(jié)果的差值。從壓強(qiáng)轉(zhuǎn)換為深度的結(jié)果來(lái)看（見(jiàn)表3），這兩種方法的差值最大為2 m左右。從深度轉(zhuǎn)化為壓強(qiáng)的結(jié)果來(lái)看（見(jiàn)表4），這兩種方法計(jì)算差值最大為150 db左右，但是在海洋中上層，這兩種方法的計(jì)算差異比較小。因此在不同的計(jì)算精度要求下，尤其是在將深度轉(zhuǎn)為壓強(qiáng)的計(jì)算中，兩種方法的計(jì)算差異還是要考慮的。

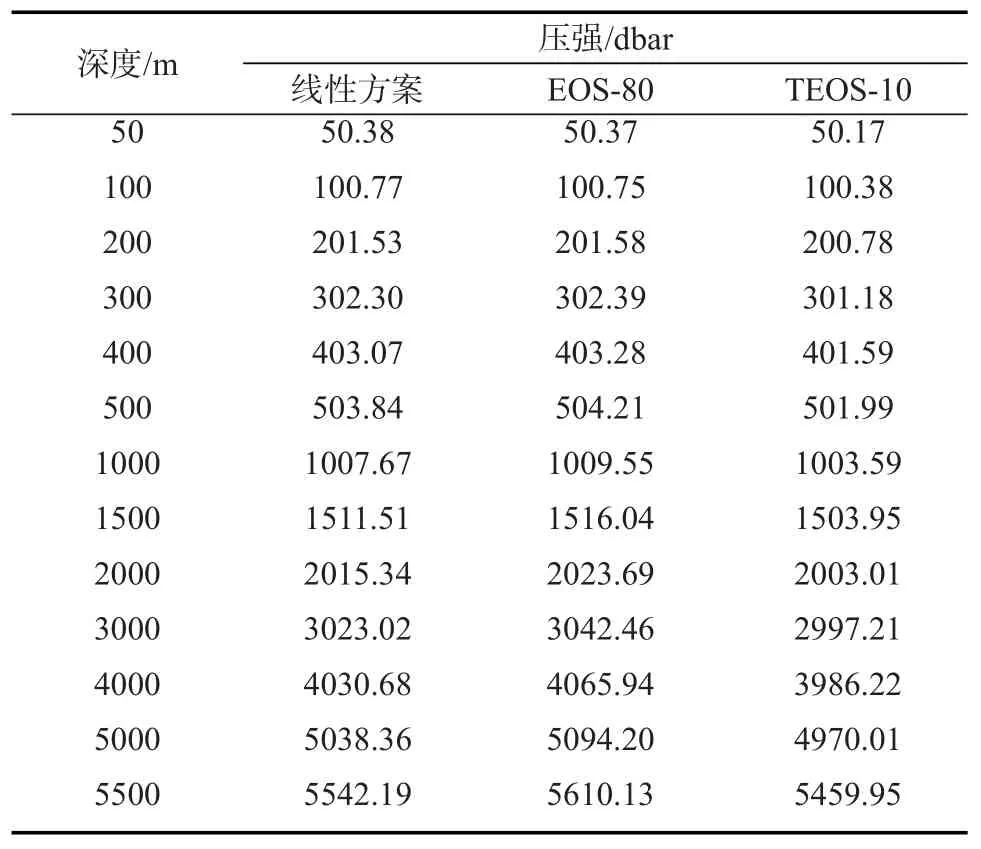
表2　太平洋中部站點(diǎn)深度轉(zhuǎn)化為壓強(qiáng)的結(jié)果的比較

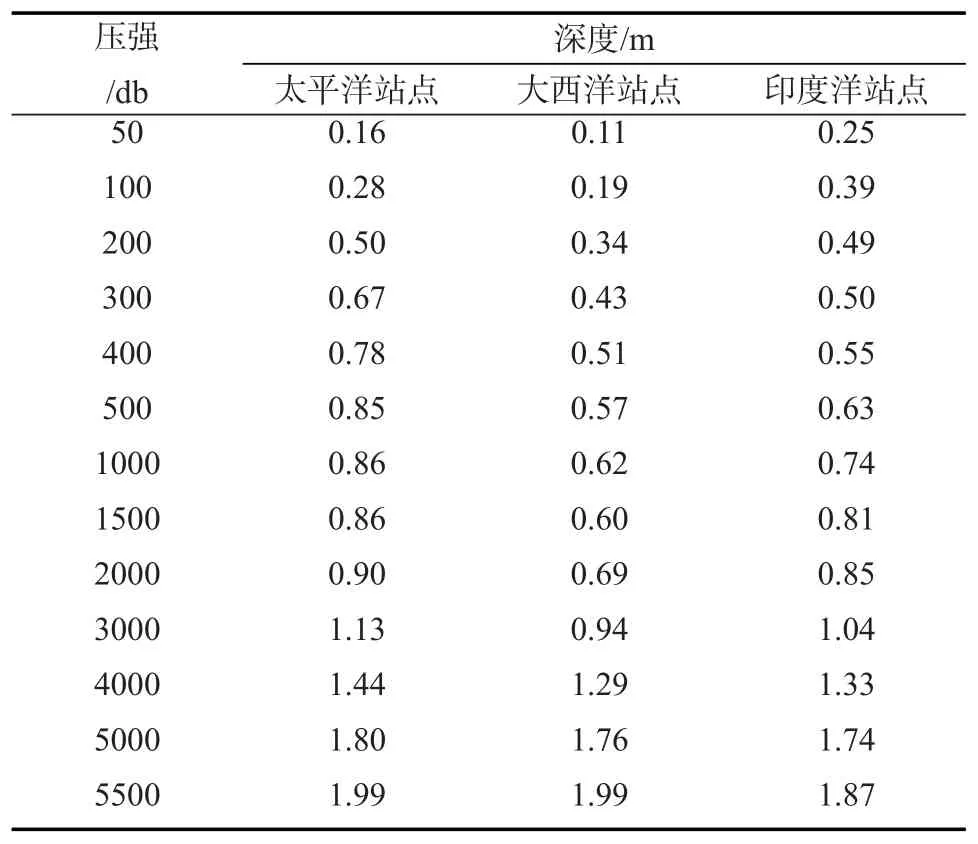
表3　三個(gè)站點(diǎn)上使用TEOS-10方法和EOS-80方法將壓強(qiáng)轉(zhuǎn)化為深度的結(jié)果的差值

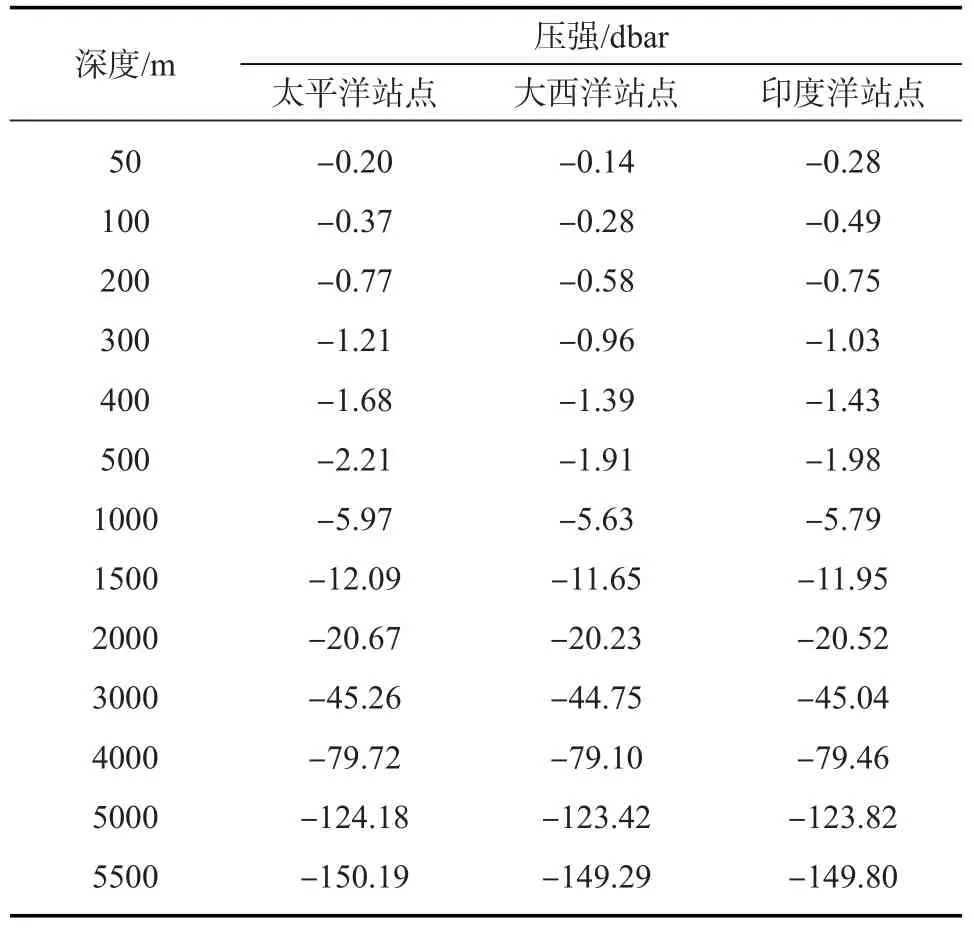
表4　三個(gè)站點(diǎn)上使用TEOS-10方法和EOS-80方法將深度轉(zhuǎn)化為壓強(qiáng)的結(jié)果的差值

造成這兩種計(jì)算結(jié)果的差異的原因在于EOS-80方法計(jì)算深度與壓強(qiáng)的關(guān)系時(shí)略去了比容偏差項(xiàng)ΔD=∫0pδdp'（見(jiàn)公式3），從而建立了深度與壓強(qiáng)的直接關(guān)系。Saunder[1]計(jì)算后認(rèn)為比容偏差項(xiàng)對(duì)深度與壓強(qiáng)關(guān)系的影響比壓強(qiáng)的改變對(duì)深度與壓強(qiáng)關(guān)系的影響要小兩個(gè)量級(jí)，可以不予考慮。TEOS-10方法采用Mcdugall等根據(jù)海水吉布斯函數(shù)擬合出的25項(xiàng)表達(dá)式計(jì)算深度與壓強(qiáng)的關(guān)系，比容偏差項(xiàng)對(duì)深度壓強(qiáng)轉(zhuǎn)換關(guān)系的影響包括在比容對(duì)壓強(qiáng)的積分中（見(jiàn)公式5），從理論上而言，TEOS-10標(biāo)準(zhǔn)更為精確。使用吉布斯函數(shù)計(jì)算深度與壓強(qiáng)的關(guān)系同樣能夠?qū)⒈热萜铐?xiàng)的影響包含在比容對(duì)壓強(qiáng)的積分內(nèi)（見(jiàn)公式8）。從這一點(diǎn)上看，TEOS-10方法和吉布斯函數(shù)計(jì)算方法要比EOS-80的計(jì)算方法更為精確。比容偏差項(xiàng)是溫度、鹽度與壓強(qiáng)的函數(shù)。眾所周知，海洋中上層是溫度鹽度變化劇烈的水層，從表3、表4中可以看出，在不同站點(diǎn)的中上層，這兩種不同方法的計(jì)算差異還是比較小的。這是因?yàn)闇囟取Ⅺ}度的變化對(duì)比容偏差的影響較小。而隨著深度與壓強(qiáng)的增加，這兩種計(jì)算方法的差值也逐漸增加，這是因?yàn)閴簭?qiáng)的變化對(duì)比容偏差項(xiàng)影響較大，從而造成了表3表4所示的差異。

根據(jù)以上討論，對(duì)于一般的海洋學(xué)研究，采用EOS-80和TEOS-10方法均可，也可采用吉布斯函數(shù)方法。TEOS-10標(biāo)準(zhǔn)方法和吉布斯函數(shù)方法相對(duì)EOS-80標(biāo)準(zhǔn)方法而言，在將深度轉(zhuǎn)化為壓強(qiáng)時(shí)，計(jì)算精度有明顯提高，但同時(shí)計(jì)算過(guò)程也較復(fù)雜。在有些計(jì)算資源緊張的場(chǎng)合下（比如在嵌入式設(shè)備中），為了權(quán)衡計(jì)算精度和計(jì)算效率之間的矛盾，可以采用EOS-80標(biāo)準(zhǔn)所采用的方法。如果在精度要求更高的情況下，應(yīng)該采用TEOS-10標(biāo)準(zhǔn)使用的方法或者本文使用的吉布斯函數(shù)計(jì)算的方法。

6　結(jié)論

本文討論了三種深度與壓強(qiáng)相互轉(zhuǎn)化的方法，并比較了三者的差異。在一般的海洋學(xué)研究中，這三種方法均可以使用。在注重計(jì)算效率的情況下，可以使用EOS-80標(biāo)準(zhǔn)所使用的方法，在精度要求更高的海洋學(xué)研究中，應(yīng)該使用TEOS-10標(biāo)準(zhǔn)使用的計(jì)算方法，如果只需要將壓強(qiáng)轉(zhuǎn)換為深度，吉布斯函數(shù)計(jì)算方法也是可行的。

參考文獻(xiàn)：

[1] Saunders P M. Practical conversion of pressure to depth [J]. Journal of Physical Oceanography, 1981, 11: 573-57.

[2] ICES, SCOR, IAPSO. The Practical Salinity Scale 1978 and the International Equation of State of Seawater 1980 [R]. UNESCO Technical Papers in Marine Science No 36, 1981: 25.

[3] McDougall T J,Barker P M. Getting started with TEOS-10 and the Gibbs Seawater(GSW)Oceanographic Toolbox 2010 [ SCOR/ IAPSO WG127][R].2011.28.

[4] IOC, SCOR, IAPSO. The international thermodynamic equation of seawater-2010: Calculation and use of thermodynamic properties [J]. Intergovernmental Oceanographic Commission, Manuals and Guides, 2010, 56: 196.

[5] Sun Y M, Shi J X, Yang H P. The thermodynamic equation of seawater 2010 and its comparison with the equation of seawater 1980 [J].Advance in Earth Science, 2012, 27(9): 1014-1025.

[6] IAPWS. Release on the IAPWS Formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use[A].Fredericia,1996.

[7] Jackett D R, McDougall T J, Feistel R, et al. Algorithms for density, potential temperature, conservative temperature, and the freezing temperature of seawater [J]. Journal of Atmospheric and Oceanic Technology, 2006, 23: 1709-17128.

[8] McDougall T J, Wotherspoon S J. A simple modification of Newton’s method to achieve convergence of order 1 +√2 [J]. Applied Mathematics Letters, 2014, 29: 20-25.

[9]姚勇,衛(wèi)薇,陳華秋. 90國(guó)際溫標(biāo)對(duì)80國(guó)際海水狀態(tài)方程影響的研究[J].海洋技術(shù), 2001, 20(3): 74-78.

[10] Bacon S, Fofonoff N. Oceanic heat flux calculation [J]. Journal of Atmospheric and Oceanic Technology, 1996, 13(6): 1327-1329.

[11] Feistel R, Weinreben S, Wolf H, et al. Density and absolute salinity of the Baltic Sea 2006-2009[J]. Ocean Science, 2010, 6 (1): 3-24.

[12] Jackett D R, McDougall T J, Feistel R, et al. Algorithms for density, potential temperature, conservative temperature, and the freezing temperature of seawater[J]. Journal of Atmospheric and Oceanic Technology, 2006, 23(12): 1709-1728.

Conversion methods of depth and pressure in the ocean

JI Tian-yu1, JIANG Guo-rong1, SHI-Jian1, ZHOU Zhong-gang2, DENG Bo3
(1. Insititude of Meteorology, PLA univ. of Sci. & Tech., Nanjing 211101 China; 2. Mete-hydrological center of Nanjing Military Region, Nanjing 210016 China; 3. 91388 PLA troops, Zhanjiang 524000 China)

Abstract：Three conversion methods of depth and pressure in the ocean are described. (1) Method adopted by EOS-80 standard (Equation of State of Seawater 1980, EOS-80); (2) Method adopted by TEOS-10 standard (Thermodynamics Equation of seawater 2010，TEOS-10); (3) Convert pressure to depth via the Gibbs function of seawater. After comparison of three methods, the results show that, in general oceanographic research, the three methods can all be used in general oceanographic research, according to their similar accuracy. However, the EOS-80 method should be adopted in the request of computational efficiency, and the TEOS-10 method or Gibbs function method should be taken in the high-precision oceanographic research.

Key words：conversion between depth and pressure；Gibbs function；EOS-80；TEOS-10

作者簡(jiǎn)介：冀天宇（1989-），男，碩士研究生，主要研究方向?yàn)楹Ｑ髣?dòng)力學(xué)與數(shù)值模擬。E-mail：414203624@qq.com

基金項(xiàng)目：國(guó)家自然科學(xué)基金（41106014）；江蘇省自然科學(xué)基金（BK20131066）

收稿日期：2014-06-10

DOI:10.11737/j.issn.1003-0239.2015.02.007

中圖分類(lèi)號(hào)：P733

文獻(xiàn)標(biāo)識(shí)碼：A

文章編號(hào)：1003-0239（2015）02-0045-06