卡爾曼濾波抗積分飽和PDF控制系統研究

Research on Kalman Filtering Anti-integral Saturation PDF Control System

鄢華林　祁圣民

(江蘇科技大學機械工程學院，江蘇 鎮江　212003)

卡爾曼濾波抗積分飽和PDF控制系統研究

Research on Kalman Filtering Anti-integral Saturation PDF Control System

鄢華林祁圣民

(江蘇科技大學機械工程學院，江蘇 鎮江212003)

摘要：針對非接觸式登船梯控制系統在實際工作中不可避免地受到干擾信號的影響這一問題，提出了卡爾曼濾波抗積分飽和PDF控制系統。該控制系統主要由PDF控制器、抗積分飽和控制器和卡爾曼濾波器三個部分組成。卡爾曼濾波抗積分飽和PDF控制系統具有優良的控制性能和動態品質。該控制系統能快速跟蹤設定的參考信號且無超調與振蕩出現，同時能抑制白噪聲的污染。仿真結果表明，該控制系統提高了系統的自適應與魯棒性。

關鍵詞：偽微分控制PDF抗積分飽和卡爾曼濾波Matlab仿真

Abstract：In practical operation, the non-contact control system of boarding ladder is inevitably affected by interference signals, the design of Kalman filtering anti-integral saturation PDF control system is proposed. This control system mainly consists of three parts, i.e., PDF controller, anti-integral saturation controller and Kalman filter. This control system possesses excellent control performance and dynamic quality, it can fast track the reference signal without overshoot or oscillation, and white noise pollution can be restrained. The result of simulation indicates that the control system improves the robustness and adaptation of the system.

Keywords：Pseudo-differential controlPseudo-derivative feedback(PDF)Anti-integral saturationKalman filteringMatlab simulation

0引言

非接觸登船梯是一個復雜的多輸入多輸出非線性系統，使用常規的控制算法如PI和PID，實現上雖然非常簡單方便，但難以保證登船梯具有良好的動態和靜態品質。為了提高非接觸式登船梯跟蹤性能，采用抗積分飽和偽微分反饋控制(pseudo-derivative-feedback,PDF)算法。此算法自適應能力強，且對被控對象的數學模型精度要求不是很高，參數整定方便。

由于海上的工作環境比較惡劣，非接觸式登船梯工作中經常受到干擾信號的影響，導致其信號中常含有高頻干擾，使得控制品質下降。為了獲取需要的信號，需要對控制信號與反饋信號進行濾波處理。卡爾曼濾波作為一種重要的最優估計理論被廣泛應用于導航、控制、目標跟蹤等領域[1]。本文主要對存在控制過程噪聲與測量噪聲時的控制問題進行了研究。

1卡爾曼濾波抗積分飽和PDF算法

1.1　PDF算法簡介

PDF控制算法是微分反饋控制算法的改進算法，微分反饋算法在前向通道中只有積分運算，如果被控系統的階次為n，則整個控制系統將會變成(n+1)次。從穩定性與可控性的角度來考慮，對n階被控系統，必須提供被控變量的n階微分。在仿真試驗中微分的實現很容易，但是在工程上高階微分很難實現，而且微分作用會增強信號中的噪聲。為了降低微分對噪聲信號的放大，又不影響微分的功效，對微分反饋進行了改進，如圖1與圖2所示。

圖1　微分反饋控制算法

圖2　偽微分控制算法

從圖1可以看出，對于二階被控系統，輸出信號C的微分的積分仍然是C，所以沒有必要對C進行微分運算后再進行積分運算，且工程上應盡量避免微分運算。從圖2可以看出，M1(t)的值與圖1中是相同的，也就是兩種算法實際上在控制量的輸出上是等效的。

(1)

PDF控制算法實際微分比微分反饋算法要低一階，這樣既保證了良好的控制效果，又降低了微分對噪聲的放大，對控制品質的提高起到了很好的作用。

1.2　抗積分飽和

積分飽和是指系統存在一個方向的偏差，控制器輸出由于積分作用的不斷累積而加大，從而導致末級放大器(final control element,FCE)達到工作極限mmax。以液壓閥門為例，此時閥的開度最大，如圖3所示，這時如果輸入值u(k)繼續增大，閥門的開度不能再增大，控制器輸出的控制量超過末級放大器的正常運行范圍進入飽和區。當系統出現反向偏差時，控制量逐漸減小，進入飽和區的程度越深,退出時需要的時間越長，這時就會出現超調增大的現象，使控制性能惡化。

圖3　末級放大器工作示意圖

防止積分飽和的方法就是抗積分飽和。該方法的思路是監視控制器輸出的控制量，如果控制量超過了FCE的極限值mmax，則累加負偏差；如果超過了FCE的極限值-mmax，則累加正偏差。

在PDF算法中引入抗積分飽和可以擺脫FCE對PDF參數的限制，擴大參數的整定范圍，使得參數的整定更為方便。引入抗積分飽和后PDF算法在整定時只要滿足等極點原則即可。以二階被控對象(圖2)為例，參數整定為：

(2)

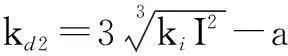
(3)

1.3　卡爾曼濾波

對于線性離散系統來說，離散狀態方程如下：

x(k)=Ax(k-1)+B[u(k)+w(k)]

(4)

yv(k)=Cx(k-1)+v(k)

(5)

式中：x(k)為k時刻的系統狀態；u(k)為k時刻對系統的控制量；A和B為系統參數，對于多模型系統，它們為矩陣，主要由被控對象的數學模型來決定；yv(k)為k時刻的測量值，這個測量值里包含有干擾噪聲；C為測量系統的參數，對于多測量系統，C為矩陣；w(k)和v(k)分別為過程噪聲和測量噪聲，它們被假設成高斯白噪聲，它們的協方差分別為Q、R。

首先，初始化X(k)以及X(k)對應的協方差P(k)，同時對Q、R進行初始化，初始化之后根據X(k)與P(k)的值計算卡爾曼增益Mn(k)。Mn(k)計算公式如下。

(6)

計算完卡爾曼增益之后，接下來計算的是X(k)對應的協方差P(k)，計算公式如下。

問題3：定理的逆命題,即“若函數y=f(x)在區間[a,b]上的圖象是一條不間斷的曲線,且函數y=f(x)在區間(a,b)上有零點,則f(a)·f(b)<0”成立嗎？

P(k|k-1)=AP(k-1|k-1)AT+BQBT

(7)

P(k)=[In-Mn(k)C]P(k|k-1)

(8)

式中：P(k-1|k-1)為X(k-1)狀態時對應的協方差；P(k)為X(k)狀態對應的協方差。

更新下一個狀態，即由X(k-1)來更新X(k)，更新公式如下。

x(k)=Ax(k-1)+Mn(k)[yv(k)-CAx(k-1)]

(9)

由更新的狀態X(k)來計算濾波過后的輸出值，輸出公式為：

ye(k)=Cx(k)

(10)

2系統結構及仿真

2.1　系統結構

基于卡爾曼濾波的抗積分飽和PDF控制系統結構如圖4所示。

圖4　卡爾曼濾波抗積分飽和PDF算法

圖4中，w(t)為控制干擾信號(或稱過程信號)，v(t)為測量干擾信號，yv為某個時刻受到噪聲污染后的輸出信號，ye為經過卡爾曼濾波之后的輸出信號。

2.2　仿真試驗

以非接觸式登船梯做軸向旋轉補償波浪為例進行研究，用系統辨識的方法獲取研究對象的數學模型：

(11)

此數學模型實際上是直流電機的位置控制模型，通過直流電機的位置控制對波浪的波動進行補償。對其進行離散化，并將其描述成離散狀態方程，求出A、B、C、D四個矩陣的值。根據等極點原理，由式(2)、式(3)算出兩組仿真參數，仿真參數如表1所示。

(12)

(13)

(14)

w(t)控制干擾信號與v(t)測量干擾信號均為幅值為2的高斯白噪聲，兩個干擾信號的協方差值如表1所示都為1。給系統加上一個階躍信號，信號大小為50°,即讓電機轉50°，階躍響應仿真結果如圖5所示。

圖5　階躍信號仿真曲線

從仿真的結果可以看出,基于卡爾曼濾波的抗積分飽和PDF控制算法，能有效抵抗強干擾信號的影響，充分發揮了抗積分飽和PDF算法響應快、無超調的控制性能。

為了查看基于卡爾曼濾波抗積分飽和PDF算法的跟蹤性能，給系統加上正弦信號，信號的幅值為50°，角頻率為0.1，跟隨特性仿真結果如圖6所示。

圖6　跟隨信號仿真曲線

從仿真的結果可以看出，基于卡爾曼濾波抗積分飽和PDF算法的跟隨特性良好，能有效抵抗噪聲的干擾，實現信號的快速跟蹤。

3結束語

仿真表明，卡爾曼濾波抗積分飽和PDF算法在較大的隨機噪聲干擾下仍然能夠快速響應目標，抑制噪聲的干擾，保證控制器保持良好的控制品質。該控制算法實現簡單，有著廣闊的應用前景。

參考文獻

[1] 秦永元.卡爾曼濾波與組合導航原理[M].西安：西北工業大學出版社，2004.

[2] 張志利,張維勝.卡爾曼濾波在溫度監控系統中的應用[J].傳感器世界,1999,5(10):20-22.

[3] 潘志揚,潘俊民.基于Kalman濾波的無位置傳感器感應電機伺服系統的研究[J].電氣傳動,2002,32(4):13-16.

[4] 辛菁,劉丁,班建安.自適應卡爾曼濾波器在機器人控制中的應用[J].西安理工大學學報,2007,23(2):136-139.

[5] 劉立生,楊宇航.基于離散小波變換和Kalman濾波的直升機主減智能狀態預測[J].振動與沖擊,2012,31(17):159-164.

[6] Phelan R M.Automatic control system[M].New York:Cornell University Press,1977.

[7] 王學斌，徐建宏，張章.卡爾曼濾波器參數分析與應用方法研究[J].計算機應用與軟件,2012,29(6):212-215.

[8] 張鵬杰,邱衛寧,侯賀平,等.總體最小二乘求取AR(1)模型參數[J].測繪信息與工程,2012,37(3):1-2,8.

[9] 劉惟錦,章毓晉.基于Kalman濾波和邊緣直方圖的實時目標跟蹤[J].清華大學學報：自然科學版,2008,48(7):1104-1107.

[10]劉和平.數字信號處理器原理、結構及應用基礎[M].北京:機械工業出版社,2006:1-15.

中圖分類號：TP13

文獻標志碼：A

DOI:10.16086/j.cnki.issn1000-0380.201502002

修改稿收到日期：2014-06-20。

第一作者鄢華林(1957-)，男，1980年畢業于江蘇大學機械工程專業，獲學士學位，教授；主要從事電液伺服控制、海洋裝備、系留裝置的研究。