陣列校正中導向矢量內插的條件*

?

陣列校正中導向矢量內插的條件*

張興良，王可人，金虎

(電子工程學院，安徽 合肥230037)

摘要：陣列模型誤差對陣列信號處理影響嚴重，且建模困難，實際工程中通常采用內插技術進行陣列誤差校正。在對導向矢量內插法進行分析的基礎上，提出運用該方法的4個條件，即穩健性、可插性、單調性和疊加性，并給出了定義。這4個條件是誤差校正后的陣列有效工作的前提，仿真實驗驗證了該結論。提出的條件對工程實踐具有一定的指導價值。

關鍵詞：陣列信號；模型誤差；導向矢量；疊加性

0引言

陣列信號處理是信號處理領域里的一個重要分支，廣泛應用在雷達、通信、水聲和地震等諸多領域，其物理基礎是陣元輸出信號之間具有嚴格相關性，且這種相關性可以用陣列模型描述。然而，在進行陣列信號處理前，需要先對天線接收的信號進行放大和變換，不可避免地導致陣元輸出信號之間的相關性降低，影響陣列信號質量。此外，天線加工的工藝、陣元布置的精確性等許多實際因素都會影響陣列信號質量，因此實際的陣列信號與理想的陣列模型之間存在誤差，稱這種誤差為陣列模型誤差。陣列模型誤差的類型[1]主要有陣元方向圖不一致性誤差、通道幅相誤差、陣列位置誤差和陣元之間的互耦誤差等。模型誤差校正是陣列信號處理研究的一個重要課題。

傳統的誤差校正方法是導向矢量內插法[2]，該方法直接對誤差條件下的導向矢量進行離散測量、內插，工作量較大。近年來，參數化校正方法是研究熱點，參數化校正方法對模型誤差進行參數化建模，估計模型誤差的參數，校正精度高。參數化方法又可以分為有源校正[3-4]和自校正[5-6]，有源校正需要設置方位精確已知的校正源對陣列誤差進行離線估計，而自校正則不需要，自校正對陣列誤差和入射信號方向進行聯合估計，或只對入射信號方向進行估計。王布宏等[7]提出輔助陣元法(instrumental sensor method,ISM)，通過增加位置精確校正的輔助陣元對方位依賴的幅相誤差進行自校正，王鼎等[8-9]又將輔助陣元法應用到陣元位置誤差、幅相誤差、互耦誤差等具體場合。輔助陣元法依然對模型誤差進行建模處理，但在實際中，模型誤差的類型非常多，且陣列中往往同時存在多種類型的誤差，難以預測，因此對模型誤差準確建模難以實現，因此參數化校正方法效果并不明顯，導向矢量內插法依然是最實用的誤差校正方法。

不同類型的模型誤差具有不同的特性，對陣列輸出信號的影響也不一定都是線性的，因此工程中對模型誤差校正是有條件要求的。例如在理想條件下，只要陣元間隔小于入射信號半個波長，則陣列是無模糊[10]的，但當陣列中存在模型誤差時則不然。本文提出運用導向矢量內插法的4個必要條件，即穩健性、可插性、單調性和疊加性。這4個條件對MUSIC算法[11]等陣列信號處理算法至關重要，仿真實驗將證明本文的結論。

1基于內插技術的陣列誤差校正

1.1理想陣列模型

以均勻線陣為例，均勻線陣的陣列結構如圖1所示。相鄰陣元之間的間隔為d，d≤λ/2，λ為信號波長；第i個入射信號的方位角為φi，π/2≥φi≥-π/2。當有D個信號入射時，陣列輸出信號為

x(t)=As(t)+n(t),

(1)

式中：

x(t)=(x1(t),x2(t),…,xM(t))T，

(2)

n(t)=(n1(t),n2(t),…,nM(t))T，

(3)

s(t)=(s1(t),s2(t),…,sD(t))T，

(4)

(5)

(6)

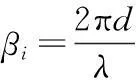
圖1　均勻線陣結構圖Fig.1　Configuration of a uniform linear array

1.2模型誤差存在條件下的導向矢量

(7)

式中：?表示點乘；F為通道誤差矢量，F=(F1，F2，…，FM)，Fm為第m個陣元的通道誤差。

(8)

1.3導向矢量內插法

首先，在觀測方向范圍內按一定步進選取離散方向點。然后，利用方向精確校準的信號源依次從各離散方向上入射陣列，由陣列輸出信號逆向求解導向矢量。最后，對導向矢量進行多維內插得到其他方向上的導向矢量。

(9)

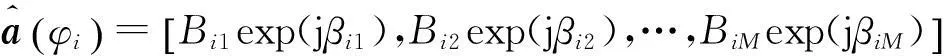
(10)

則其歸一化導向矢量為

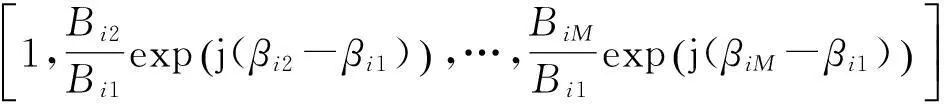
(11)

2導向矢量內插法的條件

導向矢量內插法雖然可以避免復雜的模型誤差建模，但要使該方法行之有效，需要滿足以下條件：

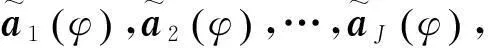
(12)

則認為陣列導向矢量是穩健的。

(2) 可插性

對離散點方向的導向矢量測量相當于對真實的導向矢量進行采樣，而非離散點方向上的導向矢量則需要通過內插獲得。內插是有信息損失的，其結果不可能與真實數據完全一致，只能盡可能逼近真實數據。如果內插的結果與真實數據較為接近，則稱導向矢量具有可插性。當導向矢量不具有可插性時，通過提高離散點方向的密度可以改善導向矢量的可插性，但會增加實際工作量。

設判斷導向矢量是否可插的門限值為Tv，φ為任意方向，若

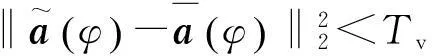
(13)

(3) 單調性

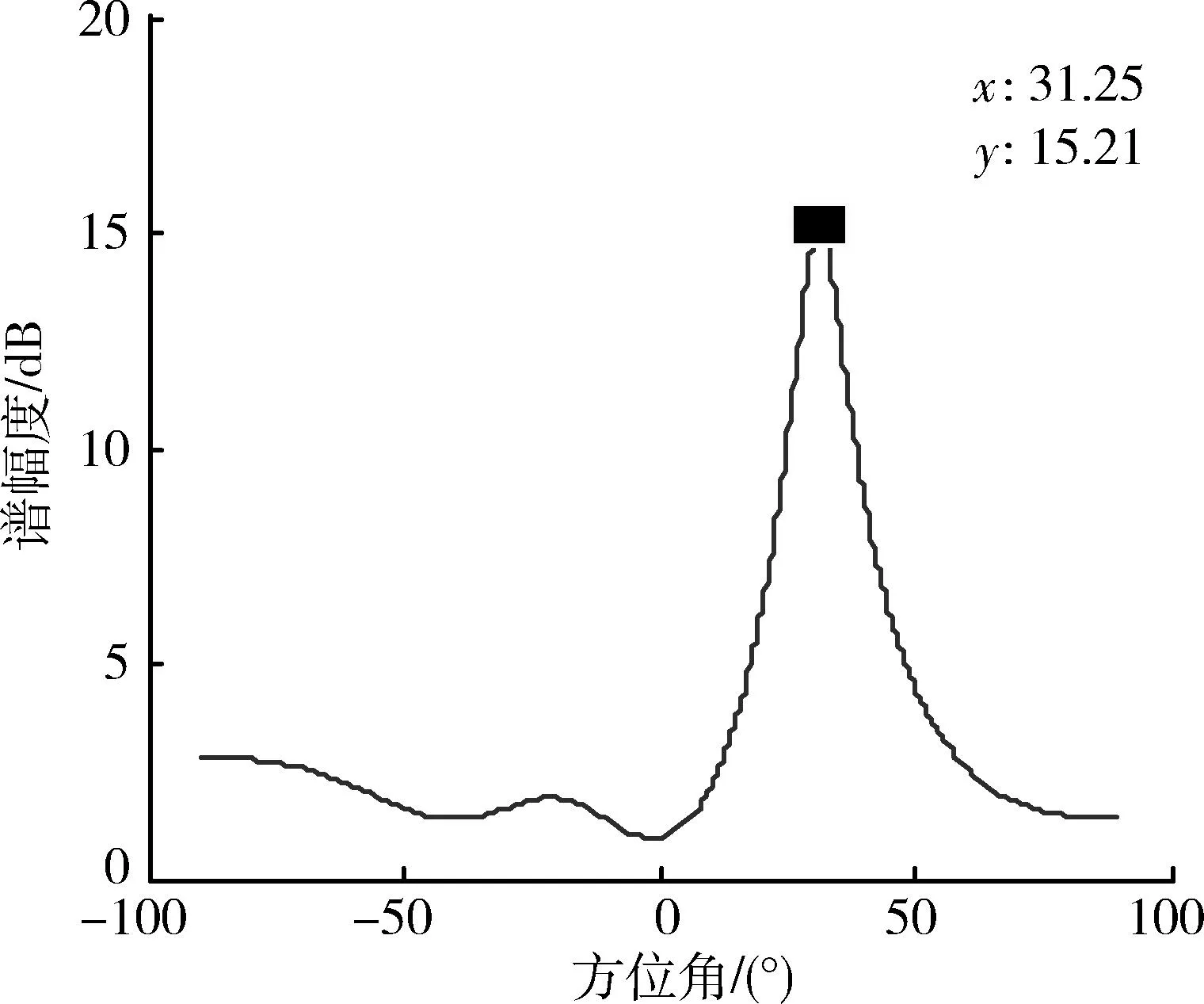
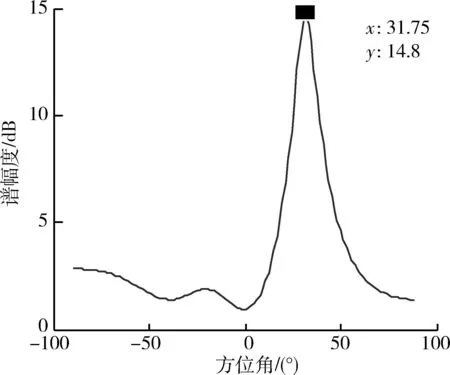
導向矢量表征的是信號入射方向與陣列之間的關系，一個導向矢量只能對應一個入射方向，否則將會產生模糊。導向矢量與信號入射方向之間一一對應的映射關系，稱為導向矢量的單調性。在理想陣列模型條件下具有單調性的導向矢量，由于模型誤差的存在，也有可能不具有單調性。設導向矢量單調性的門限為Tc，φ1和φ2為任意2個方向，若

圖2中豎坐標表示子批量，縱坐標表示選擇的工藝路線，橫坐標表示工藝路線下的所有工序；式(25)中，數組O=[ot,r]4×r分別記錄了工序加工所選擇的機床、刀具、夾具、搬運設備，r表示工序個數；式(26)中，數組W=[we,r]w×r存儲了調度過程中工序在機床上加工的順序。

(14)

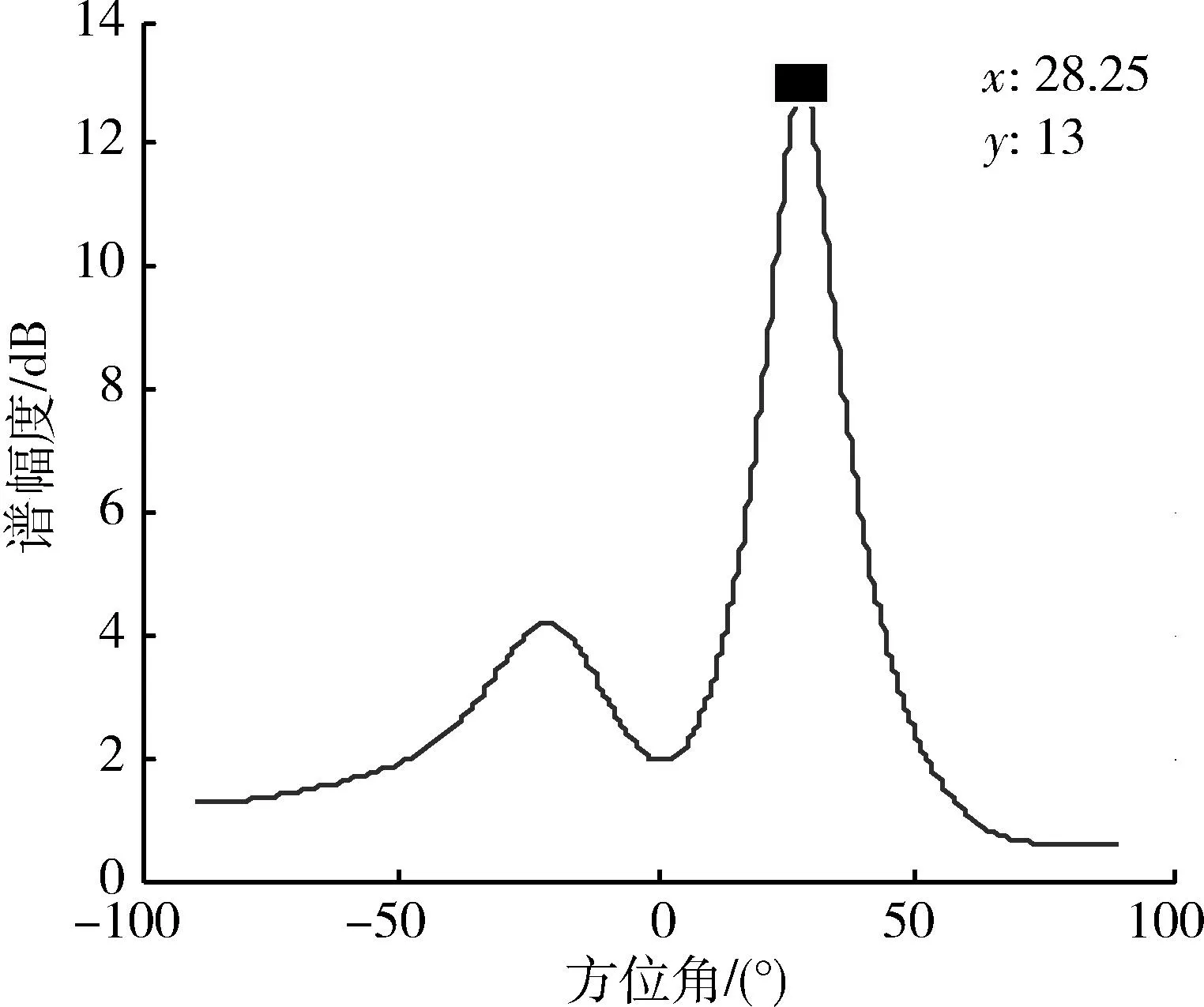
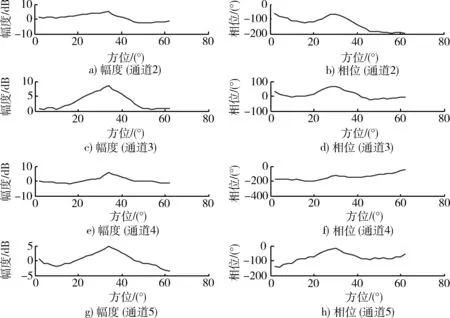
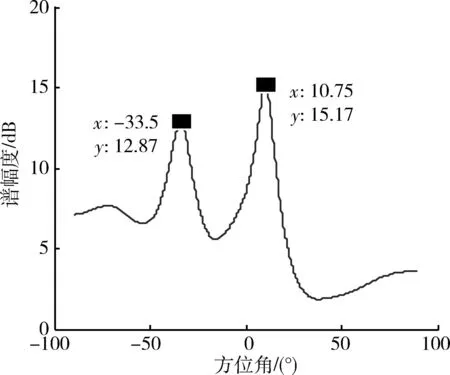
則認為導向矢量具有單調性，Tc

(4) 疊加性

陣列有可能同時接收多個不同方向的信號，每個信號對應一個導向矢量，這些導向矢量可能會相互影響，發生紊亂，這是陣列信號處理所不能接受的。當陣列同時接收多個不同方向的不相關信號，這些方向對應的導向矢量之間沒有影響，則該陣列滿足疊加性。當任意D個方向將φ1，φ2,…,φD信號入射陣列時，D

Λ(φ1,φ2,…,φD)=(a(φ1),a(φ2),…,a(φD)).

(15)

陣列輸出信號的協方差矩陣為

R=E[xxH]=ASAH+σ2I,

(16)

式中：S=E[ssH]；σ2為噪聲的方差；I為單位矩陣，σ2I=E[nnH]。對R進行特征分解，并對特征值按降序排列可得

λ1≥λ2≥…≥λD≥λD+1=…=λM，

(17)

與λ1,λ2,…,λM相對應的特征向量記為e1,e2,…,eM，前D個特征向量所張成的子空間記為ES，ES=(e1,e2,…,eD)，后面的M-D個特征向量張成的子空間記為EN，EN=(eD+1,eD+2,…,eM)。

如果該陣列滿足疊加性，根據子空間理論，ES與Λ(φ1,φ2,…,φD)等價，EN與Λ(φ1,φ2,…,φD)正交，則

(18)

由于噪聲等因素存在，αi不為0，但接近于0，即

αi

(19)

式中：tε為門限，是大于0但接近于0的常數。

式(19)即為判斷陣列是否滿足疊加性的依據，如果陣列不滿足疊加性，則不能用于接收多信號。

3仿真分析

仿真1：五元均勻線陣，陣元間距為0.3 m；利用導向矢量測量法得到離散點方向導向矢量，相鄰離散點間距為3°，通過線性插值，相鄰插值點間距為0.5°；空間有一2 GHz的信號從30°方向入射。當導向矢量的穩健性較好(擾動很小)時，通過MUSIC算法計算空間譜，見圖2。當導向矢量穩健性較差時，假設相對于測量得到的歸一化導向矢量，幅度擾動在[-0.06,0.06]的區間內均勻分布，相位擾動在[-0.05π，0.05π]的區間內均勻分布，基于MUSIC算法的空間譜圖見圖3。

圖2　空間譜圖(穩健性較好)Fig.2　Plot of spatial spectrum with great robustness

從圖中可以看出，當導向矢量穩健性較好時，MUSIC算法能夠比較準確地測出來波方向。但當穩健性較差時，不僅方向估計誤差較大，而且分辨率較低。導向矢量的穩健性是MUSIC算法的高分辨率的重要保證。

圖3　空間譜圖(穩健性較差)Fig.3　Plot of spatial spectrum with poor robustness

仿真2：五元均勻線陣，陣元間距為0.3 m，進行外場試驗，利用導向矢量測量法得到離散點方向導向矢量，再進行線性插值。當離散測量間距為2°、插值間距為0.25°時，插值后的導向矢量見圖4；當離散測量間距為6°、插值間距為0.25°時，插值后的導向矢量見圖5。空間有一2 GHz的信號從31°方向入射，在兩種插值情形下的空間譜圖分別為圖6和圖7。

圖4　導向矢量圖(離散測量間距為2°、插值間距為0.25°)Fig.4　Plot of steering vectors when the measuring step is 2° and the interpolated step is 0.25°

圖5　導向矢量圖(離散測量間距為6°、插值間距為0.25°)Fig.5　Plot of steering vectors when the measuring step is 6° and the interpolated step is 0.25°

圖6　空間譜圖(滿足可插性)Fig.6　Plot of spatial spectrum with great insertability

圖7　空間譜圖(不滿足可插性)Fig.7　Plot of spatial spectrum with poor insertability

圖4和圖5截取了一部分陣列流型的幅度圖和相位圖，其中通道1(陣元1)是參考通道，故未顯示。在誤差存在條件下，從陣列流型幅度圖和相位圖中很難發現規律性，說明誤差對陣列流型的影響時比較明顯的。當離散測量間距為2°時，陣列流型的細節變化比較清楚；當離散測量間距為6°時，陣列流型信息損失嚴重。圖6中的來波方向估計誤差較小，而在圖7中誤差較為嚴重，說明空間譜估計對陣列流型誤差較為敏感，式(13)可以檢驗陣列流型的可插性。

仿真3：五元均勻線陣，陣元間距為0.3 m；測量得到離散點方向導向矢量并進行插值，相鄰插值點間距為0.5°。由于模型誤差的影響，30°方向和-22°方向的導向矢量非常接近。空間一信號從-22°方向入射陣列，空間譜圖見圖8。

MUSIC算法通過辨別導向矢量獲得入射信號的方向，當導向矢量不具有單調性時，MUSIC算法無法有效辨別入射信號方向。因此，雖然空間只有一個信號從-22°方向入射，但是在圖8中可以看出30°方向的峰值也非常明顯，嚴重影響著基于MUSIC算法的來波方向估計結果。MUSIC算法的有效性非常依賴導向矢量的單調性。

仿真4：五元均勻線陣，陣元間距為0.3 m；測量得到離散點方向導向矢量并進行插值，相鄰插值點間距為0.5°；兩信號入射，入射方向分別為-30°和20°。當陣列滿足疊加性時，其空間譜估計結果如圖9。當2個入射方向的導向矢量受到影響時，不妨將其受到的影響等效為擾動，并假設擾動與方向無關，僅與方向差有關。設幅度擾動在[-0.06Δθ,0.06Δθ]的區間內均勻分布，相位擾動在[-0.05πΔθ，0.05πΔθ]的區間內均勻分布，其中Δθ為方向差。此時空間譜估計結果如圖10所示。

圖8　空間譜(不滿足單調性)Fig.8　Plot of spatial spectrum with poor monotonicity

圖9　空間譜圖(滿足疊加性)Fig.9　Plot of spatial spectrum with great superposition

圖10　空間譜圖(不滿足疊加性)Fig.10　Plot of spatial spectrum with poor superposition

MUSIC算法通過辨別導向矢量估計來波方向，當導向矢量發生紊亂時，MUSIC算法失效不可避免。圖9中可以識別來波方向，但在圖10中，由于導向矢量不滿足疊加性，來波方向不明顯，且估計不準確。陣列導向矢量的疊加性是MUSIC算法的前提。

4結束語

對陣列模型誤差進行參數化建模的誤差校正方法在實際工程中并不實用，導向矢量測量法是一種較為有效的模型誤差校正方法，但運用該方法是有條件要求的。本文給出了4個條件，即穩健性、可插性、單調性和疊加性，仿真實驗證明了這4個條件是導向矢量測量法行之有效的必要條件。實際上，參數化建模的校正方法也是有條件要求的，有待后續研究提出。

參考文獻：

[1]柳艾飛. 陣列測向與陣列校正技術研究[D]. 西安: 西安電子科技大學, 2012: 21-25.

LIU Ai-fei. Research on Direction Finding and Array Calibration Techniques[D]. Xi′an: Xidian University, 2012: 21-25.

[2]SCHMIDT R O. Multilinear Array Manifold Interpolation[J]. IEEE Transactions on Signal Processing, 1992, 40(4): 857-866.

[3]PARK H Y, LEE C Y, KANG H G, et al. Generalization of Subspace-Based Array Shape Estimations[J]. IEEE Journal of Oceanic Engineering, 2004, 29(3): 847-856.

[4]WANG D,WU Y. Array Errors Active Calibration Algorithm and Its Improvement[J]. Science China Information Sciences, 2010, 53(5): 1016-1033.

[5]FRIEDLANDER B, WEISS A J. Direction Finding in the Presence of Mutual Coupling[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(3): 273-284.

[6]WIJNHOLDS S J, VEEN A J. Multisource Self-Calibration for Sensor Arrays[J]. IEEE Transactions on Signal Processing, 2009, 57(9): 3512-3522.

[7]王布宏, 王永良, 陳輝, 等. 方位依賴陣元幅相誤差的輔助陣元[J]. 中國科學: 信息科學, 2004, 34(8): 906-918.

WANG Bu-hong, WANG Yong-liang, CHEN Hui, et al. Array Calibration of Angularly Dependent Gain and Phase Uncertainties with Carry-on Instrumental Sensors[J]. Science in China Series E: Information Sciences, 2004, 34(8): 906-918.

[8]王鼎, 吳瑛. 陣元位置誤差自校正的累積量域輔助陣元法[J]. 系統工程與電子技術, 2010, 32(7):1357-1364.

WANG Ding, WU Ying. Cumulants-Based Instrumental Sensors Method for Self-Calibration of Sensor Position Errors[J]. Systems Engineering and Electronics, 2010, 32(7):1357-1364.

[9]王鼎, 吳瑛. 基于輔助陣元的陣列誤差有源校正算法[J]. 中國科學: 信息科學, 2011,41(5): 626-637.

WANG Ding, WU Ying. Array Errors Active Calibration Algorithm Based on Instrumental Sensors[J]. Science in China Series E: Information Sciences, 2011,41(5): 626-637.

[10]何子遠. 稀疏陣DOA估計及模糊特性研究[D]. 成都: 電子科技大學, 2009: 57-78.

HE Zi-yuan. Research on DOA Estimation and the Ambiguities for Sparse Arrays[D]. Chengdu: University of Electronic Science and Technology of China, 2009:57-78.

[11]張小飛,汪飛,徐大專. 陣列信號處理的理論和應用[M]. 北京:國防工業出版社,2010.

ZHANG Xiao-fei, WANG Fei, XU Da-zhuan. The Theory and Application of Array Signal Processing[M]. Beijing: National Defense Industry Press,2010.

[12]CHAPRA S C, CANALE R P. Engineering Numerical Methods [M]. New Delhi: Tata McGraw-Hill, 2002.

Requirement of Steering Vector Interpolation in Array Calibration

ZHANG Xing-liang，WANG Ke-ren，JIN Hu

(Electronic Engineering Institute,Anhui Hefei 230037, China)

Abstract:Array signal processing is adversely affected by array model errors. Considering that model errors are difficult to be modeled, the interpolation technology is usually used to calibrate them in practice. Based on the analysis on the method of steering vector interpolation, four defined requirements, i.e.robustness, insertability, monotonicity and superposition are proposed to apply this method. Those requirements are prerequisites for array working. This conclusion is demonstrated by the results of simulation experiments. Therefore, the proposed requirements are valuable in engineering practice.

Key words:array signal; model error; steering vector; superposition

中圖分類號：TN911.23

文獻標志碼：A

文章編號：1009-086X(2015)-02-0076-06

doi:10.3969/j.issn.1009-086x.2015.02.013

通信地址：230037安徽省合肥市黃山路460號402室E-mail：305755450@qq.com

作者簡介：張興良(1985-)，男，安徽廬江人。博士生，研究方向為陣列信號處理。

* 收稿日期：2014-04-23；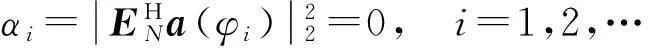
修回日期：2014-05-21