采用非線性Galerkin方法的柔性梁模型降階研究
滿興博,伍曉紅,孫清
(1.西安交通大學土木工程系, 710049, 西安;2.西安交通大學航天航空學院, 710049, 西安)
?
采用非線性Galerkin方法的柔性梁模型降階研究
滿興博1,伍曉紅2,孫清1
(1.西安交通大學土木工程系, 710049, 西安;2.西安交通大學航天航空學院, 710049, 西安)
針對采用Galerkin方法獲取的結構動力學降階模型精度不高的問題,以考慮幾何非線性的兩端固支柔性梁作為研究對象,建立了兩端固支柔性梁非線性動力學模型。首先采用Galerkin方法將原系統降階,得到單自由度、三自由度和五自由度系統,再采用非線性Galerkin方法將二自由度和三自由度系統降階為單自由度系統。通過分析降階模型的非線性動力學行為,得到系統響應隨外荷載幅值變化的分岔圖,給出系統做周期運動、倍周期運動和混沌時的時程曲線、相圖與龐加萊映射圖。在特定頻率下,通過改變外荷載幅值來控制系統進出混沌狀態。與Galerkin方法得到的降階模型進行了對比,通過比較進出混沌狀態時的外荷載幅值,分析了兩種方法的降階效果。結果表明:非線性Galerkin方法能夠有效提高降階模型的精度,更接近真實模型;采用非線性Galerkin方法降階得到相同自由度的低階系統時,原模型階數越高,得到的低階模型越精確。
柔性梁;模型降階;非線性Galerkin方法;非線性動力學行為;分岔
近年來,機械工程領域中機器人及各種操作手向著高速、精密、輕量化的方向發展,非線性機械臂的振動控制日益受到重視[1-4];在航天領域,由于太空中幾乎不存在空氣阻力,由超薄超輕材料制造的天線和太陽能電池板等結構一旦開始振動,將持續很長時間,航天器結構的振動控制問題急需解決[5-7];在土木工程中,工程結構的尺度越來越大,例如超高層建筑、大跨度橋梁等,結構自身表現出明顯的幾何非線性,由風載及地震引起的結構振動問題日益突出[8-10]。
由于實際的結構是一個無限維、模態密集的空間分布系統,如果想要控制結構的振動,須采用有效的降階方法來獲取階數較低、有足夠精度的模型,在此基礎上進行控制方法的設計。因此,對實際結構進行模型降階就成為一個關鍵問題,這一問題為建立結構仿真模型和進行結構振動控制帶來了困難。
研究非線性動力系統時常采用的模型降階方法有中心流形方法[11-12]、Lyapunov-Schmidt(L-S)方法[11-13]、非線性Galerkin方法[14-15]和本征正交分解技術(POD)[16]等,其中中心流形方法和L-S方法通常僅適用于局部平衡點附近問題的降階,在實際應用中有局限性。POD技術是一種線性處理方法,有如下問題:①過高估計系統的階數;②不能提供變量之間的非線性關系;③依賴于已有數據,對于同一系統的不同狀態信號可能構造出不同的系統。
非線性Galerkin方法是在Galerkin方法的基礎上發展起來的。在Galerkin方法中,高維或無窮維動力系統被投影到由假設模態所構成的子空間中,這些假設模態通常是線性算子的特征值對應的特征向量,在傳統的Galerkin方法中通常是根據經驗直接截斷獲得,不考慮高階分量的影響。但是,這種直接截斷的方法有不足之處,忽略了高階分量對結構的影響,對非線性系統可能得出錯誤的結論。為了改進Galerkin方法,根據近似慣性流形的構造思想,Marion和Temam提出了非線性Galerkin方法,該方法的核心之處在于:采用低階分量描述原系統的同時考慮了高階分量的影響,從而有較高的精度和收斂速度。
本文以考慮幾何非線性的兩端固支柔性梁作為研究對象,建立了兩端固支柔性梁非線性動力學模型,并采用非線性Galerkin方法對所建立的模型進行降階。與Galerkin方法得到的低階模型結果進行了對比,通過比較進入混沌時的外荷載幅值,分析兩種方法的降階效果。結果表明,基于非線性Galerkin方法得到的低階模型比Galerkin方法得到的低階模型更接近真實結構。
1 柔性梁模型的建立
本文研究對象為伯努利-歐拉梁,建模時考慮變形過程中軸向應變引起的軸向力對系統剛度的影響,即考慮了系統的幾何非線性。柔性梁模型如圖1所示。
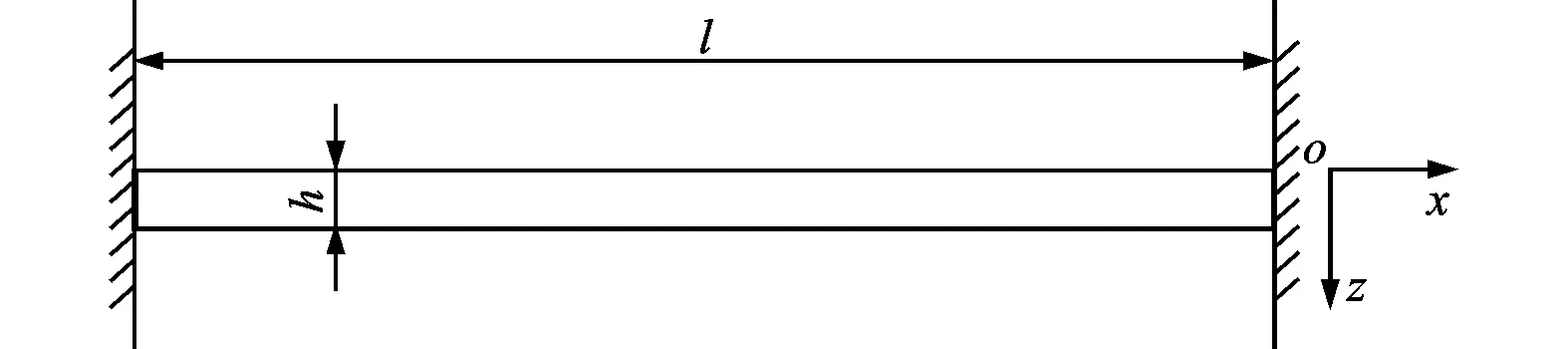
圖1 兩端固支柔性梁示意圖
當梁沿軸線受一均布力f(x,t)時,沿軸線截取一微元dx,受力分析如圖2所示。

圖2 微元受力分析圖
根據達朗貝爾原理,可得微元在z方向的動力學平衡方程
(1)
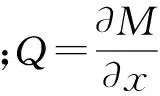
式(1)可簡化為
(2)
對于兩端固支梁,邊界條件為
(3)
2 基于非線性Galerkin方法的模型降階
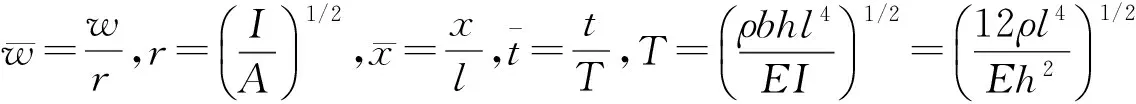
(4)
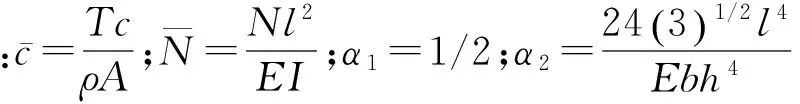
令
(5)
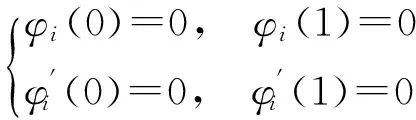
將式(4)兩端乘以φn(x),再將式(5)代入式(4),方程兩端從x=0到x=1積分,可得
(6)
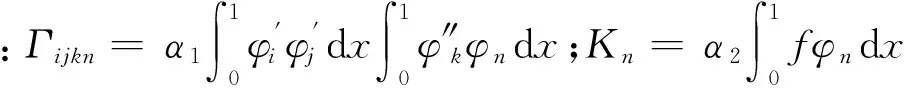
傳統Galerkin方法通常對式(6)直接進行模態截斷,不考慮高階分量的影響,從而得低階模型。例如,想得到單自由度系統,直接令m=1,n=1得
(7)
非線性Galerkin方法得到的單自由度系統不但包含低階分量,同時也需考慮高階分量的影響。考慮梁的中點有一正弦激勵的情形,一般認為這種情況下響應中不會有反對稱模態存在。如取高階分量為2階模態,即m=3,當n分別取1、3時得到二自由度微分方程組,再考慮模態的對稱性,有
(8)
(9)
下面采用非線性Galerkin方法得到反映u3與u1關系的近似慣性流形。
構造近似慣性流形常用的方法有不動點法和隱式歐拉解法,由于不動點法方便數值求解,因此本文采用不動點法求解近似慣性流形。
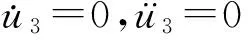
(10)
由于u3為小量,忽略二階及以上無窮小,得到反映u3與u1關系的近似慣性流形,即
(11)
再將u3代入式(8),得到降階系統
(12)
故得到式(2)的近似解為
(13)
3 柔性梁非線性動力學行為分析
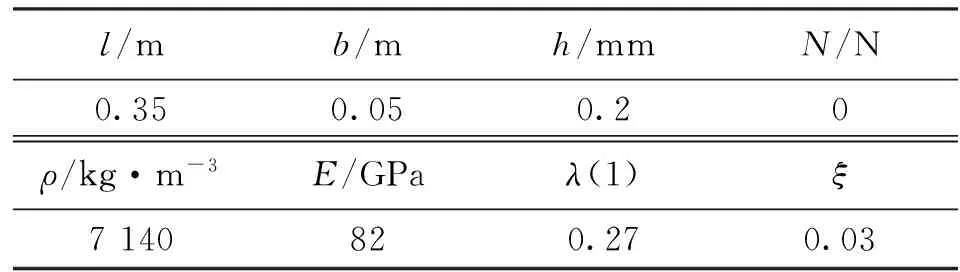
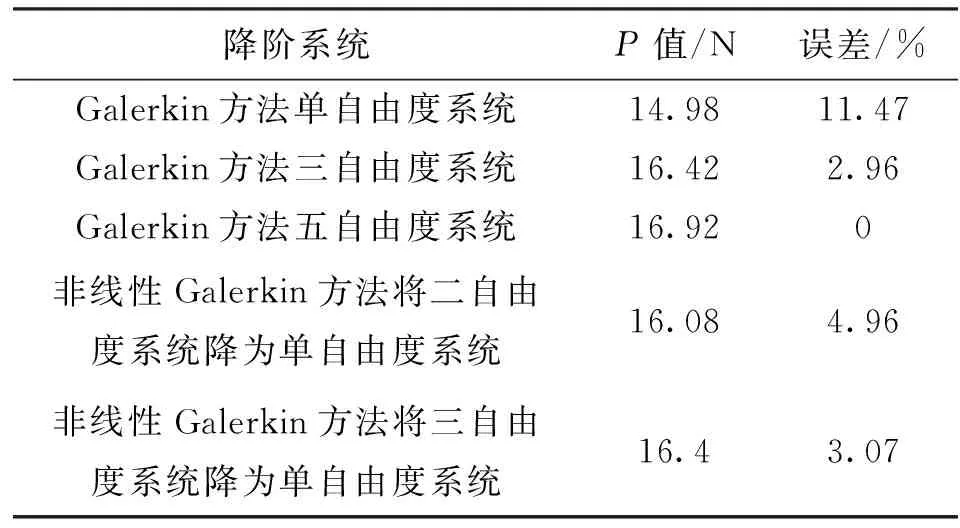
表1 柔性梁參數
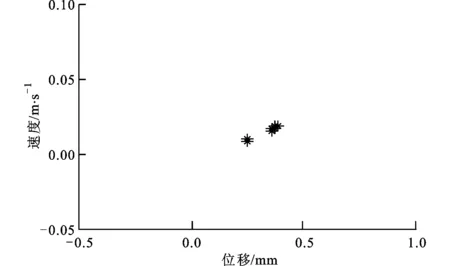
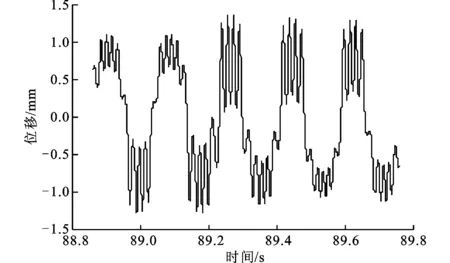
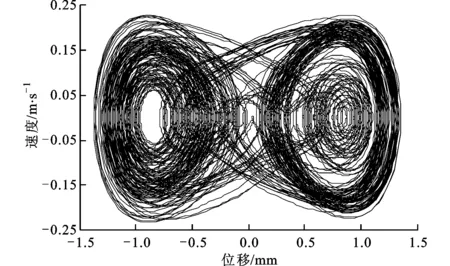
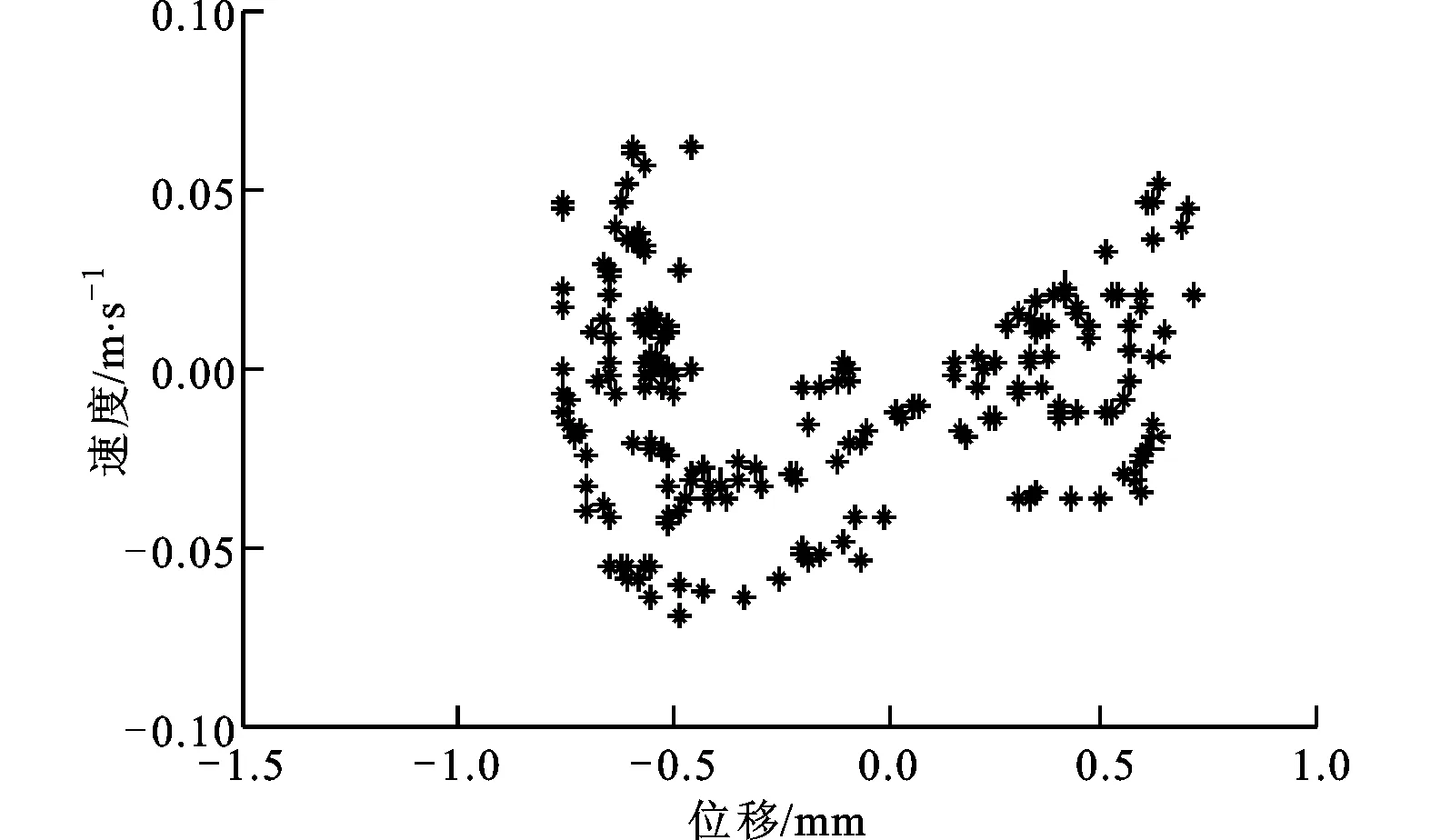
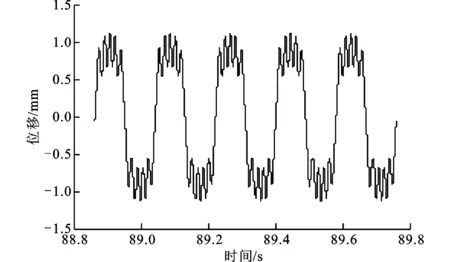
梁在中點處受到正弦激勵,f(t)=Psinωt,外荷載幅值為P,外荷載頻率ω=35 rad/s。計算不同外荷載幅值P下柔性梁l/4處的響應,可得到l/4處位移隨P變化的分岔圖,如圖3a所示,P取值0≤P≤20 N。為了清楚顯示,圖3b為P取值4 N≤P≤6 N的分岔圖。

(a)0≤P≤20 N
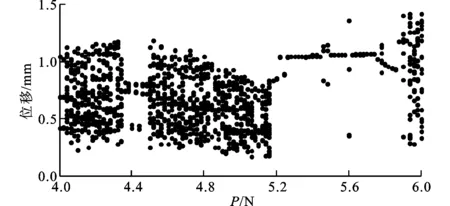
(b)4 N≤P≤6 N圖3 P為變量的分岔圖
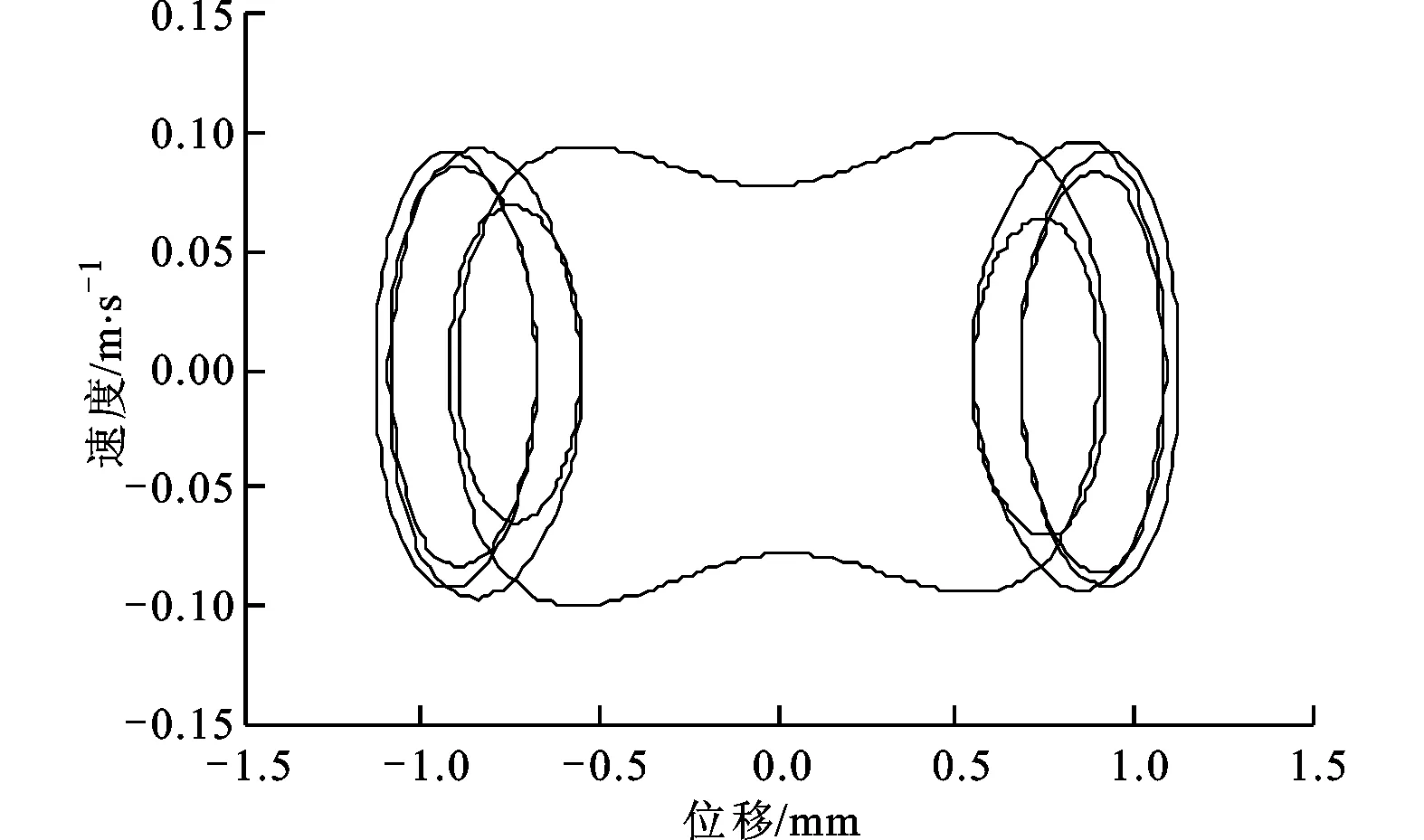
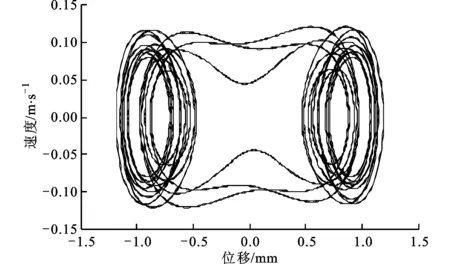
從圖3b可以看出,在4 N≤P≤4.32 N時系統進行混沌運動;當4.32 N (a)時程響應曲線 (b)相平面圖 (c)龐加萊截面圖4 2倍周期運動(P=4.46 N) (a)時程響應曲線 (b)相平面圖 (c)龐加萊截面圖圖5 混沌運動(P=5 N) (a)時程響應曲線 (b)相平面圖 (c)龐加萊截面圖圖6 周期運動(P=5.3 N) (a)時程響應曲線 (b)相平面圖 (c)龐加萊截面圖7 3倍周期運動(P=5.46 N) 當P=4.46 N時,系統響應如圖4所示。由圖4c可以看出,龐加萊截面中有2個映射點,系統做2倍周期運動。當P=5 N時,系統響應如圖5所示。由圖5c可以看出,龐加萊截面上出現了一些不規則的點,而這些點又滿足一定的分布規律,系統做混沌運動。當P=5.3 N時,系統響應如圖6所示。由圖6c可以看出,龐加萊截面中只有1個映射點,系統做周期運動。當P=5.46 N時,系統響應如圖7所示。由圖7c可以看出,龐加萊截面中有3個映射點,系統做3倍周期運動。 首先,采用Galerkin方法將原系統降階,得到單自由度系統、三自由度系統、五自由度系統。在此基礎上,采用非線性Galerkin方法將二自由度系統和三自由度系統降階為單自由度系統。然后,分析各系統的非線性動力學行為,與Galerkin方法得到的低階模型進行對比,比較兩種方法的降階效果。 分別計算不同系統隨幅值P變化的分岔圖,結果如圖8所示,圖中垂線為系統進入混沌運動時的外荷載幅值。 如表2所示,比較各系統進入混沌運動時的外荷載幅值,并視Galerkin方法五自由度系統為精確解,可得各系統的降階效果。 表2 各系統進入混沌時的外荷載幅值及誤差 由表2可以看出,對于同為一階的降階系統,采用非線性Galerkin方法得到的單自由度系統比采用Galerkin方法得到的單自由度系統擁有更高的精度,更接近真實模型。 另外,同樣采用非線性Galerkin方法降階,由三自由度系統降階得到的單自由度系統比由二自由度系統降階得到的單自由度系統擁有更高的精度。 (a)Galerkin方法單自由度系統 (b)Galerkin方法三自由度系統 (c)Galerkin方法五自由度系統 (d)二自由度降為單自由度系統 (e)三自由度降為單自由度系統圖8 各系統隨外荷載幅值P變化的分岔圖 本文采用非線性Galerkin方法對所建立的兩端固支柔性梁模型進行降階,并分析了降階模型的非線性動力學行為,得到系統響應隨外荷載幅值變化的分岔圖。與Galerkin方法得到的低階模型進行對比,通過比較進出混沌狀態時的外荷載幅值,分析了兩種方法的降階效果,得到如下結論。 (1)在特定頻率下,隨著外荷載幅值的變化,系統分別進行周期運動、擬周期運動、混沌運動,因此可以通過改變外荷載幅值來控制系統進、出混沌狀態。 (2)采用非線性Galerkin方法得到的降階模型考慮了高階分量的影響,比采用Galerkin方法得到的降階模型擁有更高的精度,更接近真實模型。 (3)采用非線性Galerkin方法降階得到相同自由度的低階系統時,原模型階數越高,得到的低階模型越精確。 [1] CASTRI C D, MESSINA A. Exact modeling for control of flexible manipulators [J]. Journal of Vibration and Control, 2012, 18(10): 1526-1551. [2] QIU Z, WANG B, ZHANG X, et al. Direct adaptive fuzzy control of a translating piezoelectric flexible manipulator driven by a pneumatic rodless cylinder [J]. Mechanical Systems and Signal Processing, 2013, 36(2): 290-316. [3] KHAIRUDIN M, MOHAMED Z, HUSAIN A R. Dynamic model and robust control of flexible link robot manipulator [J]. Telkomnika Telecommunication, Computing, Electronics and Control, 2013, 9(2): 279-286. [4] ABDULLAHI A M, MOHAMED Z, MUHAMMAD M. A PD-type fuzzy logic control approach for vibration control of a single-link flexible manipulator [J]. International Journal of Research in Engineering and Science, 2013, 1(4): 37-47. [5] FENG Z, ZHANG Q, TANG Q, et al. Control-structure integrated multiobjective design for flexible spacecraft using MOEA/D [J]. Structural and Multidisciplinary Optimization, 2014, 50(2): 347-362. [6] SALES T P, RADE D A, DE SOUZA L C G. Passive vibration control of flexible spacecraft using shunted piezoelectric transducers [J]. Aerospace Science and Technology, 2013, 29(1): 403-412. [7] XU W, MENG D, CHEN Y, et al. Dynamics modeling and analysis of a flexible-base space robot for capturing large flexible spacecraft [J]. Multibody System Dynamics, 2014, 32(3): 357-401. [8] ZEMP R, de LLERA LA J C, ALMAZN J L. Tall building vibration control using a TM-MR damper assembly [J]. Earthquake Engineering & Structural Dynamics, 2011, 40(3): 339-354. [9] XING C, WANG H, LI A, et al. Study on wind-induced vibration control of a long-span cable-stayed bridge using TMD-type counterweight [J]. Journal of Bridge Engineering, 2013, 19(1): 141-148. [10]MASHNAD M, JONES N P. A model for vortex-induced vibration analysis of long-span bridges [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014(134): 96-108. [11]CHEN Y, LEUNG A Y T. Bifurcation and chaos in engineering [M]. Berlin, Germany: Springer, 1998. [12]陳予恕. 非線性動力學系統的分岔和混沌理論 [M]. 北京: 高等教育出版社, 1993. [13]陳啟韶. 分岔與奇異性 [M]. 上海: 上海科技教育出版社, 1995. [14]MARION M, TEMAM R. Nonlinear Galerkin methods [J]. SIAM Journal on Numerical Analysis, 1989, 26(5): 1139-1157. [15]DAI H H, PAIK J K, ATLURI S N. The global nonlinear Galerkin method for the analysis of elastic large deflections of plates under combined loads: a scalar homotopy method for the direct solution of nonlinear algebraic equations [J]. Computers Materials and Continua, 2011, 23(1): 69-99. [16]XIE D, XU M, DOWELL E H. Proper orthogonal decomposition reduced-order model for nonlinear aeroelastic oscillations [J]. AIAA Journal, 2014, 52(2): 229-241. (編輯 趙煒) Study on the Model Order Reduction of Flexible Beam Based on Nonlinear Galerkin Method MAN Xingbo1,WU Xiaohong2,SUN Qing1 (1. Department of Civil Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, China) A nonlinear dynamics model of a flexible beam clamped at both ends is established, and the order of the model is reduced using nonlinear Galerkin method to solve the problem of low accuracy using common Galerkin method. On this basis, the nonlinear dynamical behaviors of the reduced-order model are analyzed, and the bifurcation diagram of system response is obtained when the external load amplitude changes. The time-displacement curves, phase diagrams and Poincare maps are drawn when the system is put in periodic motion, quasi-periodic motion and chaotic motion. Experimental results show that the reduced-order model using nonlinear Galerkin method has higher accuracy than common Galerkin method, especially when the original model has a relatively high order. flexible beam; order reduction; nonlinear Galerkin method; nonlinear dynamic behavior; bifurcation 2014-12-29。 滿興博(1992—),男,碩士生;孫清(通信作者),男,教授,博士生導師。 國家自然科學基金資助項目(11172226)。 時間:2015-04-22 10.7652/xjtuxb201507019 TH117.5 A 0253-987X(2015)07-0113-07 網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150422.1444.002.html

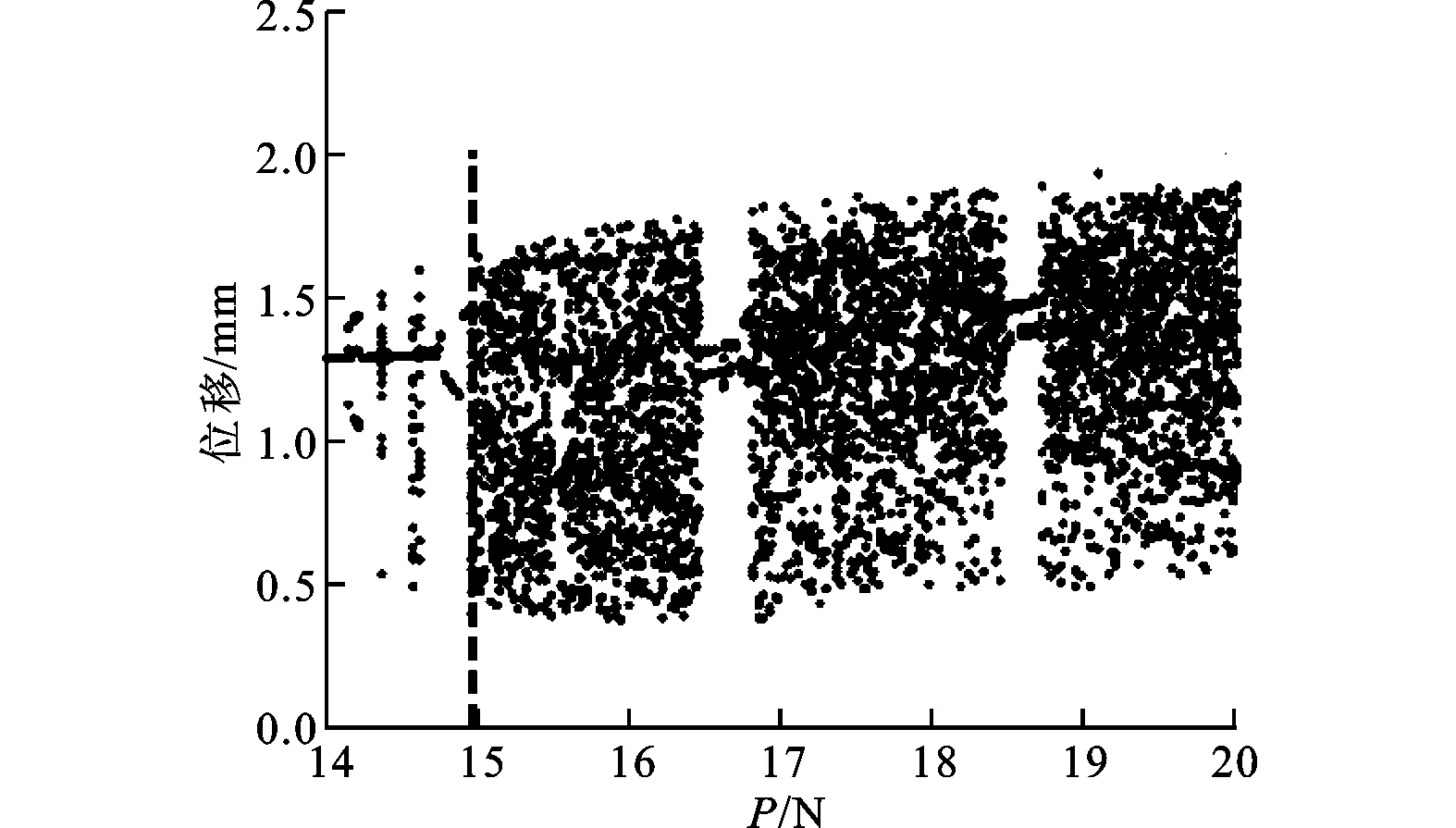
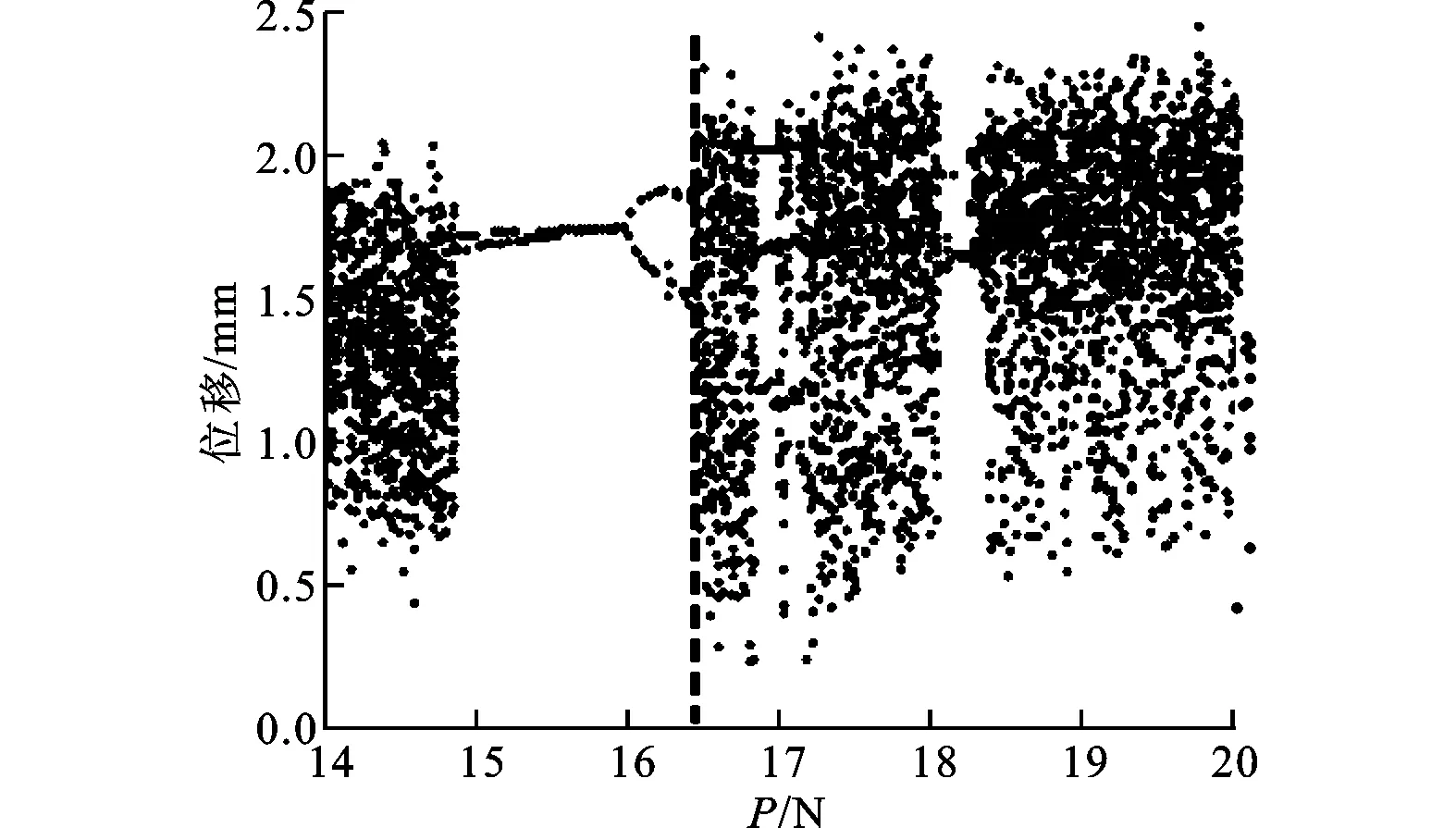
4 降階系統非線性動力學行為對比分析
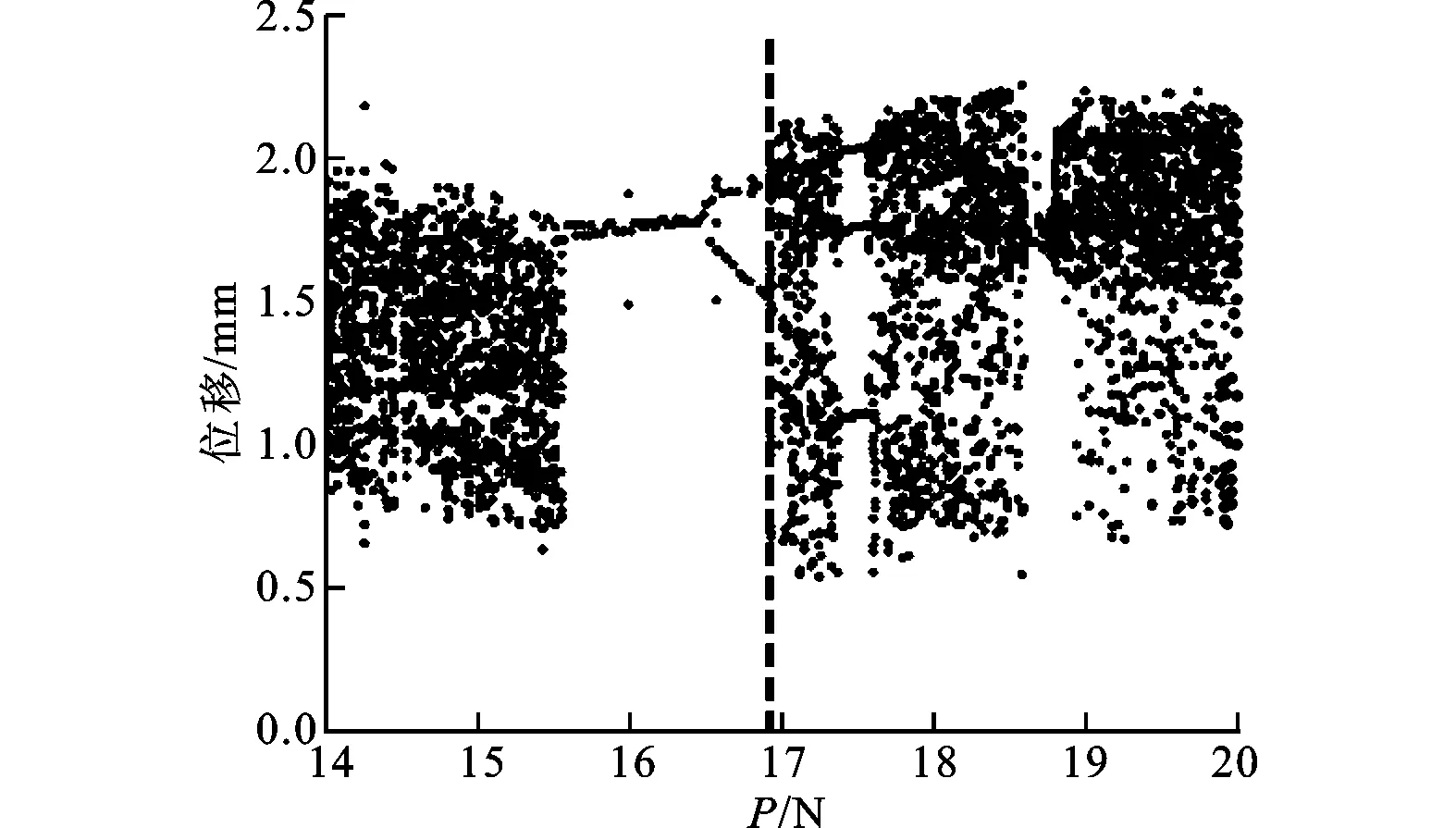

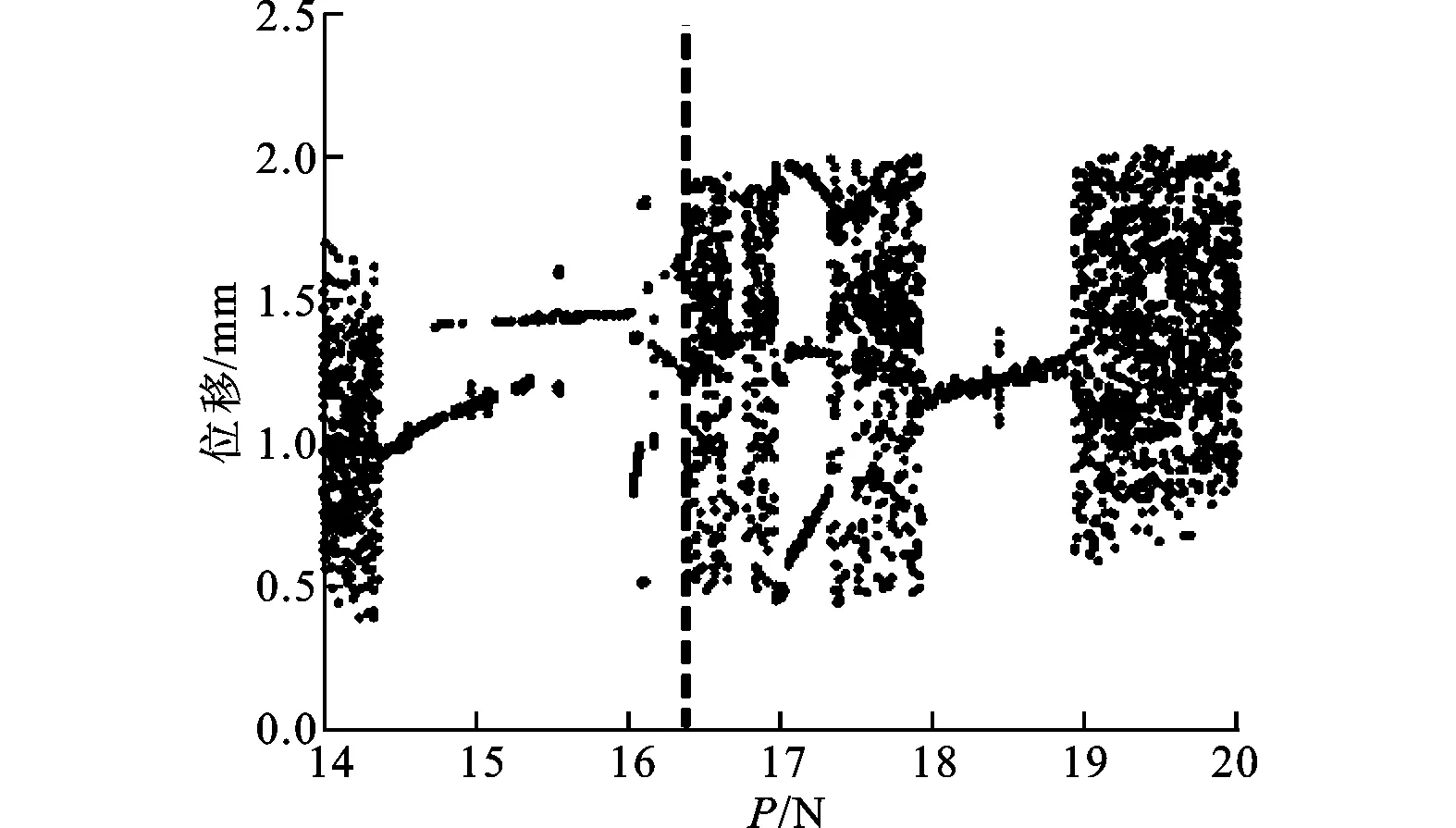
5 結 論

