混合潤滑狀態下濾波減速器的嚙合沖擊分析與修形方法

褚坤明,王家序,,3,蒲偉,周廣武,張瑩

(1.四川大學制造科學與工程學院, 610065, 成都;2.四川大學空天科學與工程學院, 610065, 成都;3.重慶大學機電傳動與運載裝備研究所, 400044, 重慶)

?

混合潤滑狀態下濾波減速器的嚙合沖擊分析與修形方法

褚坤明1,王家序1,2,3,蒲偉2,周廣武2,張瑩1

(1.四川大學制造科學與工程學院, 610065, 成都;2.四川大學空天科學與工程學院, 610065, 成都;3.重慶大學機電傳動與運載裝備研究所, 400044, 重慶)

針對濾波減速器的嚙合沖擊問題,綜合考慮轉速、負載和真實齒面粗糙度等因素的影響,建立了反映減速器實際工況的混合潤滑數學模型,給出了混合潤滑狀態下摩擦因數的計算方法,并對不同轉速下齒輪嚙入點的潤滑狀態進行了數值計算。在此基礎上,提出了針對減速器實際工況的齒廓修形方法,建立了減速器有限元模型,并分析了齒面摩擦、齒廓修形及潤滑狀態對減速器嚙合沖擊的影響。結果表明:在混合潤滑狀態下,齒面摩擦因數隨轉速增大而減小;相比無摩擦接觸,齒面有摩擦接觸可明顯降低齒輪的嚙合沖擊,改善齒輪的接觸狀態,因此在濾波減速器的嚙合沖擊研究中,齒面摩擦因素不可或缺。有限元分析結果顯示:輸出齒輪修形量為46 μm、雙聯齒輪修形量為30 μm是改善減速器動力學性能的最佳修形量,而過小或過大的修形量都不能有效降低齒輪的嚙合沖擊;齒面潤滑狀態對減速器修形后的嚙合沖擊有較大影響,與轉速相比,齒面摩擦的影響不明顯,較高的轉速可導致濾波減速器產生較大的嚙合沖擊。

濾波減速器;混合潤滑;齒廓修形;有限元;嚙合沖擊

濾波減速器是王家序教授等發明的一種新型漸開線少齒差精密減速器[1]。作為大傳動比、高效率的減速器,其傳動效率、可靠性及傳動精度在很大程度上由齒面潤滑狀態及齒輪嚙合傳動的動力學特性決定,因此深入研究濾波減速器齒面潤滑及動力學特性,探討修形方法對濾波減速器動力學性能的影響,對提高減速器的綜合性能具有理論指導意義和工程實用價值。

Ren等運用快速傅里葉變換方法對粗糙表面的三維線接觸潤滑進行了分析,在模型中將y方向視為有限長,并考慮了真實表面粗糙度的影響[2]。蒲偉等綜合考慮了濾波減速器的齒間載荷分配、齒面粗糙度等因素,在y方向有限長假設的基礎上,利用牛頓(有限元)法得到了齒間油膜厚度、壓力的分布規律[3]。張有忱研究了齒輪齒面摩擦因數的變化規律,指出齒面綜合曲率半徑變化率對齒面摩擦因數有一定的影響[4]。周澤波研究了彈流潤滑狀態下齒輪的嚙合效率,經過試驗驗證指出,齒輪的潤滑狀態對嚙合效率有顯著影響[5]。馮海生等通過動力學模型分析了齒面摩擦對齒輪傳動效率及動力學性能的影響,指出齒面接觸應力在油膜存在的情況下減小,且隨著齒面摩擦因數的增大而增大[6]。盧立新等在齒輪傳動彈流潤滑分析的基礎上指出,膜厚及壓力的變化導致沖擊,在齒輪嚙入點處膜厚大幅度減小,因此在實際工程問題中應考慮嚙入點處的膜厚及摩擦因數[7-8]。周長江等建立了直齒輪線外嚙入沖擊摩擦模型,反推了各接觸點的沖擊摩擦力與摩擦因數[9]。劉文吉等在用有限元軟件建立了濾波減速器多齒嚙合模型的基礎上,分析了齒廓修形對輪齒嚙入嚙出沖擊及齒頂刮行的影響,但并未考慮不同的修形量及齒面摩擦因素[10]。李諍對直齒輪齒根動應力進行了分析,指出齒面摩擦因素對接觸應力有顯著影響[11]。

本文旨在綜合考慮輪齒的有限長、真實表面粗糙度等因素,在論文[3]中建立的能反映濾波減速器實際工況的混合潤滑模型的基礎上,深入探討混合潤滑狀態下濾波減速器齒面摩擦因數的計算方法,并分析轉速對輪齒嚙入點摩擦因數的影響。在此基礎上,研究對比濾波減速器在齒面無摩擦與有摩擦情況下的輪齒嚙合沖擊情況,并在混合潤滑狀態下,分析齒廓修形參數對減速器嚙合沖擊的影響,以期為濾波減速器的進一步優化設計提供理論依據。

1 濾波減速器混合潤滑建模與分析

1.1 幾何模型

濾波減速器采用N-N型漸開線少齒差行星齒輪傳動,輪齒嚙合示意圖見圖1。圖中表示的是雙聯外齒輪Z1和輸出內齒輪Z2的嚙合齒輪對,輪齒在B2點(齒輪Z2的齒頂圓與嚙合線的交點)開始進入嚙合,從B1點(齒輪Z1的齒頂圓與嚙合線的交點)脫離嚙合,K1、K2點為單、雙齒嚙合界點。

1.2 載荷分配模型

濾波減速器屬于少齒差行星傳動,其載荷分配模型采用下式[12-13]

(1)

式中:θi為外齒輪附加轉角;δi為輪齒嚙合點處的法向變形;Wi為輪齒所受的法向載荷;rbk為內外齒輪基圓半徑,k=1,2;Wn為輪齒所受總載荷;Ci為內嚙合齒輪副的法向柔度;i為齒對序號;φi為齒廓的理論間隙角;E為齒輪材料的彈性模量;b為齒寬。

1.3 混合潤滑基本方程組

根據文獻[3]建立的濾波減速器混合潤滑模型,考慮等溫瞬態彈流問題,濾波減速器齒面為三維線接觸彈流潤滑,潤滑方程組如下[13-14]

(2)

式中:h、p分別為考慮粗糙峰接觸的油膜厚度和接觸壓力;u1、u2分別為兩接觸表面沿x向和y向的平均速度;ρ為潤滑油的密度;η為潤滑油的等效黏度。

在數值計算時,將式(2)中的相關量按照如下公式進行歸一化

式中:pH為最大赫茲接觸壓力;ρ0為潤滑油的環境密度;η0為潤滑油的環境黏度;a、b分別為齒面赫茲接觸橢圓的長、短軸。

考慮輪齒修形的膜厚方程為

h=f(x,y,t)+δ1(x,y,t)+δ2(x,y,t)+ve(x,y,t)

(3)

式中:δ1(x,y,t)、δ2(x,y,t)為表面粗糙度;ve(x,y,t)為接觸表面的彈性變形,表達式如下

(4)

摩擦力的計算分成潤滑油膜中由于潤滑劑內剪切引起的流體摩擦以及表面粗糙接觸處的干接觸摩擦或邊界膜摩擦兩部分。

根據Bair-Winer流變模型[15],有

(5)

式中:G∞為極限剪切彈性模量;τL為極限剪切應力。對于典型的礦物油,用Dyson經驗公式估算G∞和τL

(6)

(7)

(8)

在每一個節點上求解這個非線性方程,即可得到在整個求解域上的剪切應力分布τ(x,y),然后積分計算出流體膜內的摩擦力

(9)

表面粗糙接觸處的干接觸摩擦因數或邊界膜摩擦因數可以通過試驗測得,通常齒輪傳動界面邊界的摩擦因數處于0.07～0.15的范圍內。然后,根據接觸載荷進行積分,即可求得邊界摩擦力Fb。

每對齒上的摩擦力

F=Ff+Fb

(10)

摩擦因數

(11)

1.4 數值計算與分析

利用方程(2),根據初始壓力分布得到彈性變形的初始估計值,然后將原始間隙量代入膜厚方程,求得初始膜厚,再將初始膜厚代入雷諾方程即可求解所有節點的壓力。具體過程請參考文獻[3]。重復以上過程,直到得到壓力收斂解,達到收斂精度

(12)

在迭代過程中,壓力松弛因子ωp一般取0.005～0.3,在載荷大、膜厚小的情況下,ωp應取相對小的值;H0的修正因子ωh一般取0.001～0.01。

濾波減速器基本參數:齒輪模數為0.5 mm,壓力角為20°,雙聯齒輪齒數為107,齒寬為5 mm,輸出齒輪齒數為112,齒寬為6 mm,齒輪彈性模量為206 GPa,泊松比為0.3,密度為7 800 kg/m3,額定轉速為1 500 r/min,額定轉矩為80 N·m。

潤滑劑基本參數:初始黏度η0=0.095 Pa·s,黏壓系數α=1.82×10-8Pa-1。計算邊界為-3.1≤X≤1.5,-1.1≤Y≤1.1,網格劃分為256×256。輪齒表面粗糙度采用實際測量數據,兩表面復合粗糙度均方根為0.5 μm。

根據上述參數計算得到不同轉速對應的嚙入點的摩擦因數、齒面膜厚分布及接觸面積比,如圖2所示。從圖中可以看出,隨著轉速的增大,嚙入點的平均油膜厚度增大,齒面接觸面積比下降,直接導致摩擦因數下降。

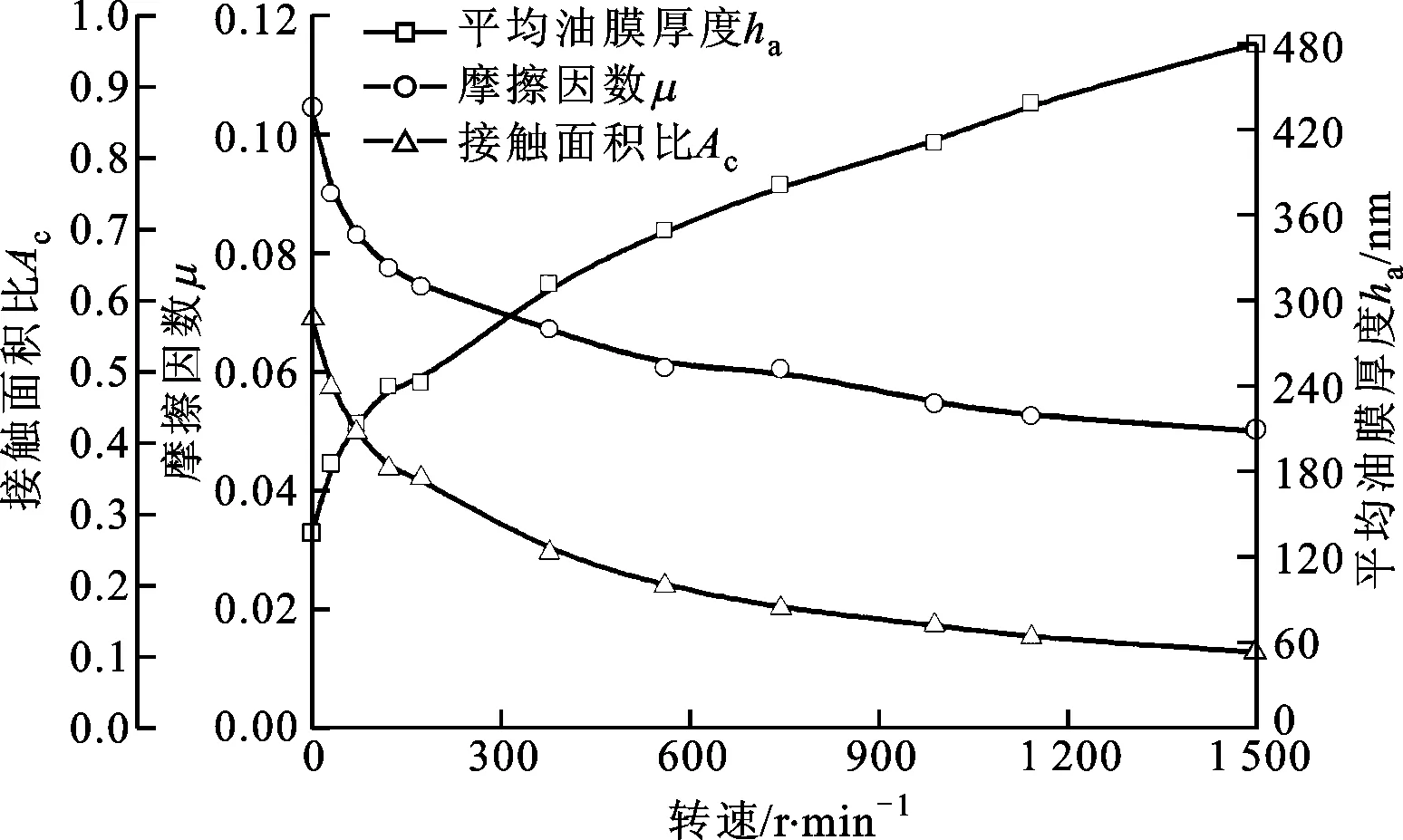
圖2 轉速對輸出齒輪嚙入點潤滑狀態的影響

2 濾波減速器的修形方法與嚙合沖擊

2.1 齒廓修形模型

合適的齒廓修形可以提高齒輪傳動的平穩性[16]。根據需要,對濾波減速器齒輪嚙合對中的雙聯齒輪Z1和輸出齒輪Z2進行齒頂修緣[17],修形原理模型如圖3所示。

圖3 齒廓修形示意圖

根據濾波減速器齒輪的低速輕載工況(輸入轉速為60 r/min,負載轉矩為80 N·m),采用拋物線修形曲線確定修形量

(13)

式中:Δ為最大修形量;x為修形曲線上的點沿嚙合線方向至修形起點的距離;l為修形長度。輪齒綜合最大變形量即為最大修形量,計算過程請參考文獻[18]。計算得到濾波減速器的理想齒廓修形參數:雙聯外齒輪最大修形量為30 μm,輸出內齒輪最大修形量為46 μm。

雙聯外齒輪Z1的修形起點K1處的半徑rK1=28.225 mm;輸出內齒輪Z2的修形起點K2處的半徑rK2=26.518 mm。齒輪副輸出內齒輪的修形公式為

(14)

齒輪副雙聯外齒輪的修形公式為

(15)

建立雙聯齒輪和輸出齒輪的單齒對齒廓修形三維模型,其正視圖見圖4。

圖4 單齒對理想齒廓修形模型正視圖

2.2 動力學仿真

圖5 濾波減速器有限元模型

根據減速器的參數,運用Abaqus軟件建立濾波減速器有限元模型(如圖5所示),并進行顯式動力學分析。為了便于分析,在Abaqus中對濾波減速器零部件進行了簡化處理,將行星架設為剛體,將固定齒輪、雙聯齒輪、輸出齒輪設為柔性體。行星架和雙聯齒輪之間為無摩擦接觸,其他齒輪間為有摩擦接觸(摩擦因數為μ)。使用六面體網格掃掠法對模型進行網格劃分,為了提高計算效率和計算精度,只對減速器輪齒上的網格進行加密,網格大小為0.1 mm,其他部位用較粗的網格。在偏心軸上添加輸入轉速n,輸出齒輪上添加轉矩負載80 N·m,設置分析步為6 s。

3 結果與討論

3.1 齒面摩擦對濾波減速器嚙合沖擊的影響

在進行理想修形后,分析齒面摩擦對濾波減速器動力學性能的影響。在n=60 r/min的工況下,分別以齒面摩擦因數μ=0.090 5和無摩擦接觸兩種情況進行仿真,分析齒面摩擦對輸出齒輪角加速度、輸出齒輪嚙入點接觸應力和輸出齒輪嚙入時齒面接觸力分布狀態的影響。圖6所示為濾波減速器穩定后行星架旋轉一周的輸出齒輪角加速度變化曲線,圖7為分析步周期內輸出齒輪嚙入點接觸應力的變化曲線,圖8為濾波減速器穩定后輸出齒輪嚙入時齒面接觸力的分布云圖。

圖6 摩擦因數對輸出齒輪角加速度的影響

圖7 摩擦因數對輸出齒輪嚙入點接觸應力的影響

(a)無摩擦時的嚙合區接觸力分布

(b)摩擦因數為0.090 5時的嚙合區接觸力分布圖8 摩擦因數對輸出齒輪嚙入時接觸力分布狀態的影響

從圖6～圖8可以看出:齒面摩擦對濾波減速器的動力學性能有明顯的影響。齒面摩擦的存在使輸出齒輪的角加速度降低了約33%,而對于嚙入點接觸應力,有摩擦較無摩擦的情況降低了約25%。可見,齒面摩擦對濾波減速器的動力學性能有顯著影響。因此,在動力學分析中,齒面摩擦的因素不可或缺。

對于實際工況,以潤滑油膜為介質的齒面摩擦能夠起到阻尼的作用,明顯減小接觸應力,降低濾波減速器的振動,緩解濾波減速器的嚙合沖擊。

3.2 齒廓修形量對濾波減速器嚙合沖擊的影響

為研究不同的齒廓修形量對濾波減速器動力學性能的影響,考慮表1所示的4組不同修形量,建立濾波減速器有限元模型。

表1 4組齒輪對修形量

根據濾波減速器的工況(輸入轉速為60 r/min,負載轉矩為80 N·m)及在此工況下的齒面潤滑情況(摩擦因數μ=0.090 5),對濾波減速器有限元模型進行動力學分析,結果如圖9～圖11所示。

圖9 修形量對輸出齒輪角加速度的影響

圖10 修形量對輸出齒輪嚙入點接觸應力的影響

圖9及圖10顯示:經過理想修形的濾波減速器可以明顯降低輸出齒輪的角加速度(降低約58%)和嚙入點接觸應力(降低約20%);過小或過大的修形量并不能有效改善濾波減速器的動力學性能。

從圖11a可以看出,齒面的異常接觸使有限單元扭曲,即嚙入點的嚴重干涉導致嚙入沖擊,說明在未修形的濾波減速器運轉過程中會出現較嚴重的齒輪干涉,這在實際情況下會導致濾波減速器“卡死”,使減速器傳動失效。從圖11c可以看出,進行了理想修形(46 μm)的濾波減速器沒有出現嚙合干涉區域,改善了齒面接觸情況,說明了理想修形的正確性。

3.3 不同潤滑狀態下濾波減速器的嚙合沖擊分析

在不同的潤滑狀態下,不同的轉速導致濾波減速器具有不同的齒面摩擦因數。因此,在分析不同轉速的濾波減速器有限元模型時,需考慮齒面摩擦因數對濾波減速器動力學特性的影響,以研究減速器在不同潤滑狀態下的修形效果。

不同濾波減速器轉速對應的摩擦因數見表2,在此基礎上分析不同潤滑狀態對齒輪嚙合沖擊的影響。圖12～圖14分別為不同轉速(潤滑狀態)對應的輸出齒輪角加速度變化曲線、輸出齒輪嚙入點的接觸應力變化曲線以及輸出齒輪嚙入時的齒輪接觸力分布云圖。

(a)未修形

(b)修形量為20 μm

(c)修形量為46 μm

(d)修形量為70 μm圖11 修形量對輸出齒輪嚙入時齒輪接觸力分布的影響

n/r·min-13060100150μ0.10420.09050.08570.0817

圖12 轉速(潤滑狀態)對輸出齒輪角加速度的影響

圖13 轉速(潤滑狀態)對輸出齒輪嚙入點接觸應力的影響

從圖12～圖14可以看出:在轉速較低的情況下,濾波減速器的振動沖擊并不明顯,而當輸入轉速達到100 r/min之后,經過修形的濾波減速器并不能完全消除嚙合沖擊;輸出齒輪的角加速度隨轉速增大而增大;齒面接觸狀態變差,除轉速為60 r/min時的情況外,其他轉速下齒面都出現了嚙入點干涉現象。圖13與文獻[6]的結果并不一致,說明齒面摩擦的影響不很明顯,齒面的接觸應力會隨著轉速提高而變大,這與文獻[19]的結論是一致的。

4 結 論

(1)基于濾波減速器齒輪的精確幾何模型,將真實的齒面形貌引入到齒輪混合潤滑模型中,深入探討了混合潤滑狀態下齒面摩擦因數的計算方法,計算結果顯示,減速器齒面的摩擦因數隨轉速增大而減小,這對濾波減速器的傳動效率研究具有重要意義。

(2)分析了齒面摩擦因數對濾波減速器動力學性能的影響,結果表明潤滑油膜的存在可明顯改善濾波減速器的動力學性能,因此,在濾波減速器的修形與嚙合沖擊研究中齒面摩擦因素不可或缺。

(a)轉速為30 r/min

(b)轉速為60 r/min

(c)轉速為100 r/min

(d)轉速為150 r/min 圖14 轉速(潤滑狀態)對輸出齒輪嚙入時齒輪接觸力分布的影響

(3)將真實工況下的齒面潤滑狀況引入到濾波減速器的有限元模型,在動力學范疇內分析研究了不同齒廓修形量對減速器嚙合沖擊及齒面接觸狀態的影響規律;針對設定的濾波減速器工況的分析結果表明,理想的齒廓修形可以明顯改善濾波減速器的動力學性能,當輸出齒輪修形量為46 μm、雙聯齒輪修形量為30 μm時動力學性能最好,而過小、過大的修形量并不能達到改善減速器動力學性能的目的。

(4)不同的潤滑狀態對濾波減速器的嚙合沖擊有較大的影響,在寬轉速范圍內的濾波減速器動力學性能與轉速成負相關關系,這一結果對修形濾波減速器的工況選擇應具有指導意義。

[1] 王家序, 肖科, 李俊陽, 等. 濾波減速器: 中國, CN 201010104359.5 [P]. 2011-03-15.

[2] REN Ning, ZHU Dong, CHEN W W, et al. A three-dimensional deterministic model for rough surface line-contact EHL problems [J]. Journal of Tribology, 2009, 131(1): 1-9.

[3] 蒲偉, 王家序, 李俊陽, 等. 齒向修形對濾波減速器潤滑性能的影響分析 [J]. 摩擦學學報, 2014, 34(4): 393-399. PU Wei, WANG Jiaxu, LI Junyang, et al. Analysis of longitudinal modification on lubrication performance of filtering reducer [J]. Tribology, 2014, 34(4): 393-399.

[4] 張有忱. 齒輪齒面摩擦系數變化的研究 [J]. 潤滑與密封, 1990(5): 22-25. ZHANG Youchen. Study of the variation in the coefficient of friction on surfaces on gear teeth [J]. Lubrication Engineering, 1990 (5): 22-25.

[5] 周哲波. 彈流潤滑狀態下齒輪嚙合效率的研究 [J]. 機械設計, 2004, 21(12): 40-43. ZHOU Zhebo. Study on gear meshing efficiency under condition of elasto-hydrodynamic lubrication [J]. Journal of Machine Design, 2004, 21(12): 40-43.

[6] 馮海生, 王黎欽, 鄭德志, 等. 計及齒面摩擦的高功率密度齒輪傳動效率分析 [J]. 華南理工大學學報: 自然科學版, 2014, 42(9): 24-29. FENG Haisheng, WANG Liqin, ZHENG Dezhi, et al. Analysis on high power density gear transmission efficiency considering tooth friction [J]. Journal of South China University of Technology: Natural Science Edition, 2014, 42(9): 24-29.

[7] 盧立新, 闕師鵬, 蔡瑩, 等. 齒輪幾何參數對齒輪傳動彈流潤滑性能的影響 [J]. 機械傳動, 1998, 22(1): 25-28, 53. LU Lixin, QUE Shipeng, CAI Ying, et al. Influence of gear geometry factors on the elasto-hydrodynamic lubrication properties of a gear transmission [J]. Mechanical Transmission, 1998, 22(1): 25-28, 53.

[8] 盧立新, 蔡瑩. 直齒輪傳動非牛頓流體瞬態彈流潤滑研究 [J]. 潤滑與密封, 2005(6): 36-38. LU Lixin, CAI Ying. Transient non-Newtonian elasto-hydrodynamic lubrication of spur gear transmission [J]. Lubrication Engineering, 2005(6): 36-38.

[9] 周長江, 唐進元, 鐘志華. 齒輪傳動的線外嚙合與沖擊摩擦 [J]. 機械工程學報, 2008, 44(3): 75-81. ZHOU Changjiang, TANG Jinyuan, ZHONG Zhihua. Corner contact and impact friction of gear drive [J]. Chinese Journal of Mechanical Engineering, 2008, 44(3): 75-81.

[10]劉文吉, 宋朝省, 洪英. NN型少齒差行星齒輪傳動嚙合沖擊分析及修形設計 [J]. 中國機械工程, 2012, 23(4): 425-429. LIU Wenji, SONG Chaosheng, HONG Ying. Meshing impact analysis and profile modification of planetary gear drive with small tooth number difference [J]. China Mechanical Engineering, 2012, 23(4): 425-429.

[11]李諍. 考慮齒面摩擦非線性影響的直齒輪齒根動應力分析 [J]. 艦船科學技術, 2013, 35(10): 82-87. LI Zheng. Research on dynamic tooth root stress of spur gear with the consideration of nonlinear friction influence [J]. Ship Science and Technology, 2013, 35(10): 82-87.

[12]SHU Xiaolong. Determination of load sharing factor for planetary gearing with small tooth number difference [J]. Mechanism and Machine Theory, 1995, 30(2): 313-321.

[13]朱才朝, 黃健, 唐倩. 少齒差行星齒輪傳動實際接觸齒數及載荷分配的研究 [J]. 中國機械工程, 2002, 13(18): 1586-1589. ZHU Caichao, HUANG Jian, TANG Qian. Study on contact teeth and load distribution of planetary gear with small tooth number difference [J]. China Mechanical Engineering, 2002, 13(18): 1586-1589.

[14]ZHU Dong, WANG Jiaxu, REN Ning, et al. Mixed elastohydrodynamic lubrication in finite roller contacts involving realistic geometry and surface roughness [J]. Journal of Tribology, 2012, 134(1): 1-10.

[15]ZHU Dong, CHENG H S. An analysis and computational procedure for EHL film thickness, friction and flash temperature in line and point contact [J]. Tribology Transactions, 1989, 32(3): 364-370.

[16]張展. 齒廓修形和齒向修形 [J]. 建筑機械, 1987(10): 35-39. ZHANG Zhan. Profile modification and axial modification [J]. Construction Machinery, 1987(10): 35-39.

[17]李潤方. 齒輪傳動的剛度分析和修形方法 [M]. 重慶: 重慶大學出版社, 1998: 153-161.

[18]張永忠. 關于修形齒輪的計算方法 [J]. 煤礦機械, 1984(2): 2-6. ZHANG Yongzhong. The calculation method of modification gear [J]. Coal Mine Machinery, 1984(2): 2-6.

[19]姚文席. 修形漸開線直齒輪的嚙合沖擊研究 [J]. 北京機械工業學院學報, 2000, 15(2): 1-4, 18. YAO Wenxi. The study of mesh impact in the transmission of modified spur gear [J]. Journal of Beijing Institute of Machinery, 2000, 15(2): 1-4, 18.

[本刊相關文獻鏈接]

陳兵奎,梁棟,彭帥,等.共軛曲線齒輪嚙合管齒面的幾何及接觸特性分析[J].2015,49(3):85-94.[doi:10.7652/xjtuxb 201503015]

陶慶,孫文磊,周建星.考慮齒圈柔性的行星傳動系統固有特性與靈敏度研究[J].2015,49(3):113-120.[doi:10.7652/xjtuxb201503018]

蔣進科,方宗德,蘇進展.寬斜齒輪多目標修形優化設計[J].2014,48(8):91-97.[doi:10.7652/xjtuxb201408016]

鄒創,陶濤,梅雪松,等.機器人關節短筒諧波減速器接觸計算與分析[J].2013,47(5):82-87.[doi:10.7652/xjtuxb2013 05015]

宋朝省,朱才朝,劉立斌.船用交錯軸變厚齒輪嚙合性能的研究[J].2012,46(11):64-68.[doi:10.7652/xjtuxb201211013]

鄧星橋,向中凡,王進戈.加工和安裝誤差對無側隙蝸桿傳動接觸線及齒廓的影響[J].2011,45(2):111-116.[doi:10.7652/xjtuxb201102023]

馮詩愚,高秀峰,劉衛華,等.內嚙合擺線轉子壓縮機型線連續性條件研究[J].2009,43(1):34-37.[doi:10.7652/xjtuxb 200901008]

吳偉烽,馮全科,徐健.單螺桿壓縮機齒型的多圓柱包絡原理[J].2007,41(11):1271-1274.[doi:10.7652/xjtuxb200711 005]

馮詩愚,高秀峰,劉衛華,等.內嚙合轉子壓縮機齒間嚙合效率研究[J].2007,41(9):1040.[doi:10.7652/xjtuxb200709 008]

(編輯 葛趙青)

Study on Meshing Impact and Modification Method of Filtering Reducer Considering Mixed Lubrication

CHU Kunming1,WANG Jiaxu1,2,3,PU Wei2,ZHOU Guangwu2,ZHANG Ying1

(1. School of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065, China;2. School of Aeronautics and Astronautics, Sichuan University, Chengdu 610065, China; 3. Institute of Mechanical and Electrical Transmission and Transport Equipment, Chongqing University, Chongqing 400044, China)

For analyzing the meshing impact of filtering reducers, the elastohydrodynamic lubrication (EHL) of the reducer in actual working condition is studied considering the rotational speed, load and real tooth surface roughness. A mixed lubrication model is established to calculate the lubrication status at the engaging-in position under different rotational speeds with suggested calculation method of friction coefficient. Taking actual working condition into account, the method of tooth profile modification (TPM) is suggested with the reducer’s finite element model established based on the study of EHL to analyze the effects of friction coefficient of tooth surface, TPM, and lubrication status on the meshing impact. It is found that the friction coefficient will reduce with the rotational speed under mixed lubrication. Compared with frictionless contact, frictional contact can significantly weaken meshing impact and improve gear contact status, thus the friction coefficient of tooth surface must be considered in the study of filtering reducer meshing impact. FEM analysis shows that the optimized TPM amount for output-gear and dual-gear is 46 μm and 30 μm, respectively, whereby the dynamic characteristics of filtering reducer are significantly improved, whereas too small or too large TPM amount will not effectively weaken the meshing impact. Moreover, lubrication status has also obvious influence on the meshing impact, but the influence of tooth surface friction is less obvious, in contrast, higher rotational speed will lead to deterioration of the dynamic characteristics.

filter reducer; mixed lubrication; tooth profile modification; finite element; meshing impact

2014-12-15。

褚坤明(1989—),男,碩士生;王家序(通信作者),男,教授,博士生導師。

國家自然科學基金資助項目(51435001,51375506);重慶市“兩江學者”計劃專項經費資助項目;中央高校基本科研業務費專項資金資助項目(2014SCU11009)。

時間:2015-04-29

10.7652/xjtuxb201507023

TH132

A

0253-987X(2015)07-0140-09

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150429.1437.007.html