機動飛行下擠壓油膜阻尼器對碰摩故障轉子系統的影響

張俊紅,馬梁,魯鑫,王俊,林杰威

(1.天津大學內燃機燃燒學國家重點實驗室,300072,天津;2.天津大學仁愛學院,300000,天津;3.英國南安普頓大學振動噪聲學院,SO17 1BJ,英國南安普頓)

?

機動飛行下擠壓油膜阻尼器對碰摩故障轉子系統的影響

張俊紅1,2,馬梁1,2,魯鑫1,王俊2,林杰威3

(1.天津大學內燃機燃燒學國家重點實驗室,300072,天津;2.天津大學仁愛學院,300000,天津;3.英國南安普頓大學振動噪聲學院,SO17 1BJ,英國南安普頓)

飛機飛行時,航空發動機的故障對于飛機的安全性有著重要影響。針對這個問題,基于Lagrange方程,建立了飛機在空間進行機動飛行時發動機轉子系統的動力學模型;同時基于庫倫定律,建立了轉子碰摩故障模型;基于雷諾方程,建立了擠壓油膜阻尼器的模型;對模型進行綜合建模,得到不同機動飛行條件下轉子-滾動軸承-擠壓油膜阻尼器(SFD)系統非線性動力學微分方程,通過龍格庫塔數值解法進行求解得到不同機動飛行狀態下碰摩故障狀態的系統振動響應,得到了不同機動飛行狀態下碰摩故障轉子系統的運動分岔圖,同時利用典型轉速(1 400 rad/s,2 000 rad/s)下轉子系統的頻譜圖、龐加萊圖、時域圖和軸心軌跡圖研究系統的動力學特性。研究結果表明:在高轉速下,SFD能夠顯著提高系統的穩定性,抑制系統的非線性特征,但是在低轉速下可能損害系統穩定性;不同機動飛行狀態下,SFD對于轉子系統非線性特征的影響大小也不同。

轉子-滾動軸承系統;機動飛行;碰摩故障;擠壓油膜阻尼器

擠壓油膜阻尼器(SFD)對軸承有著顯著的減振效果,且結構簡單,制造簡便,故廣泛應用于航空發動機的振動控制中[1]。SFD特性對轉子系統動力學行為的影響一直是轉子動力學領域的一個重要課題。碰摩故障是航空發動機運行過程中常見的故障,對航空發動機的整機振動性能和安全性有著重要的影響。目前國內外許多專家學者對于碰摩故障機理有著較深的研究,但研究主要集中于靜止狀態下碰摩故障對轉子系統動力學特性的影響,對于機動飛行狀態下碰摩故障轉子系統動力學行為的研究較少。

孟光等對帶擠壓油膜軸承Jeffcott轉子系統的油膜機理以及系統動力學特性等進行了全面的研究,提出系統在獲得最小振幅的同時也得到了較好的傳遞率參數組合[2-3];Moraru等建立帶雙間隙SFD的轉子動力學模型,并且通過數值模擬方法研究阻尼器的振動特性[4-5];周海侖等通過仿真和實驗對比,研究浮環擠壓油膜阻尼器的振動特性[6]。但是,以上研究都是建立在轉子系統靜止基礎平臺狀態下,而實際中航空發動機是在機動飛行條件下運行,在此情況下轉子系統會受到附加激勵力的作用。祝長生根據Lagrange方程建立了飛機在任意空間機動飛行時發動機任意位置條件不平衡多盤、質量和軸承線性及非線性柔性轉子系統動力學的統一模型,并研究轉子在機動飛行下的動力學響應[7-8],但未考慮SFD的作用;徐敏等研究了機動飛行條件下Jeffcott轉子以及帶擠壓油膜阻尼器轉子的振動特性[9-11],但并未考慮碰摩故障。

本文在文獻[8]的基礎上,研究了SFD在不同機動飛行條件下對碰摩故障轉子系統動力學行為的影響。

1 系統模型與基本理論

1.1 轉子動力學微分方程

航空發動機轉子試驗臺模型可簡化為如圖1所示的轉子-軸承-SFD系統,mrp、mbl、ms分別為盤的集中質量、軸在軸承處的集中質量、軸承外圈質量;crp、cbl為盤的阻尼系數和阻尼器處的阻尼系數;kp、ka、kr為軸的剛度、支承剛度和碰摩剛度;e為盤的偏心距。整個系統在靜止基礎平臺狀態下的運動微分方程為

(1)

式中:Ω為轉子轉動角速度;Frx、Fry為轉子碰摩故障力;Fblx、Fbly為滾動軸承支反力;Fsx、Fsy為擠壓油膜阻尼器的油膜力。

圖1 轉子-軸承系統簡化模型

1.2 轉子在機動飛行條件下的運動方程

當航空發動機在機動飛行條件下運行時,發動機輪盤會產生附加激勵力,對系統性能有重要的影響,在這里不考慮機動飛行對于軸承和擠壓油膜阻尼器的影響,僅探討機動飛行對于盤的影響。

1.2.1 機動飛行下飛機坐標系 一般來說,飛機的發動機常常安裝在機身或機翼上,坐標系如圖2所示。飛機繞x軸的運動稱之為俯仰運動,繞z軸的運動稱之為橫滾運動,繞y軸的運動稱之為盤旋運動。

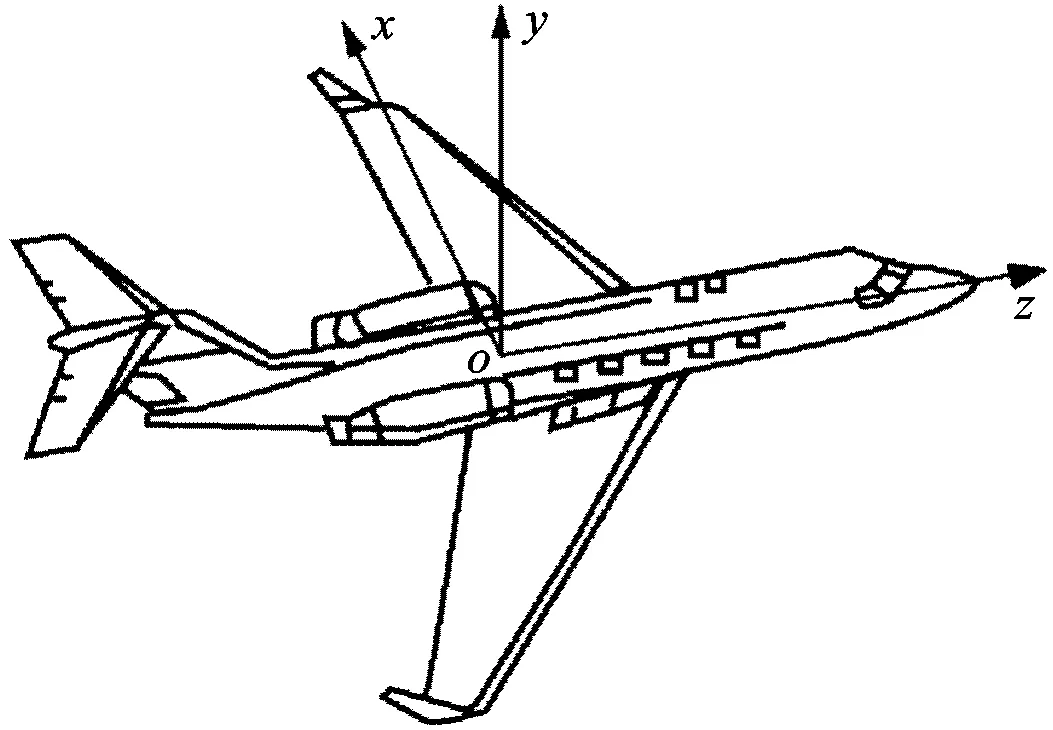
圖2 飛機機動飛行時的坐標系

在對轉子進行分析時,采用地面固定坐標系、機體相對坐標系和轉子坐標系這3個坐標系來表示機體和轉子的空間狀態,如圖3所示。

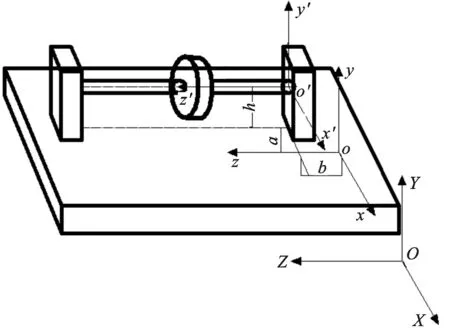
圖3 轉子坐標系統示意圖

圖3中OXYZ坐標系位于地面,表示飛機的空間飛行狀態,坐標系oxyz位于機體上,表示飛機自身的轉動特性,坐標系o′x′y′z′位于轉子上,表示與機體坐標系平行。

1.2.2 系統運動方程的推導 由圖2可知,飛機在飛行時,運動可分為沿x、y、z軸的3個平動[vx,vy,vz],以及繞3個軸的轉動[ωx,ωy,ωz],輪盤的動能由平動和轉動動能組成,即

(2)

式中:T為盤總動能;Tt為盤的平動動能;Tr為盤的轉動動能。

設盤在xy平面內轉動時相對于轉子坐標系的位移為[xrp,yrp](軸向位移忽略不計),則可推知盤的平動動能為

(3)

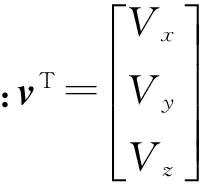
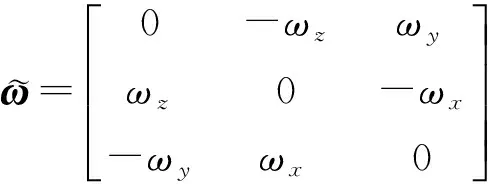
為便于計算,將盤繞ox、oy、oz軸的轉動角速度用歐拉角表示,設φ、φ、γ為轉子繞ox、oy、oz軸的轉角,則旋轉角速度為

(4)

設歐拉角是小量,則盤的轉動動能為

(5)

式中:θx、θy為柔性軸繞oxyz坐標系的轉動角;Id、Ip為盤的直徑轉動慣量和極轉動慣量。

根據Lagrange方程對圓盤的動能求導,可得圓盤在機動飛行條件下的運動微分方程為

(6)

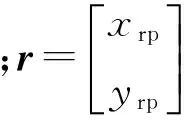
1.3 轉子故障模型

假定轉子已處于碰摩狀態,由于碰撞發生的時間間隔非常短,可假設碰撞時定子的變形為線性變形,轉子與定子的摩擦符合庫侖定律[12-13],如圖4所示。

圖4 輪盤碰摩示意圖

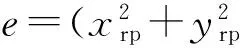
(7)

式中:kr為碰摩剛度;f為摩擦系數。

將碰摩力分解為

(8)

1.4SFD油膜力模型

SFD的油膜力計算可以根據流體動壓潤滑理論求得,依據雷諾方程可以導出SFD油膜壓力的分布,SFD的瞬態雷諾方程為[14]

(9)

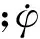
根據短軸承理論和π油膜假設,可以推導出SFD的油膜力[15-16]為

(10)

式中:L為軸頸長度;c為油膜間隙;ε為軸頸偏心率。求得油膜力在x、y方向上的分量為

(11)

1.5 滾動軸承模型

本研究所用的滾動軸承為深溝球軸承,由外圈、內圈、滾動體和保持架組成,如圖5所示。設軸承中滾珠在內外滾道之間等距排列,滾珠與滾道之間為純滾動,設滾珠與外圈接觸點線速度為vo,與內圈接觸點線速度為vi,軸承外圈旋轉角速度為ωo,內圈旋轉角速度為ωi,外滾道半徑為Ro,內滾道半徑為Ri,則有vo=ωoRo,vi=ωiRi。

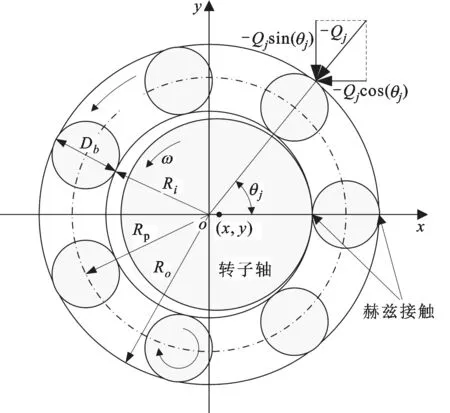
圖5 滾動軸承模型示意圖

(12)

設內圈中心的振動位移為x、y,軸承間隙為Δr,則第j個滾珠與滾道之間的接觸變量δj=xcosθj+ysinθj-Δr,只有δj>0才有作用力,根據赫茲接觸理論可得

(13)

式中:Cb為赫茲接觸剛度;H為亥維賽函數;Fi在x、y方向上的分量為

(14)

故滾動軸承產生的軸承力為

(15)

1.6 模型計算參數

根據以上模型建立微分方程,設置系統參數初始值,運用龍格庫塔數值解法進行求解。系統各個部分的參數如表1、表2、表3所示。

表1 轉子系統參數值

2 結果分析

飛機正常航行時,飛行速度、高度、方向這3個機動飛行參數在不斷變化,

同時伴隨一定的轉動運

表3 滾動軸承參數值

動。飛機在機動飛行條件下,轉子系統除受到自身的不平衡力之外,還受到機動飛行附加激勵力,這對系統的動力特性有著重要的影響。根據飛機實際飛行狀況,本研究選取起飛、水平盤旋、橫滾機動這3種具有代表性的飛行狀態,分別討論對轉子系統動力學響應的影響。

2.1 飛機起飛狀態下轉子動力響應分析

在起飛狀態下,對于無SFD的系統,當碰摩故障發生時,系統盤的集中質量節點在x方向上的位移隨轉速變化的分岔圖如圖6所示。當轉速在600～1 782 rad/s之間時,系統以周期1形式運動;當轉速到達1 783 rad/s時,系統發生跳躍,并在1 782～1 830 rad/s間以擬周期形式運動;當轉速在1 830～2 500 rad/s內,系統的主要運動形式是擬周期和混沌運動,并伴隨多倍周期運動,并且在1 970～2 015、2 184～2 224和2 426～2 456 rad/s內出現了擬周期分岔。由此可知,系統在中低轉速下運動形式較為穩定,但是當轉速大于1 782 rad/s時,系統運動出現混動擬周期形式。

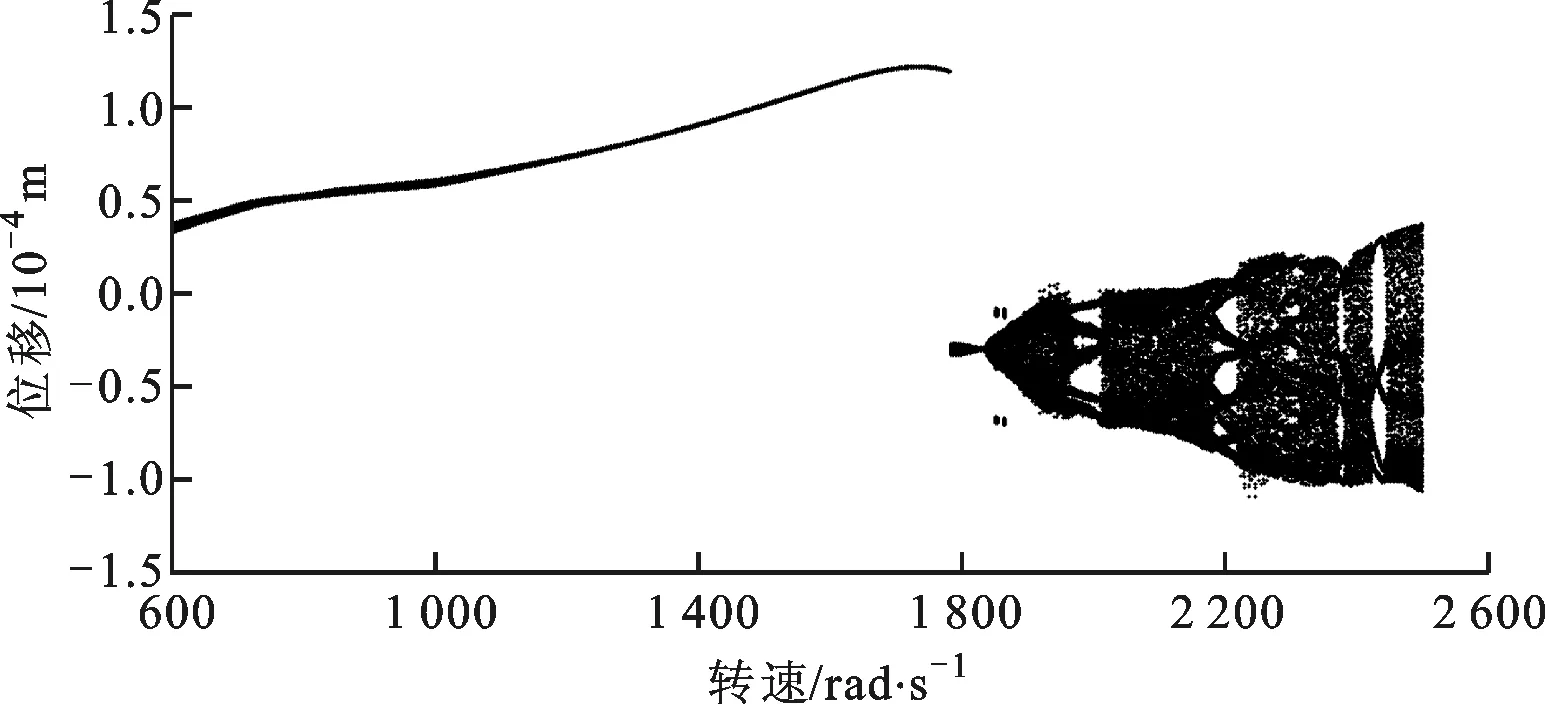
圖6 起飛狀態下碰摩故障-無SFD轉子位移響應分岔圖

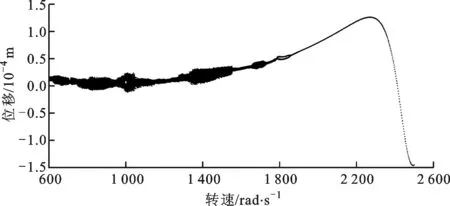
圖7 起飛狀態下碰摩故障-帶SFD轉子位移響應分岔圖

對于帶SFD的系統,在同樣條件下計算,可得系統盤的集中質量節點在x方向上位移隨轉速變化的分岔圖,如圖7所示。當轉速在600～1 560 rad/s時,系統以擬周期運動;在1 560～1 654 rad/s間以周期1形式運動;在1 654～1 735 rad/s間以擬周期運動;在1 735～1 788 rad/s間以周期1形式運動;在1 788 rad/s發生了分岔,并在1 788～1 868 rad/s以周期2形式運動;當轉速大于1 870 rad/s時,系統以周期1形式運動。

對典型轉速下的轉子運動形式分析可知:在1 400 rad/s下,由圖8b可知,無SFD碰摩故障下轉子系統以周期1形式運動,由圖8c可知,轉子系統以1倍頻為主,只有極小的2倍頻,軸心軌跡較為規則;由圖9b可知,系統以擬周期運動,從圖9c可知,系統不僅2倍頻增加,而且出現了一系列的分頻諧波,軸心軌跡出現了復雜的網狀結構。

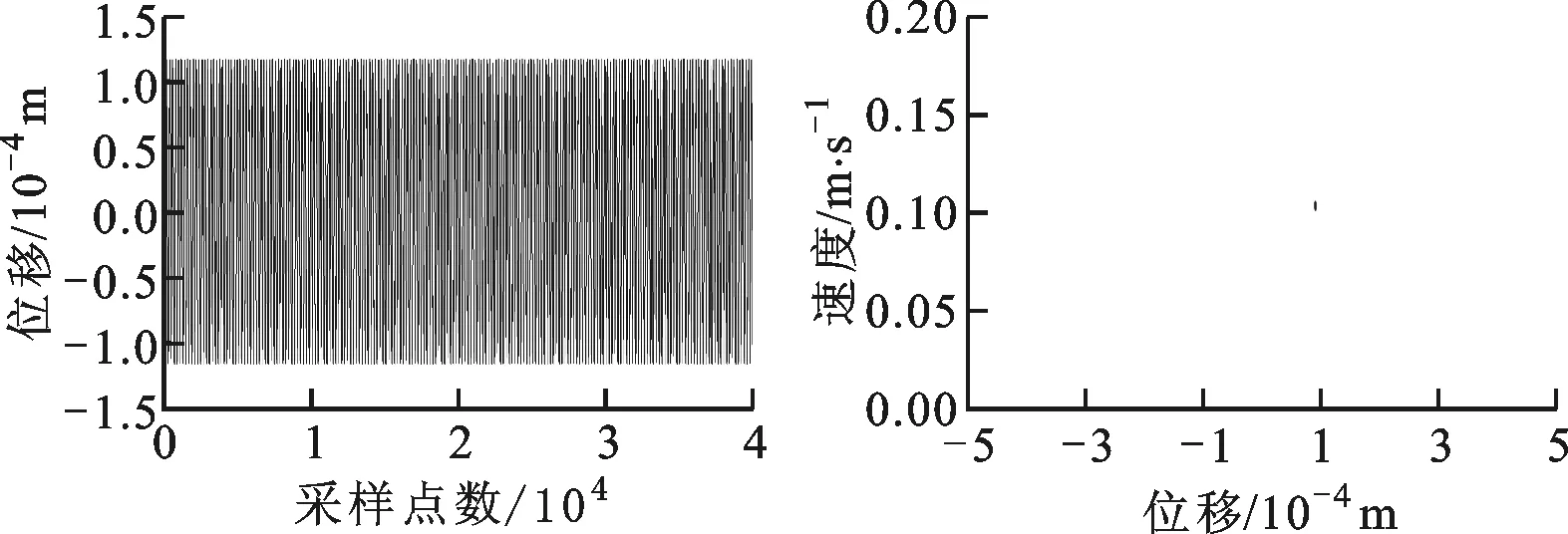
(a)時域圖 (b)龐加萊圖

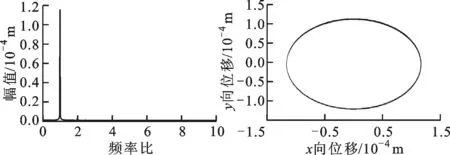
(c)頻譜圖 (d)軸心軌跡圖圖8 ω=1 400 rad/s時起飛狀態無SFD-碰摩故障轉子的系統圖

(a)時域圖 (b)龐加萊圖

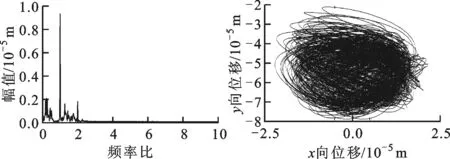
(c)頻譜圖 (d)軸心軌跡圖圖9 ω=1 400 rad/s時起飛狀態下帶SFD-碰摩故障轉子的系統圖

在轉速為2 000 rad/s時,由圖10可知,無SFD碰摩系統以擬周期運動,并且出現5條分岔路徑;系統出現了一系列分頻諧波,而軸心軌跡則出現復雜的網狀結構及碰摩折返現象;由圖11可知,帶SFD的碰摩轉子系統以周期1的形式運動,只有1倍頻,分頻量消失。由此可見,在起飛狀態下,SFD使得轉子系統在不同轉速下的動力學行為發生較大改變,其中在1 400 rad/s時,系統的頻譜成分更加豐富,運動軌跡更加復雜,但是在2 000 rad/s時,系統頻譜分量簡單,運動軌跡較為規則。

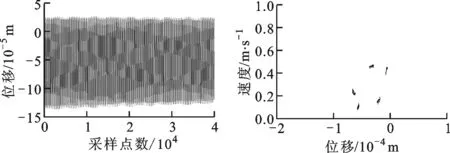
(a)時域圖 (b)龐加萊圖

(c)頻譜圖 (d)軸心軌跡圖圖10 ω=2 000 rad/s時起飛狀態下無SFD-碰摩故障轉子的系統圖

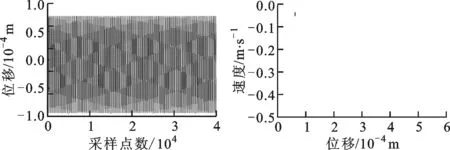
(a)時域圖 (b)龐加萊圖

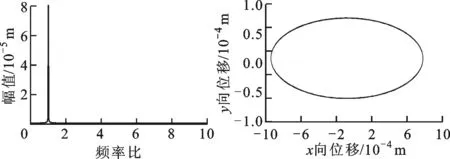
(c)頻譜圖 (d)軸心軌跡圖圖11 ω=2 000 rad/s時起飛狀態下帶SFD-碰摩故障轉子的系統圖

2.2 橫滾機動飛行狀態下轉子動力響應分析

在橫滾狀態下,對于無SFD-碰摩故障系統,系統盤的集中質量節點在x方向上的位移隨轉速變化的分岔圖如圖12所示。當轉速在600～760 rad/s時,系統為周期1運動;當轉速在760～1 032 rad/s時,系統為擬周期運動;當轉速在1 032 rad/s時,系統發生跳躍,并在1 032～1 928 rad/s內以周期1形式運動;當轉速到達1 928 rad/s時,系統發生跳躍,以倒分岔的形式在2 068 rad/s進入擬周期運動;轉速在2 068～2 500 rad/s時,系統主要以擬周期形式運動,中間出現多次分岔現象。

圖12 橫滾狀態下碰摩故障-無SFD轉子系統分岔圖

帶SFD-碰摩故障系統在橫滾機動飛行條件下的位移隨轉速變化的分岔圖如圖13所示。系統在中低轉速下以周期1的形式運動,656～772、1 308～1 432、1 484～1 572、1 740～1 936 rad/s內以擬周期形式運動,在1 936～2 500 rad/s內以周期1形式運動。

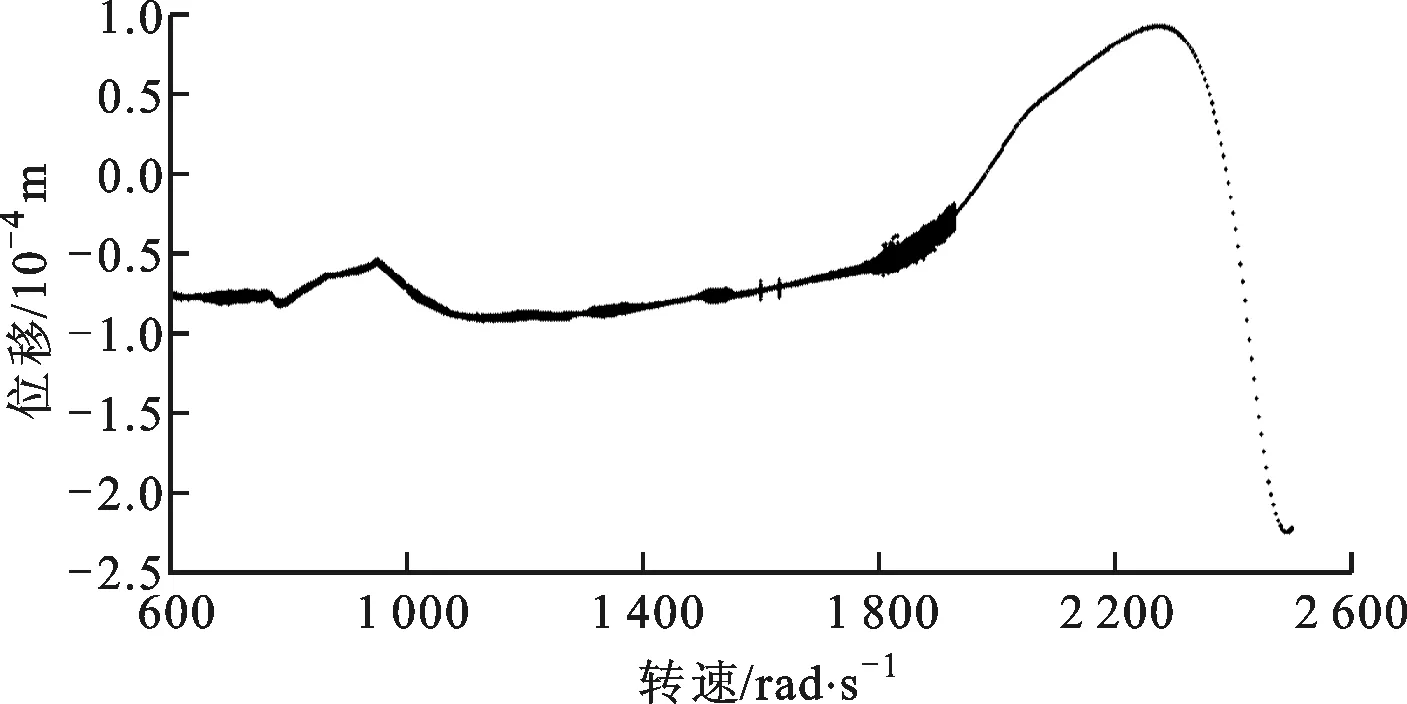
圖13 橫滾狀態下碰摩故障-帶SFD轉子系統分岔圖

(a)時域圖 (b)龐加萊圖

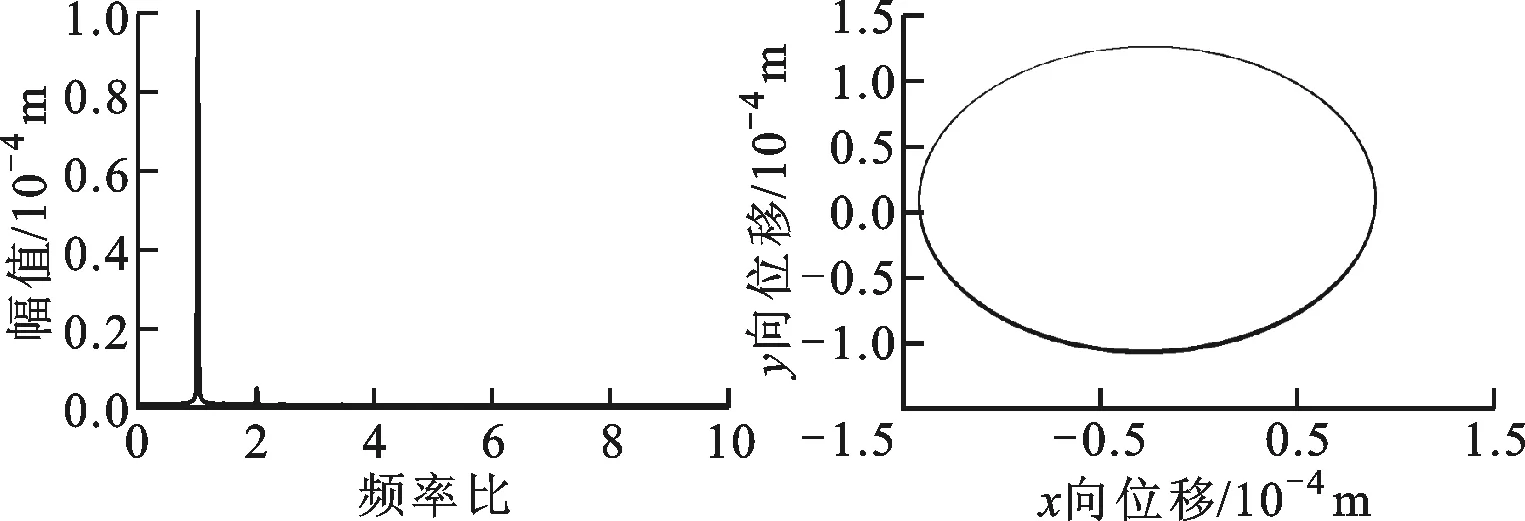
(c)頻譜圖 (d)軸心軌跡圖圖14 ω=1 400 rad/s時橫滾狀態下無SFD-碰摩故障轉子的系統圖

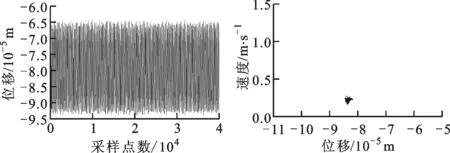
(a)時域圖 (b)龐加萊圖

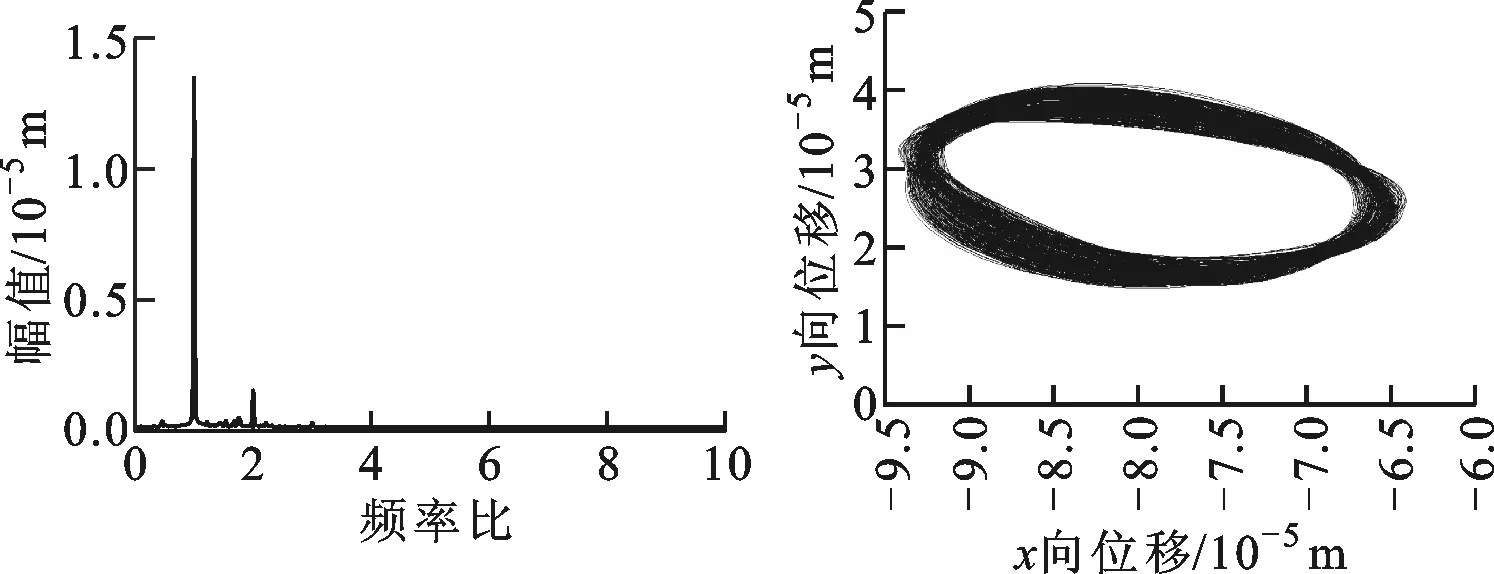
(c)頻譜圖 (d)軸心軌跡圖圖15 ω=1 400 rad/s時橫滾狀態下帶SFD-碰摩故障轉子的系統圖

當轉速為1 400 rad/s時,由圖14b可知,在橫滾狀態下,無SFD-碰摩故障轉子系統以周期1形式運動,由圖14c可知,系統除1倍頻外,出現較小的2倍頻,軸心軌跡較為規則,只有輕微的網狀結構,由圖15b可知,SFD-碰摩故障轉子系統以擬周期運動,圖15c中轉子系統2倍頻量增加,并且出現了微小的分頻量,在圖15d中系統軸心軌跡出現了明顯的網狀結構。

(a)時域圖 (b)龐加萊圖

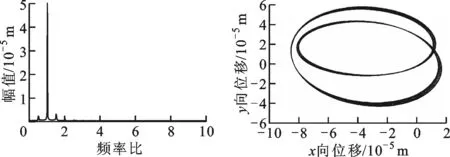
(c)頻譜圖 (d)軸心軌跡圖圖16 ω=2 000 rad/s時橫滾狀態下無SFD-碰摩故障轉子的系統圖

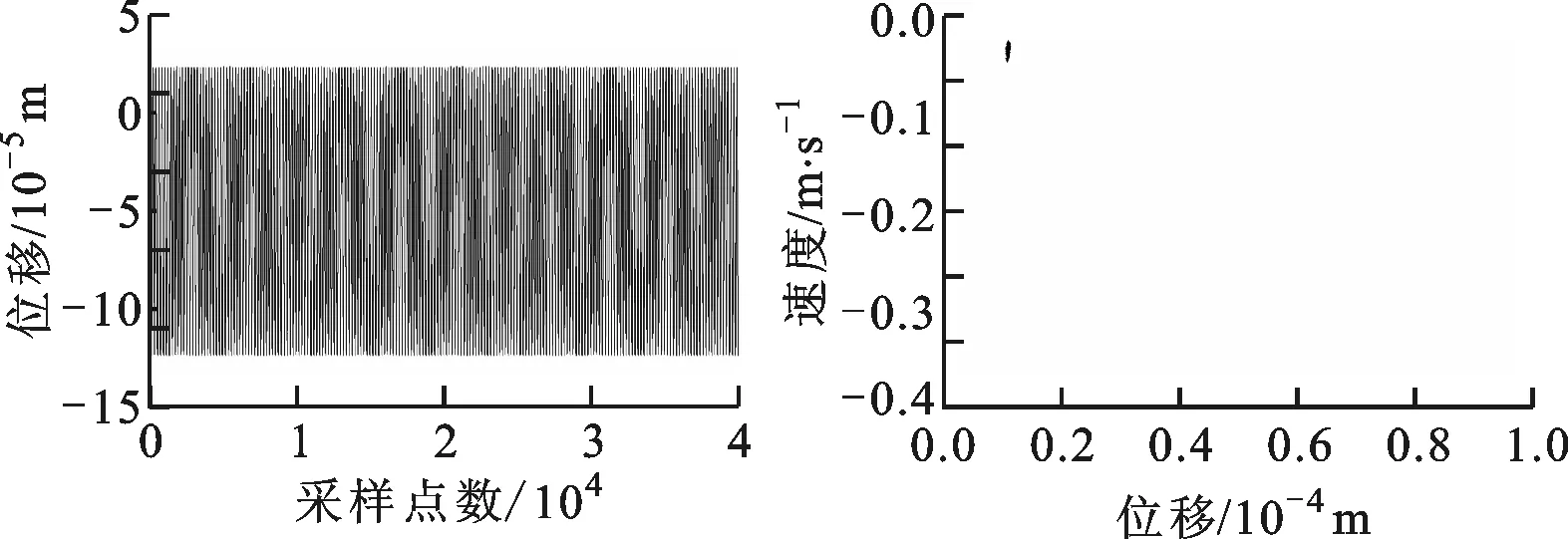
(a)時域圖 (b)龐加萊圖

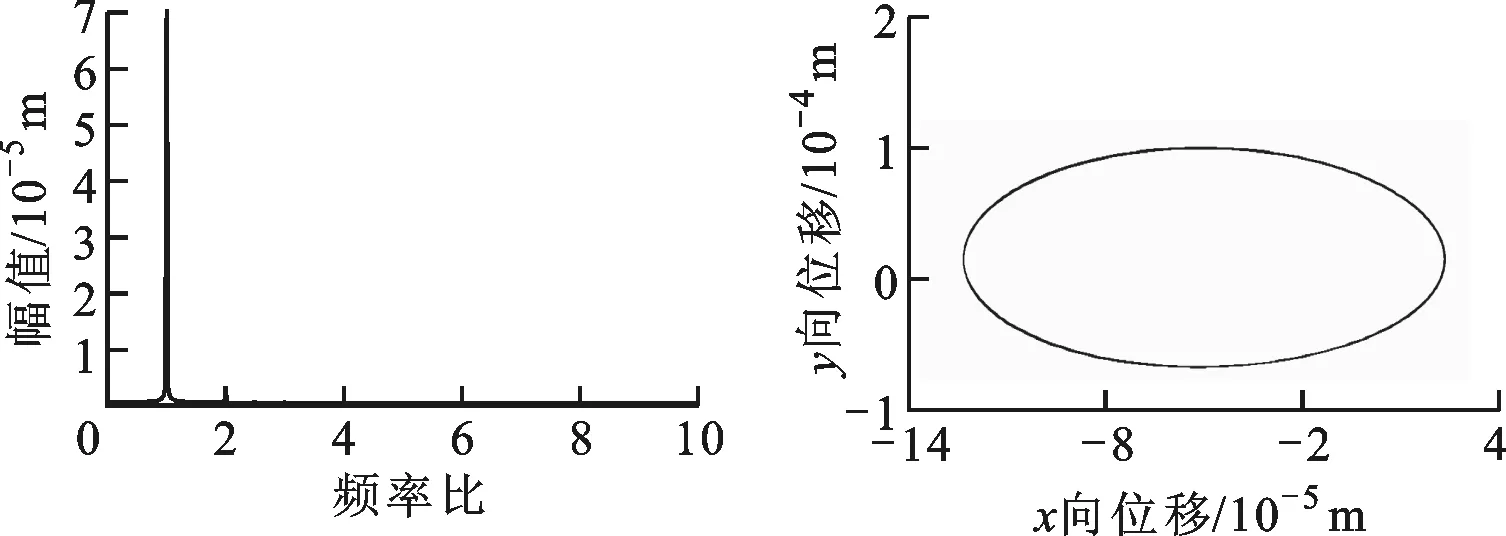
(c)頻譜圖 (d)軸心軌跡圖圖17 ω=2 000 rad/s時橫滾狀態下帶SFD-碰摩故障轉子的系統圖

當轉速為2 000 rad/s時,由圖16可知,無SFD-碰摩轉子系統以周期2形式運動,此時系統出現了分頻量,同時軸心軌跡出現不規則形狀;由圖17可知,同轉速下SFD-碰摩轉子系統以周期1形式運動,系統的分頻量已經消失,轉子軸心軌跡形狀規則。通過對比,SFD對于不同轉速下碰摩故障轉子系統的動力學行為有重要的影響,在1 400 rad/s時,頻譜成分和運動軌跡變復雜,但是相較于起飛狀態,對于轉子系統頻譜成分和運動軌跡的影響有所降低;在2 000 rad/s時,運動軌跡變規則,頻譜成分簡單。

2.3 飛機水平盤旋狀態下轉子動力響應分析

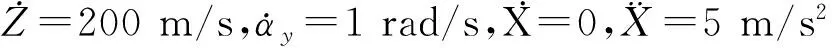
在水平盤旋狀態下,對于碰摩故障-無SFD轉子系統,系統盤的集中質量節點在x方向上的位移隨轉速變化的分岔圖如圖18所示。當轉速在600～950 rad/s時,系統為擬周期運動;當轉速在950～1 190 rad/s時,系統以周期1形式運動;當轉速在1 190～1 425 rad/s時,系統以擬周期形式運動;當轉速在1 425 rad/s時,系統發生了跳躍,并在1 425～1 975 rad/s內以周期1形式運動;系統在1 975 rad/s時發生分岔,在1 975～2 155 rad/s內以周期2形式運動;此后系統進入擬周期。

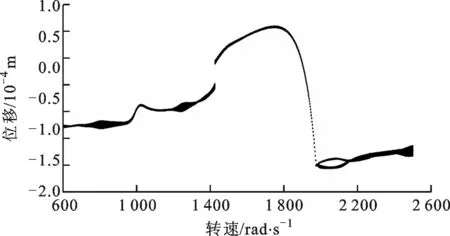
圖18 水平盤旋狀態下碰摩故障-無SFD轉子系統分岔圖

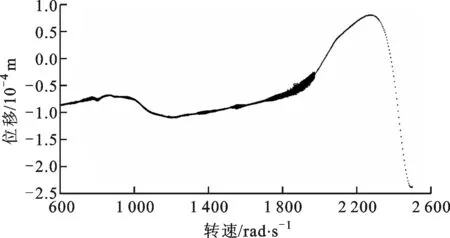
圖19 水平盤旋狀態下碰摩故障-帶SFD轉子系統分岔圖

在水平盤旋狀態下,對于碰摩故障-帶SFD轉子系統,系統盤集中質量節點在x方向上位移隨轉速變化的分岔圖如圖19所示。當轉速小于1 705 rad/s時,系統以周期1形式運動,在710～810、1 340～1 450、1 520～1 610 rad/s區間以擬周期運動;當轉速到1 705 rad/s,系統進入擬周期運動,當轉速大于1 980 rad/s時,系統以周期1運動,直到2 500 rad/s。

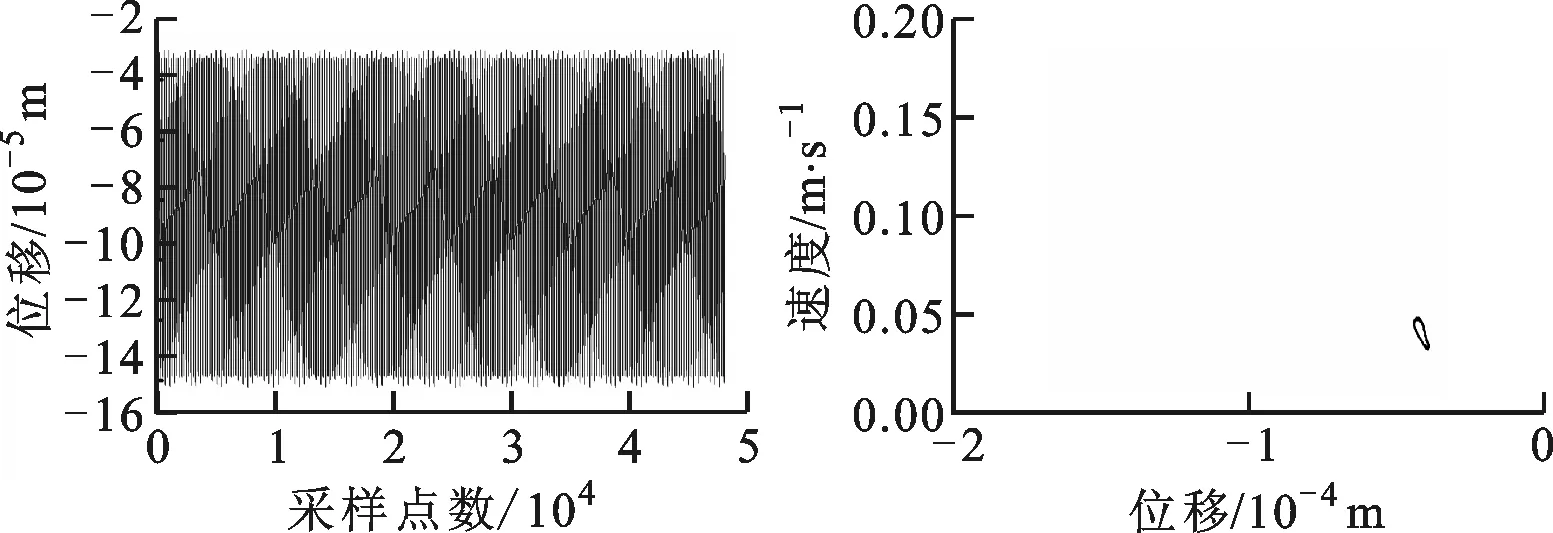
(a)時域圖 (b)龐加萊圖

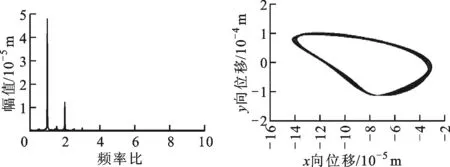
(c)頻譜圖 (d)軸心軌跡圖圖20 ω=1 400 rad/s時水平盤旋狀態下無SFD-碰摩故障轉子的系統圖

當轉速為1 400 rad/s時,由圖20可知,對于碰摩故障-無SFD轉子系統,系統以擬周期運動,系統出現了2倍頻分量和微小的分頻分量,軸心軌跡出現網狀結構和不規則形狀;由圖21可知,對于碰摩故障-帶SFD系統,轉子系統以周期1形式運動,系統無2倍頻和分頻量,同時軸心軌跡形狀規則,無網狀結構。

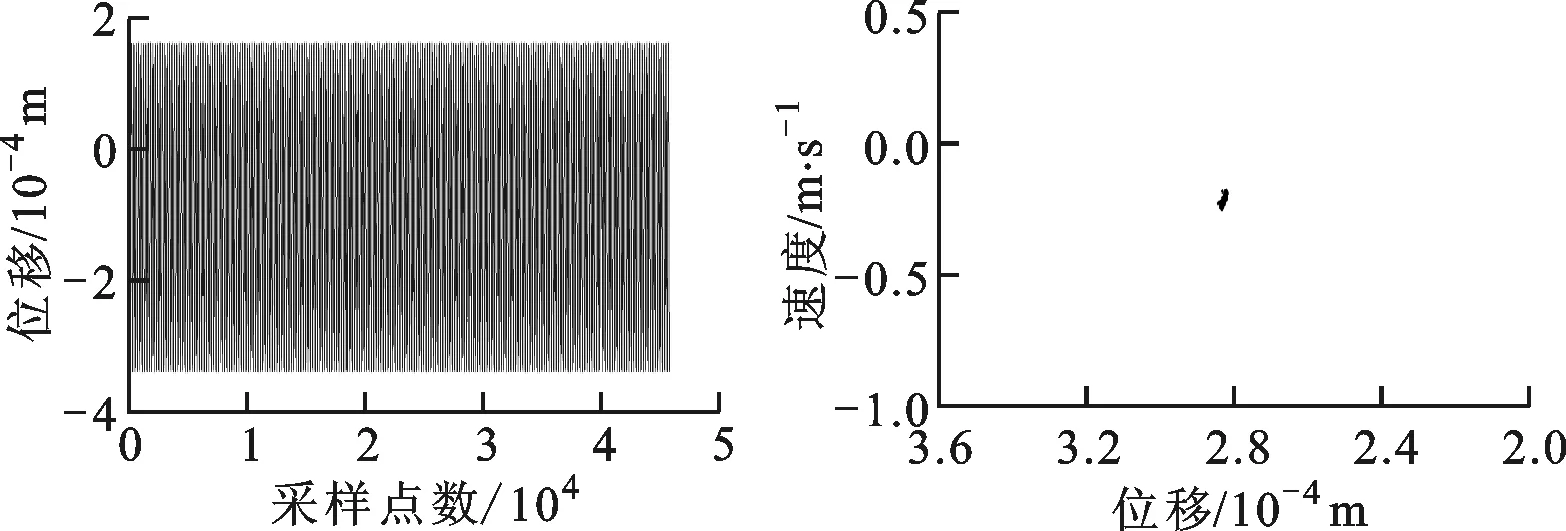
(a)時域圖 (b)龐加萊圖

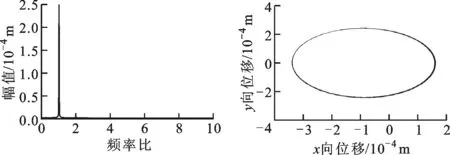
(c)頻譜圖 (d)軸心軌跡圖圖21 ω=1 400 rad/s時水平盤旋狀態下帶SFD-碰摩故障轉子的系統圖

由圖22可知,當轉速為2 000 rad/s時,對于碰摩故障-無SFD轉子系統,轉子系統以分岔形式運動,系統有微小的分頻量,轉子的軸心軌跡出現網狀結構;對于碰摩故障-帶SFD系統,由圖23可知,系統以周期1形式運動,系統分頻量消失,僅有微小的2倍頻分量,軸心軌跡形狀規則。通過對比可知,水平盤旋狀態下,SFD對于轉子系統的穩定性有著重要影響,在不同轉速下,轉子系統的運動軌跡相比于起飛、橫滾狀態有了較大的改變。

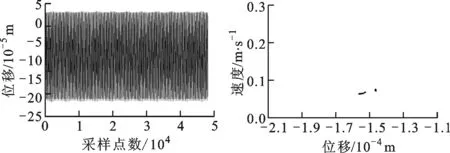
(a)時域圖 (b)龐加萊圖

(c)頻譜圖 (d)軸心軌跡圖圖22 ω=2 000 rad/s時水平盤旋狀態下無SFD-碰摩故障轉子的系統圖

(a)時域圖 (b)龐加萊圖

(c)頻譜圖 (d)軸心軌跡圖圖23 ω=2 000 rad/s時水平盤旋狀態下帶SFD-碰摩故障轉子的系統圖

3 結 論

本文基于Lagrange方程建立了飛機在空間進行機動飛行時發動機轉子系統的動力學模型,引入SFD并考慮轉靜碰摩故障,研究了不同機動飛行狀態下SFD對故障系統動力學性能的影響,得出如下結論。

(1)在文獻[11]的基礎上,考慮了SFD對系統的影響和碰摩故障,建立了機動飛行條件下轉子-SFD-碰摩故障的動力學模型,用龍格庫塔法進行求解,得到一定條件下起飛、橫滾、水平盤旋狀態時無SFD和帶SFD系統的動力學響應,通過對響應的分析發現,機動飛行狀態對轉子系統的動力學特性有著重要影響,對于不同參數機動飛行狀態下轉子系統性能的研究有重要的指導意義。

(2)通過對不同機動飛行狀態下無SFD與帶SFD的轉子碰摩故障轉子系統運動分岔圖的比較,發現在起飛、橫滾狀態下,帶SFD系統在高轉速下的系統穩定性有較大的提高,但是在中低轉速下系統穩定性反而有所降低;在水平盤旋狀態下,SFD系統在大部分轉速下系統的穩定性都有較大提高,并且SFD對于碰摩故障系統的動力學響應有較大的影響。因此,在不同狀態下,選擇合適的SFD參數對于提高系統的穩定性有重要的作用,這對于SFD的特性研究和性能優化有著一定的指導意義。

(3)通過對不同機動飛行條件無SFD和帶SFD碰摩故障轉子系統運動的時域圖、頻譜圖、龐加萊圖以及軸心軌跡圖的比較,發現不同機動飛行條件下其運動軌跡有著較大的差別,這對機動飛行狀態下故障轉子-滾動軸承-SFD系統的響應分析具有一定的指導意義。

[1] SIEW C C, HILL M, HOLMES R. Evaluation of various fluid-film models for use in the analysis of squeeze film dampers with a central groove [J]. Tribology International, 2002, 35(8): 533-547.

[2] 薛中擎, 孟光. 擠壓油膜阻尼器減振機理若干問題 [J]. 航空動力學報, 1988, 3(4): 309-314. XUE Zhongqing, MENG Guang. On damping mechanism of squeeze film [J]. Journal of Aerospace Power, 1988, 3(4): 309-314.

[3] 孟光, 薛中擎, 祝長生. 柔性轉子-非同心型擠壓油膜阻尼器系統的非協調響應分析 [J]. 航空動力學報, 1987, 2(2): 122-126. MENG Guang, XUE Zhongqing, ZHU Changsheng. Investigation on the non-synchronous responses of flexible rotor-uncentralized squeeze film damper bearing system [J]. Journal of Aerospace Power, 1987, 2(2): 122-126.

[4] MORARU L. Numerical predictions and measurements in the lubrication of aeronautical engine and transmission components [D]. Toledo, USA: University of Toledo, 2005.

[5] MORARU L, KEITH T G, DIMOFTE F, et al. Dynamic modeling of a dual clearance squeeze film damper: part I Test rig and dynamic model with one damper [J]. Tribology Transactions, 2003, 46(2): 170-178.

[6] ZHOU Hailun, LUO Guihuo, CHEN Guo. Analysis of the nonlinear dynamic response of a rotor supported on ball bearings with floating-ring squeeze film dampers [J]. Mechanism and Machine Theory, 2013, 59(1): 65-77.

[7] 祝長生, 陳擁軍. 機動飛行時航空發動機轉子系統的振動特性 [J]. 航空學報, 2006, 27(5): 835-841. ZHU Changsheng, CHEN Yongjun. Vibration characteristics of aeroengine’s rotor system during maneuvering flight [J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(5): 835-841.

[8] 祝長生, 陳擁軍. 機動飛行時發動機轉子系統動力學統一模型 [J]. 航空動力學報, 2009, 24(2): 371-377. ZHU Changsheng, CHEN Yongjun. General dynamic model of aeroengine’s rotor system during maneuvering flight [J]. Journal of Aerospace Power, 2009, 24(2): 371-377.

[9] 徐敏, 廖明夫, 劉啟洲. 機動飛行條件下雙盤懸臂轉子的振動特性 [J]. 航空動力學報, 2002, 17(1): 105-109. XU Min, LIAO Mingfu, LIU Qizhou. The vibration performance of the double disk cantilever rotor in flight mission [J]. Journal of Aerospace Power, 2002, 17(1): 105-109.

[10]徐敏. 機動飛行條件下帶擠壓油膜阻尼器轉子系統的振動特性研究 [D]. 西安: 西北工業大學, 2003.

[11]徐敏, 廖明夫. 機動飛行條件下帶擠壓油膜阻尼器的Jeffcott轉子的振動特性 [J]. 航空動力學報, 2003, 18(3): 394-401. XU Min, LIAO Mingfu. The vibration performance of the Jeffcott rotor system with SFD in maneuver filght [J]. Journal of Aerospace Power, 2003, 18(3): 394-401.

[12]袁惠群, 王正浩, 聞邦椿. 彈性機匣雙盤碰摩轉子系統的穩定性 [J]. 振動與沖擊, 2010, 29(8): 52-54. YUAN Huiqun, WANG Zhenghao, WEN Bangchun. Analysis on stability of dual-discs rub-impact rotor with consideration of casing elasticity [J]. Journal of Vibration and Shock, 2010, 29(8): 52-54.

[13]李朝峰, 李鶴, 馬輝, 等. 碰摩故障多自由度轉子-軸承系統周期運動穩定性研究 [J]. 機械工程學報, 2010, 46(11): 107-113. LI Chaofeng, LI He, MA Hui, et al. Bifurcation and stability of the flexible rotor-bearing system with rub-impact by a continuum model [J]. Journal of Mechanical Engineering, 2010, 46(11): 107-113.

[14]聞邦椿, 顧家柳, 夏松波, 等. 高等轉子動力學 [M]. 北京: 機械工業出版社, 2000.

[15]INAYAT-HUSSAIN J I, KANKI H, MUREITHI N W. On the bifurcations of a rigid rotor response in squeeze-film dampers [J]. Journal of Fluids and Structures, 2003, 17(3): 433-459

[16]INAYAT-HUSSAIN J I. Stability and bifurcation of a rigid rotor in cavitated squeeze-film dampers without centering springs [J]. Tribology International, 2001, 34(10): 689-702.

(編輯 趙煒)

Effect of Squeeze Film Damper on Rotor System with Rub-impact Fault under Maneuvering Flight Conditions

ZHANG Junhong1,2,MA Liang1,2,LU Xin1,WANG Jun2,LIN Jiewei3

(1. State Key Laboratory of Engine, Tianjin University, Tianjin 300072, China; 2. Ren’ai College, Tianjin University,Tianjin 300000, China; 3. Institute of Sound and Vibration Research, University of Southampton, Southampton SO17 1BJ, UK)

Aeroengine faults have crucial effect on the safety of aircraft flying. A model of aeroengine rotor system was presented by using the Lagrange equation during maneuvering flight, a model of rub-impact faults was built according to the Coulomb’s friction, and a model of squeeze film damper (SFD) was built according to the Reynolds equation. The dynamic responses of rotor-SFD-ball-bearing system during different maneuvering flights under rub-impact faults were studied. The system equations were numerically integrated to obtain the vibration responses by Runge-Kutta method. The Bifurcation diagrams of the rotor system with rub-impact faults in different maneuvering flights, as well as the time-domain diagram, Poincare map, spectrum diagram and orbit plot of rotor system under typical rotating speeds (1 400 rad/s, 2 000 rad/s), were obtained to analyze the dynamic characteristics. The results show that the stability of the rotor system can be improved by SFD at high speed, and the non-linear characteristics of the system are weakened, but SFD may reduce the stability at low speed. Suppression of the non-linear response of the system by SFD depends on maneuvering flight conditions.

rotor-ball bearing system; maneuvering flight; rub-impact fault; squeeze film damper

2015-05-15。

張俊紅(1962—),女,教授,博士生導師。

國家自然科學基金委員會與中國民用航空局聯合資助項目(U1233201)。

時間:2015-09-11

10.7652/xjtuxb201511011

TH133.3

A

0253-987X(2015)11-0062-09

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150911.1110.006.html