基于微分幾何和擴張狀態觀測器的勵磁控制

常鮮戎，張海生，崔趙俊

（華北電力大學電力工程系，保定 071003）

同步發電機勵磁控制系統是現代電力系統的重要組成部分，對整個電力系統的穩定性有著重要作用。從PID 控制、電力系統穩定器到線性最優勵磁控制，顯著提高了系統電壓和功角的穩定性。但設計所依據的是在電力系統某一特定狀態下近似線性化的數學模型，在系統遭受大干擾、偏離設計平衡點較遠時，控制效果就會減弱。近年來，非線性控制理論在電力系統得到大量研究[1-2]，很大程度上改善了系統大干擾的穩定性。但因電力系統模型及參數有不確定性，使得非線性勵磁控制器在實際應用中有一定誤差。

自抗擾控制技術[3]針對模型不精確和擾動等問題，提供一條新的解決思路。擴張狀態觀測器ESO（extended state observer）是其核心部分，在低階情況下能有效觀測系統的內外擾動，將此內外擾動的估計值補償到控制規律中，以實現非線性模型動態補償線性化[4]。文獻[5]根據非線性控制系統的微分幾何理論，提出非線性勵磁控制器NEC（nonlinear excitation control）。雖然這種NEC 可顯著改善電力系統的靜態和暫態穩定性，但在穩定機端電壓方面效果不是很理想[6]，而比例積分控制對機端電壓具有良好的控制效果。

輸出函數的選取會直接影響變換后的線性空間構成，從而影響控制器的最終控制效果[7-8]。文獻[9]將輸出函數選為發電機角速度的偏差，構造含有機端電壓偏差ΔUt的偽線性系統，將ΔUt引入反饋，提高了機端電壓的調節能力。變結構控制最大優點是滑動摸態對內部參數的變動和外部擾動作用具有不變性，或不靈敏性、自適應性[10]。

本文提出一種基于微分幾何和擴張狀態觀測器的非線性變結構勵磁控制。首先根據微分幾何理論進行坐標變換，然后構造二階的ESO 得到動態補償線性化的系統，利用變結構理論設計虛擬控制量，并引入基于機端電壓偏差的比例積分控制，從而實現非線性勵磁控制規律的設計。

1 數學模型

對于單機無窮大系統，當同步發電機采用靜止可控硅快速勵磁方式時，發電機勵磁控制系統數學模型可用非線性微分方程組描述為

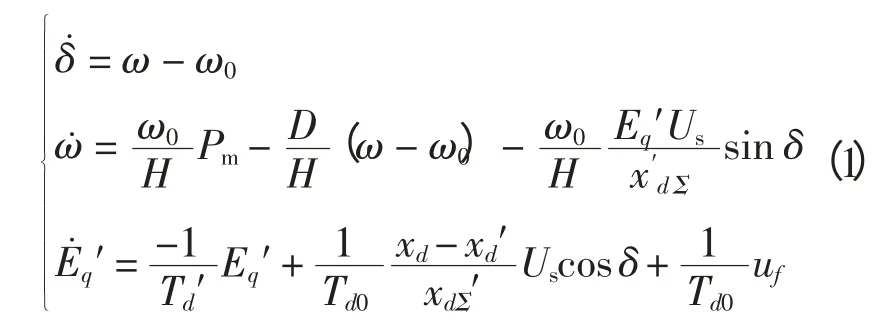
式中：δ 為發電機功角；ω 為角速度；Eq′為q 軸暫態電勢；H 為轉動慣量；xd和分別為發電機直軸同步電抗和暫態電抗；Td0為發電機定子開路時勵磁繞組時間常數；Td′為發電機定子閉路時勵磁繞組時間常數為阻尼系數；Pm為發電機機械功率；Us為無窮大系統母線電壓。

系統（1）化為仿射非線性系統，即

2 非線性勵磁控制規律的設計

2.1 坐標變換

考慮到轉速的變化超前于功角的變化和控制便于實現，同時也為了把輸出函數的穩態值選取在新坐標系的原點上，將輸出函數選為

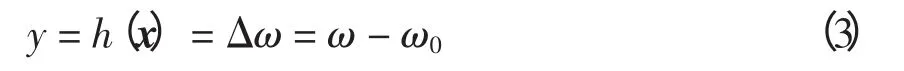
經計算可得：h（x）對系統的關系度為r=2。由于LgΔδ=0，故可選取以下坐標變換[11]，即

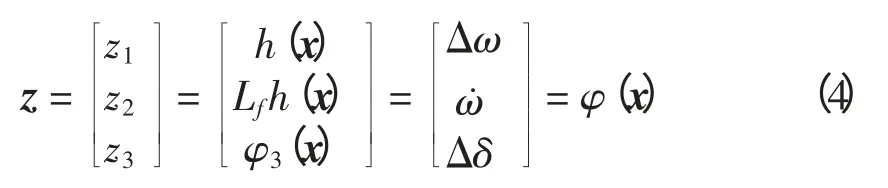
將式（1）變換成標準型方程為

根據微分幾何理論，得

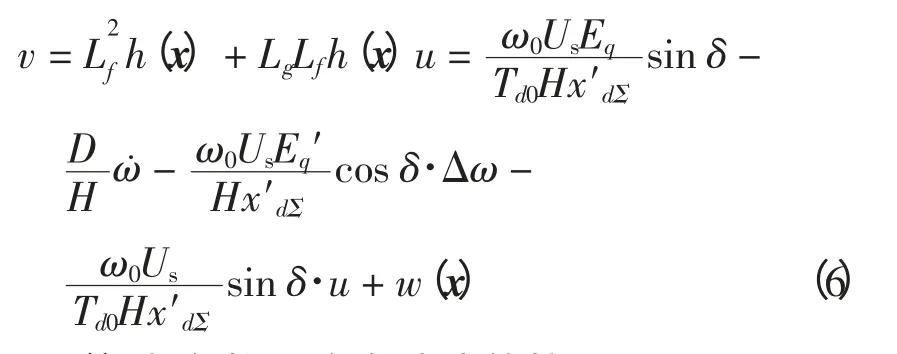
式中，w（x）為參數不確定造成的擾動。

可驗證，φ（x）的雅可比矩陣是非奇異的，即

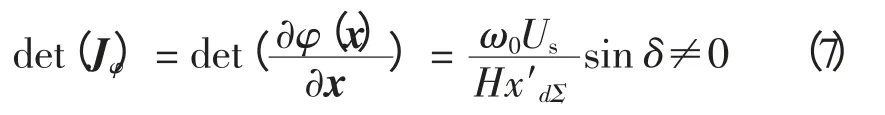
式（4）是狀態空間[Eq′，ω，δ]T與[z1，z2，z3]T之間的一個局部微分同胚。

2.2 擴張狀態觀測器

ESO 利用非線性函數來設計比系統多一維的狀態觀測器，從而估計對象的各階狀態變量，對不確定模型和擾動實時作用量補償。ESO 是動態過程，只需知道對象的輸入和輸出信息，對于系統構造ESO[4]為

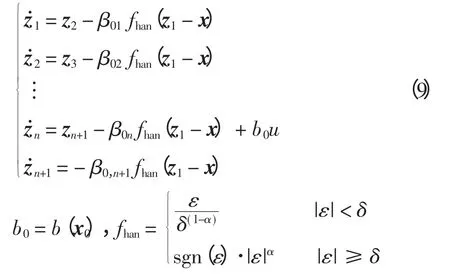
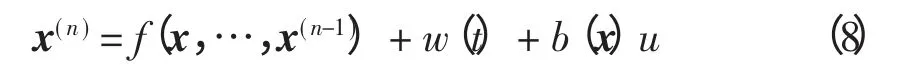
選擇合適的增益系數β01，β02，…，β0，n+1，使ESO更好地跟蹤系統的各個狀態：z1→x，z2→x˙，…，zn→x(n-1)，zn+1→f（x，…，x(n-1)）+w（t）。有了估計值zn+1，控制量可表示為

根據上述ESO 的動態反饋線性化理論，由于系統的非線性變量集中式（5）中的第2 個方程，觀測器的階數比對象高一階，故對式（5）中的第2 個方程構造相應的二階ESO。

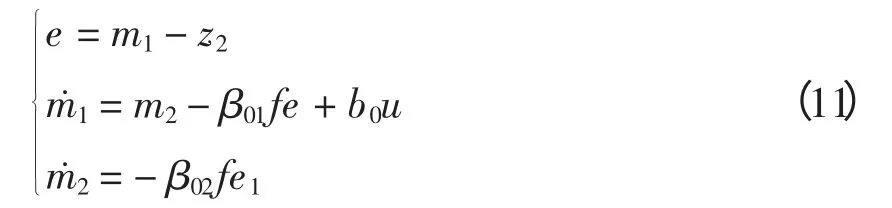
式中：m1為z2的估計值；m2為擴張變量，即

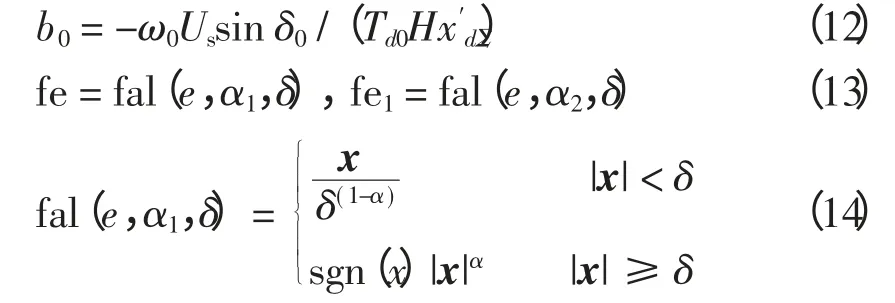
取控制量

2.3 變結構控制

變結構控制是一種控制系統的設計方法，可用于控制系統的跟蹤、調節、自適應和不確定等，適用于線性和非線性系統。

根據變結構控制理論，取切換函數為

式中，c1為常數。

為了使滑模控制具有良好的動態品質，選擇指數趨近律為

式中，ε、m 為正常數。

由式（5）、（16）、（17），可得

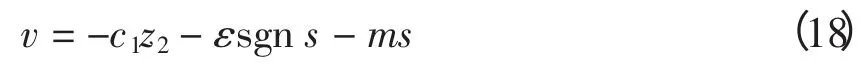
為了抑制滑模面上抖動，采用飽和函數代替式（18）的符號函數為

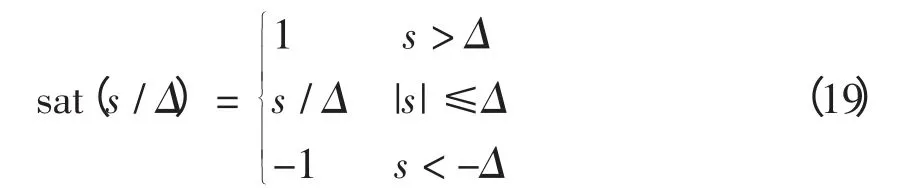
式（18）又可寫成為

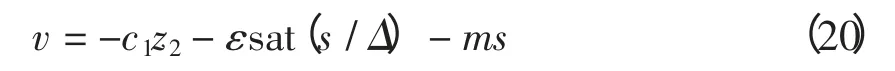
式（20）代入式（15），得非線性勵磁控制規律為

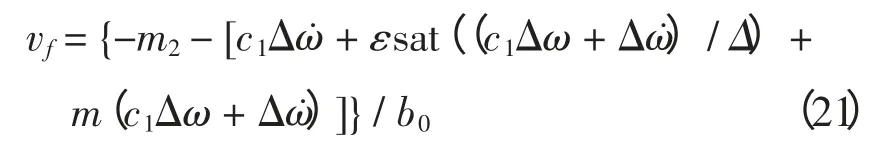
在式（21）的非線性勵磁控制規律中加入機端電壓偏差的比例積分控制，用以調節機端電壓，得到最終的勵磁控制規律為

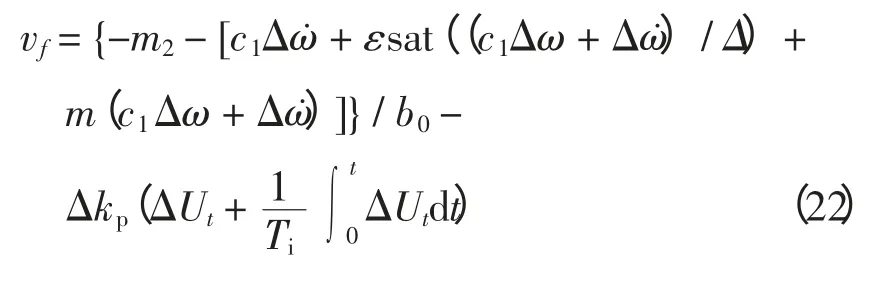
3 仿真分析

為論證本文所設計的非線性勵磁控制器具有較好的控制效果，與文獻[5]提出的非線性勵磁控制器比較，圖1 所示單機無窮大系統為例。

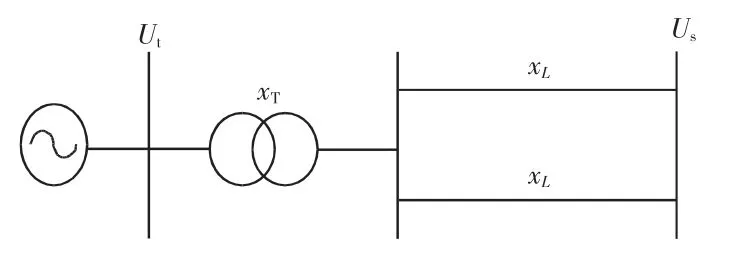
圖1 單機無窮大系統Fig.1 Single-generator infinite bus power system

仿真軟件采用Matlab。電力系統的模型參數為：xd= 1.0，xq= 0.6，xσ= 0.15，xd′ = 0.3，xd″ = 0.21，xq″=0.31，H=6 s，D=0.1，Td0=4 s，xT=0.088，xL=0.2。系統平衡點參數為：δ0= 22.15°，ω0= 1，Pe0=0.835，Qe0=0.26。設計的ESO 參數為：α1=0.5，α2=0.25，δ=0.01，β01=70，β02=10。設計變結構控制器參數為：c1=10，ε=0.1，m=10，Δ=0.1。PI 控制器參數為：kp=60，Ti=600。

3.1 機械功率擾動實驗

機械功率Pm在t=1 s 時發生20%的階躍擾動。機端電壓Ut、功角δ、有功功率Pe和角速度偏差量Δω 的動態響應曲線如圖2 所示。圖中，實線為本文提出的改善機端電壓的非線性勵磁控制，虛線為文獻[5]提出的非線性勵磁控制器。

圖2 表明，系統在小擾動情況下，常規非線性勵磁控制器使發電機機端電壓偏離擾動前的狀態，而本文設計的勵磁控制器使發電機機端電壓在擾動后基本恢復到擾動前的值，同時使系統在擾動結束后較快地穩定下來。

3.2 三相短路實驗

在t=1 s 時一回輸電線路首端發生三相短路，0.2 s 后故障切除，系統單回路供電。發電機機端電壓Ut、功角δ、有功功率Pe和角速度的偏差量Δω的動態響應曲線分別如圖3 所示。

從圖3 看出，本文設計的勵磁控制器在大擾動下，發電機機端電壓基本恢復到短路前的值，滿足電壓精度要求，同時系統功角和角速度進入穩態所需時間略短，對大干擾有一定的抑制作用。

3.3 參數擾動實驗

令參數Td0發生+50%擾動，從而引起b0值變化，通過觀察系統響應來驗證控制器的魯棒性。機端電壓Ut、功角δ、有功功率Pe和角速度偏差量Δω 的動態響應曲線如圖4 所示。由圖4 可看出，當參數發生擾動時，由于ESO 補償系統模型擾動，本文設計的勵磁控制器恢復到穩態的時間比常規非線性勵磁控制器要短，狀態響應產生的偏差也小，說明本文方法具有較好的魯棒性。

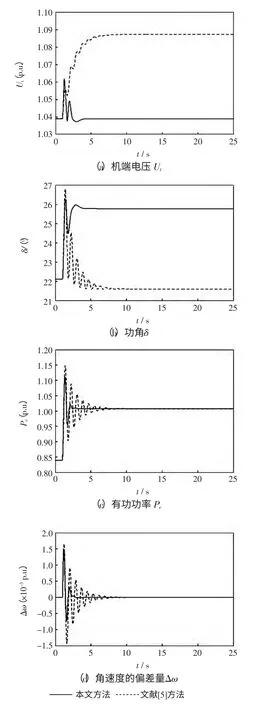
圖2 機械功率擾動實驗Fig.2 Mechanical power disturbance experiment

4 結語

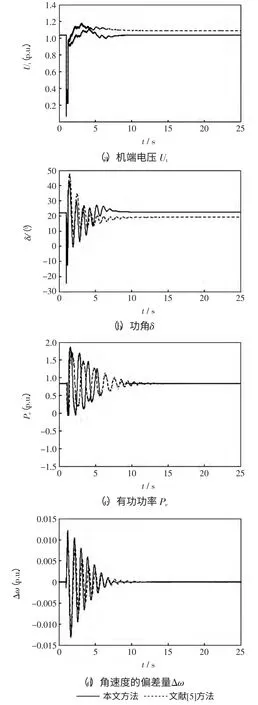
圖3 三相短路實驗Fig.3 Three-phase short circuit experiment

本文將微分幾何理論、ESO 理論和變結構控制理論相結合，提出了一種基于微分幾何和擴張狀態觀測器的非線性變結構勵磁控制。仿真結果表明，在機械功率擾動和三相短路故障下，所設計的勵磁控制器的控制效果優于常規非線性勵磁控制器，能改善機端電壓的調節精度，較好地保證發電機角速度、功角的穩定。同時，采用ESO 來估計未知參數和非線性模型，降低了控制器的復雜程度，對系統不確定性具有較好的魯棒性。

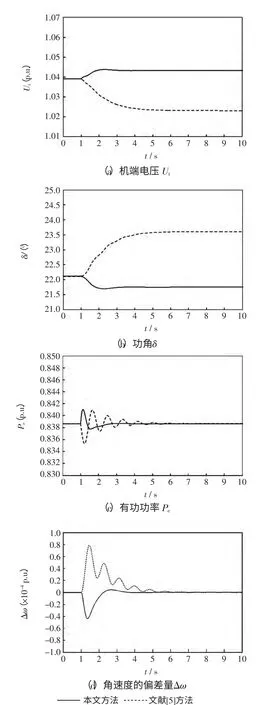
圖4 參數擾動實驗Fig.4 Parameter disturbance experiment

[1]萬黎，鄧長虹，陳允平（Wan Li，Deng Changhong，Chen Yunping）.考慮機端電壓限制的多重非線性變結構勵磁控制（Multi-layer nonlinear variable structure excitation control considering voltage limitation）[J]. 中國電機工程學報（Proceedings of the CSEE），2008，28（19）：86-92.

[2]王興貴，黃忠良（Wang Xinggui，Huang Zhongliang）. 同步發電機勵磁系統的智能變結構控制（Intelligent sliding mode variable structure control for synchronous generator excitation system）[J]. 電力系統及其自動化學報（Proceedings of the CSU-EPSA），2006，18（6）：79-82.

[3]韓京清（Han Jingqing）.從PID 技術到“自抗擾控制”技術（From PID technique to active disturbances rejection control technique）[J]. 控制工程（Control Engineering of China），2002，9（3）：13-18.

[4]韓京清.自抗擾控制技術[M].北京：科學出版社，1993.

[5]盧強，孫元章.電力系統非線性控制[M].北京：國防工業出版社，2008.

[6]孫元章，黎雄，戴和平，等（Sun Yuanzhang，Li Xiong，Dai Heping，et al）.同時改善穩定性和電壓精度的非線性勵磁控制器（A nonlinear excitation controller to improve both power system stability & voltage regulation accuracy）[J].中國電機工程學報（Proceedings of the CSEE），1996，l6（5）：332-336.

[7]李嘯驄，程時杰，韋化，等（Li Xiaocong，Cheng Shijie，Wei Hua，et al）.一種高性能的非線性勵磁控制（A high performance nonlinear excitation control for generator unit）[J].中國電機工程學報（Proceedings of the CSEE），2003，23（12）：37-42.

[8]李嘯驄，程時杰，韋化，等（Li Xiaocong，Cheng Shijie，Wei Hua，et al）.輸出函數在單輸入單輸出非線性控制系統設計中的重要作用（Important effection of the output function in SISO nonlinear control system design）[J].中國電機工程學報（Proceedings of the CSEE），2004，24（10）：50-56.

[9]陳鐵，舒乃秋（Chen Tie，Shu Naiqiu）.非線性勵磁控制方法的研究（Research of the nonlinear excitation based on the direct feedback linearization）[J]. 繼電器（Relay），2005，33（19）：28-30，35.

[10]王奔，毛宗源（Wang Ben，Mao Zongyuan）. 大型同步發電機變結構勵磁控制（Giant synchronous generationset′s Variable structure controller）[J].電力系統及其自動化學報（Proceedings o f the CSU-EPSA），1998，10（2）：1-6，14.

[11]胡躍明.非線性控制系統理論與應用[M].北京：國防工業出版社，2002.