UPFC 模糊控制器優化設計

侯 麗，劉 琦，魯寶春

（1.黃山學院信息工程學院，黃山245021；2.上海大學通信與信息工程學院，上海200444；3.遼寧工業大學光伏學院，錦州121001）

隨著現代電力互聯網絡的發展，提高現代電力系統的安全穩定性以及傳輸能力已成為電力研究者亟待解決的問題。統一潮流控制器（UPFC）是現代電力系統應用領域中功能最全面、特性最優越的柔性交流輸電裝置，既能通過快速地無功吞吐，動態地支撐UPFC 所接入點處的母線電壓，提高電力系統的電壓穩定性，又能靈活地調節輸電線路的潮流。PI 控制[1-3]因其設計簡單在UPFC 控制器設計中應用最為廣泛。但當運行工況發生改變時，PI 控制很難達到理想的控制效果。模糊控制技術因其對調節對象的參數具有較強的魯棒性而被應用于UPFC 控制器設計中[4-10]。

本文提出將模糊控制和遺傳算法相結合來設計UPFC 控制器。采用基于分層自適應遺傳算法搜索控制過程不同階段上UPFC 并聯側母線電壓模糊控制器、UPFC 直流側電容電壓模糊控制和UPFC 串聯側潮流模糊控制器的輸入誤差及誤差變化的量化因子、輸出比例因子的最優值，既保證了尋優中種群多樣性，又提高了遺傳算法的收斂速度。基于智能權函數法設計帶有自調整函數的模糊控制規則，以適應不同運行條件下的控制需求。

1 UPFC 控制器整體框架設計

采用二維模糊控制器結構來設計UPFC 控制器，其基本思想是利用反饋發現誤差，再利用誤差及誤差變化去消除誤差。UPFC 控制器整體框架設計如圖1 所示。首先，將系統的給定值R 與系統輸出值y 的誤差e（nT）（T 為采樣時間）以及誤差變化ec（nT）分別經過各自的輸入量化因子Ke、Kc和量化函數Qe、Qc，得到誤差的模糊量E（nT）以及誤差變化的模糊量EC（nT）（模糊化）作為模糊控制器的輸入變量。其次，基于智能權函數法設計自調整模糊控制規則，得到輸出控制量的模糊量U。然后，經過輸出比例因子Ku，轉化為輸出控制量u（去模糊化）去控制被控對象（線路潮流、節點電壓等）。此外，為了提高UPFC 模糊控制器在整個控制過程中不同階段的適應性，基于時間乘絕對誤差積分ITAE（integral time absolute error）準則確定系統參數優化的目標函數，采用分層自適應遺傳算法搜索輸入誤差量化因子Ke、輸入誤差變化的量化因子Kc和輸出比例因子Ku的最優值。

圖1 UPFC 控制器整體框架設計Fig.1 Overall framework design of UPFC fuzzy controller

2 模糊控制算法

在進行UPFC 模糊控制器設計時，兼顧提高靜態性能、動態性能、魯棒性能和算法本身的自優化能力，采用非均勻模糊量化策略和基于智能權函數法設計模糊控制規則。

2.1 非均勻模糊化與去模糊化

1）非均勻模糊化

非均勻模糊化是將誤差e（nT）與誤差變化ec（nT）的精確量變為誤差E（nT）和誤差變化EC（nT）的模糊量的過程。其表達式為

式中：Ke、Kc分別代表誤差及誤差變化的量化因子；Q（x）為量化函數[8]，其表達式為

式中，Lk（i），k 取1 或2 分別表示誤差E（nT）或誤差變化EC（nT）的模糊子集。借助Q（x）實現誤差及誤差變化的模糊論域劃分，兼顧提高系統的穩態精度和動態性能，采用零檔區間最小，隨著檔次增大，相應的區間依次增大的非均勻模糊化策略。

2）去模糊化

去模糊化是將經過模糊控制規則輸出的模糊控制量U 變為精確量u 的過程。其表達式為

式中，Ku代表輸出控制量的比例因子。

2.2 基于智能權函數的模糊控制規則

受自調整模糊控制規則[1]的啟發，當系統誤差（誤差變化）相對較大時，需要對誤差（誤差變化）控制作用給予較大的加權，加權大小與誤差（誤差變化）成正比。為了進一步改善模糊控制器的動態性能及魯棒性能，引入誤差及誤差變化本身的絕對值作為自身的加權值，將誤差的權函數αE和誤差變化的權函數αEC分別設計為

基于式（4）設計的智能權函數，分別對誤差及誤差變化兩個輸入變量進行加權，模糊控制規則設計為

式中：算子〈x〉表示取與x 同號且最接近于x 的整數；U 及U0分別代表模糊控制器的瞬態輸出及穩態輸出的模糊值。顯然，該種模糊控制規則的顯著特點是權函數僅僅是輸入變量（誤差及誤差變化的模糊量）的函數，且本身具有仿人智能的控制思想和優化特性，易于實時實現。

3 分層自適應遺傳算法

UPFC 模糊控制器控制性能的優劣與量化因子、比例因子的參數選擇密切相關，為了更好地適應電力系統不同階段控制特性的需求，采用分層自適應遺傳算法優化UPFC 所接母線電壓、被控線路潮流、及UPFC 直流電容電壓各自的輸入誤差量化因子Ke、輸入誤差變化的量化因子Kc和輸出比例因子Ku，克服了傳統遺傳算法在搜索后期效率低，易出現早熟和局部收斂，以及遺傳算子存在局限性[11]等缺點。其總體設計流程如圖2 所示。

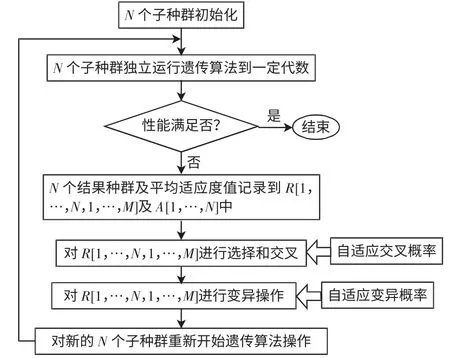
圖2 分層自適應遺傳算法流程Fig.2 Flow chart of hierarchical adaptive genetic algorithm

3.1 分層策略

對于待優化的參數，采用簡單易用的二進制編碼，基于人工經驗產生N×M 個個體的初始種群，然后把它們分成N 個子種群，每個子種群GAi（i=1，2，…，N）包含M 個個體，且獨立運行各自的遺傳算法。在每個GAi運行到一定代數后，用數組R[1，…，N，1，…，M]（R[i，j]代表GAi的第j 個個體）記錄N 個遺傳算法的結果，用數組A[1，…，N]（A[i]表示GAi的結果種群平均適應度值）記錄N 個結果種群的平均適應度值。

采用分層策略，可以獲得具有不同優良模式的新的個體，避免了傳統遺傳算法產生的局部收斂和早熟現象，并且可提高算法的收斂速度和結果精度。

3.2 自適應遺傳算子

對R[1，…，N，1，…，M]循環執行選擇、交叉、變異操作，直到得到滿意的結果為止。其中交叉概率φc和變異概率φm兩個參數的選取是影響遺傳算法性能優劣的關鍵因素，為了提高群體在整個進化過程不同階段的適應性，提出采用自適應的φc和φm，其基本思想是：對于適應度高于群體平均適應值的個體，給予較低的φc和φm，使該解得以保護進入下一代，反之，給予較高的φc和φm，使該解被淘汰。

1）選擇

基于A[1，…，N]對R[1，…，N，1，…，M]代表的結果種群進行選擇操作，使得平均適應度高的結果種群將被復制到下一代，平均適應度低的結果種群將被淘汰。

2）交叉

假設R[i，1，…，M]和R[j，1，…，M]被隨機匹配到一起，選擇在位置處進行交叉（1 ≤i，j ≤N；1 ≤x ≤M-1）則R[i，x+1，…，M]和R[j，x+1，…，M]相互交換相應的部分。實現了GAi和GAj中結果種群的n-x 個個體的交換。

為了提高算法的收斂性能，提出自適應選擇交叉概率φc，其值設計為

式中：fmax為群體中最大的適應度值；favg為每代群體的平均適應度值；f′為要交叉的兩個個體中較大的適應度值；φc1為設定的群體中低于平均適應度值的個體的交叉率，φc2為群體中最大適應度值的個體的交叉率，取φc1=0.9，φc2=0.6。

3）變異

以很小的變異概率將少量隨機生成的新個體替換R[1，…，N，1，…，M]中隨機抽取的個體，構成N 個新的種群，重新開始在新的種群中繼續各自的操作。

為了提高算法的搜索能力，提出自適應選擇變異概率φm，其值設計為

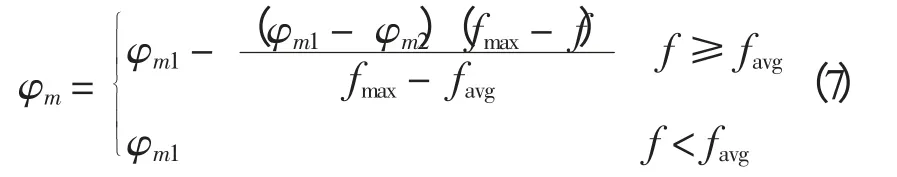
式中：f 為要變異個體的適應度值；φm1為設定的群體中低于平均適應度值的個體的變異率；φm2為群體中最大適應度值的個體的變異率，取φm1=0.1，φm2=0.001。

4 UPFC 各部分控制器優化設計

為了充分發揮UPFC 穩定節點電壓、調節線路潮流的作用，本文以保持UPFC 所接入處母線電壓US、UPFC 的直流電容電壓UDC分別為給定的參考值以及保持UPFC 所接線路的有功功率P、無功功率Q 分別為給定的參考值P*、Q*作為UPFC 的控制目標。基于該控制目標，通過控制UPFC 并聯側電壓源逆變器輸出交流電壓的縱分量Uid和橫分量Uiq分別控制UPFC 所接入處母線電壓US和UPFC 的直流電容電壓UDC，以及通過控制UPFC 串聯側電壓源逆變器輸出交流電壓的橫分量Ujq和縱分量Ujd分別控制線路的有功功率P和無功功率Q[9]。

為了綜合評價UPFC 控制器的動態及靜態性能，如響應速度快，調整時間短，超調小以及穩態誤差小等，基于ITAE（integral time absolute error）準則，選取優化的目標函數為

式中：tsim為仿真時間；ΔUS、ΔUDC、ΔIjd、ΔIjq分別為UPFC 并聯側電壓源逆變器所接母線電壓的誤差、UPFC 直流側電容電壓的誤差、UPFC 串聯側電壓源逆變器所接輸電線路電流縱分量的誤差、UPFC串聯側所接的線路電流橫分量的誤差。當目標函數最小時，控制器的調節性能最優。

基于式（8）的目標函數，采用分層自適應遺傳算法分別優化UPFC 并聯側母線電壓模糊控制器、UPFC 直流側電容電壓模糊控制器及UPFC 串聯側潮流模糊控制器的輸入誤差量化因子Ke、輸入誤差變化的量化因子Kc和輸出比例因子Ku，UPFC各部分控制器優化設計分別如圖3～圖6 所示。

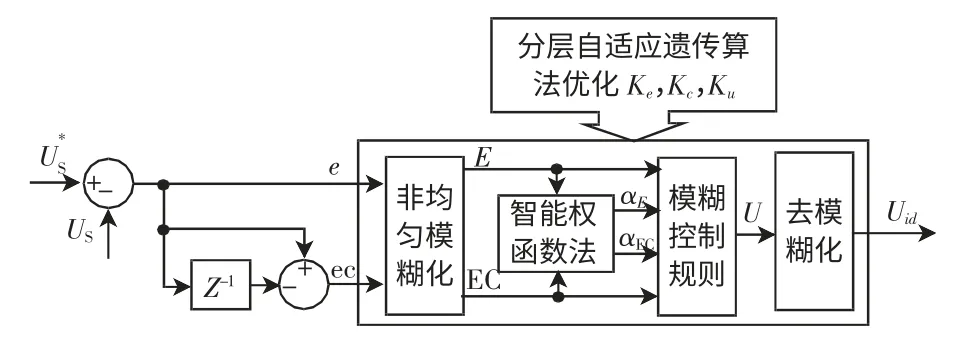
圖3 UPFC 并聯側母線電壓控制器Fig.3 Bus voltage controller at UPFC shunt side

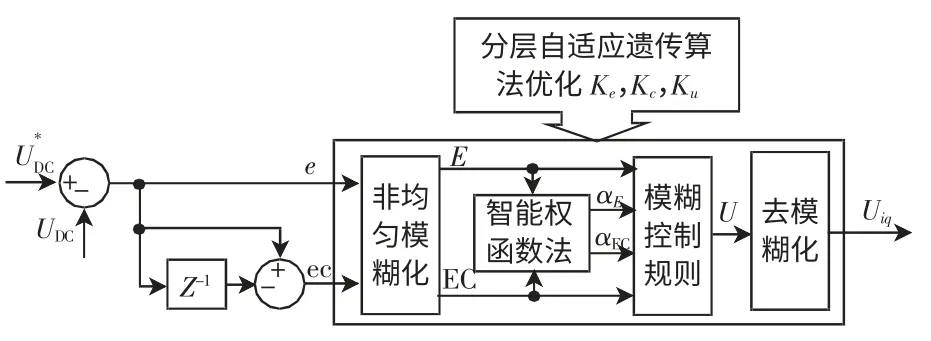
圖4 UPFC 直流側電容電壓控制器Fig.4 Capacitor voltage controller at UPFC DC side

圖5 UPFC 串聯側有功功率控制器Fig.5 Active power controller at UPFC series side

圖6 UPFC 串聯側無功功率控制器Fig.6 Reactive power controller at UPFC series side

5 仿真結果

設UPFC 安裝在單機無窮大系統的發電機出口升壓變壓器的高壓母線處，經雙回線與無窮大系統相連[12]。

仿真參數設置如下：發電機10.5 kV/500 MVA；頻率為fN=50 Hz；升壓變壓器為10.5 kV/242 kV；系統基準為220 kV，200 MWA；無窮大節點母線電壓US= 1 p.u.；UPFC 接入點母線電壓UAset= 1.1 p.u.；直流側電容電壓Udc=1 p.u.；線路潮流設定值為PLset=0.5 p.u.，QLset=0.3 p.u.；升壓變壓器參數為XT=0.1 p.u.；線路參數為RL=0.02 p.u.，XL=0.14 p.u.；并聯側變壓器參數為R1=0.05 p.u.，X1=0.2 p.u.；串聯側變壓器參數為R2=0.05 p.u.，X2=0.1 p.u.。

假設t=1.2 s 時，系統在雙回線的線路1 首端發生三相對稱短路，經過0.1 s 后故障切除，3 s 時PLset躍變到0.7，QLset躍變到0.5。UPFC 并聯側母線電壓UA、UPFC 直流側電容電壓Udc、UPFC 串聯側有功功率P 的仿真結果分別如圖7～圖10 所示。

圖7 UPFC 并聯側母線電壓仿真結果Fig.7 Simulation result of bus voltage at UPFC shunt side

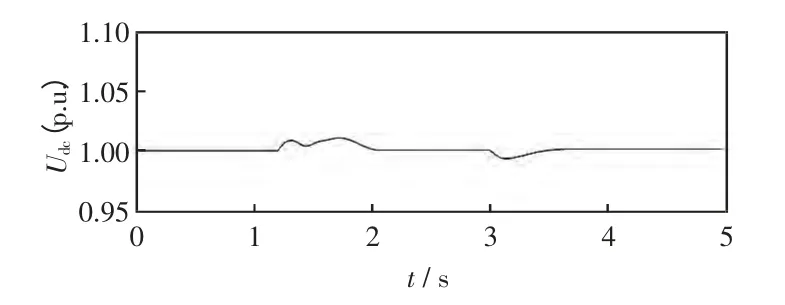
圖8 UPFC 直流側電容電壓仿真結果Fig.8 Simulation result of capacitor voltage at UPFC DC side

由圖7～圖10 的仿真結果可見：系統在1.2 s發生短路故障后，UPFC 所接入處的母線電壓和被控線路的潮流在0.5 s 內達到穩定值，UPFC 直流側電容電壓在暫態過程中電容電壓高于穩態值，隨著UPFC 的控制，在1 s 內恢復到初始設定的穩定值。

圖9 UPFC 串聯側有功功率仿真結果Fig.9 Simulation result of active power at UPFC series side

圖10 UPFC 串聯側無功功率仿真結果Fig.10 Simulation result of reactive power at UPFC series side

被控線路的潮流參考值在3 s 時發生躍變后，UPFC 所接入處的母線電壓和UPFC 直流側電容電壓均有所降低，通過UPFC 的控制很快達到穩定值，而被控線路的潮流能夠迅速跟上系統的設定值，穩態誤差很小，控制在0.3%以內。

6 結語

本文提出遺傳算法和模糊控制相結合進行UPFC 控制器設計，采用了非均勻模糊量化及基于智能權函數法的模糊控制規則來設計UPFC 模糊控制器，基于ITAE 準則作為系統優化的目標函數，通過自適應遺傳算法搜索UPFC 模糊控制器量化因子和比例因子的最優值。所設計的UPFC 控制器充分利用了遺傳算法的參數優化特性及模糊控制的魯棒性。相比傳統的PI 控制器，本文設計的UPFC 控制器能夠更加有效地調節UPFC 所接入處的母線電壓、維持UPFC 直流側電容電壓的穩定、控制輸電線路的潮流，并且具有響應速度快、控制精度高、魯棒性強的優良特性，更加有利于維持電力系統的安全、穩定運行，為UPFC 投入實際應用提供重要的參考價值。

[1]Gholipour E，Saadate S. Improving of transient stability of power systems using UPFC[J]. IEEE Trans on Power Delivery，2005，20（2）：1677-1682.

[2]Kannan S，Jayaram S，Salama M M A. Real and reactive power coordination for a unified power flow controller[J].IEEE Trans on Power Systems，2004，19（3）：1454-1461.

[3]Zangeneh A，Kazemi A，Hajatipour M，et al. A Lyapunov theory based UPFC controller for power flow control[J].International Journal of Electrical Power&Energy Systems，2009，31（7-8）：302-308.

[4]Elgamal M E，Lotfy A，Ali G E M.Voltage profile enhancement by fuzzy controlled MLI UPFC[J].International Journal of Electrical Power & Energy Systems，2012，34（1）：10-18.

[5]Ahmad S，Albatsh F M，Mekhilef S，et al.Fuzzy based controller for dynamic unified power flow controller to enhance power transfer capability[J].Energy Conversion and Management，2014，79：652-665.

[6]Routray S K，Nayak N，Rout P K. Design of a non-linear fuzzy controller based on differential evolution for UPFC control[J]. Journal of Bioinformatics and Intelligent Control，2013，2（4）：305-315.

[7]Linda M M，Pavithra S，Shiny N S.Unified power flow controller for stability enhancement of transmission system using intelligent control[J]. Artificial Intelligent Systems and Machine Learning，2014，6（3）：107-109.

[8]侯麗，劉琦，魯寶春（Hou Li，Liu Qi，Lu Baochun）.UPFC控制器設計（Controller design for UPFC）[J].電力自動化設備（ElectricPowerAutomationEquipment），2010，30（9）：51-54.

[9]侯麗，魯寶春（Hou Li，Lu Baochun）.一種新型的UPFC控制策略設計（A new control strategy design of unified power flow controller）[J].繼電器（Relay），2008，36（1）：33-36.

[10]楊偉，章慧蕓，仲海波（Yang Wei，Zhang Huiyun，Zhong Haibo）.基于模糊神經網絡的VSC-HVDC 系統控制器的研究（Research on controller of VSC-HVDC system based on fuzzy neural network）[J].電力系統保護與控制（Power System Protection and Control），2014，42（8）：115-120.

[11]韓民曉，馬杰，姚蜀軍，等（Han Minxiao，Ma Jie，Yao Shujun，et al）. 改進的遺傳算法辨識綜合負荷模型（Improved genetic algorithm and its application to composite load model）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2011，23（3）：79-83.

[12]顏偉，朱繼忠，孫洪波，等（Yan Wei，Zhu Jizhong，Sun Hongbo，et al）. UPFC 的模型與控制器研究（Study on model and controller of UPFC）[J].電力系統自動化（Automation of Electric Power Systems），1999，23（6）：36-41.