探測器薄壁箱體高低溫環境適應性分析

李金映，陳菊意，譚瑞軍，夏樹策，江　楠

(河南平原光電有限公司，河南 焦作 454001)

探測器薄壁箱體高低溫環境適應性分析

李金映，陳菊意，譚瑞軍，夏樹策，江楠

(河南平原光電有限公司，河南 焦作 454001)

摘要：在低溫和高溫的外界環境下，探測器薄壁箱體容易出現高低溫環境熱脹冷縮引起的無規則變形，這對內部光學元器件的光路傳遞精度造成影響，進而影響探測器的探測精度。應用有限元方法建立探測器箱體熱分析模型，運用ABAQUS軟件對薄壁箱體進行高低溫環境適應性分析，得到薄壁箱體在高低溫環境下的應力和變形，并計算探測器光軸兩端點之間因溫度變化引起的偏轉角度，在設計階段對探測器的溫度適應性能進行預測，減少設計人員以往基于經驗而非科學原理設計產品的盲目性，降低樣件試驗考核成本。

關鍵詞：薄壁箱體；環境適應性分析；有限元方法；變形

探測器是偵察設備的關鍵核心器件，其探測精度是制約探測器整體水平提高的重要因素。探測器的探測精度和結構可靠性受工況因素影響大。其中，熱環境對探測器箱體結構的變形影響較大，探測器在不同溫度下會產生熱脹冷縮變形，內部元器件可能產生位置偏移，又由于各個零部件材料、幾何特性不同，且存在相互作用，相同的溫度下各元器件因變形量不同而相互干涉影響偏移量。

箱體高低溫環境適應性對于提高探測器的探測精度有著重要作用。本文針對探測器薄壁箱體，建立了有限元熱環境計算模型，運用ABAQUS軟件求解，預定義溫度場加載進行熱應力分析，得到探測器箱體在一定溫度場下的應力云圖與位移云圖，并計算探測器光軸兩端點之間的偏轉角度，使得環境溫度引起的箱體變形不影響探測器的探測精度。

1熱分析有限元法的基本原理

運用有限元方法的熱分析原理將對象劃分成有限個單元，每個單元包含若干個節點，把在時間和空間連續分布的溫度離散分析為時間域、空間域有限個溫度值，然后根據能量守恒原理求解一定邊界和初始條件下每個節點處的熱平衡方程，通過求解若干個熱平衡方程得到各個節點的溫度值，并進一步求解出其他相關的物理量[1]。

1.1固體導熱微分方程

根據傅里葉傳熱定律和能量守恒定律，可以建立傳熱問題的控制方程，即物體的瞬態溫度場T(x,y,z,t)應滿足如下方程[2]：

(1)

式中，T是物體的溫度場；c是熱源強度系數；ρ是材料密度；CT是材料比熱；kx、ky、kz分別是沿x、y、z方向的傳熱系數；Q是物體內部熱源強度。

1.2初始條件和邊界條件

1.2.1初始條件

在分析瞬態問題時，需要定義初始條件，即要給出物體在初始時刻的溫度分布情況，其表達式為[3]：

T=f(x,y,z,t)

(2)

若初始時刻物體各處的溫度都相同，則初始條件為：

T=T0

(3)

1.2.2邊界條件

物體間進行熱交換的規律，邊界條件一般分為三類[4]。

第1類：溫度邊界條件。若在物體邊界Γ1上，任意一點處各個時刻的溫度函數已知，則這樣的邊界條件稱為第1類邊界條件，即：

T|Γ1=f(x,y,z,t)

(4)

T|Γ1=Ta

(5)

第2類：熱流密度邊界條件。若在物體邊界Γ2上，任意一點處各個時刻流入和流出物體表面的熱流密度為已知函數，這樣的邊界條件稱為第2類邊界條件，即：

(6)

式中，k是物質的傳熱系數；n是物體表面的法線方向。

(7)

式中，q是熱流密度。

若邊界Γ2為絕熱邊界，則邊界條件為：

(8)

第3類：對流邊界條件。若在物體邊界Γ3上，有熱對流發生，且函數關系已知，則稱為第3類邊界條件。對流邊界條件用公式表示為：

(9)

式中，α是物體與介質之間的換熱系數；Tf是流體介質的溫度。

2探測器箱體熱分析有限元建模

2.1薄壁箱體結構模型

某探測器箱體的結構簡化模型如圖1所示。為接近該探測器實際模型，保證計算的準確性，將該探測器的物鏡模型與箱體本體裝配，箱體各處的蓋(包括目鏡組件蓋、觀察窗組件蓋、左側面板組件蓋和轉換本體蓋)都與本體裝配進行熱應力分析。為減少計算規模，簡化略去了箱體蓋上的非承載結構。具體修改原則如下[5]。

圖1　簡化后箱體模型

1)探測器箱體本體與箱體蓋剛性連接，不考慮接觸面的相對變形，即整個箱體作為一個整體進行分析。

2)忽略箱體蓋上部分受載很小或影響甚微的局部結構，如手柄、旋鈕和某些凸臺。

3)調整細小的面、線的最小網格尺寸或單元數目，以適應有限元網格的劃分條件，避免局部網格過密。

2.2薄壁箱體有限元網格劃分

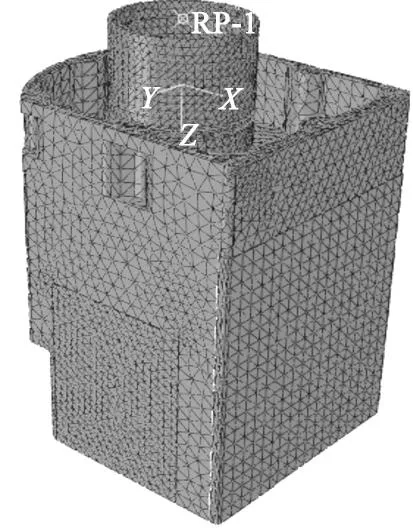
圖2　箱體的有限元網格模型

ABAQUS提供了龐大的單元庫，為用戶提供了一套強有力的工具以解決多種不同類型的問題。在實際工程問題中，像箱體這樣具有復雜結構形體，且有多處圓弧邊界，必須按照空間問題求解。空間問題節點自由度多，需要分割的單元數量多，因此計算量較大。在空間問題中對計算對象邊界擬合的能力較強的是四面體單元，因此這里選擇四面體單元C3D10進行網格劃分。C3D10是一種10節點二次實體單元，分析精度較高。

對模型進行多次不同精度和尺寸的自由網格劃分，綜合考慮網格的疏密、單元數目多少以及網格的質量、計算機的硬件配置和計算所需時間，最終確定箱體的網格模型(見圖2)，單元數目為102 203，節點數為178 084。

2.3材料屬性的定義

箱體本體材料為ZM5鑄鎂合金，物鏡框材料為鈦合金TC4，轉換本體材料為ZL101A，箱體蓋材料為MB8。查得4種材料參數[6]見表1。

表1　4種材料參數

2.4熱環境參數

系統工作狀態下存在的熱源來自2個方面：1)外部的溫度；2)內部各模塊發熱產生的熱量。探測器內部元器件無熱源，箱體外表面與空氣環境存在對流，箱體封閉導致內部無空氣對流，并且在溫度達到一定值(-40或50 ℃)保溫2 h后，整個探測器溫度基本與環境溫度相當，于是在ABAQUS軟件中運用預定義溫度場加載進行熱應力分析，初始溫度場設定為室溫(20 ℃)，模型最終溫度設定為-40~50 ℃，并每間隔10 ℃對狀態進行分析。

3薄壁箱體熱分析

在ABAQUS軟件中選擇默認參數設置[7]，進入load模塊，使用預定義場(Predefined Field)來定義初始溫度場20 ℃和最終溫度場分別為低溫-40 ℃、高溫50 ℃。進行熱分析后得到環境溫度分別為-40和50 ℃下的薄壁箱體應力云圖和位移云圖，分別如圖3和圖4所示。

a)應力云圖

b)位移云圖圖3　-40 ℃時的應力云圖和位移云圖

a)應力云圖

b)位移云圖圖4　50 ℃時的應力云圖和位移云圖

從分析結果的應力和位移云圖中可以看出：環境溫度為-40 ℃的情況下的最大Mises應力為425 MPa，最大位移為0.426 mm；環境溫度為50 ℃的情況下的最大Mises應力為212 MPa，最大位移為0.212 mm。同時，可以看出探測器結構對低溫環境的敏感性較強，因此，在探測器的結構設計時，更應該注意低溫環境下的應力和變形。

4探測器箱體光路誤差對溫度敏感性分析

為了研究探測器物鏡和目鏡之間光路誤差對環境溫度的敏感性，需要觀察物鏡中心點與轉向組件中心點之間的相對位置變化(見圖5)，因此可以在熱環境分析步的歷史變量輸出管理中設置輸出兩個觀察點的位移[8]。物鏡觀察點C位移隨溫度變化關系如圖6所示，轉向組件觀察點D位移隨溫度變化關系如圖7所示。

圖5　探測器有限元兩觀察點示意圖

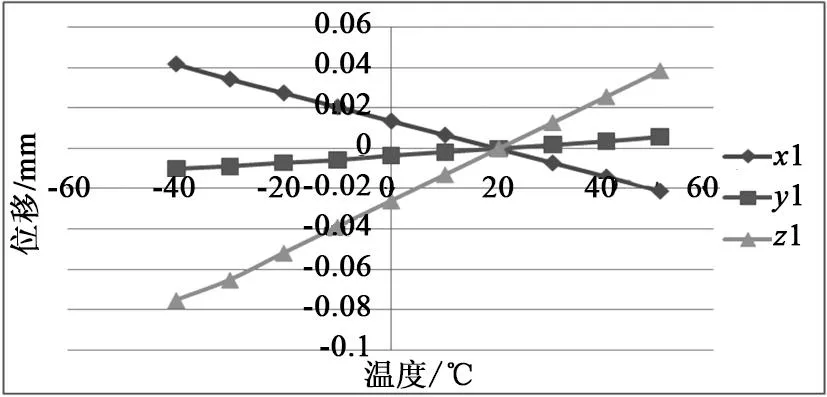
圖6　物鏡觀察點C位移隨溫度變化關系

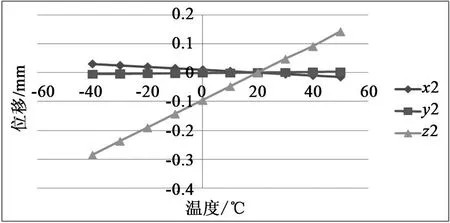
圖7　轉向組件觀察點D位移隨溫度變化關系

輸出不同溫度時，兩觀察點的位移見表2。根據表2的數據，繪制兩觀察點之間在3個坐標方向的坐標之差的絕對值曲線(見圖8)。

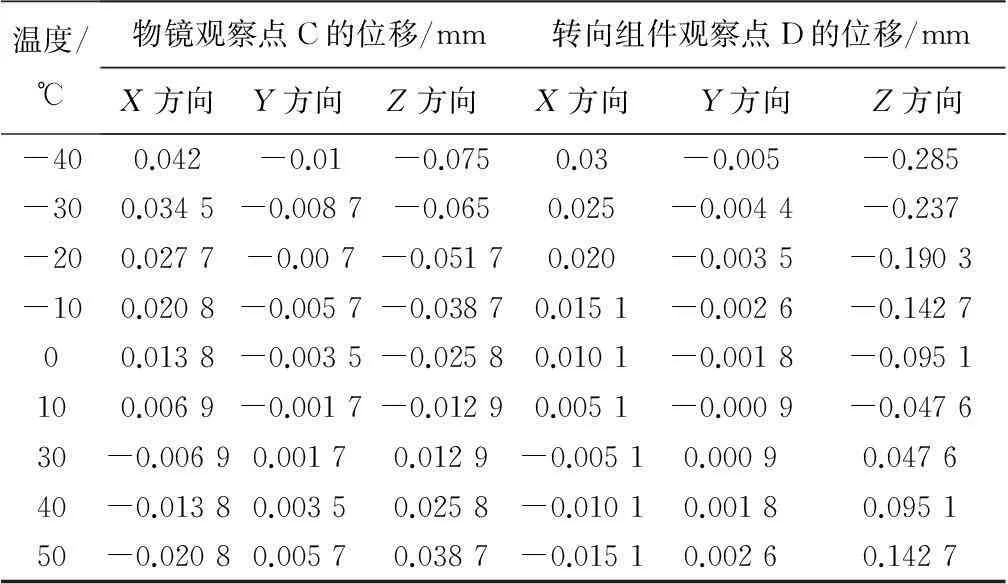
表2　觀察點不同溫度下的位移

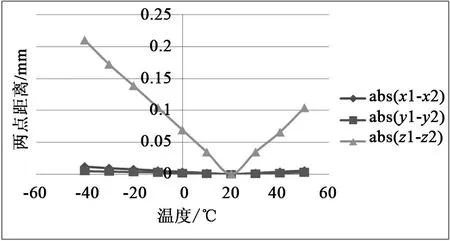
圖8　2個觀察點之間的距離

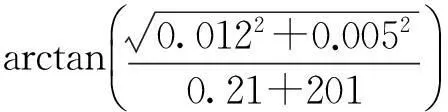
5結語

通過上述分析，可以得到如下結論。

1)采用ABAQUS軟件對探測器薄壁箱體進行環境熱分析，得到箱體結構在低溫-40 ℃和高溫50 ℃環境下的應力和位移云圖，可在設計階段實現對箱體高低溫環境適應性能的預測，代替樣件試驗從而縮短產品研制周期。

2)經過高低溫環境有限元熱分析，發現探測器箱體在低溫-40 ℃的環境下應力和變形更大，因此，在設計時更應該注意箱體在低溫環境下的變形問題。

3)以觀察鏡光軸兩端點在極端溫度環境下的相對偏轉角度作為判定設備高低溫環境適應性能的依據，進行設備的溫度環境適應性能分析，能夠有效保證設備的探測性能。

參考文獻

[1] 楊淇帆,梁睿君,葉文華.基于有限元的機床主軸箱部件的熱特性分析[J].機械科學與技術,2012(11):1860-1863，1867.

[2] 孔詳謙.有限單元法在傳熱學中的應用[M].北京:科學出版社,1986.

[3] 郭曉明.1.5MW風電增速箱箱體結構及熱分析[D].西安：西安理工大學，2010.

[4] 梅益,王方平,劉喬英.重載減速箱有限元熱-結構耦合分析研究[J].煤礦機械, 2011(8):58-60.

[5] 楊張小蟬.風電齒輪箱體熱結構特性分析研究[D].大連：大連理工大學，2009.

[6] 中國航空材料手冊編輯委員會. 中國航空材料手冊(第3、4卷)[M]. 北京：中國標準出版社，1988.

[7] 石亦平，周玉蓉. ABAQUS有限元分析實例詳解[M]. 北京：機械工業出版社，2010.

[8] 莊茁，由小川，廖建暉，等. 基于ABAQUS的有限元分析和應用[M]. 北京：清華大學出版社，2009.

責任編輯鄭練

Adaptability Analysis of Detector Thin-walled Box Worked in High and Low Temperature Environment

LI Jinying, CHEN Juyi, TAN Ruijun, XIA Shuce, JIANG Nan

(Henan Pingyuan Photoelectric Co., Ltd., Jiaozuo 454001, China)

Abstract:Thin-walled box appears irregular deformation caused by thermal expansion and contraction when working in the low and high ambient. This affects optical path passing accuracy of the internal optical components, and thereby affecting the accuracy of the detector. Thermal analysis model of detector thin-walled box is established by finite element method. High and low temperature environmental adaptability of thin-wall box is analyzed by ABAQUS software to get stress and deformation under high and low temperature environment. The deflection angle between two endpoints in the optical axis of the detector due to temperature changes is calculated. Detector temperature adaptability is forecasted in the design stage, and it can reduce the blindness of designers designing products and the cost of sample test assessment.

Key words:thin-walled box, adaptability analysis, FEM, deformation

收稿日期：2014-11-24

作者簡介：李金映(1977-)，男，高級工程師，主要從事光電系統總體技術設計等方面的研究。

中圖分類號：TH 136

文獻標志碼：A